2. 中国石油长庆油田分公司第五采油厂, 西安 710200;
3. 中国石油长庆油田分公司第八采油厂, 西安 710021
2. No.5 Oil Production Plant, Changqing Oilfield Company, PetroChina, Xi'an 710200, China;
3. No.8 Oil Production Plant, Changqing Oilfield Company, PetroChina, Xi'an 710021, China
0 引言
基于数字岩心技术的岩石物理数值模拟已经成为岩石物理研究的重要手段之一。数字岩心模型作为数字岩心技术的基础,国内外学者进行了广泛的研究,提出了多种建模方法[1-2]。数字岩心建模较多集中于对岩心孔隙结构的构建[3-7],由于岩心孔隙尺寸分布跨度大,可以从纳米级到毫米级,单一分辨率的数字岩心模型无法完整描述岩心孔隙特征。X射线计算机断层扫描(CT)是目前数字岩心建模应用最广泛的技术之一,但存在视场与分辨率之间的矛盾。分辨率较低时,可以获得较大的岩心尺寸,但同时丢失了微观结构信息;分辨率较高时,岩心微观特征更详细,但可能存在无法获得代表性体积元[8-9]的问题。因此,需要综合多种尺度的信息对岩心结构进行描述。Sok等[10]结合CT、背散射扫描电镜(BSEM)、聚焦离子束扫描电镜(FIB-SEM)等多种技术对碳酸盐岩进行了多分辨率成像,对孔隙分布进行了全尺度分析。Khalili等[11-12]对碳酸盐岩进行了多尺度成像,并进行了物理属性的升尺度模拟。王晨晨等[13]利用图像叠加的方法构建了双孔隙的碳酸盐岩数字岩心模型,但是该模型并非严格意义上的多尺度。白斌等[14]对致密砂岩样品进行了纳米-微米多尺度CT成像及孔隙表征,但没有涉及两种尺度模型的融合。
在数字岩心电性模拟与声学模拟中,除了孔隙结构外,构成岩石骨架的泥质、胶结物、矿物等含量及分布对模拟结果会产生影响[15],对于矿物组成复杂的页岩影响更大[16]。如果考虑矿物组分润湿性,润湿性的变化对渗流模拟也会产生影响。因此,数字岩心模型在刻画孔隙结构的同时,需要考虑岩心骨架的组分构成,尽可能全面、准确地描述岩心样品。
本文利用图像配准方法将不同分辨率下的岩心扫描图像进行空间配准,按照分辨率从高到低的顺序进行孔隙分割及骨架矿物分割,构建多尺度、多组分的数字岩心模型。
1 多分辨率岩心成像目前岩心成像方法主要包括X射线CT、扫描电镜(SEM)、FIB-SEM。其中X射线CT与FIB-EM属于三维成像,SEM为二维成像。微米CT最高分辨率可达亚微米级,SEM、FIB-SEM最高分辨率到几个纳米。本文以某砂岩样品为例,分别进行了两种分辨率的CT和FIB-SEM成像,并进行了扫描电镜矿物定量分析。
多分辨率岩心成像按照样品尺寸从大到小的原则,首先制备直径为1 in(2.54 cm)的岩心柱塞样品,利用微米CT设备进行成像实验,使用Xradia MicroXCT-200型扫描仪,所选样品长度为41.8 mm,样品气测孔隙度为10.61%,气测渗透率为4.32 mD①。图 1a为砂岩柱塞样品扫描二维切片,图像分辨率为27 μm。柱塞岩心成像可以反映岩心大尺度的结构特征(裂缝、大孔隙、夹层等),由于分辨率较低,大部分的微孔隙无法识别。因此通过柱塞样品成像观察孔喉发育情况,在柱塞样品上选取合适的位置钻取一个或多个子样品进行高分辨率扫描。子样品直径一般为2~10 mm。此次在柱塞岩心顶部中心位置钻取一个子样品,直径为6 mm,长度为1.1 cm。图 1b是柱塞岩心子样品成像的二维切片,分辨率为2.69 μm。在高分辨率扫描图像上,岩心大部分孔隙都可以准确识别出来,同时不同矿物颗粒的边界也更加明显。

|
| a.27 μm分辨率CT切片;b.2.69 μm分辨率CT切片;c.7 nm分辨率FIB-SEM成像切片。 图 1 砂岩样品不同分辨率岩心成像二维切片 Figure 1 Cross sections of sandstone sample at different resolutions |
|
|
① 毫达西(mD)为非法定计量单位,1 mD=0.987×10-3 μm2,下同。
岩心孔隙尺寸变化范围较大,对于非常规储层岩心,如致密砂岩、泥页岩等,纳米级孔喉较发育[17-18]。SEM仅限于二维成像,无法观察岩心三维结构特征。FIB-SEM将SEM与FIB聚焦离子束结合,利用Ga离子束对样品进行连续剥蚀,同时在电子束下成像,不仅获得了较高的分辨率,也真实地还原了岩心三维结构特征[19]。图 1c是在柱塞样品中选择某区域进行FIB-SEM成像的一个切片,成像视野为15 μm×11 μm,分辨率为7 nm。可以看到,在纳米尺度下,依然有少量孔隙存在。
数字岩心模型需要能够准确地反映岩石孔隙结构特征。通过不同分辨率的岩心扫描图像可以看出,低分辨率的岩心图像能够识别出较大的孔隙,尺寸小于扫描分辨率的微孔隙则无法有效识别[10]。高分辨率图像对应的岩心实际尺寸较小,相应的数字岩心模型难以确保具有代表性。基于扫描样品取样的继承性,可以将两种分辨率扫描图像进行空间上的配准,找到子样品图像在柱塞样品图像中的对应位置,形成多尺度岩心扫描图像。
2 多分辨率图像配准图像配准的实质是通过一系列空间变换操作,使得两幅图像间的对应点达到空间位置上的一致。图像配准的两幅图像,其中一幅为参考图像,另一幅为待配准图像。图像配准方法根据图像信息的利用情况可以分为基于灰度和基于特征两种。Latham等[20]提出基于灰度的岩心图像配准方法并进行了应用。在实际配准过程中,基于灰度的配准方法计算量较大,需要待配准图像的重叠区域占较大的比例。对于柱塞样品与子样品图像配准,在无法获知大致取样位置的前提下,很难得到正确的配准结果。
基于特征的图像配准方法通过图像的特征点来实现图像配准,与基于灰度的配准方法相比具有计算量小、抗噪声、对位置变化敏感、对灰度变换和图像形变有较好适应能力等优点。基于特征的图像配准方法一般分为5个步骤:特征提取、特征匹配、估计变换模型参数、图像插值和几何变换。
本文采用基于特征的图像配准方法中应用最广的SIFT(scale invariant feature transform)算法进行岩心图像的配准。SIFT算法由Lowe[21]于2004年提出,基于尺度空间,对图像平移、旋转、缩放、甚至仿射变换均保持不变性。
以二维图像配准为例,SIFT算法提取特征点包括4个步骤:
1) 建立高斯差分尺度空间
为了使特征具有尺度不变性,特征点的检测是在尺度空间完成的。大尺度对应于图像的粗略特征,小尺度对应于图像的细节特征。Koendetink等[22]证明了高斯卷积核是实现尺度变换的唯一变换核,所以一幅二维图像I(x, y)的尺度空间L(x, y, σ)定义为
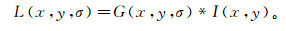 (1)
(1) 其中,
 (2)
(2) 式中:*表示卷积;G(x, y, σ)为尺度可变的二维高斯函数;(x, y)为图像的像素位置;σ为尺度空间因子,值越小表示图像被平滑得越少,相应的尺度也就越小。
在此基础上,通过相邻尺度空间两两相减获得高斯差分(DOG)尺度空间,高斯差分响应值D(x, y, σ)表达式为
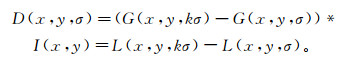 (3)
(3) 式中,k是表示两尺度空间倍数的常数。
2) 确定关键点
为了寻找尺度空间的极值点,每一个采样点均需要与自身及相邻尺度空间的邻域点进行比较。也就是在以采样点为中心的3×3×3立方体内,与其同尺度和上下相邻尺度的26个相邻点比较求极值,以确保在尺度空间和二维图像空间都是理想的极值点。删除低对比度的极值点和不稳定的边缘响应点。
3) 确定关键点的大小和方向
利用特征点邻域像素的梯度方向分布特性为每个特征点指定方向参数,从而使算子具备旋转不变性。对于尺度空间L(x, y, σ)中的任意一点,其梯度幅值m(x, y)和方向θ(x, y)可表示为
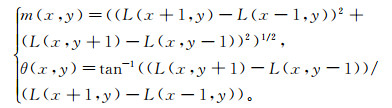 (4)
(4) 4) 提取特征描述符
将坐标轴旋转为与关键点方向一致,以关键点为中心取16×16的窗口,分成16个4×4的子块,在每个子块上计算8个方向的梯度直方图,得到一个具有8个方向的种子点。每个关键点可以用4×4个种子点描述,组成一个128维的特征向量,即128维描述符。
提取特征点后,进行特征点的匹配。这里以欧氏距离作为相似性度量函数,其定义为
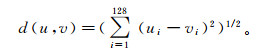 (5)
(5) 式中:u和v为任意的两个关键点;ui和vi为各自的第i个分量。当u和v互为匹配点时,d(u, v)值最小。特征点匹配过程如下:
① 在参考图像中选取一个极值点作为参考点,在待配准图像中选出满足与参考点欧氏距离最短的两个点;
② 以两个欧氏距离中小的值做分子,大的值做分母,如果该分数值在给定的某阈值范围内,则接受距离最近的点作为匹配点,更换参考点返回①;
③ 不满足上述条件,寻找距离最短的第三个点,返回②;
④ 循环超过某设定次数,放弃参考点,更换参考点返回①。
根据匹配的特征点确定变换矩阵,对参考图像进行相应的空间变换。相同分辨率岩心图像的变换为刚体变换,不同分辨率图像的变换为仿射变换。对变换图像重新插值,最终得到完全匹配的两幅图像。
利用SIFT算法进行子样品与柱塞样品的图像配准,在柱塞样品图像中得到与子样品图像对应的低分辨率配准图像。图 2所示为与图 1b相对应的低分辨率图像,圆圈表示子样品的钻取位置。图 3显示了完成配准的子样品与柱塞样品在三维空间中的叠加。其中,长方体为低分辨率的柱塞岩心,半圆柱体为高分辨率的子样品。由于子样品只占柱塞样品体积的一部分,通过图像配准之后,岩心子样品同时具有27 μm和2.69 μm两种分辨率的图像数据,也即一个低分辨率的体素对应103个高分辨率体素,为柱塞样品低分辨率图像的处理提供了重要参照。

|
| 图 3 子样品与柱塞岩心图像三维配准结果 Figure 3 3D registration between sub-sample and core plug |
|
|
扫描完成的CT图像首先要经过滤波消除噪声影响,根据不同的成像效果选择不同的滤波算法,如中值滤波、非局部平均滤波[23]等。为了构建扫描样品的数字岩心模型,需要对扫描图像进行分割。对于多组分的数字岩心构建,图像分割分为两部分:孔隙分割与骨架分割。
3.1 孔隙分割孔隙分割分为两部分:高分辨率图像孔隙分割与低分辨率图像孔隙分割。常规数字岩心建模基于高分辨率图像分割进行,并假定岩心孔隙与岩石骨架完全可区分,利用二值分割将岩石分割为孔隙和骨架两相,并赋予0、1数字表示[24]。而实际情况下,当CT分辨率不足够高时,尺寸在分辨率以下的孔隙无法准确区分;如果仍然按照二值法分割,会造成孔隙度过小或者过大,与岩心真实孔隙结构有差异。对于低分辨率扫描图像,按照孔隙度的不同可以分割为孔隙、微孔隙和骨架三相。每一相以孔隙度来量化:孔隙的孔隙度为1,骨架的孔隙度为0,微孔隙的孔隙度介于0和1之间。
根据砂岩子样品的高分辨率扫描图像(图 1b),按照常规的分割方法进行二值分割划分出孔隙,结果如图 4所示。得到的子样品三维数字岩心孔隙度为12.2%,高于柱塞岩心的实验孔隙度10.5%。

|
| 图 4 子样品高分辨率图像孔隙分割结果 Figure 4 Segmentation of pores in high resolution image of sub-sample |
|
|
由于岩心子样品同时具有高低两种分辨率的图像数据,高分辨率图像分辨率是低分辨率图像分辨率的10倍,因此通过计算每一个低分辨率的体素对应的103个高分辨率体素的孔隙度,可以得到低分辨率扫描图像中灰度值与孔隙度的对应关系,结果如图 5所示。可以看出低分辨率体素的孔隙度随灰度变化成阶梯式分布,基于此分布可以得出三段式孔隙度公式:
 (6)
(6)

|
| 图 5 低分辨率图像灰度与孔隙度对应关系 Figure 5 Relationship between porosity and gray value in low resolution images |
|
|
式中:φ为孔隙度;T1为孔隙与微孔隙的分界阈值;T2为微孔隙与骨架的分界阈值;n为灰度值。通过对介于0和1之间的微孔隙散点进行拟合确定最佳关系式,并根据与上下边界交叉点确定分界阈值T1和T2。
将孔隙度公式应用于砂岩柱塞样品,得到柱塞样品的三维数字岩心孔隙模型。其中,可识别孔隙相孔隙度为7.74%,微孔隙相孔隙度为2.86%,总孔隙度为10.60%,与实验值相吻合。图 6a是在柱塞样品中选取的100×100的二维切片。图 6b是常规二值分割的结果,反映岩心中的可识别孔隙。图 6c是按照新的分割方法得到的结果,为了使结果显示更直观,将微孔隙相按孔隙度大小分为6档。孔隙度大于75%的微孔隙相较多地分布在大孔隙的边缘,部分是由于孔隙与骨架的边际模糊效应造成的。从图 6b看出低分辨率下可识别大孔隙是相互孤立的,而且经过分析其在三维空间中也是不连通的。而将微孔隙加入之后,连通性得到了明显的改善(图 6c),这也说明了微孔隙部分起着重要的渗流通道的作用。

|
| a.27 μm分辨率CT二维切片;b.常规二值分割结果;c.多值分割结果。 图 6 柱塞样品低分辨率图像孔隙分割结果 Figure 6 Segmentation of pores in low resolution image of core plug |
|
|
计算机断层扫描X射线衰减取决于样品中组分的密度,也即CT成像灰度值反映岩心密度的变化。在有岩心Qemscan矿物成像数据的情况下(图 7),利用常规多阈值分割方法可以对高分辨率CT图像的骨架矿物进行划分,并通过对比确定每个组分对应的实际矿物类型。利用与孔隙分割同样的方法,计算每一个低分辨率体素对应103个高分辨率体素的每种矿物的体积分数,进而得到低分辨率下每一种矿物的灰度展布概率分布,结果如图 8所示,图中列出了样品中含量最多的5种矿物。从矿物灰度展布可以看出,矿物成分与灰度值并非完全区分,相互之间存在交叉,但每一种矿物都存在一定的优势范围。在低分辨率下的骨架分割过程中,首先确定每一点的孔隙度值,然后再根据灰度值与矿物分布曲线给定各矿物体积分数。

|
| 图 7 岩心Qemscan矿物分析结果 Figure 7 Qemscan image of core sample |
|
|

|
| 图 8 柱塞岩心灰度分布与矿物组分关系图 Figure 8 Relationship between gray value and mineral components division |
|
|
岩心扫描图像经过孔隙分割和骨架分割处理之后,形成了具有不同尺度网格、不同组分构成的多尺度、多组分的数字岩心模型。相比于用0、1分别代表孔隙、骨架的常规模型,新模型对岩心的描述更全面、精确。对于新模型的任一格点Ω,可以给出其所包含的组分及各组分所占的比例,并满足公式:
 (7)
(7) 式中:N表示格点内组分的数目;fi表示第i种组分所占的比例。本文所用砂岩样品的分割包括孔隙和5种矿物,因此N=6。
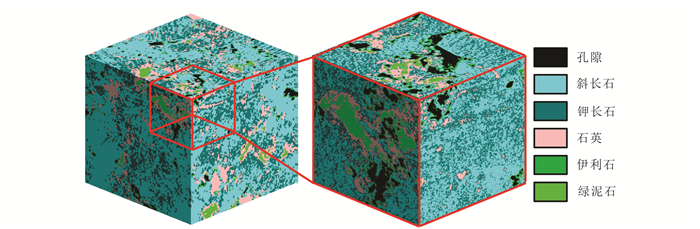
经过孔隙分割与骨架矿物分割,将岩心图像刻度为岩心组分的集合,便得到了多尺度、多组分的数字岩心模型,图 9为模型示意图。图 9左侧为粗尺度模型,为了便于可视化,将每一体素点表示为其中占比最大的组分。图 9右侧是细尺度模型,对应于粗尺度模型的一部分,每一体素点代表单一组分。图 9中孔隙均为相应分辨率下的可识别孔隙。
|
| 图 9 砂岩样品多尺度多组分数字岩心示意图 Figure 9 Example of multi-scale and -component digital core |
|
|
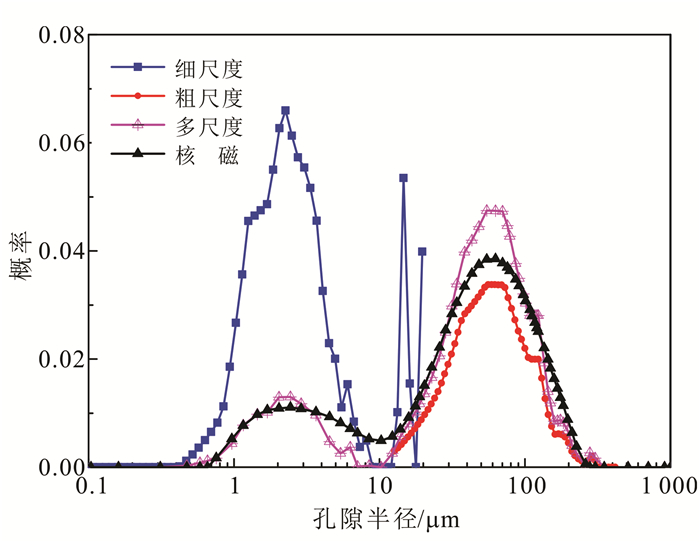
利用图像配准方法构建的多尺度数字岩心包含了多种分辨率的岩心结构信息,通过对原始模型重采样可以得到任意所需分辨率下的数字岩心模型,不同分辨率可以反映不同尺度的结构信息。通过对不同分辨率的数字岩心提取孔隙网络模型,可以统计不同尺度下的岩心孔隙分布特征。同样针对本文中的砂岩样品,对于高分辨率数字岩心,按照对应的低分辨率数据,将可识别大孔隙对应部分进行掩模处理,划分为骨架,这样高分辨率数字岩心得到的只是微孔隙对应的细尺度孔隙半径分布。对于低分辨数字岩心,将体素孔隙度大于0.9的部分视为孔隙,其余部分设为骨架。提取各自的孔隙网络模型可以得到粗细两种尺度下的孔隙半径体积概率分布。根据低分辨率数字岩心中大孔隙与微孔隙的体积比,本文中体积比为2.7,将粗尺度分布乘上体积比,与细尺度分布进行拼接,便可得到完整的多尺度孔隙半径分布。合成的多尺度孔隙半径分布与核磁T2谱分布有相似的双峰分布,因此通过二者的峰值点确定T2谱转换系数C,转换之后的核磁孔隙半径分布如图 10所示。由于数值模拟结果布点数较少,因此重新插值采用了与核磁结果相一致的布点方式。图 10中,4组曲线都经过了归一化处理,结果显示,多尺度数字岩心孔隙半径分布与核磁孔隙半径分布有较好的一致性。
|
| 图 10 样品孔隙半径概率分布曲线 Figure 10 Pore radius distribution curve of sandstone sample |
|
|
图 5与图 8反映了岩心柱塞样品低分辨率图像灰度与孔隙度和矿物组分的对应关系。两者孔隙相的分界阈值基本一致,大孔隙相反映的孔隙类型以粒间孔隙为主。微孔隙相对应的矿物组分为伊利石和斜长石,反映的是颗粒内溶孔、黏土矿物内溶孔及铸模孔等。
Qemscan矿物分析结果显示,砂岩样品中矿物体积分数在1%以上的共5种,矿物以长石为主,斜长石体积分数大于钾长石。表 1列出了5种矿物所占的比例。由于Qemscan只反映岩心二维截面的矿物分布,与X衍射测定结果略有差异,表现为石英、伊利石体积分数略低,钾长石体积分数略高。而多组分数字岩心得到矿物体积分数与X射线衍射分析结果吻合,也验证了多组分数字岩心构建的准确性。
| % | |||||
| 测定方式 | 石英 | 斜长石 | 钾长石 | 绿泥石 | 伊利石 |
| Qemscan | 33.40 | 47.37 | 15.28 | 1.94 | 2.01 |
| X衍射 | 37.46 | 49.43 | 8.70 | 1.13 | 3.28 |
| 多尺度数字岩心 | 38.31 | 50.55 | 6.85 | 1.15 | 3.14 |
利用基于特征的图像配准算法对岩心不同分辨率的扫描图像进行了精确匹配,采用多阈值分割方法对岩心孔隙、骨架矿物进行划分,构建了多尺度、多组分的数字岩心模型。
多尺度、多组分数字岩心模型克服了单一尺度数字岩心模型分辨率与岩心尺寸无法兼顾的困难,既能够表征岩心微观孔隙结构,也能够描述岩心宏观非均质性。通过多组分建模对岩心的孔隙结构、矿物分布进行全面的描述,在数值模拟中,可以仅提取孔隙结构进行渗流模拟,也可以选择性地提取某一种或几种组分进行电性、弹性模拟。通过多尺度数字岩心模型进行岩石物理属性的升尺度模拟,是将来研究的一个重要方向。
| [1] |
刘学锋, 张伟伟, 孙建孟. 三维数字岩心建模方法综述[J].
地球物理学进展, 2013, 28(6): 3066-3072.
Liu Xuefeng, Zhang Weiwei, Sun Jianmeng. Methods of Constructing 3-D Digital Cores:A Review[J]. Progress in Geophysics, 2013, 28(6): 3066-3072. DOI:10.6038/pg20130630 |
| [2] |
姚军, 赵秀才, 衣艳静, 等. 数字岩心技术现状及展望[J].
油气地质与采收率, 2005, 12(6): 52-54.
Yao Jun, Zhao Xiucai, Yi Yanjing, et al. The Current Situation and Prospect on Digital Core Technology[J]. Petroleum Geology and Recovery Efficiency, 2005, 12(6): 52-54. |
| [3] | Quiblier J A. A New Three-Dimensional Modeling Te-chnique for Studying Porous Media[J]. Journal of Colloid and Interface Science, 1984, 98(1): 84-102. DOI:10.1016/0021-9797(84)90481-8 |
| [4] | Roberts A. Statistical Reconstruction of Three-Dimen-sional Porous Media from Two-Dimensional Images[J]. Physical Review E, 1999, 56(3): 3203-3212. |
| [5] |
刘学锋, 孙建孟, 王海涛, 等. 顺序指示模拟重建三维数字岩心的准确性评价[J].
石油学报, 2009, 30(3): 391-395.
Liu Xuefeng, Sun Jianmeng, Wang Haitao, et al. The Accuracy Evaluation on 3D Digital Cores Reconstructed by Sequence Indicator Simulation[J]. Acta Petrolei Sinica, 2009, 30(3): 391-395. DOI:10.7623/syxb200903012 |
| [6] |
张丽, 孙建孟, 孙志强, 等. 多点地质统计学在三维岩心孔隙分布建模中的应用[J].
中国石油大学学报(自然科学版), 2012, 36(2): 105-109.
Zhang Li, Sun Jianmeng, Sun Zhiqiang, et al. Application of Multiple-Point Geostatistics in 3D Pore Structure Model Reconstruction[J]. Journal of China University of Petroleum, 2012, 36(2): 105-109. |
| [7] | Wu K, Nunan N, Crawford J W, et al. An Efficient Markov Chain Model for The Simulation of Heterogeneous Soil Structure[J]. Soil Science Society of America Journal, 2004, 68(2): 346-351. DOI:10.2136/sssaj2004.3460 |
| [8] | Kanit T, Forest S, Galliet I, et al. Determination of the Size of the Representative Volume Element for Random Composites:Statistical and Numerical Approach[J]. International Journal of Solids and Structures, 2003, 40(13): 3647-3679. |
| [9] | Gitman I M, Askes H, Sluys L J. Representative Vo-lume:Existence and Size Determination[J]. Engineering Fracture Mechanics, 2007, 74(16): 2518-2534. DOI:10.1016/j.engfracmech.2006.12.021 |
| [10] | Sok R M, Varslot T, Ghous A, et al. Pore Scale Characterization of Carbonates at Multiple Scales:Integration of MicroCT, BSEM and FIBSEM[J]. Petrophysics, 2010, 51(6): 379-387. |
| [11] | Khalili A D, Arns J Y, Hussain F, et al. Permeability Upscaling for Carbonates from the Pore Scale by Use of Multiscale X-Ray-CT Images[J]. SPE Reservoir Evaluation and Engineering, 2013, 16(4): 353-368. DOI:10.2118/152640-PA |
| [12] | Khalili A D, Yanici S, Cinar Y, et al. Formation Factor for Heterogeneous Carbonate Rocks Using Multi-Scale Xray-CT Images[J]. Journal of Engineering Research, 2013, 1(2): 5-28. |
| [13] |
王晨晨, 姚军, 杨永飞, 等. 碳酸盐岩双孔隙数字岩心结构特征分析[J].
中国石油大学学报(自然科学版), 2013, 37(2): 71-74.
Wang Chenchen, Yao Jun, Yang Yongfei, et al. Structure Characteristics Analysis of Carbonate Dual Pore Digital Rock[J]. Journal of China University of Petroleum, 2013, 37(2): 71-74. |
| [14] |
白斌, 朱如凯, 吴松涛, 等. 利用多尺度CT成像表征致密砂岩微观孔喉结构[J].
石油勘探与开发, 2013, 40(3): 329-333.
Bai Bin, Zhu Rukai, Wu Songtao, et al. Multi-Scale Method of Nano(Micro)-CT Study on Microscopic Pore Structure of Tight Sandstone of Yanchang Formation, Ordos Basin[J]. Petroleum Exploration and Development, 2013, 40(3): 329-333. DOI:10.11698/PED.2013.03.09 |
| [15] | Sain R. Numerical Simulation of Pore-Scale Hetero-geneity and Its Effects on Elastic, Electrical and Transport Properties[D]. Stanford:Stanford University, 2010. http://www.sciencedirect.com/science/article/pii/009830049190072L |
| [16] | Shabro V, Kelly S, Torres-Verdín C, et al. Pore-Scale Modeling of Electrical Resistivity and Permeability in FIB-SEM Images of Organic Mudrock[J]. Geophysics, 2014, 79(5): D289-D299. DOI:10.1190/geo2014-0141.1 |
| [17] |
邹才能, 朱如凯, 吴松涛, 等. 常规与非常规油气聚集类型、特征、机理及展望:以中国致密油和致密气为例[J].
石油学报, 2012, 33(2): 173-187.
Zou Caineng, Zhu Rukai, Wu Songtao, et al. Types, Characteristics, Genesis and Prospects of Conventional and Unconventional Hydrocarbon Accumulations:Taking Tight Oil and Tight Gas in China as an Instance[J]. Acta Petrolei Sinica, 2012, 33(2): 173-187. DOI:10.7623/syxb201202001 |
| [18] |
李易霖, 张云峰, 丛琳, 等. X-CT扫描成像技术在致密砂岩微观孔隙结构表征中的应用:以大安油田扶余油层为例[J].
吉林大学学报(地球科学版), 2016, 46(2): 379-387.
Li Yilin, Zhang Yunfeng, Cong Lin, et al. Application of X-CT Scanning Technique in the Characterization of Micro Pore Structure of Tight Sandstone Reservoir:Taking the Fuyu Oil Layer in Daan Oilfield as an Example[J]. Journal of Jilin University (Earth Sciense Edition), 2016, 46(2): 379-387. |
| [19] | HolzerL, Münch B, Rizzi M, et al. 3D-Microstru-cture Analysis of Hydrated Bentonite with Cryo-Stabilized Pore Water[J]. Applied Clay Science, 2010, 47(3): 330-342. |
| [20] | Latham S, Varslot T, Sheppard A. Image Regist-ration:Enhancing and Calibrating X-Ray Micro-CT Imaging[C]//International Symposium of the Society of Core Analysts. Abu Dhabi:[s. n.], 2008. |
| [21] | Lowe D G. Distinctive Image Feature from Scale-Invariant Key Points[J]. International Journal of Computer Vision, 2004, 60(2): 91-110. DOI:10.1023/B:VISI.0000029664.99615.94 |
| [22] | Buades A, Coll B, Morel J M. A Non-Local Al-gorithm for Image Denoising[C]//Computer Vision and Pattern Recognition, 2005.[S. l.]:IEEE, 2005:60-65. |
| [23] | Andrä H, Combaret N, Dvorkin J, et al. Digital Rock Physics Benchmarks:Part Ⅰ:Imaging and Segmentation[J]. Computers and Geosciences, 2013, 50(1): 25-32. |
| [24] | Koenderink J. The Structure of Images[J]. Biological Cybernetics, 1984, 50(5): 363-370. DOI:10.1007/BF00336961 |



