0 引言
地震波数值模拟是了解复杂地质条件下地震波传播规律的有效工具,可以用来指导地震观测系统设计、数据解释和检验地震数据处理方法。然而,受计算内存和计算时间的限制,在对波动方程进行数值求解时,我们总是在一个有限的空间区域进行计算,这样自然就引入了人为边界,从而产生人为边界反射。这些人为边界反射严重干扰了由反射界面和自由界面反射的有效波。为此,已经发展了多种消除人为边界反射的方法。Clayton等[1]在傍轴近似理论基础上导出了二维声波方程吸收边界条件,该吸收边界条件对特定的入射角和频率范围内的边界反射具有较好的吸收效果。Cerjan等[2]通过在计算边界附近引入损耗介质来衰减向外传播的波;由于在两个具有不同吸收系数损耗介质的界面上同样会产生反射,因此需要有较多的吸收层才能达到很好吸收效果。Berenger[3]针对电磁场有限域波动问题给出了一种高效的完全匹配层(PML)吸收边界条件,并证明该方法可以完全吸收来自各个方向、各种频率的电磁波,而不产生任何反射。目前人们已将PML思想引入到地震波数值模拟中,并发展了多种规则网格下的PML吸收边界条件[4-6]。
然而在实际地震勘探中,起伏地表和复杂构造是普遍存在的。为此,地球物理学家们提出了多种模拟起伏地表下地震波场的数值方法。其中有限差分法因其计算效率高、对内存需求较小而得到广泛应用。Jih等[7]为了研究高山和峡谷地区的地震波传播特点,对Ilan[8]提出的一种处理二维折线状起伏地表的有限差分法进行了改进;但是,该方法需要做复杂的坐标变换,且很难推广到三维情况下。Oprsal等[9]将真空法自由边界条件引入到阶梯状近似的起伏地表上;该方法的缺点是精度低,并且容易出现不稳定现象。Frankel等[10]提出了一种密度渐变方法,该方法实际上是对真空法的一种改进,同样使用阶梯网格对起伏地表进行近似;但是这种方法精度较低,而且会在阶梯状网格角点处引起虚假散射波。为了彻底消除阶梯状网格引起的虚假散射波,人们发展了曲线网格法[11-14]。Appelo等[15]提出了一种非常有效的曲线坐标系离散自由边界条件,并证明了该方法的有效性和稳定性。后来,Lan等[16]把该方法扩展到了三维各向异性介质的地震波数值模拟中。相比于矩形网格有限差分法,曲线网格法不仅可以有效消除阶梯状网格引起的虚假散射波,而且可以减少离散化时的网格点数,从而节省内存、提高计算效率。然而,到目前为止,有关曲线坐标系下PML吸收边界条件的文章还比较少。Festa等[17]首次将曲线坐标系下的PML吸收边界条件应用到谱元法地震波数值模拟中。Gao等[18]利用三角网格计算地震波场时提出了一种非规则网格PML吸收边界条件。
为了有效消除起伏地表下地震波数值模拟引起的边界反射,本文提出了一种适用于曲线坐标系下二阶弹性波方程的PML吸收边界条件,并将该边界条件应用到正交曲线坐标系下的地震波数值模拟中。文中采用孙建国等[19]提出的正交贴体网格对起伏地表模型进行网格剖分。由于边界条件在正交曲线坐标系下无需进行坐标旋转和插值运算,从而简化了计算过程,提高了计算精度。
1 方法原理笛卡尔坐标系下二维非均匀各向同性弹性波方程为
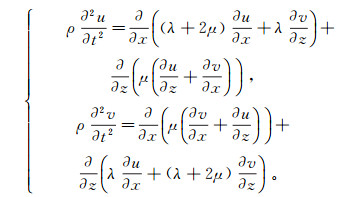 (1)
(1) 式中:u和v分别表示x、z方向上的位移;ρ为密度;λ和μ为lame系数。
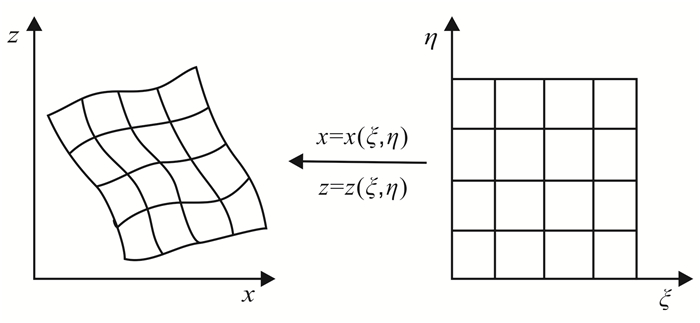
对于起伏地表下的地震波数值模拟,为了压制阶梯状网格引起的人为虚假散射波,网格线与起伏地表需要保持一致。这种网格被称为“贴体网格[20]”,已经有许多研究者在地震波数值模拟中采用了这种网格[15, 21-22]。贴体网格可以通过由计算空间到物理空间的坐标变换来获得(图 1)。通过这种变换,将曲线坐标系(ξ, η)映射成物理域上的笛卡尔直角坐标系。本文采用孙建国等[18]提出的方法生成正交贴体网格,具体的网格生成过程不做赘述。
|
| 图 1 网格映射示意图 Figure 1 Sketch of grid mapping |
|
|
通过生成贴体网格,笛卡尔坐标系下的每个网格点都由曲线坐标系唯一确定。因此,我们可以通过链式法则,由笛卡尔坐标系(x, z)下的波动方程得到曲线坐标系(ξ, η)下的波动方程。
根据链式法则,有
 (2)
(2) 式中:ξx、ξz、ηx、ηz分别表示∂ξ(x, z)/∂x、∂ξ(x, z)/∂z、∂η(x, z)/∂x、∂η(x, z)/∂z;∂x、∂ξ、∂z、∂η分别表示变量对x、ξ、z、η的偏导数。利用式(1)和式(2)可以得到曲线坐标系下的弹性波方程:
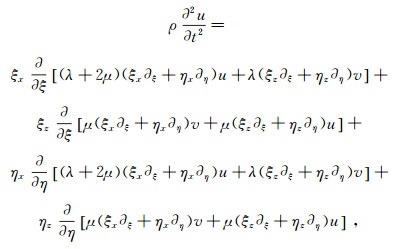 (3)
(3) 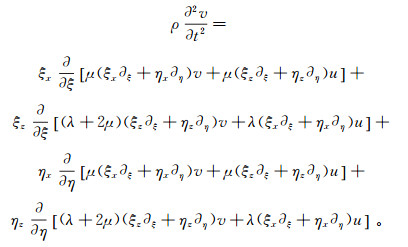 (4)
(4) 为了得到地震波在PML里的波动方程,把波动方程(3)、(4)变换到频率域,并对频率域里的波动方程做如下坐标拉伸变换[23]:
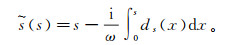 (5)
(5) 式中:

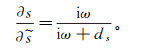 (6)
(6) 式中,ds≥0,是使地震波振幅在PML里指数衰减的系数。把式(6)带入到由式(3)和式(4)得到的复杂拉伸坐标系下的波动方程,得:
 (7)
(7) 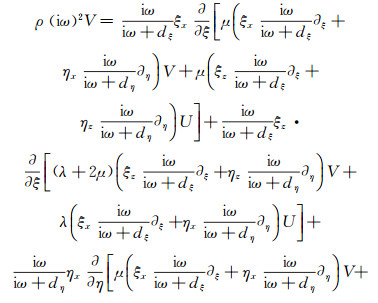
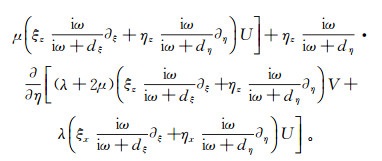 (8)
(8) 式中:U和V分别表示u和v对t的傅里叶变换;dξ=-(n+1)lg(R)(vP/(2δ))(ξ/δ)2[23],是ξ方向上的衰减系数;dη=-(n+1)lg(R)(vP/(2δ))·(η/δ)2是η方向上的衰减系数;vP为纵波速度,δ为PML的厚度,n为常数,用来控制衰减系数的变化率,通常取2~3,R是理论反射系数,通常取10-2~10-6。
利用波场分解技术[24],把位移水平分量分解成3个部分:U=U1+U2+U3,带入到方程(7)的左边,并把带入后的方程分解成如下3个方程:
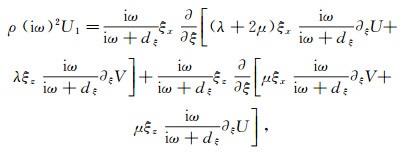 (9)
(9) 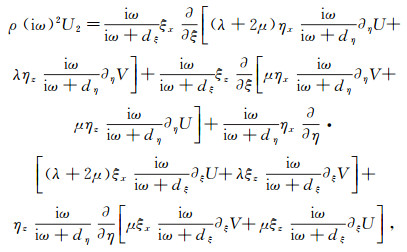 (10)
(10) 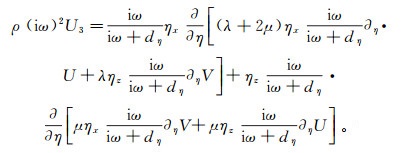 (11)
(11) 对方程(9)、(10)、(11)直接做反傅里叶变换,可以得到时间域PML方程,但是这样会引入卷积运算。为此我们用(iω+dξ)2、(iω+dξ)(iω+dη)和(iω+dη)2分别乘上方程(9)、(10)和(11)的两边,并引入两个中间变量R1和R2(见附录),再作反傅里叶变换,可以得到时间域PML吸收边界条件:
 (12)
(12) 式中:r1和r2分别表示R1和R2的反傅里叶变换;u=u1+u2+u3,u1、u2和u3分别表示U1、U2和U3的反傅里叶变换;∂t表示变量对时间t求导;dξ′=∂dξ/∂ξ;dη′=∂dη/∂η。
同理,把位移水平分量分解成3个部分:V=V1+V2+V3, 并引入两个中间变量R3和R4(见附录),可根据式(8)得到如下时间域PML方程:
 (13)
(13) 式中:r3和r4分别表示R3和R4的反傅里叶变换;v=v1+v2+v3,v1、v2和v3分别表示V1、V2和V3的反傅里叶变换。
由方程(12)和(13)可以看出,通过在频率域中引入中间变量R1、R2、R3和R4,可以避免将频率域里的PML方程转化到时间域时引起的卷积运算。
在计算域中利用PML吸收边界的基本方法如图 2所示。在常规区域,令dξ=dη=0,方程(12)和(13)退化成标准的波动方程(3)、(4)。在区域1中,令dξ≠0,dη=0;在区域2中,令dξ=0,dη≠0;在区域3中,令dξ≠0, dη≠0。这样在计算区域的左、右和底边界都有PML吸收介质,波由区域内通过边界传播到完全匹配层时不会产生任何反射。

|
| 图 2 PML吸收边界 Figure 2 Boundary of PML |
|
|
在顶边界我们采用自由界面条件。由于采用了正交贴体网格,因此可以直接实施笛卡尔坐标系下的自由边界条件,无需做复杂的坐标转换[25]。
2 有限差分格式由于波在PML区域内传播是逐步衰减的,故可以采用低精度的差分进行离散,因此方程(12)的差分格式可以写成:
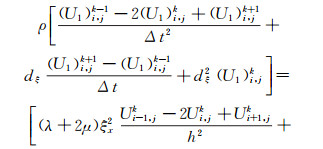
 (14)
(14)  (15)
(15) 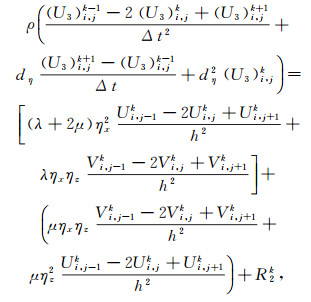 (16)
(16)  (17)
(17) 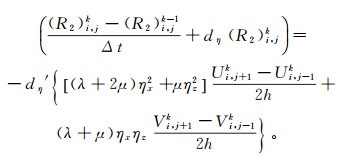 (18)
(18) 式中:(U1)i, jk、(U2)i, jk、(U3)i, jk、Ui, jk、Vi, jk、(R1)i, jk、(R2)i, jk分别表示u1、u2、u3、u、v、r1、r2在k时刻的离散值;h为空间网格步长;Δt为时间采样间隔。计算上述方程时,先根据Uk和Vk计算R1k和R2k,再计算U1k+1、U2k+1、U3k+1,最后根据Uk+1=U1k+1+U2k+1+U3k+1计算Uk+1。同理可以求取方程(13),具体过程不再赘述。
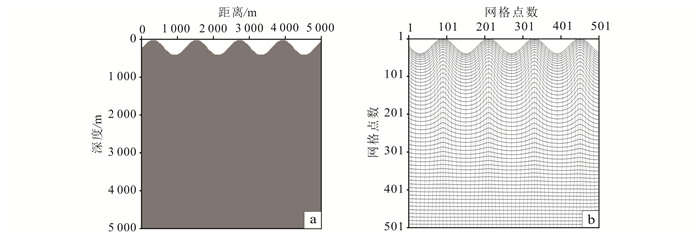
3 模型试算为了验证本文方法的有效性,我们设计了一个正弦函数起伏地表模型(图 3a)。该模型的地表可用正弦函数表示为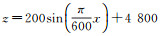
|
| a.正弦函数起伏地表模型;b.正交贴体网格剖分。 图 3 速度模型和网格剖分示意图 Figure 3 Velocity model and grid subdivision schemes |
|
|

|
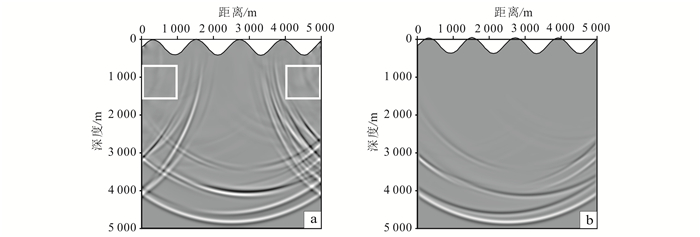
| a.无吸收边界;b.PML吸收边界。 图 4 t=1.6 s的水平分量波场快照 Figure 4 Horizontal component of snapshot at t=1.6 s |
|
|
|
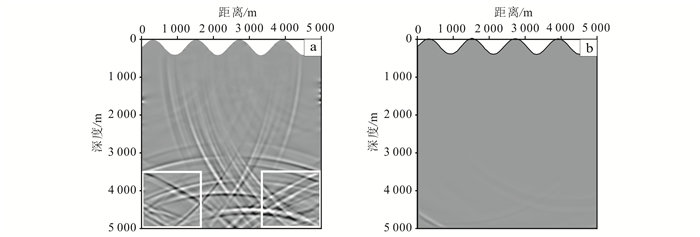
| a.无吸收边界;b.PML吸收边界。 图 5 t=1.6 s 的垂直分量波场快照 Figure 5 Vertical component of snapshot at t=1.6 s |
|
|
|
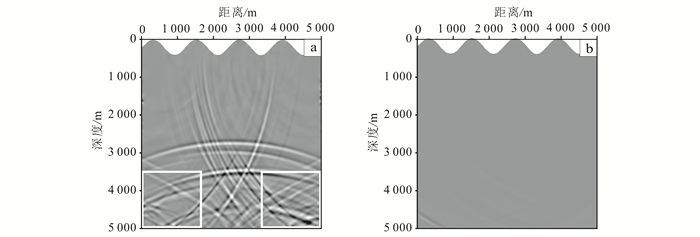
| a.无吸收边界;b.PML吸收边界。 图 6 t=2.4 s 的水平分量波场快照 Figure 6 Horizontal component of snapshot at t=2.4 s |
|
|
|
| a.无吸收边界;b.PML吸收边界。 图 7 t=2.4 s 的垂直分量波场快照 Figure 7 Vertical component of snapshot at t=2.4 s |
|
|
图 8和图 9是模拟地震记录的水平分量和垂直分量。由图 8、9可见:不加吸收边界时,波在边界上产生明显的边界反射;而采用PML吸收边界时,波在边界上几乎没有产生边界反射,而且对反射纵波和横波都有较好的吸收效果。

|
| a.无吸收边界;b.PML吸收边界。 图 8 水平分量地震记录 Figure 8 Record of horizontal component |
|
|

|
| a.无吸收边界;b.PML吸收边界。 图 9 垂直分量地震记录 Figure 9 Record of vertical component |
|
|
本文提出了一种曲线坐标系下的PML吸收边界条件,并结合有限差分法模拟了起伏地表条件下的地震波场。该方法通过在频率域中引入4个中间变量,避免了复杂的卷积运算。数值算例表明,本文提出的PML吸收边界对入射到人工边界的各种类型波都具有很好的吸收效果,保证了有效波场不受虚假反射波的干扰。
附录为了避免将频率域PML吸收方程变换到时间域时引起的卷积运算,引入4个中间变量:
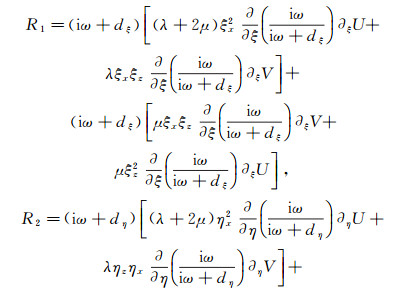
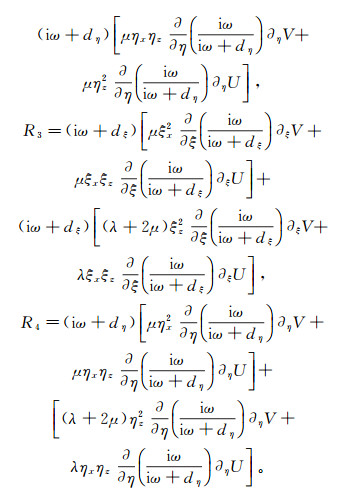
| [1] | Clayton R, Engquist B. Absorbing Boundary Conditi-ons for Acoustic and Elastic Wave Equations[J]. Bulletin of the Seismological Society of America, 1977, 67(6): 1529-1540. |
| [2] | Cerjan C, Kosloff D, Kosloff R, et al. A Nonreflecting Boundary Condition for Discrete Acoustic and Elastic Wave Equations[J]. Geophysics, 1985, 50(4): 705-708. DOI:10.1190/1.1441945 |
| [3] | Berenger J P. A Perfectly Matched Layer for the Ab-sorption of Electromagnetic Waves[J]. Journal of Computational Physics, 1994, 114(2): 185-200. DOI:10.1006/jcph.1994.1159 |
| [4] | Hastings F D, Schneider J B, Broschat S L. Appli-cation of the Perfectly Matched Layer (PML) Absorbing Boundary Condition to Elastic Wave Propagation[J]. The Journal of the Acoustical Society of America, 1996, 100(5): 3061-3069. DOI:10.1121/1.417118 |
| [5] | Collino F, Tsogka C. Application of the Perfectly Ma-tched Absorbing Layer Model to the Linear Elastodynamic Problem in Anisotropic Heterogeneous Media[J]. Geophysics, 2001, 66(1): 294-307. DOI:10.1190/1.1444908 |
| [6] | Zeng Y Q, He J Q, Liu Q H. The Application of the Perfectly Matched Layer in Numerical Modeling of Wave Propagation in Poroelastic Media[J]. Geophysics, 2001, 66(4): 1258-1266. DOI:10.1190/1.1487073 |
| [7] | Jih R S, McLaughlin K L, Der Z A. Free-Boundary Conditions of Arbitrary Polygonal Topography in a Two-Dimensional Explicit Elastic Finite-Difference Scheme[J]. Geophysics, 1988, 53(8): 1045-1055. DOI:10.1190/1.1442541 |
| [8] | Ilan A. Finite-Difference Modeling for P-Pulse Propa-gation in Elastic Media With Arbitrary Polygonal Surface[J]. Journal of Geophysics, 1977, 43(1/2): 41-58. |
| [9] | Opršal I, Zahradnik J. Elastic Finite-Difference Me-thod for Irregular Grids[J]. Geophysics, 1999, 64(1): 240-250. DOI:10.1190/1.1444520 |
| [10] | Frankel A, Leith W. Evaluationof Topographic Eff-ects on P and S-Waves of Explosions at the Northern Novaya Zemlya Test Site Using 3-D Numerical Simulations[J]. Geophysical Research Letters, 1992, 19(18): 1887-1890. DOI:10.1029/92GL02147 |
| [11] | Hestholm S, Ruud B. 2D Finite-Difference Elastic Wave Modelling Including Surface Topography[J]. Geophysical Prospecting, 1994, 42(5): 371-390. DOI:10.1111/gpr.1994.42.issue-5 |
| [12] | Hestholm S, Ruud B. 3-D Finite-Difference Elastic Wave Modeling Including Surface Topography[J]. Geophysics, 1998, 63(2): 613-622. DOI:10.1190/1.1444360 |
| [13] | Tessmer E, Kosloff D, Behle A. Elastic Wave Propa-gation Simulation in the Presence of Surface Topography[J]. Geophysical Journal International, 1992, 108(2): 621-632. DOI:10.1111/gji.1992.108.issue-2 |
| [14] |
李庆洋, 李振春, 黄建平, 等. 基于贴体全交错网格的起伏地表正演模拟影响因素[J].
吉林大学学报(地球科学版), 2016, 46(3): 920-929.
Li Qingyang, Li Zhenchun, Huang Jianping, et al. Factor Analysis of Seismic Modeling with Topography Based on a Fully Staggered Body-Fitted Grids[J]. Journal of Jilin University (Earth Science Edition), 2016, 46(3): 920-929. |
| [15] | Appelö D, Petersson N A. A Stable Finite Difference Method for the Elastic Wave Equation on Complex Geometries with Free Surfaces[J]. Communications in Computational Physics, 2009, 5(1): 84-107. |
| [16] | Lan H, Zhang Z. Three-Dimensional Wave-Field Si-mulation in Heterogeneous Transversely Isotropic Medium with Irregular Free Surface[J]. Bulletin of the Seismological Society of America, 2011, 101(3): 1354-1370. DOI:10.1785/0120100194 |
| [17] | Festa G, Vilotte J P. The Newmark Scheme as Ve-locity-Stress Time-Staggering:An Efficient PML Implementation for Spectral Element Simulations of Elastodynamics[J]. Geophysical Journal International, 2005, 161(3): 789-812. DOI:10.1111/gji.2005.161.issue-3 |
| [18] | Gao H, Zhang J. Implementationof Perfectly Matched Layers in an Arbitrary Geometrical Boundary for Elastic Wave Modelling[J]. Geophysical Journal International, 2008, 174(3): 1029-1036. DOI:10.1111/gji.2008.174.issue-3 |
| [19] |
孙建国, 蒋丽丽. 用于起伏地表条件下地球物理场数值模拟的正交曲网格生成技术[J].
石油地球物理勘探, 2009, 44(4): 494-500.
Sun Jianguo, Jiang Lili. Orthogonal Curvilinear Grid Generation Technique Used for Numeric Simulation of Geophysical Fields in Undulating Surface Condition[J]. Oil Geophysical Prospecting, 2009, 44(4): 494-500. |
| [20] | Hvid S L. Three Dimensional Algebraic Grid Gene-ration[M]. Kongens Lyngby: Technical University of Denmark, 1995. |
| [21] | Fornberg B. Generation of Finite Difference Formulas on Arbitrarily Spaced Grids[J]. Mathematics of Computation, 1988, 51(184): 699-706. DOI:10.1090/S0025-5718-1988-0935077-0 |
| [22] | Lan H Q, Zhang Z J. Seismic Wavefield Modeling in Media with Fluid-Filled Fractures and Surface Topography[J]. Applied Geophysics, 2012, 9(3): 301-312. DOI:10.1007/s11770-012-0341-5 |
| [23] | Collino F, Tsogka C. Application of the Perfectly Matched Absorbing Layer Model to the Linear Elastodynamic Problem in Anisotropic Heterogeneous Media[J]. Geophysics, 2001, 66(1): 294-307. DOI:10.1190/1.1444908 |
| [24] | Collino F, Monk P. The Perfectly Matched Layer in Curvilinear Coordinates[J]. SIAM Journal on Scientific Computing, 1998, 19(6): 2061-2090. DOI:10.1137/S1064827596301406 |
| [25] |
丘磊, 田钢, 石战结, 等. 起伏地表条件下有限差分地震波数值模拟:基于广义正交曲线坐标系[J].
浙江大学学报(工学版), 2012, 46(10): 1923-1931.
Qiu Lei, Tian Gang, Shi Zhanjie, et al. Finite-Difference Method for Seismic Wave Numerical Simulation in Presence of Topography[J]. Journal of Zhejiang University (Engineering Scinice), 2012, 46(10): 1923-1931. DOI:10.3785/j.issn.1008-973X.2012.10.027 |



