0 引言
探地雷达(ground penetrating radar, GPR)[1]是一种对探测目标无损伤的探测方法,经常用于埋藏物的探测和近地表地下结构的评估。GPR通过天线向地下发射高频电磁波、接收回波来分析近地表的地质构造。由于GPR接收天线接收的频带较宽,观测环境复杂,导致GPR接收到的信号中通常混有很强的噪声[2-4]。在实际勘探中,遇到的随机噪声包含雷达的自身干扰、自然界的电磁波、人为因素产生的机械振动等。
目前,大部分探地雷达数据随机噪声压制方法来源于地震勘探数据处理技术。常用的随机噪声压制方法包括f-x域去噪[5]、频率域滤波、Radon域去噪[6]等。20世纪80年代发展起来的小波变换[7]在图像分析去噪方面取得了良好的效果。小波变换作为一种多尺度变换,虽然能够更稀疏地表示一维分段函数或有界变换函数,但是它在一维时具有的优异特性却不能简单地推广到二维或高维信号。为了克服小波变换对高维信号边缘信息表达能力存在的局限性,更好地分析二维或高维信号,多尺度几何分析方法得到了迅速发展。其中,楔形波(Wedgelet)[8-9]、梳状波(Brushlet)[10]、子束波(Beamlet)[11]和条带波(Bandelet)[12]的自适应多尺度几何分析方法,以及脊波(Ridgelet)[13]、轮廓波(Contourlet)[14]和曲波(Curvelet)[15-17]等非自适应多尺度几何分析方法,在二维或高维信号稀疏表示和图像分析方面发挥了重要作用。
2006年,Guo K等[18-20]提出了一种新的多尺度几何分析方法——剪切波(Shearlet)变换。在复合小波理论和几何多尺度分析理论的基础上,特殊形式的合成膨胀仿射系统构造了Shearlet变换。在Shearlet变换系统中,有两个矩阵:一个是抛物矩阵,它控制着尺度;另一个是剪切矩阵,它控制着方向。因此,在用Shearlet表示高维信号时,它能够准确地描述高维信号的尺度、方向和位置信息。作为一种新型多尺度几何分析算法,Shearlet变换具有较好的局部化特性,在频率域上是紧支撑的,而且具有很强的方向敏感性。对信号进行Shearlet变换,变换系数与原始信号大小相同,图像位置具有一一对应的关系,说明Shearlet变换对尺度方向表征更加细腻,变换系数物理意义更加明确[21]。
Shearlet变换凭借自身的优越性,在各领域得到了快速的发展。Easley等[22]利用离散Shearlet变换的稀疏性进行图像的稀疏表示;Yi等[23]将Shearlet变换结合到图像检测方面;魏扬等[24]利用Shearlet变换的多尺度性进行医学图像的融合处理;朱华生等[25]和胡海智等[26]将Shearlet变换应用于图像去噪,取得了良好的效果;刘成明等[27]将Sheatlet变换引入到地震数据随机噪声压制的研究中,并将Shearlet变换结果与一些常规去噪方法得到的结果进行对比,体现了Sheatlet变换在去除随机噪声方面的优势。随后,他又进行了Shearlet域稀疏约束地震数据重构的研究,同样取得了良好的效果[28]。
本文鉴于Shearlet变换在图像几何分析方面的优势,将其用来解决GPR数据的随机噪声压制问题。根据Shearlet变换的多尺度、多方向性,将GPR数据转换到Shearlet域。在Shearlet域,有效信号的Shearlet系数较大,随机噪声的Shearlet系数较小,利用硬阈值方法去除较小的Shearlet系数,再进行Shearlet反变换,就得到了随机噪声压制以后的GPR数据。最后利用常规的f-x域去噪、中值滤波和小波变换去噪方法与Shearlet变换硬阈值去噪方法进行对比。
1 Shearlet变换 1.1 连续Shearlet变换Shearlet变换是一种多尺度、多角度的几何分析方法,它包含了一个尺度矩阵Aa,a为尺度参数,a > 0,根据抛物尺度准则划分尺度,还包含一个剪切矩阵Ss,s为剪切参数,s∈R,用来进行方向剖分,分别定义如下:
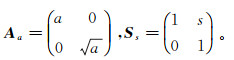 (1)
(1) 为了保证不同方向的剖分效果相同,将频率域按方向划分为4个区域C1-C4和1个中心区域R,分别定义如下:
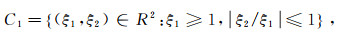 (2-1)
(2-1) 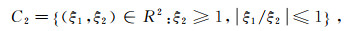 (2-2)
(2-2)  (2-3)
(2-3) 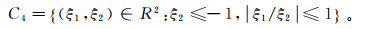 (2-4)
(2-4) 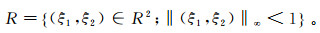 (3)
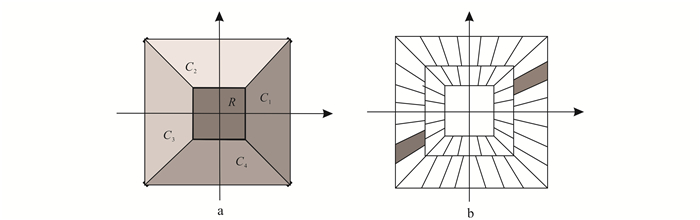
(3) 信号的低频部分主要集中于中心R。图 1a给出了频率域的剖分结构,C1和C3表示水平区域,C2和C4表示垂直区域。图 1b展示了如何剖分区域C1-C4,水平区域C1、C3和垂直区域C2、C4的剖分是相同的,灰色梯形展示了水平区域C1和C3剖分的一对Shearlet基。
|
| 图 1 频率域区域划分(a)及离散Shearlets剖分(b) Figure 1 Frequency domain division (a) and discrete Shearlets subdivision (b) |
|
|
连续Shearlet系统

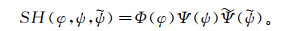 (4)
(4) 其中:
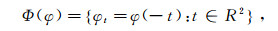 (5)
(5) 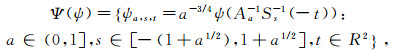 (6)
(6) 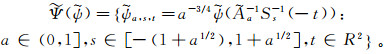 (7)
(7) 式中,t为平移参数。令
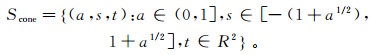 (8)
(8) 那么,当
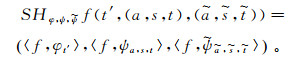 (9)
(9) 式中:f∈L2(R2);t′为平移参数;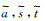
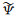
Shearlet变换的离散化,是通过对连续Shearlet变换参数的采样获得的。对于水平区域C1∪C3,Scone离散化为
 (10)
(10) 式中:c=(c1, c2)∈(R+)2;j,k,m表示采样参数;Mc为采样矩阵。Mc定义为
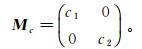 (11)
(11) 对于垂直区域C2∪C4,以类似的方式对Scone进行离散化,所使用的采样矩阵为
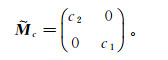 (12)
(12) 常规的Shearlet离散系统

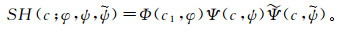 (13)
(13) 其中,
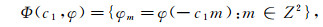 (14)
(14) 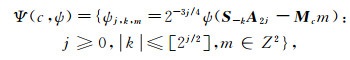 (15)
(15) 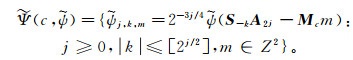 (16)
(16) 令
 (17)
(17) 那么,当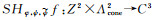
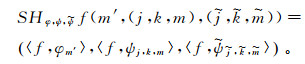 (18)
(18) 式中,函数f∈L2(R2)。
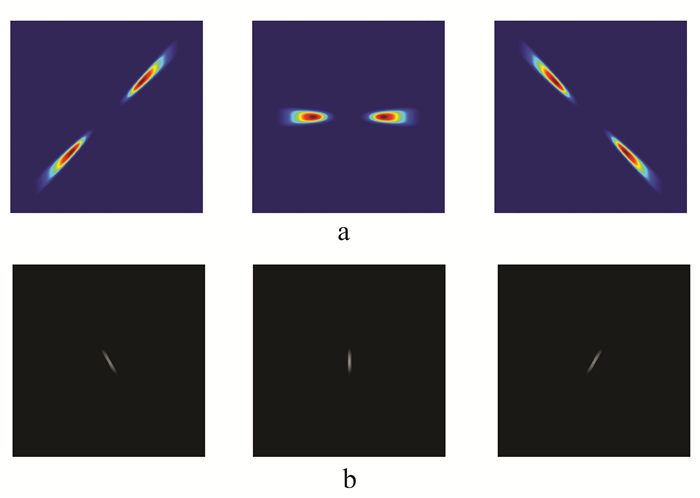
图 2展示了Shearlet基不同方向的形态。说明了Shearlet变换优越的多尺度、多方向特性,它可以用最优的形式来表示高维信号。同时,Shearlet变换比常规变换具有更好的稀疏性[29]。因此,我们将其应用于GPR数据处理中,结合快速阈值迭代算法,来压制GPR数据中的随机噪声。
|
| a.频率域;b.时间域。 图 2 第三尺度下的Shearlet基 Figure 2 Shearlet base in the third scale |
|
|
Shearlet变换的分解由两步构成:多尺度剖分和方向局部化。
1) 多尺度剖分。用Haar小波对图像进行分解,对于图像g,分别得到低频系数x′a和各尺度下的高频系数x0,x1,...,xa(a为分解尺度)。
2) 方向局部化。为了得到不同方向的高频分量,对各尺度下的高频系数采用带方向和尺度变化的窗函数进行剖分。对每个尺度上的高频系数区域,水平区域D0和垂直区域D1分别选择2j+1+1个窗函数W,满足
 (19)
(19) 式中:d为区域参数;l为角度数量。
Shearlet变换的重构过程包含子带重构和图像重构。
1) 子带重构。将分解得到的Shearlet系数x进行方向局部化反变换,对不同尺度下的子带分别进行重构并相加,即可得到重构后的高频系数Δxa。
2) 图像重构。对分解后的低频系数x′a与重构后的高频系数Δxa按位置进行合成,从而可以得到重构后的图像Δg。
由于Shearlet变换具有多方向性:当Shearlet方向与GPR信号方向大致相同时,可以得到较大的Shearlet系数;相反,当Shearlet基函数方向与GPR信号方向偏差较大时,得到的Shearlet系数较小。在实际GPR数据处理中,将GPR数据变换到Shearlet域时,有效信号的Shearlet系数较大,而随机信号不具方向性,Shearlet系数较小;所以,利用一个阈值函数去除较小的Shearlet系数,从而达到去除随机噪声的目的,再进行Shearlet反变换,得到压制随机噪声以后的GPR数据。
本文选取硬阈值函数T(x),其定义为
 (20)
(20) 式中:C为常数变量;λ为Shearlet系数的均方根,需根据尺度和角度的不同分别进行计算;σ为噪声的标准差。由于GPR信号被分解在Shearlet域的不同尺度和不同角度下,此种条件下所含的GPR信号是不同的,所以,根据硬阈值函数计算出来的阈值也是不同的,这样可以最大程度地压制随机噪声。
与硬阈值相比,软阈值函数是将所有的系数减去计算出来的阈值,在压制随机噪声的同时,损伤了部分有效信号,降低了数据的峰值信噪比,所以本文选择硬阈值函数。
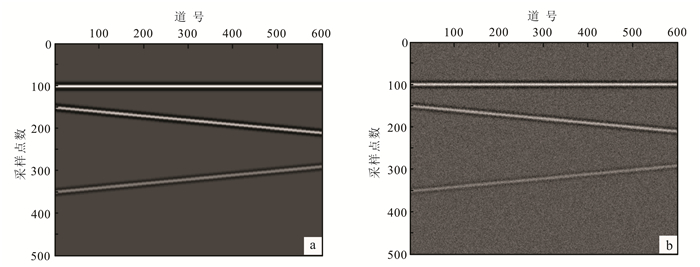
3 理论数据试算为了验证Shearlet变换阈值去噪方法的有效性,本文首先利用一个简单的GPR理论数据,将其与常用的中值滤波、f-x域去噪和小波变换去噪方法进行对比。如图 3a所示,理论模型包含4层,3个反射界面(1个水平界面和2个倾斜界面),并且3个反射界面具有不同的振幅。本文利用雷克子波与反射系数褶积来合成理论模型的GPR数据。然后,将理论数据加入一定的高斯白噪声,信噪比为10.076 4 dB,用来测试去噪方法的性能,如图 3b所示。
|
| a.理论GPR数据;b.理论GPR数据加噪。 图 3 理论GPR测试数据 Figure 3 Simulation of GPR data |
|
|
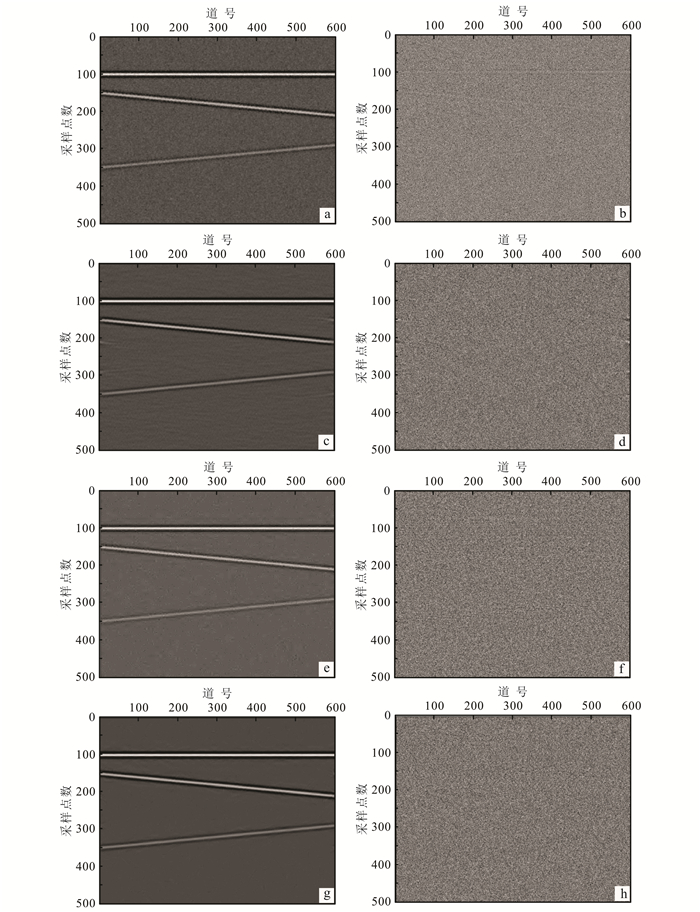
分别利用中值滤波、f-x域去噪、小波变换去噪和本文提出的Shearlet变换阈值去噪方法对加入随机噪声的理论GPR数据进行处理,结果如图 4所示。中值滤波方法(窗口尺寸为3×3)去除了大部分随机噪声,但合成的GPR数据图像不够清晰(图 4a),而且从它的差剖面中可以发现有效信号的痕迹(图 4b),说明中值滤波方法对有效信号有损伤。f-x域去噪方法随机噪声压制效果较好,但仍有残留,同时,还产生了一些不明显的假象(图 4c);其对应的差剖面几乎没有有效信号的痕迹(图 4d)。小波变换去噪方法选用的尺度为4阶,其结果要好于中值滤波结果,随机噪声得到了较为充分地压制,但仍然存在一定的残留(图 4e);其所对应的差剖面几乎没有有效信号的痕迹(图 4f)。Shearlet变换阈值去噪方法选用的尺度为4阶,随机噪声得到了充分压制,GPR理论数据图像变得非常清晰,与原始理论数据非常相近(图 4g);其差剖面中没有有效信号的存在(图 4h)。
|
| a.中值滤波;b.中值滤波差剖面;c. f-x域去噪;d. f-x域去噪差剖面;e.小波变换;f.小波变换差剖面;g. Shearlet变换;h. Shearlet变换差剖面。 图 4 去噪结果及其差剖面 Figure 4 result and residual profile |
|
|
利用均方根误差(mean squared error,MSE)、信噪比(signal-to-noise ratio,SNR)和峰值信噪比(peak signal-to-noise ratio,PSNR)对3种方法进行对比,结果如表 1所示。由表 1可知,Shearlet变换所得结果信噪比提高得最多,约4 dB,与原始数据的均方根误差最小,而且峰值信噪比最高;说明Shearlet变换阈值去噪方法所得结果具有高信噪比、高保真度。
| SNR/dB | PSNR | MSE | |
| 理论GPR数据 | 10.076 4 | 74.164 0 | 0.002 50 |
| 中值滤波 | 11.205 5 | 81.671 9 | 0.000 44 |
| f-x域去噪 | 11.211 3 | 86.145 0 | 0.000 15 |
| 小波变换 | 11.573 1 | 83.381 8 | 0.000 29 |
| Shearlet变换 | 14.634 0 | 91.801 9 | 0.000 04 |
由此可知,中值滤波、f-x域去噪和小波变换去噪方法都能去除部分随机噪声,但是并不彻底,f-x域去噪有时还会产生假象,中值滤波对有效信号有一定损伤。与Shearlet变换相比,虽然小波变换去噪方法具有多尺度的特性,但是其不具有方向特性。Shearlet变换具有多尺度、多方向的特性,在Shearlet域,GPR数据变得更加稀疏,有效信号和随机噪声得到了更好的分离,使得随机噪声的压制更加充分,更好地保留了有效信号,达到了随机噪声压制的目的。
为了验证Shearlet变换阈值去噪方法对随机噪声的压制能力,逐渐降低理论GPR数据的信噪比。当信噪比小于4.248 9 dB时,GPR数据有效信号受到严重损失,Shearlet变换阈值去噪方法无法对第三个界面进行有效识别。
4 实际数据测试在理论数据得到了验证的前提下,本文利用实际GPR数据对Shearlet变换阈值去噪方法进行验证。发射天线为100 MHz,采样频率为2 487.375 MHz,采样点数为1 494个,空间采样间隔为0.1 m,共360道。观察可知,原始实际GPR数据剖面(图 5a)中含有一定程度的随机噪声,影响了剖面成像的整体效果;剖面上层有效信号能量较强,受随机噪声干扰较小,剖面中层及下层能量较弱,受随机噪声干扰较为严重;层界面之间变得模糊,同相轴连续性较差。
|
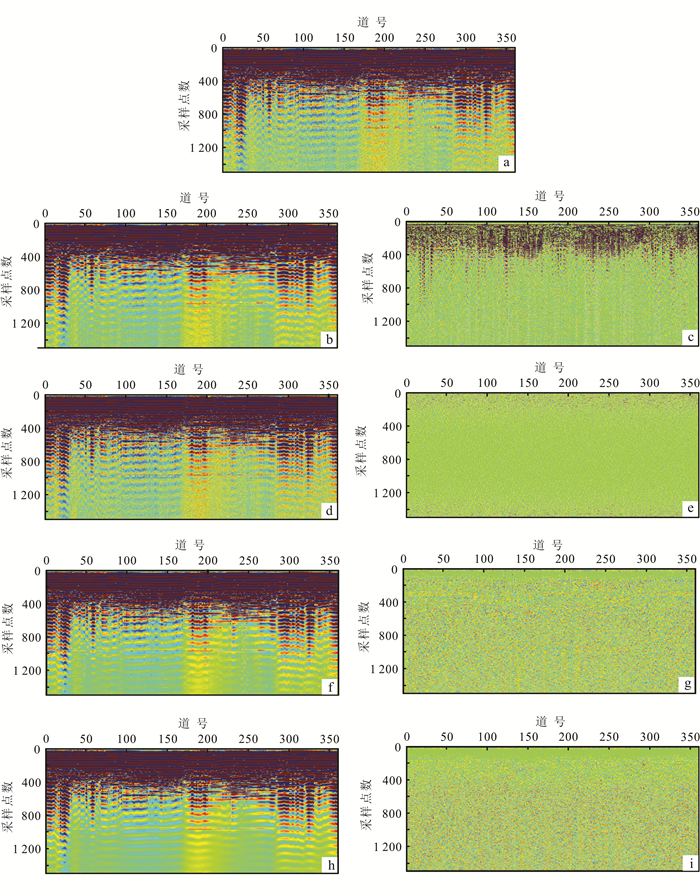
| a.原始实际GPR数据;b.中值滤波;c.中值滤波差剖面;d. f-x域去噪;e. f-x域去噪差剖面;f.小波变换;g.小波变换差剖面;h. Shearlet变换;i. Shearlet变换差剖面。 图 5 实际GPR数据去噪结果及其差剖面 Figure 5 Field GPR data and denoising result |
|
|
分别利用中值滤波、f-x域去噪、小波变换去噪和Shearlet变换阈值去噪方法处理实际GPR数据剖面。中值滤波去噪方法所用窗口尺寸仍然为3×3,与原始实际GPR数据相比,中值滤波去噪方法随机噪声压制效果并不明显(图 5b);从其差剖面(图 5c)可知,随机噪声得到可一定程度的压制,但同时损失了部分有效信号。f-x域去噪方法随机噪声压制效果较差,仅去除了小部分随机噪声(图 5d);从其差剖面可知,有效信号损失严重(图 5e)。小波变换去噪方法所用尺度仍为4阶,随机噪声的压制效果得到了明显的提升(图 5f);从其差剖面(图 5g)可知,有效信号的损失得到了减弱。Shearlet变换阈值去噪方法的所用尺度仍为4阶,随机噪声得到了较为彻底的压制,图像变得非常清晰,中深部反射同相轴变得更加容易识别,同相轴的连续性得到提升(图 5h);其差剖面(图 5i)几乎没有有效信号的损失。
5 结论1) 本文将Shearlet变换应用于GPR数据的去燥研究,根据Shearlet变换的稀疏特性压制随机噪声,通过理论与实际数据的试验,说明了Shearlet变换阈值去燥方法应用于GPR数据的有效性和适用性。
2) 通过与常规中值滤波、f-x域去噪和小波变换GPR数据随机噪声压制方法相比,Shearlet变换阈值去噪方法得到了更好的随机噪声压制效果,取得了令人更加满意的效果。同时,对有效信号的保留更好,充分体现了Shearlet变换阈值去噪方法高保真度的特性,以及优越性。
3) Shearlet变换阈值去燥方法的发展,对于从GPR数据中进行弱信号提取具有重大的促进作用,对研究近地表地质构造具有重大的研究意义与应用价值。
| [1] |
曾照发, 刘四新, 王者江, 等.
探地雷达方法原理及应用[M]. 北京: 科学出版社, 2006.
Zeng Zhaofa, Liu Sixin, Wang Zhejiang, et al. Ground Penetrating Radar:Principle and Application[M]. Beijing: Science Press, 2006. |
| [2] |
邹海林, 宁书年, 邹华胜. 采用不同预处理方法的GPR图像去噪效果分析[J].
地球物理学进展, 2005, 20(2): 469-475.
Zou Hailin, Ning Shunian, Zou Huasheng. Perfoemance Analysis of GPR Image De-Noising Based on Different Pre-Processing Methods[J]. Progress in Geophysics, 2005, 20(2): 469-475. |
| [3] | Baili J, Lahouar S, Hergli M, et al. GPR Singal De-Noising by Discrete Wavelet Transform[J]. NDT&E International, 2009, 42: 696-703. |
| [4] | Jeng Y, Li Y W, Chen C S, et al. Adaptive Filtering of Random Noise in Near-Surface Seismic and Ground Penetrating Radar Data[J]. Journal of Applied Geophysics, 2009, 68: 36-46. DOI:10.1016/j.jappgeo.2008.08.013 |
| [5] |
康冶, 于承业, 贾卧, 等. f-x域去噪方法研究[J].
石油地球物理勘探, 2003, 38(2): 136-138.
Kang Ye, Yu Chengye, Jia Wo, et al. f-x Domain De-Noising Research[J]. Oil Geophysical Prospecting, 2003, 38(2): 136-138. |
| [6] | Russel B, Hampson S, Chun J. Noise Elimination and the Radon Transform:Part 1[J]. The Leading Edge, 1990, 11(9): 31-37. |
| [7] |
张军华, 陆基孟. 小波变换方法在地震资料中去噪和提高分辨率中的应用[J].
石油大学学报(自然科学版), 1997, 21(1): 18-21.
Zhang Junhua, Lu Jimeng. Application of Wavelet Transform in Removing Noise and Improving Resolution of Seismic Data[J]. Journal of University of Petroleum (Edition of Natural Science), 1997, 21(1): 18-21. |
| [8] | Mckemma J, Boyd G D, Thurston R N. Plate Theory Solution for Guided Flexural Acoustic Waves Along the Tip of a Wedge[J]. IEEE Transactions on Sonics and Ultrasonics, 1974, 21(3): 178-186. DOI:10.1109/T-SU.1974.29812 |
| [9] | Mckemma J, Mckenna J. Flexural Acoustic Waves Along the Edge of a Plate[J]. IEEE Transactions on Sonics and Ultrasonics, 1974, 21(4): 296-297. DOI:10.1109/T-SU.1974.29830 |
| [10] |
段志强. 梳状波在频谱分析仪中的应用研究[J].
电子质量, 2010, 12: 47-56.
Duan Zhiqiang. Research on Application of the Comb Wave in the Spectrum Analyzer[J]. Assessmnet and Application, 2010, 12: 47-56. DOI:10.3969/j.issn.1003-0107.2010.05.018 |
| [11] |
杨明, 尹勇, 彭玉华, 等. Beamlet变换与多尺度线特征提取[J].
电子学报, 2007, 35(1): 100-103.
Yang Ming, Yin Yong, Peng Yuhua, et al. Beamlet Transform and Multiscale Linear Feature Extraction[J]. Acta Electronica Sinica, 2007, 35(1): 100-103. |
| [12] |
杨晓慧, 焦李成, 李伟. 基于第二代bandelets的图像去噪[J].
电子学报, 2006, 34(11): 2063-2067.
Yang Xiaohui, Jiao Licheng, Li Wei. Second Generation Bandelets Based Image Denoising[J]. Acta Electronica Sinica, 2006, 34(11): 2063-2067. DOI:10.3321/j.issn:0372-2112.2006.11.027 |
| [13] |
包乾宗, 高静怀, 陈文超. 面波压制的Ridgelet域方法[J].
地球物理学报, 2007, 50(4): 1210-1215.
Bao Qianzong, Gao Jinghuai, Chen Wenchao. Ridgelet Domain Method of Ground-Roll Suppression[J]. Chinese Journal of Geophysics, 2007, 50(4): 1210-1215. |
| [14] | Do M N, Vetterli M. The Contourlet Transform:An Efficient Directional Multiresolution Image Representation[J]. IEEE Trans Image Process, 2005, 14: 2091-2106. DOI:10.1109/TIP.2005.859376 |
| [15] |
仝中飞, 王德利, 刘冰. 基于Curvelet变换阈值法的地震数据去噪方法[J].
吉林大学学报(地球科学版), 2008, 38(增刊1): 48-52.
Tong Zhongfei, Wang Deli, Liu Bing. Seismic Data Denoise Based on Curvelet Transform with the Threshold Method[J]. Hournal of Jilin University (Earth Science Edition), 2008, 38(Sup.1): 48-52. |
| [16] |
王德利, 仝中飞, 唐晨, 等. Curvelet阈值迭代法地震随机噪声压制[J].
应用地球物理, 2010, 7(4): 315-324.
Wang Deli, Tong Zhongfei, Tang Chen, et al. An Iterative Curvelet Thresholding Algorithm for Seismic Random Noise Attenuation[J]. Applied Geophysics, 2010, 7(4): 315-324. |
| [17] |
孟阁阁, 王德利, 陈鑫. 基于三维曲波变换的地震数据去噪方法研究[J].
石油物探, 2014, 53(3): 314-323.
Meng Gege, Wang Deli, Chen Xin. Study on Seismic Data Denoising Method Based on 3D Curvelet Transform[J]. Geophysical Prospecting Forpetroleum, 2014, 53(3): 314-323. |
| [18] | Guo K, Labate D, Lim W, et al. Wavelets with Composite Dilations and Their MRA Properties[J]. Appl Comput Harmon Anal, 2006, 20: 202-236. DOI:10.1016/j.acha.2005.07.002 |
| [19] | Guo K, Labate D, Lim W, et al. The Theory of Wavelets with Composite Dilations[J]. Harmonic Analysis and Applications, 2006, 78: 231-250. |
| [20] | Guo K, Labate D, Lim W, et al. Wavelets with Composite Dilations[J]. Electron Res Announc Amer Math Soc, 2004, 10: 78-87. DOI:10.1090/S1079-6762-04-00132-5 |
| [21] |
王德营, 李振春, 黄建平, 等. 一种分尺度的面波压制方法[J].
石油学报, 2014, 35(2): 303-309.
Wang Deying, Li Zhenchun, Huang Jianping, et al. A Surface Wave Suppression Method Based on Scale-Partition[J]. Acta Petrolei Sinica, 2014, 35(2): 303-309. DOI:10.7623/syxb201402010 |
| [22] | Easley G, Labate D, Lim W Q. Sparse Directional Image Representations Using the Discrete Shearlet Transform[J]. Applied and Computational Harmonic Analysis, 2008, 25(1): 25-46. DOI:10.1016/j.acha.2007.09.003 |
| [23] | Yi S, Labate D, Easley G R, et al. A Shearlet App-roach to Edge Analysis and Detection[J]. IEEE Transcations on Image Processing, 2009, 18(5): 929-941. DOI:10.1109/TIP.2009.2013082 |
| [24] |
魏扬, 那彦, 邓昆明. 基于多尺度几何分析的医学图像融合[J].
电子科技, 2014, 27(8): 19-21.
Wei Yang, Na Yan, Deng Kunming. Medical Image Fusion Based on Multiscale Geometric Analysis[J]. Electronic Science and Technology, 2014, 27(8): 19-21. |
| [25] |
朱华生, 徐晨光. Shearlet变换域自适应图像去噪算法[J].
激光与红外, 2012, 42(7): 811-814.
Zhu Huasheng, Xu Chenguang. Adaptive Image Denoising Algorithm Based on Shearlet Transform[J]. Laser & Infrared, 2012, 42(7): 811-814. |
| [26] |
胡海智, 孙辉, 邓承志, 等. 基于Shearlet变换的图像去噪算法[J].
计算机应用, 2010(6): 1562-1564.
Hu Haizhi, Sun Hui, Deng Chengzhi, et al. Image De-Noising Algorithm Based on Shearlet Transform[J]. Journal of Computer Applications, 2010(6): 1562-1564. |
| [27] |
刘成明, 王德利, 王通, 等. 基于Shearlet变换的地震随机噪声压制[J].
石油学报, 2014, 35(4): 692-699.
Liu Chengming, Wang Deli, Wang Tong, et al. Random Seismic Noise Attenuation Based on the Shearlet Transform[J]. Actc Petrolei Sinica, 2014, 35(4): 692-699. DOI:10.7623/syxb201404009 |
| [28] |
刘成明, 王德利, 胡斌, 等. Shearlet域稀疏约束地震数据重建[J].
吉林大学学报(地球科学版), 2016, 46(6): 1855-1864.
Liu Chengming, Wang Deli, Hu Bin, et al. Seismic Data Interpolation Based on Sparse Constraint in Shearlet Domain[J]. Journal of Jilin Universityv(Earth Science Edition), 2016, 46(6): 1855-1864. |
| [29] | Kittipoom P, Kutyniok G, Wang Q L. Construction of Compactly Supported Shearlet Fremes[J]. Constructive Approximation, 2012, 35(1): 21-27. DOI:10.1007/s00365-011-9142-y |



