0 引言
磁电法是测量两点间由人工源非感应(直流或者伪直流)电流激发的磁场、而非电位差的一类电磁勘探方法体系。国外学者将此方法体系统称为磁电法(MMR)[1],广义上包括直接观测磁场各分量的磁测法、观测激发极化效应产生二次场的磁激发极化法(MIP),以及观测磁场总场的亚音频磁测法(SAM),狭义上则特指第一种方法。国内学者为了便于区分,将各种方法统称为磁电法[2-3],本文也采用同样的命名方式。磁电法观测到的磁异常是由地层中的传导电流引起的,通过对磁异常的分析确定地质靶体的导电性和电化学作用。磁电法按应用领域可以分为地面磁电法、井中磁电法和海洋磁电法。MMR是磁电法中最主要的方法,在各领域都有应用;MIP和SAM主要在地面测量应用较多,海洋和井中测量应用较少。磁电法地面测量时受导电覆盖层影响较小,且测量中可以不用接地,受沙漠、沼泽和冰川等复杂地质条件影响小,测量速度较快,不仅被应用在传统的地质调查和找矿领域,近年来在工程勘察和污染物监测等领域也取得了良好的应用效果,并且在井中测量时对深部目标体也有较好的反映。海洋磁电法在探测深海洋壳电性结构中有成熟的应用。国内于20世纪70年代末开始磁电法的研究,但是总体来讲应用较少,究其原因,一方面源于磁电法一些本身的局限性,另一方面也源于其他电磁方法的快速发展。虽然磁电法存在一定的局限性,但在特定条件下优势也十分明显。在传统方法应用效果不好的地区,根据特定的地质条件与找矿目标来选用例如磁电法这种特点明显的勘探方法,会收到较好的效果。同时,随着仪器精度水平的大幅提高,正反演算法也得到了突飞猛进的发展,磁电法所受技术上的局限已经越来越小,其方法上的优越性更加凸显,应用范围由地面拓展到井中和海洋,特别在环境和工程地球物理勘探中焕发出了新的活力。
本文首先介绍磁电法统一的控制微分方程,从数据采集与分析、正反演理论以及应用现状等3个方面讨论地面磁电法、井中磁电法和海洋磁电法在国内外的发展历程与最新进展,进而阐述磁电法的优势与局限性;然后根据国内外不同领域的应用实例,分析实际应用中的优缺点;最后对磁电法技术的发展做出展望,为此方法在我国的推广与应用提供帮助。
1 磁电法控制方程在磁电法模拟中,通常假定发射源为直流源,所以在进行控制方程的推导时将麦克斯韦方程的频率设为0[4],即
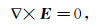 (1a)
(1a) 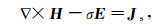 (1b)
(1b) 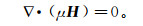 (1c)
(1c) 其中:E是电场强度;H是磁场强度;Js是场源电流密度;σ和μ分别是电导率和磁导率。由式(1a)可见,存在一个标量电势φ,满足
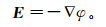 (2)
(2) 与式(1b)相结合并取散度,可以得到直流方程:
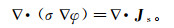 (3)
(3) 通过适当的边界条件,可以由式(3)解得φ。这样我们可以得到如下关于H的方程:
 (4)
(4) 其中:f是源项,满足∇·f=0。式(4)、式(1c)和边界条件一起定义了静磁场问题[5-6]。
为了方便求解静磁场问题,根据式(1c),引入磁场势A,满足
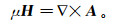 (5)
(5) 将式(1c)和式(4)合并,在适当的边界条件下可得
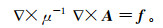 (6)
(6) 有学者在此基础上添加了稳定算子∇×μ-1∇·A来确保方程的正定性[7]:
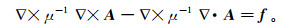 (7)
(7) 其中,A满足库仑规范条件∇·A=0。为了在电导率和磁导率高度不连续的情况下依然能够得到较高的精度,引入变量ψ,满足
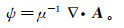 (8)
(8) 这样可以得到关于(A,H,ψ)的控制方程[4]:
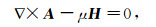 (9a)
(9a) 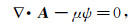 (9b)
(9b) 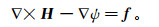 (9c)
(9c) 同时式(3)也能够分解成关于(J,φ)的控制方程[4]:
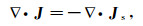 (10a)
(10a) 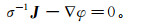 (10b)
(10b) 无论磁电法的应用领域是在地面、井中还是海洋,都是基于对于控制方程(9)或者(10)的求解[1, 4, 8], 差别在于发射源和接收器的位置与数量, 在下文会具体讨论。
2 磁电法数据采集与分析本节主要从地面、井中和海洋3个应用领域对磁电法的工区布置、仪器设备和数据分析等进行介绍。
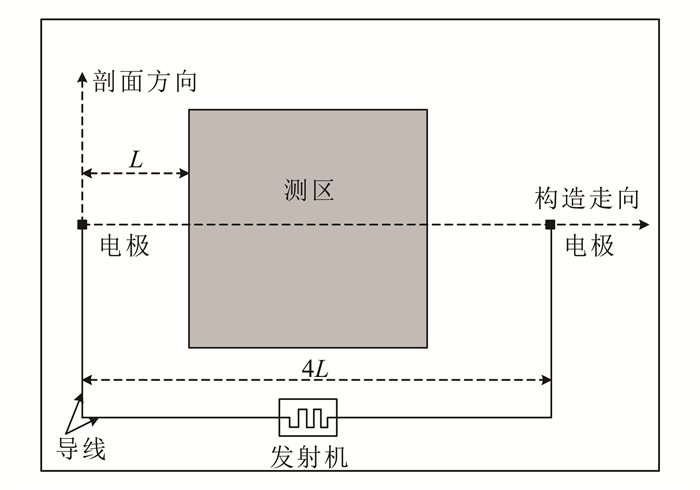
2.1 地面磁电法 2.1.1 数据采集技术地面磁电法通常采用中梯方式观测,发射导线成马蹄铁型绕开测区(图 1),这样可以减小源导线中电流激发的磁场Bw对测区的干扰[4, 10]。观测数据为电流源激发的一次磁场各分量(MMR),也可以通过观测二次磁场求取视极化率(MIP)[11]。Cattach等[12]提出的亚音频磁测技术可以同时测量磁场和电场。在SAM观测中,会得到高清晰度磁法(HDM)、总场磁电法(TFMMR)、总场磁激发极化法(TFMIP)和总场电磁法(TFEM)数据。其中TFMMR/TFMIP和传统的MMR/MIP相比最大的区别在于测量的是总磁场强度而不是磁场的各个分量[13]。
磁电法的信号强度较弱,通常只有几纳特,如果是测量二次场则信号更小,一般只有几十皮特[14], 所以对仪器设备精度要求较高。为了获得更大的场源信号,发射机一般采用激发极化法(IP)中使用的大功率发射机。接收仪器则采用精度较高的磁测仪。最新由Willowstick技术公司研发的三分量磁测仪具有抗干扰能力强、便携式等特点,一个测点的测量时间仅需2~4 min,且可以同步定位[15]。
2.1.2 测区磁场数据在地面磁电法测量中,观测到的总磁场Bobs分为2个部分,即地层中电流激发的磁场Bg和源导线中电流激发的磁场Bw:
 (11)
(11) 其中,Bw可由毕奥-萨伐尔定律算得解析解[16]:
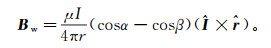 (12)
(12) 式中:I为电流振幅;r为收发距;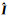
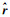
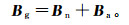 (13)
(13) 其中:Bn是背景磁场;Ba是由电流密度扰动引起的异常磁场。需要注意的是,Bn是水平的,而且对于地面测量来说,一维层状介质和均匀半空间产生的Bn是相同的,其场值只与I和r有关[17]:
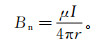 (14)
(14) 由此可见,观测信号中只有Ba与异常场有关。要注意的是,一般所指的磁电异常Ma是由异常场对测区中心点处的背景场Bn0场值归一化得到的百分比[4, 14],即:
 (15)
(15) 与MMR相比,SAM观测到的总磁场场值BT多了一部分随空间变化的磁场场值Bs[9]:
 (16)
(16) 式中,Bmod是由发射机产生的低频调制信号场值,等同于MMR测量中观测的总磁场Bobs的场值。Bs和Bmod在谱上有明显的分别,可由滤波器分开。
当存在地形影响时,可先对含地形的观测数据Bobst进行地形校正[18-19]:
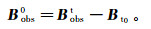 (17)
(17) 其中:Bobs0是经过地形校正后的磁异常;Bt0是带地形的均匀半空间产生的磁场值。
各个分量中,y分量(以场源走向为x方向)是正反演效果最好的分量[4]。原因如下:从总场场值来讲,Bobsz > Bobsy > Bobsx,从异常场场值来讲,Baz≈Bay > Bax;但在实际测量中导线很难保证是直的,而且可能受地形的影响,所以z分量的噪音水平要大于y分量。综上所述,y分量通常是信噪比最大的分量。
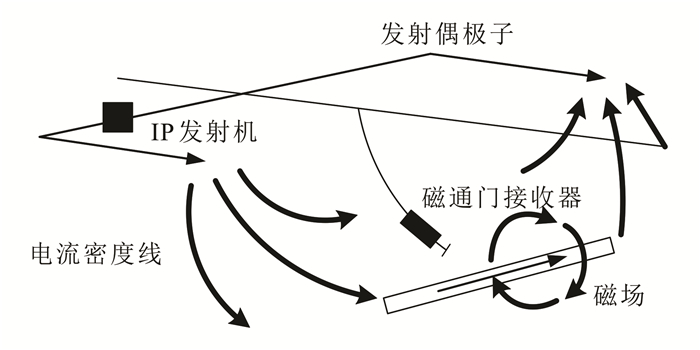
2.2 井中磁电法 2.2.1 数据采集技术井中磁电法(DHMMR)的测区布置与地面磁电法相同(图 2),不同之处在于发射或者接收装置是在井中,可以分为单个井孔发射接收、不同井孔(跨孔)发射接收、地面发射井中接收和井中发射地面接收4类观测系统[20]。
DHMMR的数据采集中探头是关键。传统的磁场探头无法在测量较低磁场信号的情况下保持较高的信噪比,并且尺寸也不满足标准的矿产勘查钻孔(通常为40 mm直径)[21]。所以早期DHMMR探测均采用瞬变电磁(TEM)探头接收磁场信号[22-23]。但是采用TEM探头有2个限制:首先是TEM探头测量的是∂B/∂t而不是直接测量磁场,为了达到DHMMR的要求,需要进行数据处理;其次,TEM探头原本适用于发射频率为1~2 kHz的TEM发射源,而对于低频的DHMMR发射源,其受背景噪音的影响比较明显。为了解决以上的问题,澳大利亚莫纳什大学及其赞助商研发了MAGPI探头,是一种适用于井中直接测量磁场三分量的高信噪比探头[21, 24]。在此基础上形成了一整套井中MMR系统,实现了井中磁电阻率数据相位和振幅的同步测量[25-26]。
2.2.2 井中数据与地面数据的区别DHMMR的数据处理过程与地面磁电法相似,最大的优势在于可以区分层状介质和均匀半空间。在层状介质中,异常磁场场值
 (18)
(18) 其中:λ为波数;σ1和σ2分别为源点上下两层介质的电导率;h1为电极埋深。由式(18)可见:当测点位于地表时(z=0),异常场为零,此时地面磁电法数据无法区分层状介质和均匀半空间;当测点位于地下(z < 0),即井中勘探时,异常磁场值与深度相关,这是地面磁电法和井中磁电法根本性的区别。
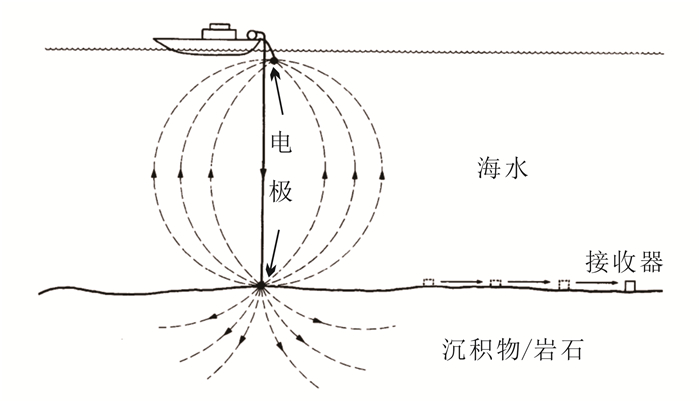
2.3 海洋磁电法 2.3.1 数据采集技术在进行传统的海洋可控源勘探时,发射器被船拖拽,位于海水深处,仅高于海底几十米。因为海底存在地形起伏,如何始终保持发射器与海底间适当的距离间隔是一个技术难题。海洋磁电法将电极悬挂在船的一边作为垂直电偶源,从而回避了这样的问题。图 3所示为用于海洋磁电法的MOSES(magnetometric offshore electrical sounding)系统[29],Edwards等[30-31]系统阐述了其原理。图 4为典型的海洋磁电法施工示意图。MOSES系统的发射源为由海平面到海底的垂直长导线。2个供电电极一个位于海平面,另一个位于海底。接收器OBM(ocean bottom magnetometer)被固定在海底,由2个水平正交的磁场探测器组成。但是MOSES装置同样存在缺陷,发射偶极天线会受水流影响而偏向一侧,在每次发射之前需要一段时间将天线复位回到垂直位置。而传统的深部拖拽式海洋可控源发射系统是可以连续发射的,这样在相同的时间内海洋磁电法所得到的数据要少[33]。为了解决这样的问题,Seama等[34]开发了可连续拖拽的垂直偶极子海洋磁电法发射系统,在中马里亚纳海沟进行的浅部海洋地壳电阻率结构探测中表明,此发射系统可以有效减少勘探时间并提高分辨率。
2.3.2 视电阻率计算海洋磁电法测得的数据为2个水平磁场分量,通常将其转化为视电阻率,计算公式主要有3种。
第一种由Edwards等[30]和Chave等[35]提出:
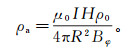 (19)
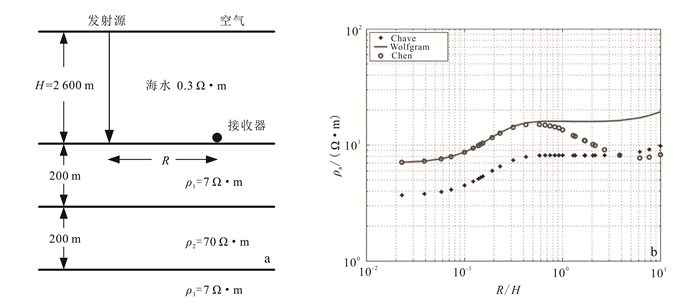
(19) 其中:ρa为海底电阻率;Bφ是接收器中测得的方位角磁场;R是接收器与发射导线之间的径向距离;I为发射线源电流;μ0是真空磁导率;H为海水深度;ρ0是海水电阻率,是假定已知的。公式(19)成立需满足1 < R/H < ρa/ρ0,试验证明公式(19)在浅海区域是有效的[29];但是当R/H∈(0.1, 0.3)时,即深水区,公式(19)的效果并不好(图 5)。
Wolfgram等[37]提出了第二种视电阻率的计算方法:
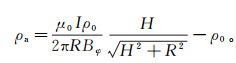 (20)
(20) 公式(20)忽略了海平面上电极的影响,假设顶电极的位置在无限远处,其成立的条件是收发距必须小于海水深度(即R < H),可见在浅水区并不适用;不过其在深水区的效果相对于Chave公式已经有明显提高(图 5)。
Chen等[36, 38]考虑了发射导线和接收器之间的几何差异,导出了新的视电阻率公式:
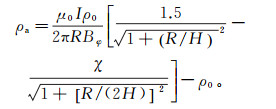 (21)
(21) 其中,
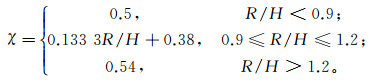
公式(21)不仅可以应用于浅海,而且可以应用在深海磁电法探测中,效果要好于Chave公式和Wolfgram公式(图 5)。Yooyuanyong[39]应用公式(21)构造了MMR数据反演的初始电导率模型。
3 磁电法正反演理论 3.1 磁电法正演理论磁电法的正演计算早期主要有3种方法。首先是关于简单地电结构的解析解。Edwards等[40]总结了层状介质中球体、各向异性球体、不同电阻率垂直和倾斜接触面、厚度不同的垂直矿脉以及半圆柱体和半球体的解析解表达式。Sezginer等[41]用镜像法计算均匀半空间中任意电流激发的静态磁场。Inayat-Hussein[42-43]在此基础上用傅里叶级数积分计算水平层状介质中圆柱体由直流电源激发的磁场。
第二种方法是曲面积分方程法。对于简单问题来说,异常体除了表面电导率的变化外,其他位置处电导率的梯度全都为0。因此,可以将修正的毕奥-萨伐尔定律的体积分分解为一组有限的面积分集合。基于这种思想,Gómez-Treviño等[44]推导了一种在二维结构中计算磁场三分量的快速算法。Nabighian等[45]及Cheesman等[46]模拟了多重有限平板任意电阻率的MMR异常。Hvoždara等[47]用边界积分计算了垂直接触面附近三维异常体的MMR响应。Méndez-Delgado等[48]用积分方程法对包括MMR在内的直流和低频电磁场进行了三维正演模拟。
第三种方法基于直流电法正演问题[17]。首先用有限差分或者有限元方法求解关于电势场的泊松方程,接下来通过修正的毕奥-萨伐尔定律计算磁场[40]:
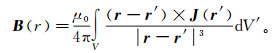 (22)
(22) 式中:J是电流密度元;r是测点位置;r′是电流密度元位置;V′是电流密度元的体积。Acosta等[22]、Pai等[49]、McGillivray[50]以及Yang等[51]在此基础上计算了二维模型的MMR响应。Boggs等[52-53]用有限差分法在傅里叶域中对三维地电结构的TFMMR响应进行了探讨。Fathianpour等[9]在此基础上对TFMMR进行了2.5维有限元模拟。
2000年以后,随着电磁理论的发展,学者们多将磁电法正演模拟认为是静电场和静磁场的混合子问题:首先通过标量电势解决直流电阻率问题,并通过电流密度源解决静磁场方程;然后由静电场的麦克斯韦方程组出发,得到控制方程(具体推导见本文第1节);之后采用不同的数值方法对控制方程求解,例如有限元法[5-6]和有限体积法[1, 4, 54],将磁电法的正演模拟带入了三维阶段。Yooyuanyong等[55-56]从麦克斯韦方程组出发,对电导率不均匀层状介质的磁场进行求解,地层的电导率随深度以指数倍变化,即σ(z)=ae(bz),其中a和b是定义电导率剖面的参数。随后,Chaladgarn等[57]又用这种方法计算了覆盖层下导电围岩的磁电阻率响应。Butler等[58]采用多物理场耦合分析软件(comsol multiphysics)中的AC/DC模块对包括MMR在内的多种电法方法进行正演模拟,其原理也是由麦克斯韦方程组出发解决电磁问题。Comsol Multiphysics作为商业化的有限元软件包,其优势在于用户可以通过软件界面进行简单操作即可实现复杂模型的构建,并且可以对同一个模型的多种物理场效应进行综合研究。
3.2 磁电法反演理论 3.2.1 磁电法常用反演技术相对于正演模拟,磁电法的反演技术进展比较缓慢。早期有学者用典型曲线对一些简单的二维目标体进行定性分析[59],通过重力数据和磁电阻率数据之间的相似性用试错法在实验室中进行物理模拟,从而进行三维数据解释[60]。Asten[16]也利用这种相似性,采用标准二维重力模拟方法处理井中磁电阻率数据。Hishime等[61]根据典型曲线定性解释MIP的实测数据。但是Bishop等[62]指出标准的重力算法通常假设地面导线是平坦的,并不适用于偏离井孔的勘探。Sripanya[63-64]用Levenberg-Marquardt最优化方法对电导率随指数变化的地层进行了反演,随后又用正则化共轭梯度法对层状地层进行了反演,并用L曲线准则确定合适的正则化参数。
Chen等[4]采用正则化的反演思想率先实现了对磁电阻率数据的三维反演,目标函数求解采用共轭梯度最小二乘方法(CGLS)。LaBrecque等[65]采用Occam方法联合反演由同一低频源激发的高密度电阻率成像法(ERT)和MMR数据。除此之外,还有用马夸特反演方法进行二维反演的成功例子[10]。Chen等[4]和LaBrecque等[65]所采用的Occam反演的主要区别在于正则化项。Chen等[4]是将反演模型相对初始模型的加权偏差作为正则化项;而LaBrecque等[65]是采用粗糙度作为正则化项。Chen等[66]用共轭梯度最小二乘法进行了MIP的三维反演研究。Bouchedda等[1]采用非线性迭代最小二乘正则化技术,对目标函数的最小化采用Gauss-Newton算法,实现了井中磁电法数据的三维反演。
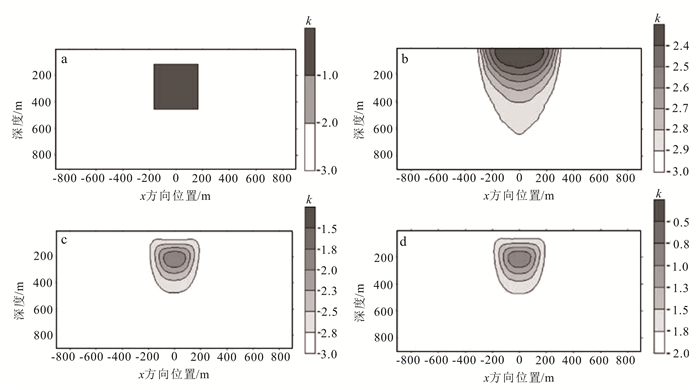
3.2.2 磁电法反演中的问题磁电法数据反演中会遇到2个问题。首先是地面数据对于异常体的深度分辨能力不足。对于地面磁电法反演深部异常体,其反演的结果主要集中在地面,相对于横向分辨率,纵向分辨率较差,如图 6所示。在磁电法二、三维反演中都遇到了这样的问题[4, 60]。
众所周知,作为静态位场,重力场并没有固有的深度分辨能力[67],基于静磁场与重力场数学上的相似性,地面磁电法数据的深度分辨能力同样不好[4]。早期学者主要采用2种方法来解决磁场的分辨率问题。第一种方法就是仿照重力场反演,将地下介质分成许多大小固定但是磁化率未知的单元,通过对模型目标函数的最小化产生一个简单模型来拟合数据,但是仅适用于反演一些简单的异常体[68-70]。第二种办法是进行参数化反演,通过对几个几何形状简单异常体的参数或者其磁场值的傅里叶变换来进行非线性反演,再用它们的值来解决磁场数据反演这样的超定问题。这种方法对于由简单异常体引起的异常是合适的,但是需要关于源的大量先验信息以完成初始参数化,而且在考虑磁导率时会受到限制[71-73]。
为了不仅拟合数据,并且与其他可行的模型约束相吻合,Li等[74]对磁场数据的目标函数进行加权反演,引入了权函数来抵消核函数的几何扩散并且提高深部密度分辨率。随后他们又在对重力场数据反演时运用了相同的方法,并详细解释了如何加权[67];这种方法又推广到地面磁场数据和井中磁场数据的联合反演当中[75]。Chen等[4]根据静磁场与重力场的相似关系,将同样的深度加权方法引入到地面磁电法数据反演中,其权函数与Li等[74]对磁场数据进行三维反演时应用的类似。图 6为采用加权方法的反演结果示意图。由图 6可见,经过加权之后的反演结果明显向深部移动,并且电导率之比也与真实情况更加吻合。Zhdanov[76]在对重磁数据进行正则化反演时也采用对模型修正量加权的方法来解决位场深度分辨率不足的问题,与Li等[67, 74-75]采用的方法相比,差别在于权函数的不同。
磁电法数据反演遇到的第二个问题是地面磁场数据只与介质间的电导率之比有关。也就是说,不同的介质之间,只要其电导率之比相同,其产生的磁场就相同,这样的结果在解析解[40]和数值解[4, 27]中都得到了证实。不同的均匀半空间初始模型对于反演结果没有影响(图 6c、d),目前还没有解决的方法。
4 国内外磁电法应用现状 4.1 地面磁电法MMR最早的应用就是在地面勘探,在1933年由Jakosky[77]在一项专利中提出,他认为可以在野外勘探中通过对磁异常的分析而达到勘探目的,但是限于当时仪器设备的落后和理论基础的不完备,该方法在当时并没有引人注意。随着仪器设备的不断进步,人们渐渐认识到了MMR的优势,基础理论也逐渐完备。其最早被应用于圈定起伏地形下不同电阻率基岩之间的断层接触[78-79]。后来,地面磁电法逐渐被应用于矿产资源勘查,近年来在环境与工程领域又有新的应用。
4.1.1 地面磁电法在矿产资源勘查中的应用磁电法在矿产勘查中主要有3个优势。第一,因为磁电法只对其目标体和背景之间的相对电阻率敏感,而不是绝对电阻率,所以对于寻找那些导电性较差的目标体。例如石墨矿和闪锌矿等,只要其与背景电阻率存在差异,磁电法的效果就比较明显。第二,磁电法受低阻覆盖层的影响较小。例如,一个导电性地质靶体位于1 000 Ω·m的背景电阻率中,当其上覆盖30 m厚、电阻率为100 Ω·m的覆盖层时,对于直流电法来说,异常体的信号将被十分明显地削弱;然而对于磁电法来讲,与没有覆盖层时相比,其信号只被减少了约10%[4]。第三,地面磁电法测量时不需要接地,在一个测点上消耗的时间较少,可以用来进行快速普查,在接地条件不好的地区(冻土地带、干燥的沙漠或者冰层等)具有巨大的优势, 而且避免了电极与大地之间因电化学作用不稳定所造成的影响。
基于以上3个优势,磁电法在矿产勘查领域取得了不错的应用效果。Seigel[80]首先采用MIP寻找块状侵染硫化物和石墨矿。随后学者们陆续在澳大利亚和加拿大等11处不同的金属矿区进行了时间域和频率域的MIP勘测,当存在盐湖或风化岩石覆盖层时,也能够区分硫化物矿床以及石墨矿床[59, 81]。MIP可作为电激发极化法(EIP)的有效辅助手段,在相同的勘探效果下花费较少[61]。Chen等[4]在澳大利亚的Mons氢氧化铜矿区进行地面磁电法勘查,成功刻画出铜矿化体的体积。Chen等[66]在澳大利亚的Binduli矿区进行首次三维MIP反演研究,对高导电覆盖层下的金矿勘探取得了良好的效果。近些年来,地面磁电法测量多采用SAM方法,可以实现多种电磁方法的同步测量。Fathianpour等[10]将TFMMR成功应用于澳大利亚Flying Doctor矿区的铅银锌矿的勘探。德国科廷科技大学以及多家公司在西澳大利亚3个矿区采用SAM方法进行了一系列的勘测:在Woodie地区圈定了浅层导电锰矿的范围[82];在Songvang金矿成功区分出风化层和矿化带[83];在St Ives矿区通过SAM方法与多种勘探方法相结合详细研究了超盐性环境下风化层的地球物理响应[84]。Southern Geoscience、Saracen Mineral和Gap Geophysica Australia等3家公司在西澳大利亚的Far South矿区通过SAM准确识别了块状硫化物目标[85]。经过多年的生产实践,磁电法被证明在寻找火山岩类块状硫化物矿床(VMS)、斑岩铜矿床(PCDs)和花岗岩-绿岩带金矿床等具有良好的效果[86]。
随着研究的不断深入,磁电法体现出越来越多的优势,但其依然不是矿产勘探中的常规方法。主要有3个问题阻碍磁电法的发展。首先是MMR异常的信号普遍较低,MIP异常更弱,对仪器设备的要求较高。其次是观测结果的复杂性较高,x、y和z三个分量与目标体的几何结构之间没有简单的对应关系,异常形态各不相同[4]。第三,地面磁场数据是独立于地层电导率的,不利于区分地层[42-43]。
4.1.2 地面磁电法在水文、环境和工程领域的应用传统地球物理方法想要高精度描绘地下水系统是比较困难的,地表的地质调查很难确定地下含水通道的位置[87]。地面磁电法可快速、精确地确定地下水运移通道。Street[88]首先将MMR应用于西澳大利亚Eastern Goldfields地区的古河道定位。Goldman等[89]在地下水勘探的可行性研究中表明,MMR和时间域电磁法(TDEM)相结合对于地下水的分布和水量的探查在技术和原理上是最适合的。Kulessa等[90]在实验室环境下首先引入MMR来判断地下水中溶质的迁移情况,LaBrecque等[91]首先将MMR与电阻率层析成像技术(ERT)相结合,在工程勘探中探查浅层的三维结构有良好的效果[65]。Willowstick技术公司通过MMR对地下水的流向进行精确模拟,在水坝、矿山、环境监测点以及垃圾沥滤场等地球物理调查中起到了关键的作用[15, 92]。Maxwell等[93]将MMR与ERT结合来寻找水坝、堤防的渗漏点。MMR结合时延反演技术[94],可对地下水或气体等进行动态监控。采用这种方法,Zhu等[95-96]通过实验室仿真模拟验证了MMR在地下水污染物运移监测中的有效性。
4.2 井中磁电法20世纪80年代,磁电法(主要是MMR)的应用被拓展到井中。与地面磁电法一样,DHMMR主要应用于矿产资源勘查,在水文、地热、环境和工程领域也有所应用。
4.2.1 井中磁电法在矿产资源勘查中的应用Nabighian等[45]采用跨孔装置,在超过500 m深度下成功圈定了块状硫化物矿化带。Asten[16]采用地面发射井中接收和单孔发射接收的方式,在澳大利亚昆士兰Dreghorn和Thalanga两处矿床成功圈定了铜铅锌矿化带。Veitch等[97]指出磁场分量能够清楚分辨电导率分界面,得知目标体距离井孔的位置和方向,与电势剖面相比是一个优势。Bishop等[62]采用DHMMR在澳大利亚新南威尔士的Broken Hill寻找闪锌矿取得较好的效果, 矿床深度超过600 m, 与井孔距离超过150 m。DHMMR又被应用于超出风化层下100 m深的镍硫化物矿床[98]和深度超过500 m的金矿床勘探[99]。有学者采用MAGPI探头在Broken Hill地区勘探条带状闪锌矿时取得了良好的效果[100-101]。Bouchedda等[1]进行了首次DHMMR三维反演研究,成功在爱尔兰的Tobermalug地区地下375 m处定位了细长的铜铅锌矿化带。
由以上实例可见,DHMMR与地面磁电法一样,对弱导电体有较好的反映[102],优势在于勘探深度大大增加[103],为地球物理和地质之间建立了一个有效的联系[104]。与TEM测井相比,DHMMR对目标体形状和方向的判断更好,且测量更加快速[105];但是电导率的分辨率略逊一筹,可以作为TEM测井的补充方法[106]。
4.2.2 井中磁电法在地热、环境和工程领域的应用DHMMR第一次成功的应用就是在环境工程领域中,在采石场下方50 m深度成功地确定了垃圾填埋沥液随岩石裂隙流动的方向和区域[22]。Labrecque等[107]对井地和跨孔2种排列方式进行模拟实验,确定DHMMR可以用来探测地热环境中的裂隙。Fielitz等[108-109]进行了浅层二维跨孔MMR实验,清晰反映了地表 20m内的层状结构,为工程领域内的应用奠定了基础。Bouchedda等[110]通过对DHMMR数据的三维模拟,定量检测深层盐水层中地质封存CO2的含量,并判断其运移方向。
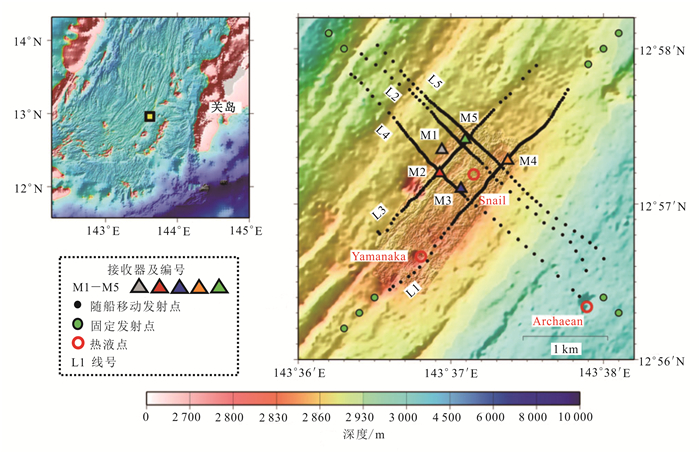
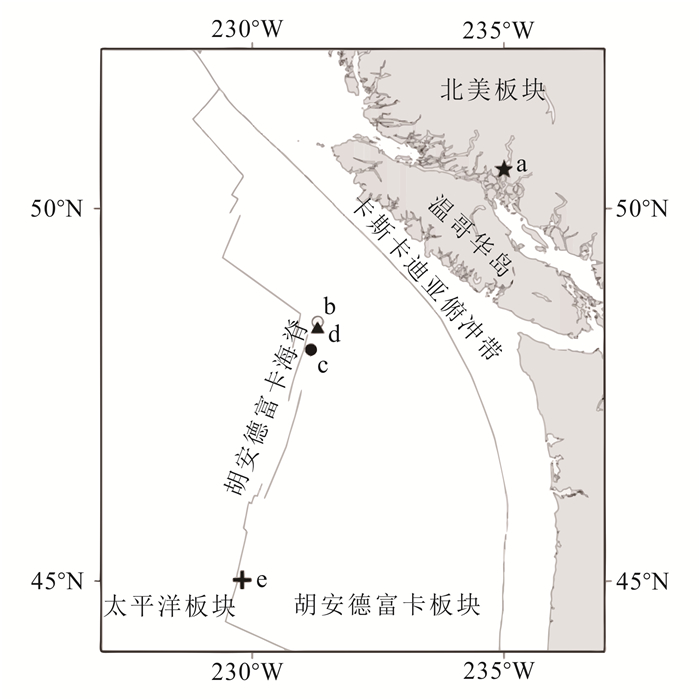
4.3 海洋磁电法相对于地面和井中,MMR在海洋勘探中更被人们所熟识。低频电流(DC)方法对于海底的电阻区并不十分敏感,海洋磁电法的优势在于区分海底高低阻区[32]。1985年,MOSES系统进行了首次实验, 在相对高阻基底之上成功划分出沉积层[32],随后此装置在一系列深海区进行了应用(图 7和表 1),成功测定了洋脊附近的地壳结构。同时,在100 m以下的浅海地区也成功进行了永久冻土区电性调查[116]。与电阻率法相结合,对于热液环流产生的地电响应也有较好的反映[117]。
| 时间及工区位置 | 平均海水深度/m | 源电流/A | 发射站数目 | 接收器数目 |
| 1985,不列颠哥伦比亚,比特湾[29](图 7a) | 640 | 25 | 14 | 1 |
| 1986,胡安德富卡海脊北部,中央谷地[112](图 7b、7c) | 2 500 | 20 | 31 | 3 |
| 1992,胡安德富卡海脊北部,中央谷地[113](图 7d) | 2 400 | 20 | 55 | 6 |
| 1998,胡安德富卡海脊,克莱夫特—万斯超覆盖扩张中心[114](图 7e) | 2 300 | 15 | 34 | 3 |
| 2002,东太平洋海隆,9°50′N[115] | 2 550 | 13 | 200 | 10 |
| 2005,马里亚纳海沟中部,18°13′N[111] | 3 600 | 19 | 35 | 4 |
| 2015,马里亚纳海沟南部[32](图 4) | 1 500 | 16 | 250 | 5 |
目前的海洋磁电法研究多采用一维电阻率结构,这是由海洋勘探中的实际因素所决定的。因为发射源比接收装置数量多,所以每一个发射源需要独立解决麦克斯韦方程组,这使得实现海洋磁电法数据的三维正反演比较困难。Chen等[8]提出2种方法去解决这样的问题:第一种方法是基于洛伦兹互易定理,接收器处测得的由垂直电偶极源激发的磁场与发射导线中由接收器位置人工磁偶极子生成的归一化感应电动势是相同的;第二种方法是伴随法,可以通过求解每一个接收器位置人工源的伴随方程来得到磁场。Chen等[8]认为这2种方法在本质上是相同的,都是以观测系统中的稳定电流作为人工源,“测量”的都是沿发射导线的电压,但是伴随方法的计算效率更高,Chen等[8]采用这种方法进行三维海洋磁电法正演模拟。此外,Matsuno等[32]通过观测数据与一维最优化电阻率结构之间的差值得到磁场异常,将磁异常通过三维正演得到马里亚纳海沟南部洋壳的三维电阻率结构。综上所述,一系列的发展使得MMR与大地电磁(MT)、地磁测深(GDS)和可控源电磁法(CSEM)一道成为探测海底电阻率结构的标准方法之一[118]。
4.4 国内磁电法的发展现状及应用国内对于磁电法的研究始于20世纪70年代末,最先引起国内学者注意的是MIP方法[119]。励宝恒等[120]综合了加拿大先得利公司已经发表的专利及资料,对MIP的基本原理及地质效果做了简要介绍。傅良魁[121]计算了水平圆柱体MMR和MIP的理论剖面曲线,在侵染型铜矿上进行了野外实测,指出磁电法在寻找长走向的良导性矿体和极化体方面较为有利。崔焕敏等[122]较早地在野外工作中对磁电法进行实践,总结出了一套实际工作的流程。傅良魁[2]出版了目前唯一一本关于磁电法的中文专著,对MMR和MIP的理论进行了一系列研究,介绍了一些实验结果和野外实例。张书成[123]介绍了MMR在国内矿床上的应用情况,举例说明了该方法用于找矿和找断裂构造的效果。杨建文等[124-126]对起伏地形下MMR的一维正演以及资料处理进行了一系列研究,提出了与Oppliger不同的地形校正公式。台湾学者杨洁豪等[51]讨论了MMR模拟时的地形响应问题。邓靖武[3]在国内首先用有限差分方法实现了三维磁电法正演,根据数值模拟结果讨论了高、低阻屏蔽层的影响以及如何区分组合异常体。朱凯光等[95-96]首次在国内将MMR应用到环境领域。翁爱华等[127]基于对层状介质的垂直磁场响应的计算研究了天然气水合物的磁电阻率响应。中国地质科学院地球物理地球化学勘查研究所采用列阵电磁接收系统与大功率发射机[128-129],进行了MIP方法技术试验研究[14, 130]。综上所述,在方法上,国内磁电法的研究集中在MMR和MIP,SAM还未见报道;在应用领域主要集中在地面找矿,近些年来有环境和工程物探的研究,但是井中和海洋中的研究相对很少。
5 结论与展望目前,我国较易勘探的陆地浅部资源勘查基本完成,勘查目标转向地质条件较差的地区和地球深部以及海洋;而且,在勘探的过程中既讲经济效益,又强调减小对环境的影响。磁电法可以在地面、井中和海洋完成勘探任务,测量较快,测量装置不接地,是适于我国现阶段发展需求的一种勘探方法。
对于我国磁电法的研究与应用有以下4个展望:
1) 数据采集。传统的地面采集方式为马蹄形布线,可以尝试其他应用成熟的电磁法观测方式,甚至多源观测,实现矢量甚至张量测量。因为不用接地,可以将磁电法测量装置与车辆甚至飞行器相结合,开展航空磁电法研究。
2) 正演。因为从静电场理论出发无法得到绝对的电导率值,可以尝试借鉴其他方法解决正演问题,例如从麦克斯韦方程组出发。可以通过引入三维有限元方法来解决带地形的正演问题。
3) 反演。地面数据深度分辨能力不足的问题需要反演时更好的解决方案。因为采用低频(近直流)发射源,多源多分量三维反演相对于感应电磁法更易实现。
4) 应用的领域。相对于国外得到充分发展的井中磁电法和海洋磁电法,国内几乎无人涉猎。井中磁电法可以解决地面磁电法对于深部分辨能力不足的问题。海洋磁电法已经被证实可以在探查洋壳电性结构上有突出的效果,可以用来确定热液环流的范围和类型。我国已经初步具备了在深海中进行海洋资源调查的能力[131],海洋磁电法在我国的发展前景大有可为。在环境与工程领域磁电法已经被证明有良好的应用效果,在国内可以借鉴采用。
| [1] | Bouchedda A, Giroux B, Glencor M A. Down-Hole Magnetometric Resistivity Inversion for Zinc and Lead Lenses Localization at Tobermalug, County Limerick, Irland[C]//2015 SEG New Orleans Annual Meeting. New Orleans:[s.n.], 2015:2007-2011. |
| [2] |
傅良魁.
磁电勘探法原理[M]. 北京: 地质出版社, 1984.
Fu Liangkui. The Principle of Magnetometric Resistivity Method[M]. Beijing: Geological Publishing House, 1984. |
| [3] |
邓靖武. 磁电法正演理论研究[D]. 北京: 中国地质大学, 2005.
Deng Jingwu. Forward Theory Study of Magnetometric Resistivity and Induced Polarization Methods[D]. Beijing:China University of Geosciences, 2005. http://cdmd.cnki.com.cn/Article/CDMD-11415-2005102519.htm |
| [4] | Chen J, Haber E, Oldenburg D W. Three-Dimensional Numerical Modelling and Inversion of Magnetometric Resistivity Data[J]. Geophys J Int, 2002, 149(3): 679-697. DOI:10.1046/j.1365-246X.2002.01688.x |
| [5] | Haber E. A Mixed Finite Element Method for the So-lution of the Magnetostatic Problem with Highly Discontinuous Coefficients in 3D[J]. Computational Geosciences, 2000, 4(4): 323-336. DOI:10.1023/A:1011540222718 |
| [6] | Jin J. The Finite Element Method in Electromagnetics[M]. New York: Wiley-IEEE Press, 2002. |
| [7] | Haber E, Ascher U M. Fast Finite Volume Modeling of 3D Electromagnetic Problems with Highly Discontinuous Coefficients[J]. SIAM J Sci Comput, 2001, 22(6): 1943-1961. DOI:10.1137/S1064827599360741 |
| [8] | Chen J, Oldenburg D W, Haber E. Reciprocity in Ele-ctromagnetics:Application to Modelling Marine Magnetometric Resistivity Data[J]. Physics of the Earth and Planetary Interiors, 2005, 150(1): 45-61. |
| [9] | Fathianpour N, Heinson G, White A. The Total Field Magnetometric Resistivity (TFMMR) Method:Part Ⅰ:Theory and 2.5D Forward Modeling[J]. Exploration, Geophysics, 2005, 36(2): 181-188. DOI:10.1071/EG05181 |
| [10] | Fathianpour N, Heinson G, White A. The Total Fie-ld Magnetometric Resistivity (TFMMR) Method:Part Ⅱ:2D Resistivity Inversion of Data from the Flying Doctor Deposit, Broken Hill[J]. Australia Exploration Geophysics, 2005, 36(2): 189-197. DOI:10.1071/EG05189 |
| [11] | Howland-Rose A W, Linford G, Pitcher D H, et al. Some Recent Magnetic Induced-Polarization Developments:Part Ⅰ:Theory[J]. Geophysics, 1980, 45(1): 37-54. DOI:10.1190/1.1441038 |
| [12] | Cattach M K, Stanley J M, Lee S J, et al. Sub-Audio Magnetics (SAM):A High Resolution Technique for Simultaneously Mapping Electrical and Magnetic Properties[J]. Exploration Geophysics, 1993, 24(4): 387-400. DOI:10.1071/EG993387 |
| [13] | Fathianpour N, Cattach M K. Analytical Solutions for the Total Field Magnetometric Resistivity (TFMMR) Technique[J]. Exploration Geophysics, 1995, 26(3): 158-166. DOI:10.1071/EG995158 |
| [14] |
李建华, 林品荣, 郭鹏. 磁激电方法技术试验研究[J].
地震地质, 2010, 32(3): 492-499.
Li Jianhua, Lin Pinrong, Guo Peng. A Trial Study of Magnetic Induced Polarization[J]. Seismology and Geology, 2010, 32(3): 492-499. |
| [15] | Kofoed V O, Jessop M L, Wallace M J, et al. Uni-que Applications of MMR to Track Preferential Groundwater Flow Paths in Dams, Mines, Environmental Sites, and Leach Fields[J]. Leading Edge, 2011, 30(2): 192-204. DOI:10.1190/1.3555330 |
| [16] | Asten M W. The Downhole Magnetometric Resistivi-ty (DHMMR) Method[J]. Expl Geophys, 1988, 19(2): 12-16. DOI:10.1071/EG988012 |
| [17] | Edwards R N, Nabighian M N. The Magnetometric Resistivity Method in Electromagnetic Methods in Applied Geophysics:Investigations in Geophysics[J]. Society of Exploration Geophysicists, 1991, 2: 47-104. |
| [18] | Oppliger G L. Three-Dimensional Terrain Effects in Electrical and Magnetometric Resistivity Surveys[D]. Berkeley:University of California, 1982. http://www.osti.gov/scitech/biblio/5532467 |
| [19] | Oppliger G L. Three-Dimensional Terrain Corrections for Mise-à-la-Masse and Magnetometric Resistivity Surveys[J]. Geophysics, 1984, 49(10): 1718-1729. DOI:10.1190/1.1441579 |
| [20] | Spies B R. Electrical and Electromagnetic Borehole Measurements:A Review[J]. Surveys in Geophysics, 1996, 17(4): 517-556. DOI:10.1007/BF01901643 |
| [21] | Purss M B J, Cull J P. B-Field Probes for Downhole Magnetometric Resistivity Surveys[J]. Exploration Geophysics, 2003, 34(4): 233-240. DOI:10.1071/EG03233 |
| [22] | Acosta J E, Worthington M H. A Borehole Mag-netometric Resistivity Experiment[J]. Geophys Prospect, 1983, 31: 800-809. DOI:10.1111/gpr.1983.31.issue-5 |
| [23] | Stolz E M G. Direct Detection of Gold Bearing Structures at St Ives, WA-DHEM vs DHMMR[J]. Exploration Geophysics, 2003, 34(2): 131-136. DOI:10.1071/EG03131 |
| [24] | Elders J A, Asten M W. Minimization of Receiver Noise in Downhole MMR Surveys[C]//SEG Technical Program Expanded Abstracts.[S. l.]:SEG, 2000(1):2484. |
| [25] | Purss M B J, Cull J P, Asten M W. Simultaneous Modelling of the Phase and Amplitude Components of Downhole Magnetometric Resistivity Data[J]. Journal of Applied Geophysics, 2003, 54(1): 1-14. |
| [26] | Elders J A, Asten M W. A Comparison of Receiver Technologies in Borehole MMR and EM Surveys[J]. Geophysical Prospecting, 2004, 52(2): 85-96. DOI:10.1046/j.1365-2478.2003.00406.x |
| [27] | Chen J, Oldenburg D W. Magnetic and Electric Fields of Direct Currents in a Layered Earth (Short Note)[J]. Exploration, Geophysics, 2004, 35(2): 157-163. DOI:10.1071/EG04157 |
| [28] | Edwards N. Marine Controlled Source Electromagne-tics:Principles, Methodologies, Future Commercial Applications[J]. Surveys in Geophysics, 2005, 26(6): 675-700. DOI:10.1007/s10712-005-1830-3 |
| [29] | Edwards R N, Law L K, Wolfgram P A, et al. First Results of the MOSES Experiment:Sea Sediment Conductivity and Thickness Determination, Bute Inlet, British Columbia, by Magnetometric Offshore Electrical Sounding[J]. Geophysics, 1985, 50(1): 153-161. DOI:10.1190/1.1441825 |
| [30] | Edwards R N, Law L K, Delaurier J M. On Mea-suring the Electrical Conductivity of the Oceanic Crust by a Modified Magnetometric Resistivity Method[J]. Journal of Geophysical Research, 1981, 86(B12): 11609-11615. DOI:10.1029/JB086iB12p11609 |
| [31] | Edwards R N, Nobes D C, Gómez-Treviño E. Off-shore Electrical Exploration of Sedimentary Basins:The Efforts of Anisotropy in Horizontally Isotropic, Layered Media[J]. Geophysics, 1984, 49(5): 566-576. DOI:10.1190/1.1441691 |
| [32] | Matsuno T, Kimura M, Seama N. Electrical Resis-tivity Structure of the Snail Site at the Southern Mariana Trough Spreading Center[C]//Subseafloor Biosphere Linked to Hydrothermal Systems.[S. l.]:Springer Japan, 2015:241-251. |
| [33] | Key K. Marine Electromagnetic Studies of Seafloor Resources and Tectonics[J]. Surveys in Geophysics, 2012, 33(1): 135-167. DOI:10.1007/s10712-011-9139-x |
| [34] | Seama N, Tada N, Goto T N, et al. A Continuously Towed Vertical Bipole Source for Marine Magnetometric Resistivity Surveying[J]. Earth Planets & Space, 2013, 65(8): 883-891. |
| [35] | Chave A D, Constable S C, Edwards R N. Electrical Exploration Methods for the Seafloor[C]//Nabighian M N. Electromagnetic Methods in Applied Geophysics:Investigations in geophysics.[S. l.]:SEG, 1991:931-966. |
| [36] | Chen J, Oldenburg D W. A New Formula to Com-pute Apparent Resistivities from Marine Magnetometric Resistivitydata[J]. Geophysics, 2006, 71(3): 73. |
| [37] | Wolfgram P A, Edwards R N, Law L K, et al. Po-lymetallic Sulfide Exploration on the Deep Sea Floor:The Feasibility of the MINI-MOSES Experiment[J]. Geophysics, 1986, 51(9): 1808-1818. DOI:10.1190/1.1442227 |
| [38] | Chen J, Oldenburg D W. Inversion of Marine MMR Data[C]//Expanded Abstracts CPS/SEG 2004 International Geophysical Conference (Volume Ⅱ).[S. l.]:CPS/SEG, 2004:672-676. |
| [39] | Yooyuanyong S. Mathematical Model of MMR Inver-sion for Geophysical Data[J]. Songklanakarin Journal of Science & Technology, 2007, 29(4): 1417-1426. |
| [40] | Edwards R N, Lee H, Nabighian M N. On the Theo-ry of Magnetometric Resistivity (MMR) Methods[J]. Geophysics, 1978, 43(6): 1176-1203. DOI:10.1190/1.1440887 |
| [41] | Sezginer A, Habashy T M, Wait J R. An Image Me-thod to Compute the Static Magnetic Field Due to Currents Injected into a Homogeneous, Conducting, and Magnetically Polarizable Half-Space[J]. Radio Science, 1988, 23(1): 41-45. DOI:10.1029/RS023i001p00041 |
| [42] | Inayat-Hussain A A. Magnetic Field of a Direct Cu-rrent in a Cylindrical-Shaped Conductor Imbedded in a Resistive Half-Space Beneath a Conductive Surface Layer[J]. J Appl Phys, 1989, 66(10): 4587-4593. DOI:10.1063/1.343812 |
| [43] | Inayat-Hussein A A. Magnetic Fields of Direct Cu-rrents in Horizontally Stratified Conductors[J]. J Appl Phys, 1989, 65(9): 3731-3732. DOI:10.1063/1.342607 |
| [44] | Gómez-Treviño E, Edwards R N. Magnetometric Re-sistivity (MMR) Anomalies of Two Dimensional Structures[J]. Geophysics, 1979, 44(5): 947-958. DOI:10.1190/1.1440987 |
| [45] | Nabighian M N, Oppliger G L, Edwards R N, et al. Cross-Hole Magnetometric Resistivity (MMR)[J]. Geophysics, 1984, 49(8): 1313-1326. DOI:10.1190/1.1441758 |
| [46] | Cheesman S J, Edwards R N. Current Channelling in Square Plates with Applications to Magnetometric Resistivity[J]. Geophys Prospect, 1989, 37: 553-581. DOI:10.1111/gpr.1989.37.issue-5 |
| [47] | Hvoždara M, Kaikkonen P. The Boundary Integral Calculations of the Forward Problem for D C Sounding and MMR Methods for a 3-D Body near a Vertical Contact[J]. Studia Geophysica et Geodaetica, 1994, 38(4): 375-398. DOI:10.1007/BF02296169 |
| [48] | Méndez-Delgado S, Gómez-Treviño E, Pérez-Flores M A. Forward Modelling of Direct Current and Low-Frequency Electromagnetic Fields Using Integral Equations[J]. Geophysical Journal International, 1999, 137(2): 336-352. |
| [49] | Pai D M, Yeoh J P. Downhole Magnetometric Resi-stivity Response of a Half-Plane Conductor[J]. Geophysics, 1987, 52(3): 353-362. DOI:10.1190/1.1442309 |
| [50] | McGillivray P R. Forward Modeling and Inversion of D C Resistivity and MMR Data[D]. Vancouver:The University of British Columbia, 1992. http://circle.ubc.ca/handle/2429/3114 |
| [51] | Yang C H, Tseng H W. Topographic Responses in Magnetometric Resistivity Modeling[J]. Geophysics, 1992, 57(10): 1409-1478. |
| [52] | Boggs D B. The Theory and Application of Sub-Audio Magnetic Data Acquisition and Numerical Modeling[D]. Armidale:University of New England, 1999. http://www.wiley.com/legacy/products/subject/reference/webster_toc.html |
| [53] | Boggs D B, Stanley J M, Cattach M K. Three-Di-mensional Numerical Modeling of Sub-Audio Magnetic Data[J]. Expl Geophys, 1999, 30: 147-156. DOI:10.1071/EG999147 |
| [54] | Lassner L A. Examining the Effects of Mid Ocean Ridge Topography on 3D Marine Magnetometric Resistivity Model Responses[D]. Boston:Massachusetts Institute of Technology, 2004. http://dx.doi.org/10.1575/1912/2071 |
| [55] | Yooyuanyong S, Sripanya W. Mathematical Mode-lling of Magnetometric Resistivity Sounding Earth Structures[J]. Thai Journal of Mathematics, 2005, 3(2): 249-258. |
| [56] | Yooyuanyong S, Sripanya W. Magnetic Field of Di-rect Current in Heterogeneous Ground[J]. Songklanakarin Journal of Science & Technology, 2007, 29(2): 565-573. |
| [57] | Chaladgarn T, Yooyuanyong S. Mathematical Model of Magnetometric Resistivity Sounding for a Conductive Host with a Bulge Overburden[J]. Applied Mathematical Sciences, 2013, 7(7): 335-348. |
| [58] | Butler S L, Zhang Z. Forward Modeling of Geoph-ysical Electromagnetic Methods Using Comsol[J]. Computers & Geosciences, 2015, 87: 1-10. |
| [59] | Howland-Rose A W, Linford G, Pitcher D H, et al. Some Recent Magnetic Induced-Polarization Developments:Part Ⅱ:Survey Results[J]. Geophysics, 1980, 45(1): 55-74. DOI:10.1190/1.1441040 |
| [60] | Szarka L. Geophysical Mapping by Stationary Electric and Magnetic Field Components:A Combination of Potential Gradient Mapping and Magnetometric Resistivity (MMR) Methods[J]. Geophys Prospect, 1987, 35: 424-444. DOI:10.1111/gpr.1987.35.issue-4 |
| [61] | Hishime H, Tsujimoto T M, Humphreys G, et al. MIP Test Survey over the HYC Deposit in Mcarthur River Area, N T[J]. Explor Geophys, 1993, 24: 577-584. DOI:10.1071/EG993577 |
| [62] | Bishop J, Carroll N, Asten M, et al. Finding Spha-lerite at Broken Hill with Drillhole Magnetometric Resistivity[J]. Expl Geophys, 1997, 28: 6-10. DOI:10.1071/EG997006 |
| [63] | Sripanya W. Inverse Problem of Magnetometric Resi-stivity Response from Exponentially Varying Conductive Ground[J]. Adv Studies Theor Phy, 2013, 7(8): 367-374. |
| [64] | Sripanya W. Regularized Inverse Problem of Mag-netometric Resistivity Response over a Layered Earth[J]. Adv Studies Theor Phy, 2013, 7(4): 183-190. |
| [65] | Labrecque D, Sharpe R, Dan C, et al. Combined Electrical and Magnetic Resistivity Tomography:Synthetic Model Study and Inverse Modeling[J]. Journal of Environmental & Engineering Geophysics, 2003, 8(4): 251-262. |
| [66] | Chen J, Oldenburg D W. 3-D Inversion of Magnetic Induced Polarization Data[C]//Aseg Extended Abstracts.[S. l.]:ASEG, 2003(1):245-253. |
| [67] | Li Y, Oldenburg D W. 3D Inversion of Gravity Data[J]. Geophysics, 1998, 63(1): 109-119. DOI:10.1190/1.1444302 |
| [68] | Green W R. Inversion of Gravity Profiles by Use of a Backus-Gilbert Approach[J]. Geophysics, 1975, 40(5): 763-772. DOI:10.1190/1.1440566 |
| [69] | Last B J, Kubik K. Compact Gravity Inversion[J]. Geophysics, 1983, 48(6): 713-721. DOI:10.1190/1.1441501 |
| [70] | Guillen A, Menichetti V. Gravity and Magnetic In-version with Minimization of a Specific Functional[J]. Geophysics, 1984, 49(8): 1354-1360. DOI:10.1190/1.1441761 |
| [71] | Bhattacharyya B K. A Generalized Multibody Model for Inversion of Magnetic Anomalies[J]. Geophysics, 1980, 45(2): 255-270. DOI:10.1190/1.1441081 |
| [72] | Wang X, Hansen R O. Inversion for Magnetic Ano-malies of Arbitrary Three-Dimensional Bodies[J]. Geophysics, 1990, 55(10): 1321-1326. DOI:10.1190/1.1442779 |
| [73] | Zeyen H, Pous J. A New 3-D Inversion Algorithm for Magnetic Total Field Anomalies[J]. Geophysical Journal International, 1991, 104(3): 583-591. |
| [74] | Li Y, Oldenburg D W. 3-D Inversion of Magnetic Data[J]. Geophysics, 1996, 61(2): 394-408. DOI:10.1190/1.1443968 |
| [75] | Li Y, Oldenburg D W. Joint Inversion of Surface and Three-Component Borehole Magnetic Data[J]. Geophysics, 2000, 65(2): 540-552. DOI:10.1190/1.1444749 |
| [76] | Zhdanov M S. Geophysical Inverse Theory and Regu-larization Problems[M]. Amsterdam: Elsevier Academic Press, 2002. |
| [77] | Jakosky J J. Method and Apparatus for Determining Underground Structure:U S, 1906271[P]. 1933-05-02. |
| [78] | Edwards R N. The Magnetometric Resistivity Me-thod and Its Application to the Mapping of a Fault[J]. Can J Earth Sci, 1974, 11: 1136-1156. DOI:10.1139/e74-108 |
| [79] | Edwards R N, Howell E C. A Field Test of the Magnetometric Resistivity (MMR) Method[J]. Geophysics, 1976, 6A(6): 1170-1183. |
| [80] | Seigel H O. The Magnetic Induced Polarization (MIP) Method[J]. Geophysics, 1974, 39(3): 321-339. DOI:10.1190/1.1440431 |
| [81] | Seigel H O, Howland-Rose. Magnetic Induced-Polarization Method[C]//Fink J B, Sternberg B K, Mcalister E O, et al. In Induced Polarization:Applications and Case Histories. Tulsa:SEG, 1990:23-56. |
| [82] | Hashemi A, Meyers J, Rothery E. Sub-Audio Magnetic Surveying for Shallow Occurrences of Conductive Manganese Ore, Woodie Woodie Area, Western Australia[J]. Exploration Geophysics, 2005, 36(2): 170-175. DOI:10.1071/EG05170 |
| [83] | Meyers J, Cantwell N, Nguyen P, et al. Sub-Audio Magnetic Survey Experiments for High-Resolution, Subsurface Mapping of Regolith and Mineralization at the Songvang Gold Mine Near Agnew, Western Australia[J]. Exploration Geophysics, 2005, 36(2): 125-132. DOI:10.1071/EG05125 |
| [84] | Whitford M, Meyers J, Stolz Ned. The SAM EQM-MR Response of the Regolith at East Victory, St Ives Gold Mine, Western Australia[J]. Exploration Geophysics, 2005, 36(2): 133-139. DOI:10.1071/EG05133 |
| [85] | Wallance Y, Card D, Gates K, et al. Identification of Massive Sulphide Targets Using the Galvanic Source EM (GSEM) Signal from a Sub-Audio Magnetic (SAM) Survey at the Far South Project, Western Australia[C]//24th International Geophysical Conference and Exhibition. Perth:[s. n.], 2015:1-4. |
| [86] | Meju M A. Geoelectromagnetic Exploration for Natu-ral Resources:Models, Case Studies and Challenges[J]. Surveys in Geophysics, 2002, 23(2/3): 133-206. DOI:10.1023/A:1015052419222 |
| [87] |
韩凯, 郑智杰, 甘伏平, 等. 利用多源大功率充电法定位复杂岩溶含水通道的方法[J].
吉林大学学报(地球科学版), 2016, 46(5): 1501-1510.
Han Kai, Zheng Zhijie, Gan Fuping, et al. Determination of Complex Karst Water Channel Using Multi-Source High Power Mise-A-La-Masse Method[J]. Journal of Jilin University (Earth Science Edition), 2016, 46(5): 1501-1510. |
| [88] | Street G J. MMR Surveys for the Location of Pa-laeochannels in the Eastern Goldfields, Western Australia[J]. Exploration Geophysics, 1989, 20(2): 123-126. DOI:10.1071/EG989123 |
| [89] | Goldman M, Neubauer F M. Groundwater Exp-loration Using Integrated Geophysical Techniques[J]. Surveysin Geophysics, 1994, 15(3): 331-361. DOI:10.1007/BF00665814 |
| [90] | Kulessa B, Jaekel U, Kemna A, et al. Magne-tometric Resistivity (MMR) Imaging of Subsurface Solute Flow:Inversion Framework and Laboratory Tests[J]. Journal of Environmental & Engineering Geophysics, 2002, 7(3): 111-118. |
| [91] | Labrecque D J, Yang X J. Difference Inversion of ERT Data:A Fast Inversion Method for 3-D in Situ Monitoring[J]. Journal of Environmental & Engineering Geophysics, 2001, 6(2): 316-321. |
| [92] | Kofoed V O. Making Accurate Groundwater Flow Models[J]. Pollution Engineering, 2013, 22: 22-26. |
| [93] | Maxwell M, Eso R, Oldenburg D. Using 2D and 3D Electrical Resistivity and Magnetometric Resistivity Techniques for Investigating Dam and Dike Soil Conditions for Leak Detection:Field Examples and Forward Modeling[C]//Symposium on the Application of Geophysics to Engineering and Environmental Problems 2013.[S. l.]:Environment and Engineering Geophysical Society, 2013:821. |
| [94] | Hayley K, Pidlisecky A, Bentley L R. Simultaneous Time-Lapse Electrical Resistivity Inversion[J]. Journal of Applied Geophysics, 2011, 75(2): 401-411. DOI:10.1016/j.jappgeo.2011.06.035 |
| [95] | Zhu K, Yang J. Time-Lapse Magnetometric Resis-tivity (MMR) Anomalies of Groundwater Contamination Theoretical Results from Computational Hydro-Geophysical Modeling[C]//Goephysical Solutions for Environment and Engineering:Proceedings of the 2nd International Conference on Environmental and Engineering Geophysics(Volume 1).[S. l.]:Environment and Engineering Geophysical Society, 2006:303-307. |
| [96] | Zhu K, Yang J. Time-Dependent Magnetometric Resistivity Anomalies of Groundwater Contaminatin:Synthetic Results from Computational Hydro-Geophysical Modeling[J]. Applied Geophysics, 2008, 5(4): 322-330. DOI:10.1007/s11770-008-0041-3 |
| [97] | Veitch D, Asten M W, Leeuwen E H V. Electrical and Magnetometric Fields in a Layered Earth Containing Buried Electrodes[J]. Geophysics, 1990, 55(12): 1605-1612. DOI:10.1190/1.1442812 |
| [98] | Bishop J, Lewis R, Stolz N. Horses for (Conductive) Courses:DHEM and DHMMR[J]. Exploration Geophysics, 2000, 31(2): 192-199. DOI:10.1071/EG00192 |
| [99] | Meyers J, Cooper M, Bishop J R, et al. Downhole Magnetometric Resistivity Surveying for Refractory Gold Ore at Wiluna Gold Mine[C]//14th ASEG Conf Preview.[S. l.]:ASEG, 2000:79, 84. |
| [100] | Godber K E, Bishop J R. DHMMR:Coming of Age[C]//Exploration in the New Millennium:Proceeding of the Fifth Decennial International Conference on Mineral Exploration. Keystone:AGU-SEG, 2007:1119-1123. |
| [101] | Godber K, Reid J, Duncan A. Looking Left, Right and Centre with DHMMR[C]//ASEG Extended Abstracts. Perth:ASEG, 2007:1-6. |
| [102] | Asten M W. Borehole EM and MMR Methods for Weak Conductors:A Project Review[C]//15th ASEG Extended Abstracts.[S. l.]:ASEG, 2001(1):1-4. |
| [103] | Nabighian M N, Asten M W. Metalliferous Mining Geophysics:State of the Art in the Last Decade of the 20th Century and the Beginning of the New Millennium[J]. Geophysics, 2002, 67(3): 964-978. DOI:10.1190/1.1484538 |
| [104] | VallÉE M A, Smith R S, Keating P. Metalliferous Mining Geophysics:State of the Art After a Decade in the New Millennium[J]. Geophysics, 2011, 76(4): W31-W50. DOI:10.1190/1.3587224 |
| [105] | Edwards R N. A Downhole Magnetometric Resis-tivity Technique for Electrical Sounding Beneath a Conductive Surface Layer[J]. Geophysics, 1988, 53(4): 528-536. DOI:10.1190/1.1442484 |
| [106] | Asten M W. Field Examples of the Downhole MMR Method and Comparison with the TEM Method[C]//Nabighian M N. Electromagnetic Methods in Applied Geophysics.[S. l.]:Soc Expl Geophys, 1991:99-104. |
| [107] | Labrecque D J, Ward S H. Evaluation of Borehole MMR for Fracture Detection[C]//1987 SEG Annual Meeting. New Orleans:[s. n.], 1987(1):923. |
| [108] | Fielitz D, Kemna A, Vereecken H. Sensitivity Di-stributions in 2D Cross-Hole MMR:A Numerical Study[C]//2009 Symposium on the Application of Geophysics to Engineering and Environmental Problems. Fort Worth:SAGEEP, 2009:739-748. |
| [109] | Fielitz D, Kemna A, Zimmermann E, et al. Model Response Curves and Surveying Aspects of 2D Cross-Hole MMR[C]//2009 Symposium on the Application of Geophysics to Engineering and Environmental Problems. Fort Worth:SAGEEP, 2009:801-808. |
| [110] | Bouchedda A, Giroux B. Synthetic Study of CO2 Monitoring Using Time-Lapse Down-Hole Magnetometric Resistivity at Field Reseach Station, Alberta, Canada[C]//2015 SEG New Orleans Annual Meeting. New Orleans:SEG, 2015:5529-5533. |
| [111] | Tada N, Seama N, Goto T N, et al. 1-D Re-sistivity Structures of the Oceanic Crust Around the Hydrothermal Circulation System in the Central Mariana Trough Using Magnetometric Resistivity Method[J]. Earth Planets & Space, 2005, 57(7): 673-677. |
| [112] | Nobes D C, Law L K, Edwards R N. The De-termination of Resistivity and Porosity of the Sediment and Fractured Basalt Layers near the Juan De Fuca Ridge[J]. Geophysical Journal of the Royal Astronomical Society, 1986, 86(2): 289-317. DOI:10.1111/j.1365-246X.1986.tb03830.x |
| [113] | Nobes D C, Law L K, Edwards R N. Results of a Sea-Floor Electromagnetic Survey over a Sedimented Hydrothermal Area on the Juan De Fuca Ridge[J]. Geophysical Journal International, 1992, 110(2): 333-346. DOI:10.1111/gji.1992.110.issue-2 |
| [114] | Evans R L, Webb S C, Marion J, et al. Hydro-thermal Circulation at the Cleft-Vance Overlapping Spreading Center:Results of a Magnetometric Resistivity Survey[J]. Journal of Geophysical Research Solid Earth, 1998, 103(B6): 12321-12338. DOI:10.1029/98JB00599 |
| [115] | Evans R L, Webb S C, Crawford W, et al. Crustal Resistivity Structure at 9°50'N on the East Pacific Rise:Results of an Electromagnetic Survey[J]. Geophysical Research Letters, 2002, 29(6): 6-1-6-4. DOI:10.1029/2001GL014106 |
| [116] | Edwards R N, Wolfgram P A, Judge A S. The ICE-MOSES Experiment:Mapping Permafrost Zones Electrically Beneath the Beaufort Sea[J]. Marine Geophysical Researches, 1988, 9(9): 265-290. |
| [117] | Yang J. Geo-Electrical Responses Associated with Hydrothermal Fluid Circulation in Oceanic Crust:Feasibility of Magnetometric and Electrical Resistivity Methods in Mapping Off-Axis Convection Cells[J]. Exploration Geophysics, 2005, 36(3): 281-286. DOI:10.1071/EG05281 |
| [118] | Baba K. Electrical Structure in Marine Tectonic Settings[J]. Surveys in Geophysics, 2005, 26: 701-731. DOI:10.1007/s10712-005-1831-2 |
| [119] |
傅良魁. 磁激发极化法探矿理论的几个问题[J].
地球物理学报, 1979, 22(2): 156-168.
Fu Liangkui. Several Problems of the Magnetic Induced Polarization (MIP) Method Explorationtheory[J]. Chinese Journal of Geophysics, 1979, 22(2): 156-168. |
| [120] |
励宝恒, 王式铭. 磁激发极化法[J].
物探与化探, 1979, 3(4): 68-73.
Li Baoheng, Wang Shiming. Magnetic Induced Polarization (MIP) Method[J]. Geophysical and Geochemical Exploration, 1979, 3(4): 68-73. |
| [121] |
傅良魁. 磁激发极化法中水平圆柱体的一些研究结果[J].
地球物理学报, 1980, 23(2): 197-206.
Fu Liangkui. Some Results of Research of the Horizontal Cylinder in the Magnetic Induced Polarization Method[J]. Chinese Journal of Geophysics, 1980, 23(2): 197-206. |
| [122] |
崔焕敏, 王刚, 焦宗润. 磁电阻率法与磁激发极化法[J].
放射性地质, 1983, 1(4): 45-54.
Cui Huanmin, Wang Gang, Jiao Zongrun. Magnetometric Resistivity (MMR) Method and Magnetic Induced Polarization (MIP) Method[J]. Radioaction Geology, 1983, 1(4): 45-54. |
| [123] |
张书成. 磁电阻率法的地质效果[J].
地质与勘探, 1987, 23(6): 45-50.
Zhang Shucheng. Geological Results Achieved by Magnetic Resistivity Surveys[J]. Geology and Prospecting, 1987, 23(6): 45-50. |
| [124] |
杨建文. 起伏地形点电源地下传导电流磁场表达式:磁电阻率法地形改正[J].
桂林冶金地质学院学报, 1991, 11(1): 77-87.
Yang Jianwen. The Expressions for Magnetic Fields Associated with the Non-Inductive Current of Point Source in Arbitrarily Undulatory Topography-Topographic Correction of the Magnetometric Resistivity Method[J]. Journal of Guilin College of Geology, 1991, 11(1): 77-87. |
| [125] |
杨建文, 任怀宗. 二度地形的磁电阻率异常计算方法的研究[J].
中南矿冶学院学报, 1991, 22(3): 223-231.
Yang Jianwen, Ren Huaizong. Calculation Method of Magnetometric Resistivity (MMR) Anomalies for 2-D Topographies[J]. Journal of Central South Institute Mining and Metallurgy, 1991, 22(3): 223-231. |
| [126] |
杨建文, 任怀宗, 雷林源. 起伏地形条件下磁电阻率法的资料处理方法[J].
中南矿冶学院学报, 1991, 22(1): 1-8.
Yang Jianwen, Ren Huaizong, Lei Linyuan. Topographic Correction of Magnetometric Resistivity Method[J]. Journal of Central South Institute Mining and Metallurgy, 1991, 22(1): 1-8. |
| [127] |
翁爱华, 刘云鹤, 高丽娟, 等. 天然气水合物的磁电阻率响应特征[J].
石油地球物理勘探, 2009, 44(增刊 1): 158-161.
Weng Aihua, Liu Yunhe, Gao Lijuan, et al. Magnetoelectric Resistivity Reponse Characteristics for Natural Gas Hydrate[J]. Oil Geophysical Prospecting, 2009, 44(Sup. 1): 158-161. |
| [128] |
林品荣, 郭鹏, 石福升, 等. 大深度多功能电磁探测技术研究[J].
地球学报, 2010, 31(2): 149-154.
Lin Pinrong, Guo Peng, Shi Fusheng, et al. A Study of the Techniques for Large-Depth and Multi-Functional Electromagnetic Survey[J]. Acta Geoscientica Sinica, 2010, 31(2): 149-154. |
| [129] |
林品荣, 郑采君, 石福升, 等. 电磁法综合探测系统研究[J].
地质学报, 2006, 80(10): 1539-1548.
Lin Pinrong, Zheng Caijun, Shi Fusheng, et al. The Research of Integrated Electromagnetic Method System[J]. Acta Geologica Sinica, 2006, 80(10): 1539-1548. DOI:10.3321/j.issn:0001-5717.2006.10.007 |
| [130] | Li J, Lin P, Shi F, et al. Study on Magnetic Induced Polarization Technology and Instruments[J]. Applied Mechanics and Materials, 2013, 336-338: 100-105. DOI:10.4028/www.scientific.net/AMM.336-338 |
| [131] |
王猛, 张汉泉, 伍忠良, 等. 勘查天然气水合物资源的海洋可控源电磁发射系统[J].
地球物理学报, 2013, 56(11): 3708-3717.
Wang Meng, Zhang Hanquan, Wu Zhongliang, et al. Marine Controlled Source Electromagnetic Launch System for Natural Gas Hydrate Resource Exploration[J]. Chinese Journal of Geophysics, 2013, 56(11): 3708-3717. DOI:10.6038/cjg20131112 |