2. 吉林大学环境与资源学院, 长春 130021
2. College of Environment and Resources, Jilin University, Changchun 130021, China
0 引言
地下水人工回灌作为进行季节性和多年性地下水资源调节、防止地下含水层枯竭的行之有效的方法,已得到广泛的应用[1-3]。然而,地下水人工回灌中堵塞的产生导致回灌水量不能按照预定目标对地下水进行有效的补给。国内外学者根据堵塞的成因性质将其划分为物理堵塞、化学堵塞及生物堵塞3种类型[4-7]。悬浮物堵塞是注水井与地表回灌系统最常见的物理堵塞之一[8-10],也是造成多数回灌工程失效甚至报废的最主要堵塞形式[11-13]。
目前,对于地下水回灌悬浮物堵塞机理的研究,国内外学者在悬浮物粒径和浓度等问题上已经取得了大量的成果:陈思宁等[14]通过室内砂柱模拟试验发现悬浮物流入砂样浅表层孔隙后,在砂样顶部沉积形成淤泥层,认为淤泥层是渗透速率下降的关键因素;路莹等[15]通过将悬浊水连续注入均质的石英砂柱的室内模拟实验,来刻画多孔介质中悬浮物堵塞的现象及发生的过程,结果表明随入渗深度的增加堵塞程度明显降低;Katarzyna[16]通过室内模拟实验来描述堵塞的微观结构以及介质粒径大小的分布对堵塞速率和程度的影响;王子佳等[17]研究发现悬浮物粒径与入渗介质孔径之间的关系是决定堵塞类型的重要指标;单蓓蓓等[18]采用土柱渗流实验对回灌液悬浮物浓度和水动力条件对堵塞的影响进行了研究,结果表明进水和出水的水头差越大、水力坡度越大,悬浮物颗粒在流体的剪切力作用下运移深度越大,造成含水层堵塞的范围就越大;Zamani等[19]发现悬浮颗粒淤积会改变含水介质孔隙特征,使得其孔隙度和局部压力发生变化,导致介质渗透性下降。
在实际的人工回灌过程中,伴随着水位的升高,地下水动力学条件(注水水位与地下水位之间的差值)的改变会影响回灌效率和物理堵塞的发生及发展过程。本文通过室内实验研究由地下水抬升对悬浮颗粒在多孔介质中迁移-沉积造成的含水介质堵塞规律。首先通过土柱渗流模拟实验,采用分层测定渗透系数的方法来研究堵塞造成的含水介质非均质性,然后,研究地下水位抬升对回灌水中悬浮物沉积在含水介质中的级配的影响;以期对开展实际回灌工程(特别是地表入渗回灌)系统设计与运行方案的制定提供一定的理论指导与参考。
1 实验材料与装置 1.1 实验材料模拟人工回灌含水层砂样是粒径为0.25~0.50 mm的石英砂,实验前用去离子水冲洗石英砂以去除其中的细小粉末。以金刚砂模拟野外回灌雨洪水中的悬浮物,配置质量浓度为100.00 mg/L,其颗粒组成如表 1所示。实验用水为经0.10 μm滤膜过滤过的自来水。
| 粒径/μm | 体积分数/% |
| <15 | 33.61 |
| 15~30 | 33.94 |
| 30~45 | 21.85 |
| 45~100 | 10.60 |
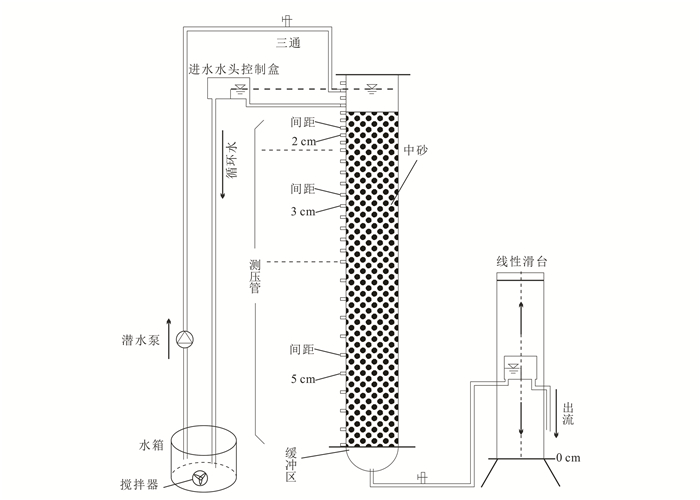
实验装置主要由供水装置、实验砂柱和定水头装置构成,实验设备如图 1所示。供水装置由供水泵通过三通对3组砂柱同时进行供水;砂柱由5 mm厚的有机玻璃制成,高105 cm,内径为10 cm。柱体由两部分组成:上部为100 cm的渗流区,侧面共分布有30个测压孔,由上至下,1—10号测压孔间距为2 cm,10—20号为3 cm,20—30号为5 cm;下部为5 cm的水流缓冲区;进、出水的定水头装置是采用溢流原理控制供水和排水水位,可通过线性滑台上、下自由调节高度[20]。
|
| 图 1 实验装置图 Figure 1 Experimental apparatus figure |
|
|
此实验共分为以下3个阶段:1)测3个砂柱密度及初始孔隙度,确保其填充状态相同;2)实验前,先用清水对3组砂柱同时供水,以使水头及出水量分别达到稳定且一致,然后金刚砂悬浊液供水;3)3组砂柱出水水头初始位置均与在砂柱出水口处持平,控制定水头装置改变砂柱出水水位。柱1出水水头固定不变;柱2出水水位抬升速率为2 cm/h,抬升20 h;柱3出水水位抬升速率4 cm/h,抬升10 h;柱2、柱3抬升高度共计40 cm,实验方案见表 2。
| 砂柱编号 | 出水水位抬升速度/(cm/h) | 抬升时间/h | 砂柱密度/(g/cm3) | 砂柱填充高度/cm | 进水水头高度/cm | 砂柱初始孔隙度 |
| 1# | 0 | 0 | 1.71 | 92.00 | 100.10 | 0.34 |
| 2# | 2 | 20 | 1.75 | 92.00 | 99.60 | 0.33 |
| 3# | 4 | 10 | 1.74 | 92.00 | 100.50 | 0.33 |
实验过程中,对3组砂柱各层水位、水量及堵塞层等进行观察记录。实验结束后拆柱,每2 cm取样一次,通过对堵塞层中的悬浮物筛选计算其所占比例,然后对筛出的悬浮颗粒进行颗粒级配和分析。
3 实验结果与讨论 3.1 水位抬升对堵塞位置与堵塞程度的影响悬浮物堵塞是指由悬浮物质沉积在介质孔隙中所引起的渗透性降低现象,因此常通过渗透系数的变化来判断堵塞现象发生与否。一般来说,在饱和渗流过程中,通常采用K/K0值作为判定堵塞发生的标准(其中K与K0分别为某一时刻与初始时刻的渗透系数):K/K0≥1说明没有发生堵塞现象;K/K0<1则说明可能发生了堵塞[21]。而当表面或浅层堵塞发展到一定程度,导致入渗水量小于排出水量时,多孔介质会出现非饱和渗流过程,此时的渗透系数还与含水率的变化有关;对于堵塞的识别需采用测量渗流路径上沉积的悬浮物质量分数的方法。
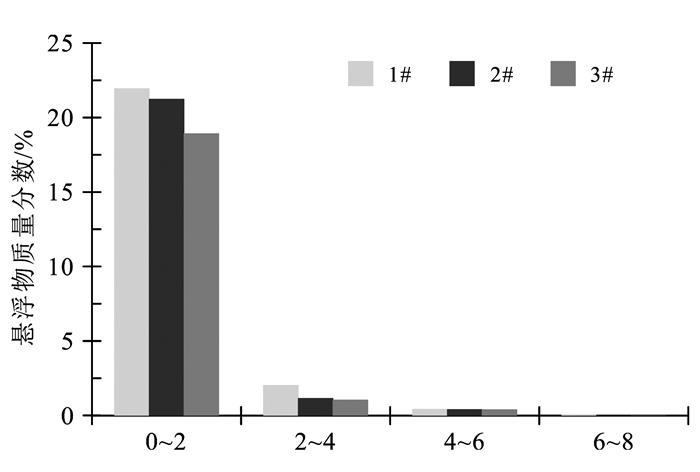
3.1.1 水位抬升对堵塞位置的影响实验结束后,首先分别对3组砂柱进行取样;再进行砂柱表层内悬浮物取样的测定(此时位于8 cm以下的层位没有检出悬浮物);然后绘制3组砂柱中堵塞层悬浮物质量分数图(图 2)。
|
| 图 2 堵塞层悬浮物质量分数 Figure 2 Clogging layer of suspended solids in the percentage of the total quality of every layer |
|
|
从图 2可看出,地下水位抬升对堵塞发生的位置影响不大,不同水位抬升速率情况下,堵塞均发生在表层0~2、2~4和4~6 cm处,而0~2 cm是堵塞的主要位置。
3.1.2 水位抬升对堵塞程度的影响本实验水流方向垂直于砂柱各层,因此渗透介质整体渗透系数与各层渗透系数的关系为
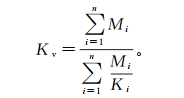 (1)
(1) 式中:Kv为砂柱整体等效渗透系数,m/d;Ki为砂柱第i层渗透系数,m/d;Mi为砂柱第i层厚度,cm;n为砂柱分层数。
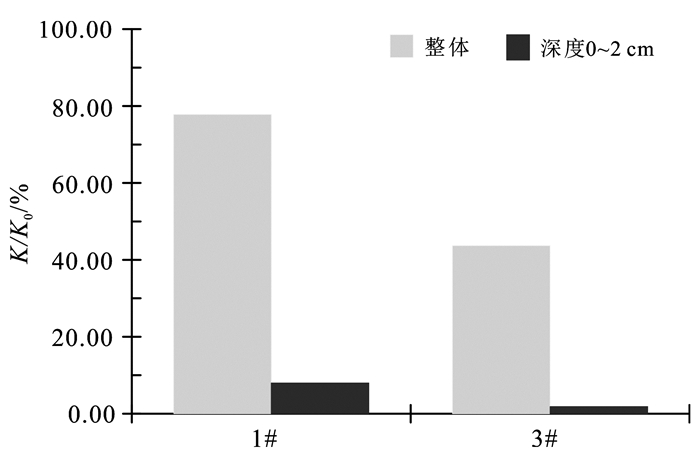
由式(1)可知,砂柱任何一层渗透系数的变化都会引起砂柱整体渗透系数的改变,但整体渗透系数的变化程度与各层渗透系数的变化程度并不一定相同。因这种判别方法仅可用于饱和渗流过程,故选取3组砂柱出现非饱和渗流前一时刻的K/K0进行比较。1#、3#出现非饱和前一时刻分别为10 h、44 h(2#在0~2 cm处的观测孔损坏,因此只比较1#和3#的区别)。绘制2组砂柱堵塞层0~2 cm与介质整体渗透系数K/K0的变化,如图 3所示。
|
| 图 3 不同抬升速率与渗透系数变化的关系 Figure 3 Relationship of water different level rising and clogging degree |
|
|
由图 3可知:1#、3#的整体渗透系数分别减少了22.22%、56.29%;1#、3#在堵塞层0~2 cm渗透系数分别减少了92.02%、98.14%。这说明介质表层0~2 cm是发生堵塞的主要层位,堵塞层位是砂柱整体的渗透系数降低的主要原因;同时,水位抬升引起渗透系数减小程度更大。
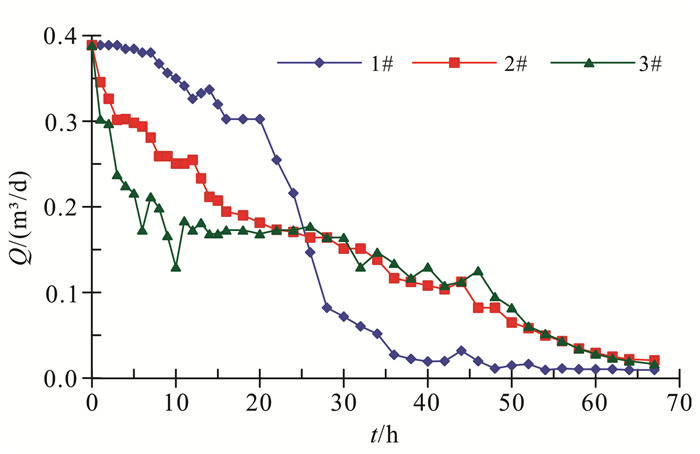
3.2 水位抬升对入渗量的影响绘制3组实验中入渗量随时间的变化曲线,如图 4所示。
|
| 图 4 入渗量Q随时间t的变化 Figure 4 Infiltration recharge (Q) change with time (t) |
|
|
在整个实验过程中,3组砂柱的入渗量均有降低,说明随着实验的进行,悬浮物颗粒进入到入渗介质,引起入渗介质堵塞,使得入渗量逐渐降低。在0~26 h,1#、2#、3#的入渗量依次减少,其中2#、3#因水位抬升引起入渗补给进入介质中的水量降低得更快,且3井水位抬升幅度更大,引起入渗量降低幅度也更大;在26~67 h,2#、3#的入渗量近似一致,均大于1#,这是因为随着回灌时间的延续,悬浮物堵塞进一步加剧,入渗量进一步减少,并且在堵塞层下方砂层出现负压现象,出现不饱和状态,但由于2#、3#出水水位较高,使得其毛细上升力较1#的大,进一步加强了堵塞层与非堵塞层之间的水力联系,从而其入渗量较1#的大。
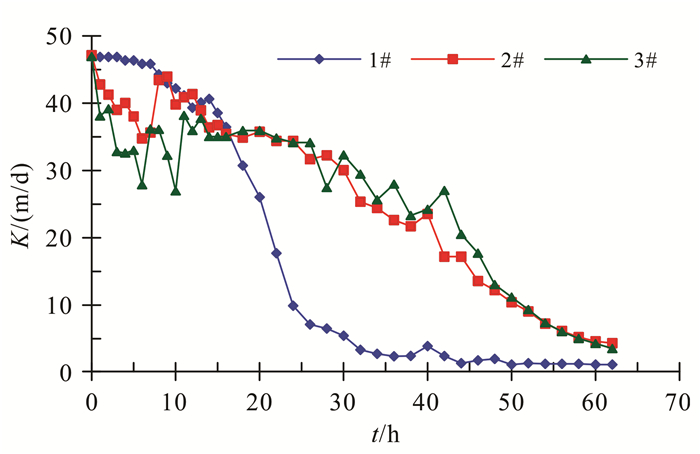
3.3 介质渗透系数随时间的变化规律 3.3.1 砂柱整体渗透系数变化特征向中粒石英砂介质中注入悬浊水后,发现3组砂柱整体渗透系数随时间的变化大体可分为3个阶段,如图 5所示。
|
| 图 5 砂柱整体渗透系数随时间的变化 Figure 5 Whole sand column permeability coefficient changes with 16:17:11 |
|
|
回灌初期:在16 h之前,3组砂柱整体渗透系数均在下降;说明随着悬浮物颗粒进入多孔介质,入渗介质孔隙变小,渗透系数逐渐降低,但受水位抬升引起的入渗量及水力梯度减少的综合影响,1#、3#、2#的入渗量依次减少,2#、3#渗透系数比1#渗透系数的小。
回灌中期:在16~35 h期间,3组砂柱渗透系数整体均有较大幅度的下降,2#、3#渗透系数变化趋势基本一致,且二者的渗透系数均大于1#。1#渗透系数急剧减小的时间段为16~30 h,而其流量急剧减小的时间段为20~40 h,滞后于渗透系数的变化;经观察,在16 h时1#的堵塞层4 cm以下观察孔中均出现负压,出现非饱和状态;且1#出水水头过低,其毛细上升带不能够很好地连接到堵塞层,水流不能透过堵塞层发生稳定的渗流,随着悬浮物在砂柱表层的淤积增大到一定程度,透过堵塞层的水量大大减少,导致其渗透系数在16~30 h急剧减小。因受水位抬升的影响,在16~20 h,2#、3#渗透系数波动不稳定;20 h后,2#、3#的出水水头高度相同,20~58 h的渗透系数及入渗量均在急剧降低,且二者分别趋于重合,2#、3#在堵塞层4~6 cm的观测孔中看到气泡分别出现在第50 h和第48 h,原理与1#相同。
回灌后期:1#在30~62 h入渗量与渗透系数很小且基本稳定,这是由于1#悬浮物堵塞发展程度已经十分缓慢,透过堵塞层的水量很少并趋于不变,堵塞层以下的砂层进行近乎疏干排水的过程。在58~62 h,2#、3#渗透系数缓慢减小,且渗透系数趋于不变,说明此时二者将进入到疏干排水的阶段。
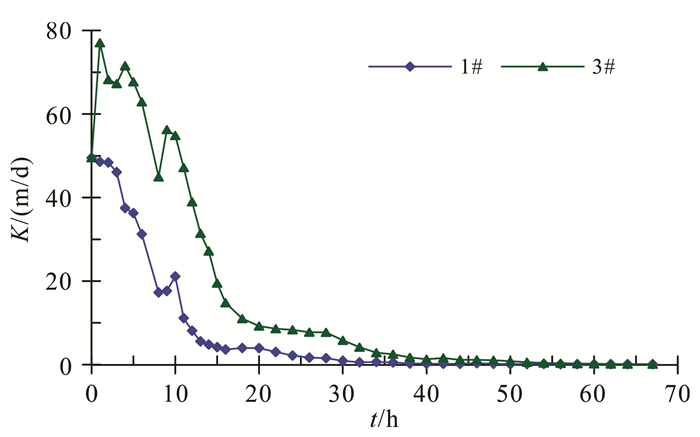
3.3.2 堵塞层渗透系数变化特征比较1#、3#在0~2 cm处的渗透系数(图 6)可知:在35 h之前,3#在堵塞层0~2 cm渗透系数整体大于1#,35 h之后二者在堵塞层0~2 cm渗透系数近似重合,但在整个时间段内二者的变化趋势是一致的。这说明:在35 h前,3#(水位抬升期间10 h)入渗量因水位抬升而降低,同时扰乱并降低了悬浮物进入介质孔隙,减缓了堵塞的发生,因此,其在堵塞层0~2 cm渗透系数较1#大;3#在水位固定不变后,随着介质孔隙中悬浮物堵塞的发展,35 h后1#、3#透过堵塞层0~2 cm入渗到下部砂层的水量非常少,故二者的渗透系数近似相同。
|
| 图 6 砂柱0~2 cm深度处渗透系数随时间的变化 Figure 6 Sand column 0-2 cm depth of permeability coefficient change with 16:17:26 |
|
|
随着回灌的进行,悬浮物颗粒进入介质孔隙,并向下迁移,逐渐淤积在表层。悬浊水透过堵塞层补给到非堵塞层的水量减少,堵塞层下方逐渐由饱和状态过渡到非饱和状态,非饱和状态出现的宏观标志为观测到非堵塞层下方测压管出现负压,微观标志为某一深度的测压水头低于该点的位置水头。
1) 非饱和状态
根据达西定律,渗透系数可以表达为
 (2)
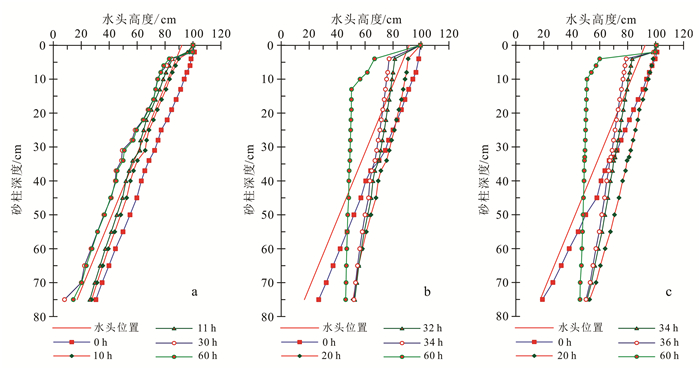
(2) 式中:v为渗透速度,m/d;I为水力梯度。式(2)只适用于饱和状态下的稳定流,故可通过砂柱各层深度处测压水头与其位置水头的大小关系,判断其是否进入非饱和状态,进而分析介质垂向渗流变化特征。因此,绘制1#、2#、3#不同时刻的各深度的测压水头的变化曲线,如图 7所示。
|
| a.1#;b.2#;c.3#。 图 7 测压水头垂向变异特征 Figure 7 Vertical variation characteristics of pressure head |
|
|
3组砂柱堵塞层均为0~10 cm,均以10 cm深度处出现测压水头小于其水头位置的时刻标志砂柱进入非饱和渗流状态。由图 7可看出,1#、2#、3#在堵塞层0~10 cm出现测压水头低于水头位置的时刻分别为第11、32、34 h,宏观上3组砂柱测压管出现负压分别在第16、50、48 h时刻;这说明堵塞引起堵塞层下方介质出现非饱和现象从产生到宏观表现有滞后的效应,水位抬升引起砂柱表层堵塞速率变缓(详见3.4.2),非堵塞层入渗介质出现非饱和状态的出现滞后。
2)饱和状态
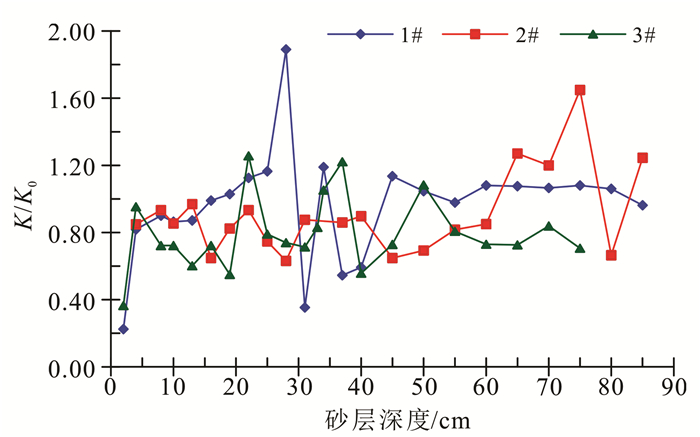
根据上述结论,分别选取1#、2#、3#在第10、20、20 h时刻的饱和状态,对其垂向上的渗透系数与初始时刻的渗透系数的比值K/K0进行比较,如图 8所示。
|
| 图 8 渗透系数变化的垂向变异特征 Figure 8 Vertical variation characteristics of permeability coefficient changing |
|
|
在0~8 cm处,3组砂柱渗透系数较小,且差别不大,说明堵塞层渗透系数基本不受水位抬升影响;8~80 cm处,1#、2#、3#的K/K0值分别在0.35~1.89、0.63~1.65、0.55~1.26之间波动,相差不大,说明水位抬升引起非堵塞层渗透系数偏离初始值的波动幅度较水位固定的波动幅度变化不大。
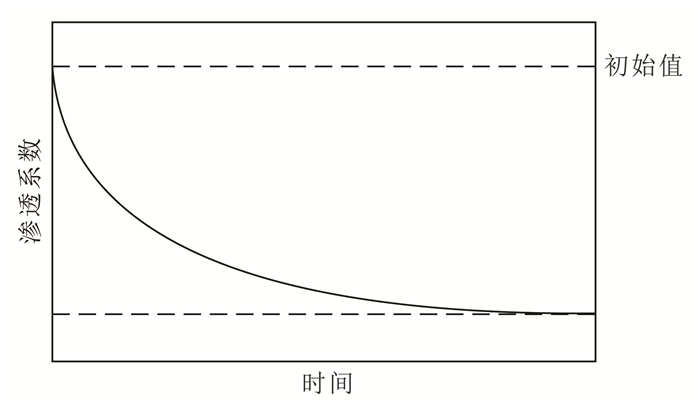
3.4 水位抬升对堵塞速率的影响 3.4.1 堵塞速率的表征为了描述细颗粒悬浮物在含水介质孔隙产生的堵塞速率,引入Bianchi等[22]在1978年提出的可以描述多种堵塞问题的概括性方程,建立了堵塞过程中渗透系数随时间变化的数学模型,如图 9所示,其过程可以表示为
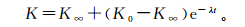 (3)
(3)
|
| 图 9 渗透系数随时间变化典型曲线 Figure 9 Typical curve of coefficient of permeability changing with 16:18:05 |
|
|
式中:K∞为终点时刻渗透系数,m/d;λ为经验参数,控制堵塞速率;t为时间,d。
此模型代表堵塞形成过程中渗透系数的衰减情况。当模型参数确定后,可根据初始渗透系数、终点渗透系数推求任意时刻的渗透系数值。在实际情况下,可用离散点近似表示连续的堵塞方程。λ即是表征堵塞速率的物理量,λ越大堵塞速率越大。
刘国庆等[23]参考Bianchi等[22]的可以描述多种堵塞问题的概括性方程,以何满潮等[24-25]建立的渗透系数衰减模型为基础,结合Theis公式,获得了考虑渗透系数衰减以及暂时性堵塞率条件下回灌与回扬物理过程中含水层压强的解析表达式,准确地刻画了回灌与回扬物理过程。因此,此模型方程还可表达为
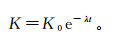 (4)
(4) 式(4)可描述细颗粒悬浮物在含水介质孔隙产生的堵塞速率,主要表征含水层从未堵塞到堵塞末的时刻。本文实验中出水水位抬升的砂柱在抬升期间,渗透系数出现波动,不是持续降低。由图 10可看出,本文中出水水位抬升的砂柱(3#)堵塞层堵塞速率计算分为2个阶段,水位抬升期和水位稳定后至终点时刻。

|
| 图 10 1#和3#在0~2 cm深度处渗透系数曲线拟合图 Figure 10 Curve fitting of permeability coefficient of column 1 and column 3 in the 0-2 cm depth |
|
|
根据式(4)分别计算堵塞层0~2 cm处,1#在0~62 h时间段和3#在0~10 h、10~62 h时间段的λ,结果见表 3。
| 分组 | λ | ||
| 0~62 h | 0~10 h | 10~62 h | |
| 1# | 0.132 | ||
| 3# | 0.017 | 0.109 | |
在整个实验过程中,1#堵塞速率比3#的大,1#出水水位固定的砂柱堵塞速率曲线可以和实测点拟合得很好(图 10),说明水位抬升可扰动并减缓悬浮物进入介质孔隙,进而延缓堵塞的发展,堵塞速率减小。3#水位抬升使得堵塞速率变化很大(图 10):在抬升期间(0~10 h)堵塞速率很小,λ为0.017;在10~60 h,水位稳定后堵塞速率有所升高,λ为0.109。
3.5 沉积在介质中悬浮物级配特征通过计算得出100 mg/L的悬浊液回灌入渗3组中砂介质时淤积的悬浮物在堵塞层0~2 cm的粒径级配,3组粒径级配与原始砂样接近一致,见表 4。表 4说明在这种抬升幅度和周期下,本次实验中悬浮物的级配变化不大。
| 分组 | φB/% | |||
| <15 | 15~30 | 30~45 | 45~60 | |
| 原始配比 | 33.61 | 33.94 | 21.85 | 10.60 |
| 1# | 32.30 | 34.09 | 22.45 | 11.16 |
| 2# | 33.82 | 33.26 | 21.93 | 10.89 |
| 3# | 27.67 | 39.48 | 21.95 | 10.10 |
1) 3组砂柱堵塞均发生在表层6 cm内,0~2 cm是主要堵塞层,水位抬升对堵塞的位置影响不大。
2) 在26 h前地下水位抬升引起的入渗量比地下水位固定的入渗量小,在26 h后二者相反。
3) 水位抬升使介质表层堵塞发展速度减慢,非堵塞层渗流状态出现非饱和时刻滞后。
4) 水位抬升会使堵塞速率变小,从而延缓堵塞的发展。
| [1] |
韩再生. 为可持续利用而管理含水层补给:第四届国际地下水人工补给会议综述[J].
水文地质工程地质, 2002, 29(6): 72-73.
Han Zaisheng. Management of Aquifer Recharge for Sustainahility:Review on 4th International Groundwater Artificial Recharge[J]. Hydrogeology and Engineering Geology, 2002, 29(6): 72-73. |
| [2] |
王小刚, 陈松, 王秀芹, 等. 德州市地面沉降成因及防治对策浅析[J].
地质灾害与环境保护, 2006, 17(3): 62-66.
Wang Xiaogang, Chen Song, Wang Xiuqin, et al. A Discussion on the Causes of the Ground Subsidence and Its Countermeasures in Dezhou City[J]. Journal of Geological Hazards and Environment Preservation, 2006, 17(3): 62-66. |
| [3] |
冶雪艳, 耿冬青, 杜新强, 等. 工程降水中人工回灌综合技术[J].
世界地质, 2011, 30(1): 90-97.
Ye Xueyan, Geng Dongqing, Du Xinqiang, et al. Integrated Technique of Artificial Recharge in Engineering Dewatering[J]. Global Geology, 2011, 30(1): 90-97. |
| [4] |
上海市水文地质大队.
地下水人工回灌[M]. 北京: 地质出版社, 1977: 173-177.
The Team of Hydrogeology in Shanghai City. Artificial Recharge of Groundwater[M]. Beijing: Geological Press, 1977: 173-177. |
| [5] |
杜新强, 冶雪燕, 路莹, 等. 地下水人工回灌堵塞问题研究进展[J].
地球科学进展, 2009, 24(9): 973-980.
Du Xinqiang, Ye Xueyan, Lu Ying, et al. Advances in Clogging Research of Artificial Recharge[J]. Advances in Earth Sience, 2009, 24(9): 973-980. |
| [6] | Vigneswaran S, Suazo R B. A Detailed Investigation of Physical and Biological Clogging During Artificial Recharge[J]. Water Air and Soil Pollution, 1987, 35(1/2): 119-140. |
| [7] | De Vries J. Soil Filtration of Wastewater Effluent and the Mechanism of Pore Clogging[J]. Water Pollute Control, 1972, 44(2): 565-573. |
| [8] |
黄修东, 束龙仓, 刘佩贵, 等. 注水井回灌过程中堵塞问题的试验研究[J].
水利学报, 2009, 40(4): 430-434.
Huang Xiudong, Shu Longcang, Liu Peigui, et al. Experimental Study on Clogging of Recharge Well[J]. Journal of Hydraulic Engineering, 2009, 40(4): 430-434. |
| [9] | Siriwardene N, Deletic A, Fletcher T D. Clogging of Stormwater Gravel Infiltrtion Systems and Filters:Insights from a Laboratory Study[J]. Water Research, 2007, 41(7): 1433-1440. DOI:10.1016/j.watres.2006.12.040 |
| [10] | Stein P C. A Study of the Theory of Rapid Sand Filtration of Water Through Sand[D]. Cambridge:Massachusetts Institute of Technology, 1940. |
| [11] |
孙颖, 苗礼文. 北京市深井人工回灌现状调查与前景分析[J].
水文地质工程地质, 2011, 28(1): 21-23.
Sun Ying, Miao Liwen. Current Situation Investigation and Prospect Analysis of Artificaial Recharge of Groundwater in Beijing City[J]. Hydrogeology and Engineering Geology, 2011, 28(1): 21-23. |
| [12] |
缪晓图. 苏州市深层水回灌堵塞原因及对策[J].
江苏地矿信息, 1999, 24(3): 86-87.
Miao Xiaotu. Clogging Reasons and Countermeasures of Deep Water Recharge in Suzhou City[J]. Jiangsu Geology and Mineral Resources Information, 1999, 24(3): 86-87. |
| [13] | Lindsey G, Roberts I, Page W. Inspection and Main-tenance of Infiltration Facilities[J]. Journal of Soil and Water Conservation, 1992, 47(6): 481-486. |
| [14] |
陈思宁, 石军, 徐洁, 等. 室内人工回灌试验中几个问题的探讨[J].
水电能源科学, 2010, 28(10): 41-43.
Chen Sining, Shi Jun, Xu Jie, et al. Discussion on Several Problems in Artificial Recharge Experiment[J]. International Journal Hydroelectric Energy, 2010, 28(10): 41-43. DOI:10.3969/j.issn.1000-7709.2010.10.014 |
| [15] |
路莹, 杜新强, 迟宝明, 等. 地下水人工回灌过程中多孔介质悬浮物堵塞实验[J].
吉林大学学报(地球科学版), 2011, 41(2): 448-454.
Lu Ying, Du Xinqiang, Chi Baoming, et al. The Porous Media Clogging Due to Suspended Solid During the Artificial Recharge of Groundwater[J]. Journal of Jilin University (Earth Science Edition), 2011, 41(2): 448-454. |
| [16] | Katarzyna S. Clogging Microstructures in the Vadose Zone-Laboratory and Field Studies[J]. Hydrogeology Journal, 2006, 14(6): 1005-1017. DOI:10.1007/s10040-006-0027-2 |
| [17] |
王子佳, 杜新强, 冶雪艳, 等. 城市雨洪水地下回灌过程中悬浮物堵塞规律[J].
吉林大学学报(地球科学版), 2012, 42(2): 492-498.
Wang Zijia, Du Xinqiang, Ye Xueyan, et al. Suspended Solid Surface Clogging During Urban Stormwater Groundwater Recharge[J]. Journal of Jilin University (Earth Science Edition), 2012, 42(2): 492-498. |
| [18] |
单蓓蓓, 郑西来, 乔振基, 等. 人工回灌过程中含水介质物理堵塞的试验研究[J].
中国海洋大学学报, 2013, 43(10): 97-101.
Shan Beibei, Zheng Xilai, Qiao Zhenji, et al. Experimental Study of Aquifer Physical Clogging During Artificial Recharge Process[J]. Periodical of Ocean University of China (Earth Science Edition), 2013, 43(10): 97-101. |
| [19] | Zamani A, Maini B. Flow of Dispersed Particles Through Porous Media-Deep Bed Filtration[J]. Journal of Petroleum Science and Engineering, 2009, 69(1/2): 71-88. |
| [20] |
刘凯, 文章, 梁杏, 等. 一维低渗透介质非达西渗流实验[J].
水动力学研究与进展:A辑, 2013, 28(1): 81-87.
Liu Kai, Wen Zhang, Liang Xing, et al. One-Dimensional Column Test for Non-Darcy Flow in Low Permeability Media[J]. Journal of Hydrodynamics:Serious A, 2013, 28(1): 81-87. |
| [21] |
石旭飞. 地下水人工回灌过程中的悬浮物堵塞规律研究[D]. 长春: 吉林大学, 2008.
Shi Xufei.Study on Suspended Solid Clogging Mechanism During the Artificial Recharge of Groundwater[D]. Changchun: Jilin University, 2008. |
| [22] | Bianchi W C, Nightingale H I, Mc Cormick R L. A Case History to Evaluate the Performance of Water-Spreading Projects[J]. AWWA, 1978, 70(3): 176-180. |
| [23] |
刘国庆, 吴时强, 范子武, 等. 回灌与回扬物理过程的解析推导及灌压变化规律[J].
吉林大学学报(地球科学版), 2016, 46(6): 1799-1807.
Liu Guoqing, Wu Shiqiang, Fan Ziwu, et al. Analytical Derivation on Recharge and Periodic Backwashing Process and the Variation of Recharge Pressure[J]. Journal of Jilin University (Earth Science Edition), 2016, 46(6): 1799-1807. |
| [24] |
何满潮, 刘斌, 姚磊华, 等. 地热单井回灌渗流场理论研究[J].
太阳能学报, 2003, 24(2): 197-200.
He Manchao, Liu Bin, Yao Leihua, et al. Study on the Theory of Seepage Field for Geothermal Single Well Reinjectong[J]. Acta Energiae Solaris Sinica, 2003, 24(2): 197-200. |
| [25] |
何满潮, 刘斌, 姚磊华, 等. 地下热水回灌过程中渗透系数研究[J].
吉林大学学报(地球科学版), 2002, 32(4): 374-377.
He Manchao, Liu Bin, Yao Leihua, et al. Conductivity During Geothermal Reinjection[J]. Journal of Jilin University (Earth Science Edition), 2002, 32(4): 374-377. |



