0 引言
自然界中地质条件变化多样,几乎不存在完全均质的地质单元。在地下水数值模型构建过程中,往往需要将空间离散为若干个相对均质的小的地质单元体进行差分计算。但由于实际工作中能够获得野外观测资料有限,很难准确确定每个地质单元体的水文地质参数,通常将每个含水层分别简化为若干个较大的相对均质的参数分区。在每个参数分区内,各个地质单元体水文地质参数均匀分布,分区内的参数值可以大致地模拟含水层的整体情况;但在含水层的局部区域,由于非均质性的影响,模拟结果很难真实刻画实际的地下水运动状态。本文以地下水数值模拟中运用最为普遍的MODFLOW软件为基础,考虑到水文地质参数变异性的影响,将水文地质参数进行随机模拟,运用到非均质性含水层的数值模拟中。
含水介质空间结构的复杂性和非均质性直接反映在水文地质参数空间变异特征上,因此对含水介质非均质性的刻画也就是对水文地质参数空间变异性的确定[1]。20世纪70年代以来,随着随机理论研究方法的提出,水文地质参数空间变异性迅速成为水文地质工作者的研究热点内容[2-6]。非均质性是一个相对的概念,主要是沉积环境、成岩作用和构造作用在地质历史时期共同作用的结果,在地下水系统中,含水介质的渗透系数、孔隙度、给水度等参数的空间变异以不同的尺度存在[1]。其中渗透系数是含水介质非均质特征的重要表征参数,与其他水文地质参数相比,其空间变异性较大,在某些地区,渗透系数的最大值与最小值相差可达13个数量级[7];因此,含水介质非均质性的研究多以渗透系数的空间变异特征为对象。这种变异性并不是纯随机的,而是具有不确定变异与确定性变异的特点,即水文地质参数的空间变异具备随机性与结构性的双重性质。
20世纪60年代初期,法国著名地质学家Matheron将南非矿山地质工程师Krige的研究成果理论化、系统化,提出了区域化变量理论,创立了地质统计学(Geostatistics)[8],其核心是Kriging方法,已被广泛应用于多个领域。其几乎是20世纪中后期以来最广泛应用的地理空间插值方法[9]。施小清等[10]采用普通Kriging法进行空间插值以推估上海第Ⅲ承压含水层渗透系数空间分布;同时,此方法已成熟运用于地理信息系统软件Arcgis中以实现高程的区域性插值过程[11]。20世纪90年代,随着地质统计学的发展,基于Monto-Carlo方法设计的条件模拟方法克服了Kriging估值的平滑效应问题,同时对所预测的空间数据可能的取值结果及其概率进行度量,在空间估值的不确定性度量方面开辟了一个新的途径[12]。美国斯坦福大学的Deutsch等[13]以地质统计学为基础,开发了Gslib程序库,它包含了大多数的地质统计学计算方法,在油藏地质建模[14-15]、土壤学及地下水水文学[16]方面都有比较广泛的应用。根据以上研究成果,本文使用Gslib程序库中的序贯高斯模拟程序和序贯指示模拟程序作为随机场生成器与MODFLOW进行耦合。
1 MODFLOW-Gslib工作原理 1.1 MODFLOW中的数据读取MODFLOW-2005[17]程序由Fortran语言编写,设计结构的最大特点是模块化,它包括一个主程序和若干个相对独立的子程序包(package),每个程序中有数个模块,各个模块用以完成数值模拟的一部分。
在MODFLOW-2005的运行过程中,对于二维实数型数组数据的读取一般调用实用子程序U2DREL。数组的外部输入标志有恒定值(CONSTANT)、内部输入(INTERNAL)、外部输入(EXTERNAL)和从文件中打开(OPEN/CLOSE)。在MODFLOW-2005运行过程中遇见这4种标志时,会对数据做相应处理,通过这种方式能够实现对用户输入数据的读取和重新分配。在用户输入某一区域的数据时,软件均采取均匀分布的方式将数据分布于各水文地质单元体中,但这种模型的简化方式在实际中与水文地质参数可能出现的空间变异性分布不相符。
1.2 MODFLOW-Gslib软件工作原理针对以上不足,本文基于MODFLOW-2005软件的Fortran源代码,重新编写U2DREL子程序,将MODFLOW与Gslib程序库中的随机模拟程序序贯高斯模拟(SGSIM)和序贯指示模拟(SISIM)进行嵌套,开发了MODFLOW-Gslib软件(以下简称M-G软件)。
在MODFLOW-2005中,水文地质参数一般通过BCF6包(block-centered flow 6 package)或LPF包(layer property flow package)输入,M-G软件的输入格式与MODFLOW-2005基本相同。但M-G软件在MODFLOW-2005中CONSTANT、INTERNAL、EXTERNAL和OPEN/CLOSE 4种输入标志的基础上,添加了SGSIM、SISIM、LOGSGS和LOGSIS 4种标志,分别代表对参数实现一次序贯高斯分布、序贯指示分布、对数序贯高斯分布和对数序贯指示分布,并生成相应的二维数组。当输入的参数需要进行随机模拟反映不确定状态时,根据所需要模拟的模型类型,输入相应标志和生成文件的文件名执行随机模拟过程,随机模拟过程中生成的数据将自动带入接下来的地下水流数值模拟计算,图 1以读取标志SGSIM为例说明M-G软件运行过程。

|
| 图 1 SGSIM运行程序框图 Figure 1 Blockdiagram of SGSIM |
|
|
M-G软件生成的数据保存在用户自定义输入的文件名中,用来存储模拟生成的二维数组,便于模拟结束后对模拟生成的参数进行检验和校正。为了实现程序的运行,需准备Geo-EAS格式的参数输入文件,控制随机模拟和插值过程。
2 模型举例M-G软件可用于考虑参数不确定因素影响的地下水数值模拟中,以刻画含水层的非均质性特征。本文以一个理想的模型为例,检验软件的实用性和可操作性。
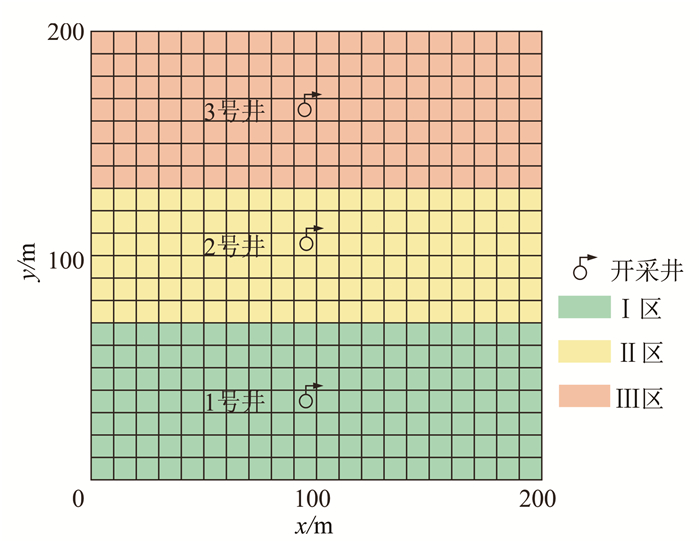
2.1 模型概况本文对一非均质各向异性含水层进行模拟。如图 2所示,模拟的含水层为一边长为200 m、水力坡度为0的正方形承压含水层,含水层厚度为10 m,储水系数为0.000 1,四周为隔水边界,模型划分为20×20单元网格,每个单元格为边长10 m的小正方形。用单元格右上角坐标代表单元格位置,记左下角第一个单元格为(1,1),分别在模型中单元格(10,4)、(10,11)和(10,17)处设3口完整井,记为1、2和3号井,以100 m3/d强度抽水,取模型中层各向异性值(HANI)为0.8。在模拟区内设3个分区,将第1—7行、第8—13行、第14—20行分别设为Ⅰ区、Ⅱ区、Ⅲ区,设0.1 d为一个应力期,观测20个应力期,即2 d内模型变化。
|
| 图 2 模型设置图 Figure 2 Initial conditions of simulation model |
|
|
如上文所述,在国内外研究中发现在地质条件相近的含水层中渗透系数一般呈对数正态分布,即渗透系数的对数可以用序贯高斯模拟反映其变异性特征。在本例中,以渗透系数的不确定性为研究对象,建立M-G模型。在使用M-G软件模拟的过程中,针对不同分区问题,采用先在研究区整体内生成一组符合序贯高斯分布的模拟值,再与输入文件中MULT文件(multiplier array file)中的数组结合,针对不同分区进行缩放,实现参数分区的方法。过程中作为基数的渗透系数K以10 m/d为均值,K的对数服从大小为2.000 0~2.605 2、方差为0.008的正态分布。模型中,Ⅰ区、Ⅱ区、Ⅲ区渗透系数的均值分别为10、20、30 m/d。即MULT文件中1—7行数值均为1,8—13行数值均为2,14—20行数值均为3。
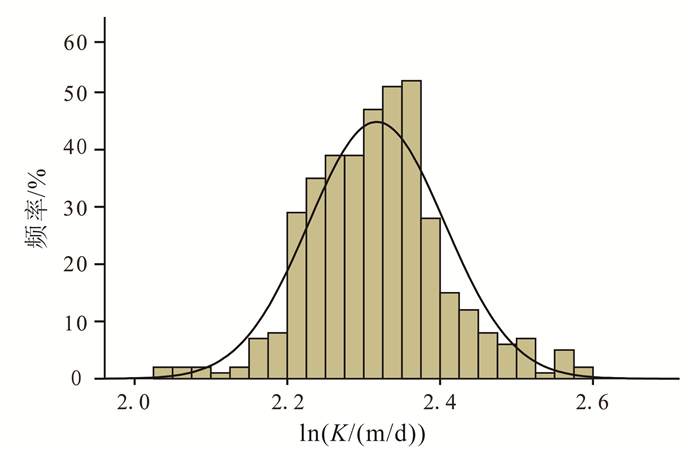
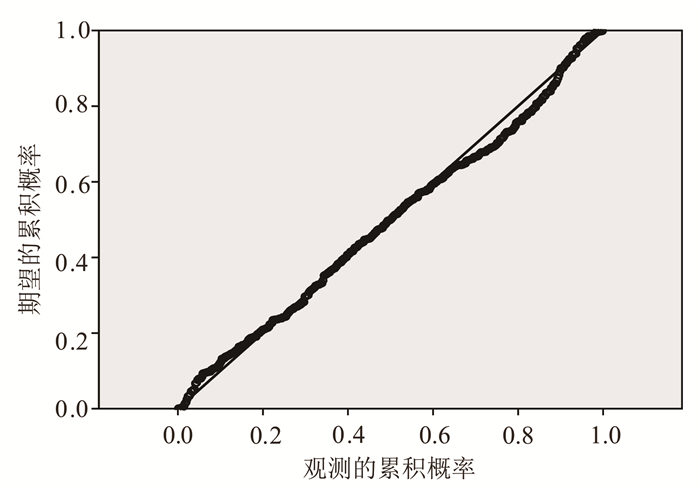
2.2 M-G模拟结果分析使用SPSS软件,对模拟后生成的数据进行数据分析。对模拟产生的K值取对数绘制频率分布直方图(图 3)和正态P-P(P为概率)图(图 4),可以看出,图像从直观上符合正态分布;再进一步对样本数据进行统计分析,得到相关参数如表 1所示,其中偏度为0.190 7、峰度为0.841 5。这表明拟合结果分布形态与正态分布相似,进一步说明模拟中所使用的渗透系数服从对数正态分布。
|
| 图 3 频率分布直方图 Figure 3 Frequency distribution histogram |
|
|
|
| 图 4 正态P-P图 Figure 4 Normal probability plot |
|
|
| 均值 | 均值的95%置信区间 | 中值 | 方差 | 标准差 | 极小值 | 极大值 | 范围 | 偏度 | 峰度 | ||
| 下限 | 上限 | ||||||||||
| 统计量 | 2.317 0 | 2.308 3 | 2.325 8 | 2.317 0 | 0.007 9 | 0.089 0 | 2.033 2 | 2.590 8 | 0.557 7 | 0.190 7 | 0.841 5 |
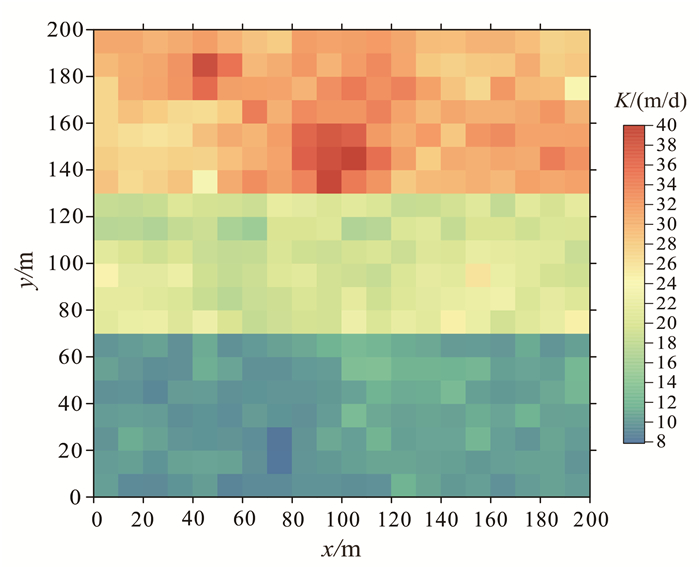
在二维空间中,渗透系数值在含水层中的空间分布如图 5中所示,在模型的模拟过程中能将样本随机分布在模拟区内,符合区域的变异性特征。
|
| 图 5 渗透系数值2-D分布图 Figure 5 Distribution map of 2-D of hydraulic conductivity |
|
|
为了更好地验证M-G软件在模拟中的作用,另使用MODFLOW-2005软件建立对照模型。对照模型中,渗透系数在各分区内均匀分布,即对应的第1—7行、第8—13行、第14—20行,K分别取10,20,30 m/d。比较模拟结果中第20个应力期内迭代的最大水头变化和单元体内水量的最大变化量所在位置,结果如表 2所示。
| 位置 | 最大水位变化量/m | 最大水量变化量/m3 | |
| MODFLOW模拟结果 | (10,4) | 0.068 | 0.042 |
| M-G模拟结果 | (10,4) | 0.069 | 0.045 |
从模拟结果对比中可得,使用M-G软件模拟时,最大水位、最大水量变化出现的位置均与使用MODFLOW模拟时的模拟结果相同,即在开采井中心位置水位降深最大,这体现了M-G软件的可靠性。
而在开采井中心位置最大水位、最大水量变化量的大小不同,表现出与MOFLOW模拟结果的差异性,这种差异性是由于M-G软件建立的模型考虑到参数存在的不确定性引起的。
两种模拟过程中,由于各水文地质单元体的渗透系数在模拟中各不相同,数值模拟计算所得的各单元体内水头变化也不同,且随着时间增长这种差异越明显。图 6分别列举了第5、10、15、20个应力期末的水头变化情况。

|
| 图 6 第5、10、15、20个应力期末两种模拟结果水位降深变化对比 Figure 6 Simulation results comparison chart of water level at the end of the 5, 10, 15, 20 stress periods |
|
|
由于Ⅰ区、Ⅱ区以及Ⅲ区渗透系数依次增大,因此3个开采井在同时开采过程的不同阶段,等水位线的变化各不相同,由此可得到开采漏斗形态的变化规律。在渗透系数最大的3号井附近,开采漏斗变化响应最快,两种模拟软件在模拟初期就表现出开采漏斗形态差异。如图 6a中,M-G软件模拟得到的0.05 m等水位降深线形状更扁圆,漏斗中心处水位降深达到0.40 m,大于MODFLOW模拟的0.30 m。这是由于渗透系数的非均质性引起的水位变化局部差异性,与温忠辉等[18]在开采量的不确定性研究中的结论更为相符。而在渗透系数较小的1号井附近,开采引起的降落漏斗范围不断扩大。如图 6d所示,MODFLOW模拟生成的0.05 m等水位线沿着开采井两侧完全对称,而M-G软件模拟的等水位线向开采井左侧偏移;这表明M-G软件能够从水文地质参数不确定性角度反映出含水层空间变异性的特点。
3 结论与建议1) 基于MODFLOW开源程序,运用地下水数值模拟技术与序贯模拟技术开发的M-G软件,能够实现水文地质参数不确定性特征与地质统计学的结合,从而解决数值模拟中参数变异性问题。
2) 通过一个模拟实例的运行结果表明,转化后的渗透系数符合模拟前设定的对数正态分布特征且能随机分布在模拟区的各单元格内。
3) 将M-G软件模拟结果与MODFLOW模拟结果进行对比,M-G软件能够从水文地质参数不确定性角度反映出含水层空间变异性的特点。
4) 对地下水数值模拟不确定性模拟方法的研究仍处于探索阶段,M-G软件在地下水数值模拟中的应用还有待于在实际工作实例中继续检验。
| [1] |
鲁程鹏.
含水介质非均质性特征与效应研究[M]. 北京: 中国水利水电出版社, 2013.
Lu Chengpeng. Study on the Identification of the Heterogeneity of Aquifers and Its Effects[M]. Beijing: China Water Resources and Hydropower Press, 2013. |
| [2] |
王超, 束龙仓, 鲁程鹏. 渗透系数空间变异性对低渗透地层中地下水溶质运移的影响[J].
河海大学学报(自然科学版), 2014, 42(2): 137-142.
Wang Chao, Shu Longcang, Lu Chengpeng. Effects of Spatial Variability of Permeability Coefficient on Groundwater Solute Transport in Low Permeability Formation[J]. Journal of Hohai University (Natural Science Edition), 2014, 42(2): 137-142. |
| [3] |
马荣, 石建省, 刘继朝. 人工内分泌网络模型在水文地质参数研究中的应用[J].
吉林大学学报(地球科学版), 2013, 43(3): 914-921.
Ma Rong, Shi Jiansheng, Liu Jichao. Application of Artificial Endocrine Network Model in Hydrogeological Parameters[J]. Journal of Jilin University (Earth Science Edition), 2013, 43(3): 914-921. |
| [4] | Lu C, Chen X, Cheng C, et al. Horizontal Hydraulic Conductivity of Shallow Streambed Sediments and Comparison with the Grain-Size Analysis Results[J]. Hydrological Processes, 2012, 26(3): 454-466. DOI:10.1002/hyp.v26.3 |
| [5] | Elsheikh A H, Wheeler M F, Hoteit I. Nested Samp-ling Algorithm for Subsurface Flow Model Selection, Uncertainty Quantification, and Nonlinear Calibration[J]. Water Resources Research, 2013, 49(12): 8383-8399. DOI:10.1002/2012WR013406 |
| [6] |
卞建民, 刘彩虹, 杨晓舟. 吉林西部大安灌区土壤贮水能力空间变异特征及土壤水分有效性[J].
吉林大学学报(地球科学版), 2017, 47(2): 554-563.
Bian Jianmin, Liu Caihong, Yang Xiaozhou. Spatial Variation of Soil Water Storage Capacity and Soil Water Availability in Da'an Irrigation District, West Jilin Province[J]. Journal of Jilin University (Earth Science Edition), 2017, 47(2): 554-563. |
| [7] |
王开丽, 黄冠华. 强变异渗透系数对地下水和溶质迁移影响的模拟研究[J].
水动力学研究与进展:A辑, 2010, 25(4): 542-550.
Wang Kaili, Huang Guanhua. Study on the Effect of Strong Variation Permeability Coefficient on Groundwater and Solute Transport[J]. Journal of Hydrodynamics Research and Progress:Series A, 2010, 25(4): 542-550. |
| [8] |
刘爱利, 王培法, 丁园圆.
北京:地统计学概论[M]. 北京: 科学出版社, 2012.
Liu Aili, Wang Peifa, Ding Yuanyuan. Beijing:Introduction to Geostatistics[M]. Beijing: Science Press, 2012. |
| [9] |
张延凯, 李克庆, 杨诗海, 等. 地质统计学储量估算中块尺寸的合理选择[J].
吉林大学学报(地球科学版), 2017, 47(1): 106-112.
Zhang Yankai, Li Keqing, Yang Shihai, et al. Reasonable Selection of Block Size in Estimating Geostatistical Reserves[J]. Journal of Jilin University(Earth Science Edition), 2017, 47(1): 106-112. |
| [10] |
施小清, 姜蓓蕾, 卞锦宇, 等. 以地质统计方法推估上海第三承压含水层渗透系数的分布[J].
工程勘察, 2009, 37(1): 36-41.
Shi Xiaoqing, Jiang Beilei, Bian Jinyu, et al. Distributed in Geostatistical Method to Calculate a Third Shanghai in Under Pressure Aquifer[J]. Engineering Investigation, 2009, 37(1): 36-41. |
| [11] |
王艳妮, 谢金梅, 郭祥. ArcGIS中的地统计克里格插值法及其应用[J].
软件导刊, 2008(12): 36-38.
Wang Yanni, Xie Jinmei, Guo Xiang. Geostatistical Kriging Method and Its Application in ArcGIS[J]. Software Guide, 2008(12): 36-38. |
| [12] |
岳松梅, 杨蕴, 吴剑锋, 等. 基于不同地质统计方法的渗透系数场对污染物运移的影响[J].
地下水, 2014(4): 10-14.
Yue Songmei, Yang Yun, Wu Jianfeng, et al. Effects of Permeability Coefficient Field on Pollutant Transport Based on Different Geological Statistics[J]. Groundwater, 2014(4): 10-14. |
| [13] | Deutsch, Clayton V. GSLIB Geostatistical Software Library and User's Guide[M]. Oxford: Oxford University Press, 1992. |
| [14] |
张晓坤. 随机模拟在三维地质建模中的应用[D]. 北京: 中国地质大学, 2009.
Zhang Xiaokun. Application of Stochastic Simulation in 3D Geological Modeling[D]. Beijing:China University of Geosciences, 2009. http://d.wanfangdata.com.cn/Thesis/Y1782522 |
| [15] |
王英伟, 张建民, 王满, 等. 基于序贯指示模拟方法的火山岩储层岩性及孔隙度模拟[J].
吉林大学学报(地球科学版), 2010, 40(2): 455-460.
Wang Yingwei, Zhang Jianmin, Wang Man, et al. Characteristics of Lithology and Porosity of Volcanic Reservoirs Based on Sequential Instruction Simulation Method[J]. Journal of Jilin University (Earth Science Edition), 2010, 40(2): 455-460. |
| [16] |
张飞, 温忠辉, 戴凤君, 等. 基于渗透系数序贯高斯模拟的水库渗漏量不确定性分析[J].
水资源保护, 2016, 32(3): 69-73.
Zhang Fei, Wen Zhonghui, Dai Fengjun, et al. Netermination of Reservoir Leakage Based on Sequential Gaussian Simulation of Permeability Coefficient[J]. Water Resources Protection, 2016, 32(3): 69-73. DOI:10.3880/j.issn.1004-6933.2016.03.013 |
| [17] | Harbaugh A W. MODFLOW-2005, the US Geolo-gical Survey Modular Groundwater Model:The Groundwater Flow Process[J]. Center for Integrated Data Analytics Wisconsin Science Center, 2005. |
| [18] |
温忠辉, 曹英杰. 开采量不确定条件下数值模拟结果的可靠性分析[J].
吉林大学学报(地球科学版), 2007, 37(2): 239-242.
Wen Zhonghui, Cao Yingjie. Reliability Analysis of Numerical Simulation Results in the Exploitation of Uncertainty[J]. Jilin University (Earth Science Edition), 2007, 37(2): 239-242. |


