2. 天津大学滨海土木工程结构与安全教育部重点实验室, 天津 300072
2. Key Laboratory of Coast Civil Structure Safety of Education Ministry, Tianjin University, Tianjin 300072, China
0 引言
随着我国国民经济的迅速发展,沿海地区用地紧张态势日益严重,利用航道疏浚淤泥进行吹填造陆成为被广泛采用的方法[1-2]。由于高黏性新近吹填淤泥处于“稀泥汤”状态,工程特性极差,几乎无承载力[3],目前主要采用各类改进的真空预压技术对其进行加固[4-7]。工程实践表明,由于颗粒组成不同,吹填土真空加固效果明显不同,如:黏粒含量较高的吹填土固结情况和力学性质相对较差[8];另外,在同一片吹填场区,由于距离吹填口的远近不同,吹填土颗粒组成不同,也造成了整个场地处理效果呈现不均匀的现象。因此,研究颗粒组成对真空预压加固处理效果的影响特点有一定工程意义。
对于真空预压法的分析评价可通过现场测试、室内模型试验、有限元数值模拟等手段进行研究。陈平山等[9]对现场进行了孔压监测和静力触探试验,通过分析距排水板不同位置土体的孔压变化、强度变化,指出“土桩”是排水板周围土体细颗粒在渗透力作用下向排水板聚集的结果;颜永国等[10]进行了不同颗粒级配试样的真空预压室内模型试验,结果表明不同的颗粒级配对沉降量、排水量和加固后物理力学性质有显著影响;武亚军等[2]考虑加载方式的影响开展了室内模型试验,得出了初始真空荷载越大,土颗粒移动趋势越明显,土颗粒会聚积在排水板周围而导致土体渗透性能的降低等规律;阮昆[11]利用有限元软件ABAQUS对真空预压过程进行模拟,对比分析了不同施工条件下的加固效果,提出了一些改善加固效果的措施,如减少排水板打设间距。
综上可知,已有的研究主要集中在宏观层次上,而微观层次研究较少,还不成熟,总体上国内外在吹填场区超软土地基这方面均缺乏足够的研究。随着基础设施的不断兴建,施工及服役期间所引起的工程问题将会日益突出,对吹填场区的地基处理过程进行充分认识和正确模拟,进而揭示和认识荷载作用下软土的变形机理和本质,无论是从学术和科研的角度,还是从工程建设的发展和要求来看,都具有较重要的实际意义。
颗粒流软件可以从微观角度分析大变形问题,可以模拟颗粒的移动。近些来,有不少学者将其用于真空预压法的模拟。习志雄[12]基于PFC2D模拟土颗粒的运动,定性研究了不同工况下排水板间距、排水真空度和土体原始孔隙率等因素对土体孔隙率的影响,得出原始孔隙率越小的土体真空排水预压后土体越均匀,大孔隙率的土体真空预压后各区域土体分布极不均匀等结论;宋晶[13]建立了三维颗粒流数值模型对大连地区高黏性吹填土分级真空预压固结过程进行模拟,证实了分级真空预压工法的可行性;武亚军等[14]和邹燃[15]分别做了真空预压法处理地基的相关模拟,对真空预压过程土体变形机理进行了研究。以上这些模拟都是通过改变外部条件如加载方式对真空加固效果进行研究,基于土体自身特性变化的影响分析尚缺乏系统深入的模拟研究。
本文首先依托天津临港经济区T7新近吹填区地基加固工程进行直排式真空预压法室内模型试验,并采用颗粒流软件PFC2D对模型试验进行模拟计算和规律分析,对比室内试验和模拟计算结果,验证计算方法的可靠性;然后进行6组不同颗粒组成吹填土真空预压试验的颗粒流微观模拟,总结排水速率变化及颗粒运移规律,从宏观和微观角度探讨不同土样淤堵层形成机理和加固效果影响规律。
1 室内模型试验概况依据天津临港经济区工程现场直排式真空预压法工艺流程进行室内模拟试验,保证方法的有效性。
1.1 试验简介室内试验所采用的吹填淤泥取自天津临港经济区T7新近吹填区。试验前将土样烘干、筛除土中杂质、加入适量水使其处于流塑状态,然后将配置好的土样放入试验槽中,再加入适量水搅拌均匀,使其含水量达到200%左右,与现场新近吹填土表层浮泥含水率保持一致。土样经过实验室重新调制后的颗分曲线如图 1所示;其基本物性指标为:比重2.75、孔隙比4.6、含水率204.5%、塑性指数29.2%、液性指数63.8%、粉粒质量分数31.3%、黏粒质量分数68.6%。

|
| 图 1 试验土样颗分曲线 Figure 1 Particle analysis curve of test soil samples |
|
|
从前文和图 1可知,该吹填淤泥土样具有以下特点:1)颗粒细,含有大量黏粒,黏粒质量分数达到总颗粒的70%左右;2)液限高,塑性指数大于25.0%,为高塑性淤泥质黏性土;3)含水率高,在150.0%以上;4)孔隙比大(e>2.4)。根据《港口工程地基规范》,可判定该土样为浮泥,是一种无结构强度、无附着力、处于悬浮状态的工程性质极差的土样,符合工程实际[7]。
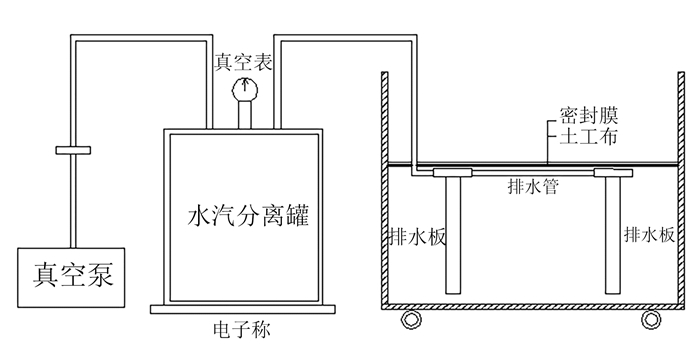
根据现场实际工况进行了室内真空预压排水法固结试验设备的设计,设备装置如图 2所示。试验设备包括排水系统、量测系统和模型槽;排水系统包括真空泵、排水板、排水管和水汽分离罐;量测系统包括真空表、电子称等;模型槽由钢化玻璃制成,尺寸为100 cm×80 cm×70 cm(长×宽×高)。
|
| 图 2 室内模型试验装置示意图 Figure 2 Test model and measuring equipment installations |
|
|
调制好后的土样,经过静置一段时间之后会出现水土分离现象,所以试验是在经过12 h的自重固结之后取出表层水再进行插板排水,此时土层高度为45 cm,计算得出土体孔隙比由初始的4.6下降为4.0。排水板插入土体深度30 cm,间距50 cm。插板之后,在其上依次铺设土工布和密封膜并在周边密封,然后施加真空荷载-80 kPa,在加载排水过程中对排水量随时间的变化进行监测,当排水量达到稳定值时试验结束。
1.2 试验结果分析为了更清楚地反映排水过程中排水速率的变化规律,将时间(t)取对数,此时排水速率变化规律如图 3所示。由图 3可知:排水过程中排水速率先是快速上升达到最高点,这个阶段时间较短;接着排水速率开始逐渐下降,下降到一定程度曲线开始逐渐趋于平稳,这个阶段时间较长;最后排水速率缓慢下降并逐渐趋向于0。根据排水速率变化特点可将排水阶段划分为排速上升、排速下降、排速平稳3个阶段。

|
| 图 3 排水速率随时间变化曲线 Figure 3 Curve of drainage rate with 14:08:41 |
|
|
排速上升阶段,细颗粒不断流失,未形成淤堵层,因此排水速率快速提高并达到峰值,本次试验排水速率峰值为0.008 kg/min。排速下降阶段,随着排水板表层颗粒不断黏附堆积,淤堵层开始形成,排水速率开始呈现快速下降的趋势,直到速率趋于平稳。本文图 3曲线切线斜率为0.001时对应的时间为此阶段结束时间,这个阶段经历时间是快速排水阶段经历时间的2倍左右,最低速率大约为排水速率峰值的1/10,排水量约为排水上升阶段的4倍;因此这个阶段也可称为主要排水阶段。排速平稳阶段,淤堵层完全形成,排水速率缓慢趋近于0,排水固结过程基本结束。
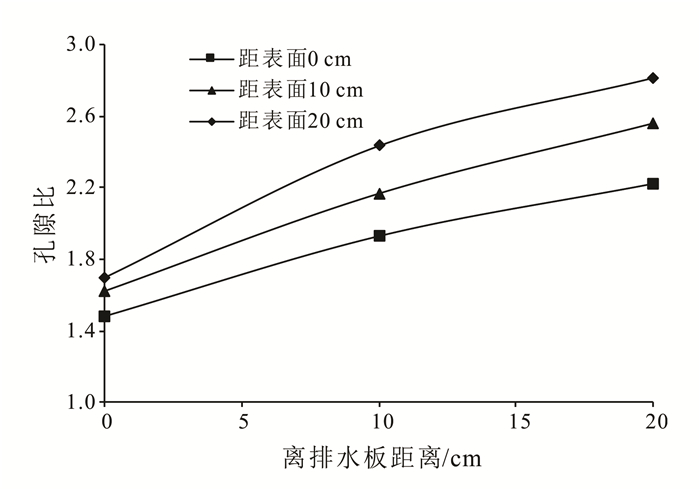
排水完成后,对离排水板不同距离、不同深度的土体进行取样,测量其孔隙比,不同位置处土体孔隙比分布如图 4所示。从图 4可看出:同一深度处,离排水板距离越远的土体孔隙比越大,离排水板相同水平距离处的土体,随着深度的增加孔隙比逐渐增大。这与土体中真空度传递规律[8]一致,即真空度随着土体深度、离排水板距离的增加不断消减,因此排水效果越差,土体孔隙比越高。
|
| 图 4 不同位置的土体孔隙比 Figure 4 Void ratio of soil in different locations |
|
|
采用颗粒流软件PFC2D对上述真空预压室内模型试验进行模拟,将颗粒流计算分析结果与室内试验分析结果进行对照,验证颗粒流计算分析结果的正确性并分析淤堵层形成机理。
2.1 模型建立与参数选取模型是由球体和墙体组成的,球体代表土颗粒,墙体代表水头边界。在真空压力作用下,孔隙水主要沿水平方向渗流,2个排水板之间的土颗粒主要受到水平方向的渗流力和竖向的自重力作用,因此可取沿2个排水板连线的剖面(图 2)作为模拟平面,模型可简化为一个矩形平面。忽略竖向排水,矩形的上下边为不透水边界,左右边可认为是排水板边界。
排水板为对称布置并根据其影响范围控制了井径比,因此个2排水板之间的土体单元为左右对称单元,可取一半进行分析,对称处可认为是不透水边界。取排水板间距的一半作为左右墙体的间距,排水板入土有效深度作为上下墙间距。为了防止颗粒数目过大影响计算效率,模型尺寸按照比例缩小,最终确定模型尺寸为水平0.25 cm、竖向0.30 cm,并且对图 1所示颗粒级配最小粒径进行修正,取最小粒径为0.004 mm。
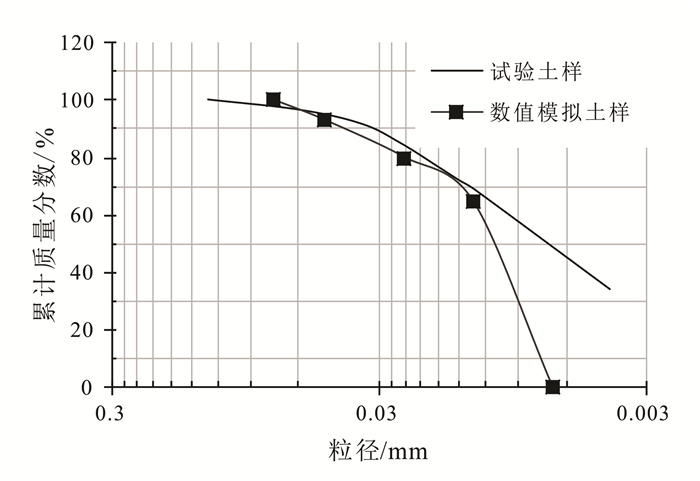
生成土颗粒时,需要将室内试验土样的颗粒级配、孔隙比进行转换。本文参考徐国建等[16]提出的非等粒径转换方法:首先根据各粒组质量分数及粒组平均粒径计算出二维情况下相应粒组颗粒数目的基本比例;然后综合考虑颗粒总数设定某一粒组的颗粒数目,并代换计算得到最终各粒组颗粒数目。孔隙比换算通过颗粒半径放大因子进行粒径修正,以得到与试验真实孔隙比对应的孔隙比。经过换算,此数值模型需将土粒粒径放大2.68倍,放大后的等效二维孔隙比为2.43。为了便于试验模型与数值模型级配曲线对比,将试验土样级配曲线粒径也放大2.68倍,级配曲线图如图 5所示,颗粒数为10 925。由图 5可知,级配曲线与试验用土级配曲线基本一致。
|
| 图 5 试验土样及数值试样颗分曲线 Figure 5 Particle analysis curve of tested samples |
|
|
排水板滤膜的孔隙状态是决定排水性能最重要的因素,如何反映滤膜的孔隙特征是模拟排水板的关键。由压汞法及干筛法测得室内试验所用的排水板滤膜孔洞排列较规则,滤膜的平均孔径约为0.03 mm,因此可采用一系列间距为0.03 mm的点墙来模拟排水板。本文将数值模型的左边界设置成点墙,通过设置负的流体压力模拟真空负压,上下边界设置为整墙,作为不透水边界。
真空预压渗流过程是真空流体和土颗粒相互作用的过程,需要在土颗粒单元四周设置流体单元,形成流体网格来实现流固相互作用。每个流体网格和网格中的颗粒组成一个流体计算单元,固相计算和流固计算交替进行。经多次试算,本模型最终确定流体单元数为120(10×12)个。数值模拟过程中,通过将点墙边界处流体单元的流体压力设置为-800 Pa(缩小100倍),右侧墙体位置处流体单元的流体压力设为0,来实现对整个土体施加真空压力。
颗粒流模型的宏观特性由组成模型的颗粒和墙体的微观参数决定,颗粒材料强度参数和变形参数决定着物理力学模型的宏观力学响应和变形特性。本文根据李坤蒙等[17]提出的PFC2D数值计算模型微观参数确定方法对数值模拟材料参数进行标定,参数如表 1所示。由表 1可知,对黏粒赋予了黏结强度,目的是使不断聚集接触的黏粒通过粘结作用形成“假粉粒”团聚体[12]。
| 材料 | 比重 | 法向刚度/(107N/m) | 切向刚度/(105N/m) | 法向黏结强度/N | 切向黏结强度/N | 摩擦因数 | 黏滞系数/(10-3Pa·s) |
| 黏粒 | 2.75 | 1.0 | 1.0 | 1 000 | 500 | 0.5 | — |
| 粉粒 | 2.75 | 1.0 | 1.0 | — | — | 0.5 | — |
| 墙 | — | 100.0 | 1.0×104 | — | — | 0.7 | — |
| 水 | 1 000.00 | — | — | — | — | — | 1.0 |
模型计算简图如图 6所示。由图 6可知,颗粒按照所在位置不同区分了颜色,便于观察颗粒运移前后位置变化。颗粒初始状态与所模拟的吹填浮泥特征一致,颗粒处于悬浮状态,土体基本没有承载力。

|
| 图 6 颗粒流模拟模型 Figure 6 Particleflow model for simulation |
|
|
软件模拟过程中以点墙处边界流网流体流速作为排水速率,当排水速率趋于0时可以认定排水固结阶段基本完成,排水板外部完全形成淤堵。
图 7为排水结束时的模型颗粒分布状态。图 7中排水板附近形成了密实的淤堵层,形状与工程现场的“土桩”[9]相似;靠近排水板土体沉降较小,远离排水板土体沉降较大,这与室内试验和工程现场土体沉降规律基本一致。

|
| 图 7 颗粒分布最终状态 Figure 7 Final particle distribution |
|
|
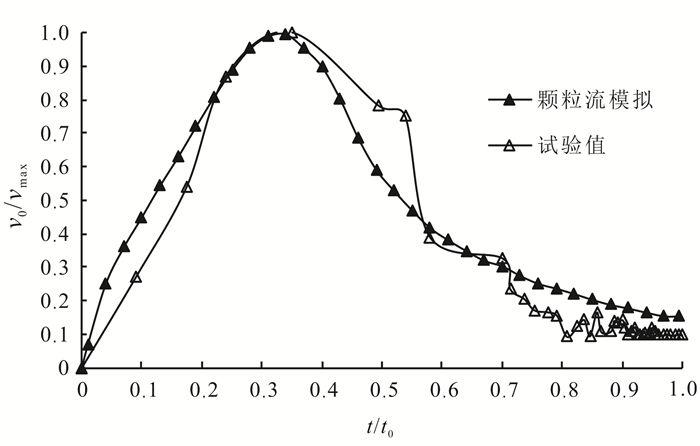
为了证明数值模拟过程中排水速率变化规律与室内试验一致,对室内试验排水对数时间、排水速率和数值模拟的时间、排水速率分别做最大值归一化处理[18],得出各自的排水速率变化曲线如图 8所示。
|
| v0.排水速率;vmax.最大排水速率;t0.总排水时间。 图 8 排水速率试验与数值模拟对比 Figure 8 Comparison of drainage rate between test and simulation results |
|
|
从图 8可看出,数值模拟过程中排水速率的变化规律与室内试验基本吻合,排水速率变化过程都可分为快速增长阶段、快速下降阶段及稳定阶段,且各阶段时长占排水总时长的比例二者也相同。
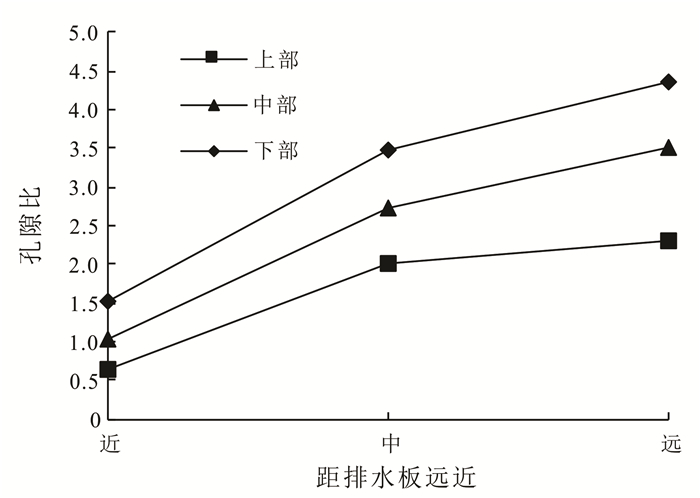
排水结束后,对数值模型不同位置的土体孔隙比进行统计,孔隙比分布如图 9所示,图中上、中、下部为沿土体深度方向平均取3点所确定,3点间距相同。与图 4所示的室内试验孔隙比分布图对比,虽然取样点的差异数值上有些差别, 但是发现二者呈现相同的分布规律:同一深度处,离排水板距离越远的土体孔隙比越大;离排水板相同水平距离处的土体,随着深度的增加孔隙比逐渐增大。
|
| 图 9 数值模型不同位置的土体孔隙比 Figure 9 Void ratio of soil in different locations |
|
|
综上所述,在选取适当参数的情况下,本文的计算模型和参数选取可以对不同颗粒组成条件下的真空预压加固处理进行有效模拟。
2.3 淤堵层形成机理分析颗粒在运移过程中不断聚集在排水板周围,逐渐形成一层柱状淤堵层,淤堵层的力学特性变化过程反映了淤堵层形成规律。图 10为颗粒运移过程中淤堵层接触力链变化过程,每隔2万时步记录一次。

|
| 蓝色线条表示颗粒间的接触压力,红色线条表示接触拉力,黑色线条表示颗粒之间存在的接触。 图 10 淤堵层接触力链变化过程 Figure 10 Change process of clogging layer |
|
|
由图 10可知,在整个过程中接触力链首先在局部区域形成,随着黏粒不断聚集,颗粒配位数迅速增加,接触力链不断扩展延伸形成完整的力链网。力链网形成的过程也是颗粒间孔隙不断被填补的过程,开始阶段颗粒在排水体局部聚集,形成许多长而宽的渗流路径;随着孔隙不断被细颗粒填补形成致密淤堵层,排水路径变得短窄,排水效率大大降低。
3 不同颗粒组成试样的颗粒流模拟 3.1 数值模拟方案为了研究颗粒组成对真空预压固结效果的影响,设置了6组不同级配试样,如表 2所示。图 11为对应的颗粒级配曲线。各级配最小粒径一致,最大粒径及各粒组质量分数均有所差别,相邻两组试样(A与B、C与D、E与F)的颗粒不均匀系数相同。本文主要针对天津地区高黏性吹填淤泥进行研究,其粒径小于0.075 mm的颗粒占98%以上,因此本数值模拟方案最大颗粒粒径不超过0.075 mm。
| 试样 | wB/% | 等效孔隙比 | 不均匀系数 | 颗粒数 | 最大粒径/mm | |
| 黏粒 | 粉粒 | |||||
| A | 60 | 40 | 2.46 | 2.78 | 11 847 | 0.020 |
| B | 55 | 45 | 2.49 | 2.78 | 11 883 | 0.030 |
| C | 50 | 50 | 2.42 | 3.77 | 12 115 | 0.040 |
| D | 45 | 55 | 2.44 | 3.77 | 12 346 | 0.050 |
| E | 40 | 60 | 2.41 | 5.69 | 12 682 | 0.060 |
| F | 35 | 65 | 2.40 | 5.69 | 13 119 | 0.075 |

|
| 图 11 6组数值试样级配曲线 Figure 11 Grain-size distributions of numerical samples |
|
|
数值方案中模型的微观参数的获取采用与上述验证试验模型相同的方法。
为了比较不同级配试样在相同条件下的排水效果,对各试样在排水过程中的排水速率进行记录,直到排水速率趋近于稳定,排水固结结束。
3.2 颗粒运移特点分析排水结束后,各试样变形状态如图 12所示。从图 12可知:6组试样在真空预压过程中排水板周围均出现了不同程度的淤堵现象,最终形成不同厚度的柱状体淤堵层;从试样A到试样F,淤堵层厚度依次递减,即试样黏粒质量分数越大,淤堵层厚度越大。

|
| 图 12 6组试样最终变形图 Figure 12 Final deformation of soil during drainage stage |
|
|
对每个试样的淤堵层柱状体各粒径范围内颗粒占总颗粒的质量分数进行统计,如表 3所示。由表 3可知,淤堵层中小于0.005 mm的颗粒质量分数远高于其他较大粒径颗粒质量分数,这说明淤堵是由细颗粒的不断聚集造成的,细颗粒越多越容易造成排水板淤堵。
| % | ||||
| 试样 | <0.005 mm | 0.005~0.010 mm | 0.010~0.020 mm | 0.020~0.075 mm |
| A | 65 | 14 | 21 | 0 |
| B | 57 | 15 | 13 | 15 |
| C | 54 | 14 | 15 | 17 |
| D | 48 | 16 | 13 | 22 |
| E | 43 | 15 | 14 | 28 |
| F | 47 | 20 | 15 | 18 |
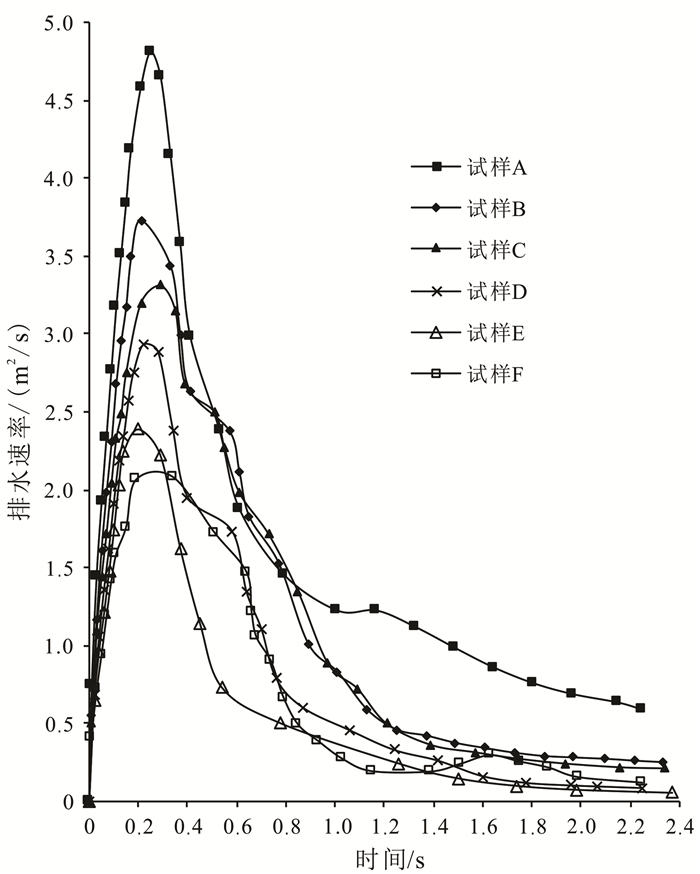
为了满足真空预压法处理新近浅层吹填土快速节能的工程需要,排水过程中既要保证较高的排水速率,又要使其持续较长的时间。根据上文对排水速率变化3个阶段的分析,排速下降阶段即主要排水阶段对排水效率的影响最大,这个阶段排水速率越快、持续时间越长,则排水效率越高。因此对主要排水阶段的排水速率和排水时间的研究至关重要。图 13为6组试验排水固结过程中排水速率对比图,横坐标时间为计算步长乘以运行步数,由于数值模型与实际模型尺寸相差很大,因此与图 3对应时间相差很大。
|
| 图 13 6组试样排水速率图 Figure 13 Drainage rate during drainage stage |
|
|
表 4统计了6组试样主要排水阶段的时间、最高排水速率及最低排水速率。图 13中,当排水速率达到最高排水速率的10%左右时,6组试样的排水速率曲线都基本趋于平稳。因此,为了便于分析,取最高排水速率的10%作为主要排水阶段的最低排水速率。
| 试样 | 最高速率/(m2/s) | 最低速率/(m2/s) | 主要排水阶段时间/s |
| A | 4.808 | 0.481 | >1.73 |
| B | 3.732 | 0.373 | 1.38 |
| C | 3.316 | 0.332 | 1.12 |
| D | 2.930 | 0.293 | 1.10 |
| E | 2.392 | 0.239 | 0.98 |
| F | 2.061 | 0.206 | 0.95 |
如前所述,排水过程的第一阶段排水速率达到最高,最高排水速率从试样A到试样F呈明显下降趋势,即黏粒质量分数越大的试样最高排水速率越大。这个阶段土颗粒和水在真空压力作用下共同向排水板加速运动,细小颗粒不断随水流排出,因此黏粒质量分数越大加速作用越明显。
模拟时间结束时,试样A的排水速率仍有明显下降趋势,可以判定淤堵层尚未完全形成,尚未进入第三排水阶段;而其他几组试样在模拟时间内排水速率都降到了很低水平,都进入了第三排水阶段。结合表 2可知出现这种结果的原因可能与试样最大粒径有关。试样A的最大颗粒粒径为0.020 mm,小于排水板滤膜孔径0.030 mm,而其余试样的最大颗粒粒径都比排水板滤膜孔径大;另外,试样F在达到最低排水速率后,排水速率出现反弹且上下波动的现象,可能与试样F的黏粒质量分数较小、无法对粉粒形成良好的黏结包裹作用导致淤堵层不稳固有关。
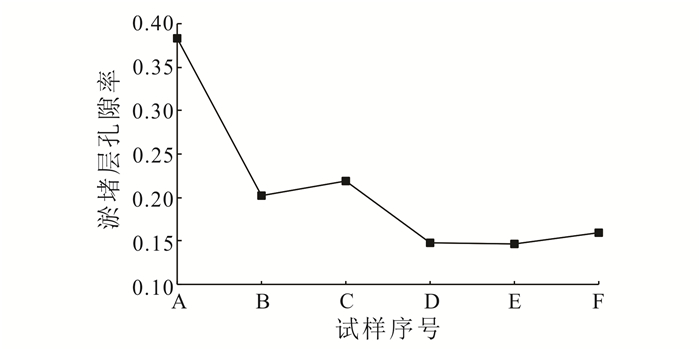
3.3.2 主要排水阶段时间及淤堵层对比表 4中的主要排水阶段时间可发现,从试样A到试样F主要排水阶段的时间依次减少。试样A由于最大粒径小于排水板滤膜孔径,主要排水阶段时间远大于其余试样。其余各组试样的主要排水阶段时间在不均匀系数不同时差别更明显。对6组试样第二排水阶段结束时淤堵层孔隙率进行统计,结果如图 14所示。试样A淤堵层孔隙率最大,其他几组试样淤堵层孔隙率明显降低,形成更加密实的淤堵层,排水条件较差;试样B和C的淤堵层孔隙率相当;试样D、E和F的淤堵层孔隙率相当,但相对试样B和C又有明显下降。因此,颗粒组成影响淤堵层的形成,从而影响主要排水阶段的时间,土体的不均匀系数越高,淤堵层形成越快,主要排水阶段的时间越短。
|
| 图 14 6组试样淤堵层平均孔隙率 Figure 14 Porosity of clogging layer |
|
|
真空预压排水固结过程有排水固结和自重固结两方面固结形式,前者主要产生横向变形,后者主要产生竖向变形,土体在两者共同作用下完成固结变形。6组试样的泥面轮廓线如图 15所示,水平和竖向孔隙率分布如图 16所示。

|
| 图 15 6组试样泥面轮廓图 Figure 15 Soil profile of six samples |
|
|

|
| 注:a中区域1、2、3分别代表距排水板0~5、5~10、10~20 cm范围;b中区域1、2、3分别代表距土体表面0~10、10~20、20~30 cm范围。 图 16 6组试样孔隙率分布图 Figure 16 Porosity distribution of six samples |
|
|
综合考虑土体竖向变形、水平方向变形、2个方向土样孔隙率大小及其分布情况等因素,对6组试样的固结效果进行分析评价。
由图 15、16可得:试样A的水平变形量明显大于竖向变形量,产生的竖向变形差异最大;水平向孔隙率1区域明显小于2、3区域,且差异最大;竖向孔隙率在3个区域内都很大且比较平均,可见其整体比较疏松。因此试样A固结变形效果最差。
随着颗粒级配发生变化,固结变形效果发生了不同程度的改善。试样B和C的水平变形和试样A相当,排水板远端土体高度明显高于试样A,这说明试样B和C竖向固结变形作用增强,沉降差异减少;水平方向上,试样B和C在区域2、3的孔隙率依然很高,但分布更加均匀;相较试样A,试样B、C的下部区域的孔隙率发生了明显下降,下部区域更密实,但上部区域仍很疏松。
试样D、E、F水平变形相较前3个试样明显减少,竖向变形相对增大,泥面轮廓曲线变得更平缓;这3组试样水平方向的3处区域孔隙率都明显降低,孔隙率分布更均匀,土体水平方向固结效果得到很大改善;3组试样竖直方向3个区域的孔隙率都发生明显下降,土体竖向固结效果得到很大改善。
4 结论与建议1) 利用二维颗粒流软件PFC2D可以对真空预压加固过程进行有效模拟,保证数值模拟排水速率变化规律及土体变形规律与室内试验一致。真空预压过程中细颗粒越多越容易造成排水板淤堵,细颗粒沿渗透路径迁移的过程中在沿途不断滞留,导致渗透路径变短变窄,最终渗透路径完全堵塞而形成淤堵泥层。
2) 颗粒组成对真空预压过程排水速率、排水时间有较大的影响。对于高黏性新近吹填淤泥,在相同真空荷载下作用下,黏粒质量分数越大,初期排水速率增长越快;土体的不均匀系数越高,淤堵层形成越快,排水速率衰减越快,主要排水阶段的时间越短,排水效率越低。另外,当排水板滤膜孔径大于填充材料最大颗粒粒径时,排水效率显著提升。
3) 颗粒组成对吹填土真空预压加固后土体变形有一定影响。对于高黏性新近吹填淤泥,在相同真空荷载作用下,黏粒质量分数越大,土体的横向变形越大,竖向变形越小;随着粉粒质量分数增大,土体不同位置的孔隙率变化越均匀,最终孔隙率也越低,尤其当粉粒质量分数大于黏粒质量分数时,真空预压加固效果有明显改善。
4) 为了改善高黏性吹填土真空预压加固效果,在选择真空预压加固方法时应重视吹填土的颗粒组成。根据不同的吹填场地选择不同的排水板,排水板的滤膜孔径应至少大于颗粒组最大粒径。黏粒含量较大的吹填土可通过添加絮凝剂使黏粒减少,或通过设计合理的吹填方式使吹填土粉粒质量分数增多,黏粒质量分数减少,并保证颗粒级配均匀。
| [1] |
赵林, 郑义, 毛国柱, 等. 天津围海造陆区吹填土氮磷的分布特征[J].
吉林大学学报(地球科学版), 2015, 45(1): 255-264.
Zhao Lin, Zheng Yi, Mao Guozhu, et al. Spatial Distribution of Nitrogen and Phosphorus in Dredger Fill at Tianjin Reclamation Land Area[J]. Journal of Jilin University(Earth Science Edition), 2015, 45(1): 255-264. |
| [2] |
武亚军, 杨建波, 张孟喜. 真空加载方式对吹填流泥加固效果及土颗粒移动的影响研究[J].
岩土力学, 2013, 34(8): 2129-2135.
Wu Yajun, Yang Jianbo, Zhang Mengxi. Study of Impact of Vacuum Loading Mode on Dredger Fill Flow Mud Consolidation Effect and Soil Particles Moving[J]. Rock and Soil Mechanics, 2013, 34(8): 2129-2135. |
| [3] |
鲍树峰, 娄炎, 董志良, 等. 新近吹填淤泥地基真空固结失效原因分析及对策[J].
岩土工程学报, 2014, 36(7): 1350-1359.
Bao Shufeng, Lou Yan, Dong Zhiliang, et al. Causes and Countermeasures for Vacuum Consolidation Failure of Newly-Dredged Mud Foundation[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(7): 1350-1359. DOI:10.11779/CJGE201407020 |
| [4] |
关云飞, 唐彤芝, 陈海军, 等. 超软土地基真空预压浅层加固现场试验研究[J].
岩土工程学报, 2011, 33(增刊1): 97-101.
Guan Yunfei, Tang Tongzhi, Chen Haijun, et al. Field Tests on Shallow Treatment of Super-Soft Ground by Vacuum Preloading Method[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(Sup.1): 97-101. |
| [5] |
董志良, 张功新, 周琦, 等. 天津滨海新区吹填造陆超软土浅层加固技术研发及应用[J].
岩石力学与工程学报, 2011, 30(5): 1073-1080.
Dong Zhiliang, Zhang Gongxin, Zhou Qi. Research and Application of Improvement Technology of Shallow Ultra-Soft Soil Formed by Dredged in Tianjin Binhai New Area[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(5): 1073-1080. |
| [6] |
董志良, 张功新, 莫海鸿, 等. 超软弱土浅表层快速加固方法及成套技术: 中国, 200810026168. 4[P]. 2008-07-23.
Dong Zhiliang, Zhang Gongxin, Mo Haihong, et al. The Improvement Method and Technology of Ultra-Soft Soil:China, 200810026168[P]. 2008-07-23. |
| [7] |
董志良, 周琦, 张功新, 等. 天津滨海新区浅层超软土加固技术现场对比试验[J].
岩土力学, 2012, 33(5): 1073-1080.
Dong Zhiliang, Zhou Qi, Zhang Gongxin. Field Comparison Test of Reinforcement Technology of Shallow Ultra-Soft Soil in Tianjin Binhai New Area[J]. Rock and Soil Mechanics, 2012, 33(5): 1073-1080. |
| [8] |
颜永国. 真空荷载下不同颗粒级配软土真空度传递规律试验研究[J].
水运工程, 2010(10): 109-112.
Yan Yongguo. Experimental Study on Vacuum Degree Transfer Law of Soft Clay of Different Grain Size Grading Under Vacuum Preloading[J]. Port & Waterway Engineering, 2010(10): 109-112. DOI:10.3969/j.issn.1002-4972.2010.10.022 |
| [9] |
陈平山, 董志良, 张功新. 新吹填淤泥浅表层加固中"土桩"形成机理及数值分析[J].
水运工程, 2012, 1: 158-163.
Chen Pingshan, Dong Zhiliang, Zhang Gongxin. Mechanism and Numerical Simulation of the "Soil Piles" in the Fresh Hydraulic Mud Fill Treated by Surface-Layer Improvement Technique[J]. Port & Waterway Engineering, 2012, 1: 158-163. DOI:10.3969/j.issn.1002-4972.2012.01.032 |
| [10] |
颜永国, 董志良, 杨昌斌, 等. 颗粒级配对真空预压法处理吹填土效果影响试验研究[J].
岩土工程学报, 2011, 33(11): 1775-1779.
Yan Yongguo, Dong Zhiliang, Yang Changbin, et al. Experimental Study on Effect of Grain Size Distribution on Improvement of Dredger Fill[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(11): 1775-1779. |
| [11] |
阮昆. 真空预压法在吹填陆域软基工程中的加固效果研究[D]. 武汉: 武汉理工大学, 2014.
Ruan Kun. The Vacuum Preloading Method in the Project of the Reclaimed Soil Soft Foundation Reinforcement Effect Research[D]. Wuhan:Wuhan University of Technology, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10497-1015000077.htm |
| [12] |
习志雄. 真空预压法处理吹填淤泥质软土地基的颗粒流数值模拟[D]. 北京: 北京交通大学, 2010.
Xi Zhixiong. The PFC Numerical Simulation of Vacuum Preloading in Improving Reclamation Sludge[D]. Beijing:Beijing Jiaotong University, 2010. http://d.wanfangdata.com.cn/Thesis_Y1781289.aspx |
| [13] |
宋晶. 分级真空预压法加固高粘性吹填土的模拟试验与三维颗粒流数值分析[D]. 长春: 吉林大学, 2011.
Song Jing. Laboratory Simulation Test and PFC3D Numerical Analysis of High Clay Dredger Fill in the Consolidation Process of Step Vacuum Preloading[D]. Changchun:Jilin University, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10183-1011098857.htm |
| [14] |
武亚军, 覃萍, 杨建波. 真空荷载下超软土固结试验及土颗粒移动数值模拟研究[J].
水运工程, 2013, 09: 116-122.
Wu Yajun, Qin Ping, Yang Jianbo. Consolidation Test and Numerical Simulation of Particles Movement to Ultra-Soft Soil Bearing Vacuum Load[J]. Port & Waterway Engineering, 2013, 09: 116-122. DOI:10.3969/j.issn.1002-4972.2013.02.026 |
| [15] |
邹燃. 天津滨海新区吹填土固结前期微观特征及沉降过程模拟研究[D]. 长春: 吉林大学, 2013.
Zou Ran. Study on the Microscopic Feature and Process Simulation of Previous Settlement Consolidation of Dredger Fill in Binhai New Area of Tianjin[D]. Changchun:Jilin University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10183-1013194214.htm |
| [16] |
徐国建, 沈扬, 刘汉龙. 孔隙率、级配参数对粉土双轴压缩性状影响的颗粒流分析[J].
岩土力学, 2013, 34(11): 3321-3328.
Xu Guojian, Shen Yang, Liu Hanlong. Analysis of Particle Flow for Impacts of Granular Parameters and Porosity on Silt's Properties under Biaxial Compression[J]. Rock and Soil Mechanics, 2013, 34(11): 3321-3328. |
| [17] |
李坤蒙, 李元辉, 徐帅, 等. PFC~(2D)数值计算模型微观参数确定方法[J].
东北大学学报(自然科学版), 2016, 37(4): 563-567.
Li Kunmeng, Li Yuanhui, Xu Shuai, et al. Method to Determine Microscopic Parameters of PFC2D Numerical Model[J]. Journal of Northeastern University, 2016, 37(4): 563-567. |
| [18] |
郑刚, 戴轩, 张晓双. 地下工程漏水漏砂灾害发展过程的试验研究及数值模拟[J].
岩石力学与工程学报, 2014, 33(12): 2458-2471.
Zheng Gang, Dai Xuan, Zhang Xiaoshuang. Experimental Study and Numerical Simulation of Leaking Process of Sand and Water in Underground Engineering[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(12): 2458-2471. |


