2. 吉林大学地球探测科学与技术学院, 长春 130026
2. College of GeoExploration Science and Technology, Jilin University, Changchun 130026, China
0 引言
物探长剖面测量依靠GPS (global positioning system)技术、惯性导航技术及数据处理技术[1],主要应用于陆地地形高度测量系统和水域深度测量系统。物探长剖面测量为重磁测量确定准确的三维坐标,进而进行区域地质构造研究[2],应用于高铁、高速公路等的工程建设。由于长距离线路跨度较大,通常将工程分成多个高斯投影带,而采用高斯投影方法会导致投影长度变形过大,因此需要采用相应措施将这种变形控制在工程允许范围之内。国内外针对长距离物探剖面测量投影长度变形控制方法研究的文献很少,大部分相关文献只借助椭球膨胀法、椭球平移法及椭球变形法用来解决高程归化的改正[3-6],并未有效解决高斯分带投影的误差[7]。斜轴变形椭球高斯投影方法不仅可以有效减少高斯投影横坐标变形误差,还可以减小因高程引起的投影变形[8]。因此,斜轴变形椭球高斯投影方法应用于东西跨度较大的物探长剖面测量能够得到精度较高的结果。
本文研究剖面为漠河—呼和浩特物探长剖面,北东—南西走向,地形起伏较大,横跨高斯投影6°带的19—21带,路线长度约2 300 km。2015年7—8月,笔者利用高精度GPS进行快速静态测量,通过采用斜轴高斯投影,并进行GPS数据处理,获得长剖面测线的测点大地坐标。本文基于斜轴变形椭球,选择斜轴变形椭球高斯投影方法,使斜轴高斯投影的中央经线与物探长剖面走向一致,将测区内测点位于斜轴变形椭球的中央子午线附近,以避免高斯分带与投影综合变形引起的误差,以期为物探长剖面测量的测点采集和数据处理精度的提高发挥作用。
1 斜轴变形椭球投影原理为了有效控制投影长度的变形,减少线路上各控制点距高斯投影中央子午线的距离,使其中央子午线沿线路延伸方向各点横向坐标y值减小,需要构建斜轴变形椭球。构建斜轴变形椭球,需要对地球参考椭球E0(即基础椭球)进行旋转、变形。构建过程如下:
1) 由基础椭球E0上测点的大地坐标(B,L,H)求出E0的参心空间直角坐标系坐标(x,y,z)。
2) 借助旋转矩阵A建立一个新的斜轴椭球记为E1,并求得E1的参心空间直角坐标系(x1, y1, z1)。
3) 求出测点在E1椭球上的大地坐标(B1, L1, H1)。
4) 进行椭球变形,得到斜轴变形椭球,记为E2,得到测点在E2椭球上的大地坐标(B2, L2, H2)。
5) 基于斜轴变形椭球E2实现高斯投影及变形分析。
1.1 斜轴椭球E1的转换模型及基础参数将基础椭球E0上各测点的大地坐标分别转换为空间直角坐标,设定指向0°子午线与赤道交点C的方向为x轴,指向北极N的方向为z轴,由此建立右手参心空间直角坐标系O-xyz(图 1)。则在基础椭球E0上的任意测点P的参心空间直角坐标P(x,y,z)可表示为
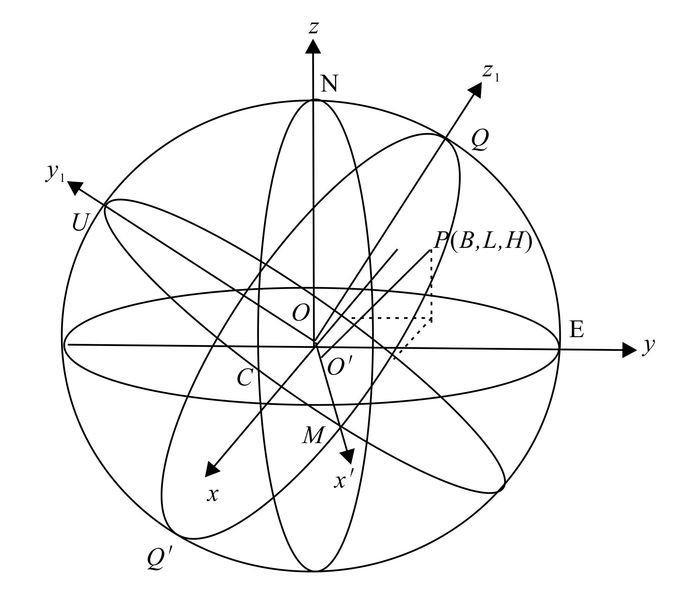
|
| 图 1 基础椭球E0坐标及建立斜轴椭球E1示意图 Figure 1 Basic ellipsoid E0 coordinates and the establishment of an inclined axis ellipsoid E1 schematic diagram |
|
|
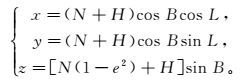 (1)
(1) 式中:(B,L,H)表示测点P在基础椭球E0上的大地坐标;e为E0基础椭球的第一偏心率;N为对应大地纬度B的卯酉圈曲率半径,其公式表示为
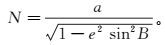 (2)
(2) 式中,a为地球长轴半径。
根据所有测点线路在基础椭球E0上的分布,设定某一靠近于这条线路的剖面椭圆QMQ′的法向量为α=[m n 1],则可建立剖面椭圆QMQ′所在平面的方程:mx+ny+z=0。以剖面椭圆QMQ′作为新椭球的中央子午线, 其中点Q为E1的极点,M为剖面QMQ′与赤道的交点,OM为E1的长半轴,OQ为其短半轴。以短半轴OQ为旋转轴将截面椭圆进行旋转,建立以OQ为z1轴,OM为x1轴的斜轴椭球E1。为了将斜轴椭球E1的中央子午线接近于尽可能多的点,以满足高斯投影平面坐标中y坐标较小的要求,设J为每个测点点集Pi(xi,yi,zi)的x、y坐标矩阵,W为对应的z坐标列向量,已知W和J矩阵的关系式[8]为
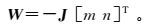 (3)
(3) 式中,m、n为需要解得的系数。通过最小二乘法可得
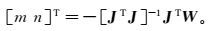 (4)
(4) 由基础椭球E0的x、y、z轴指向的OC、OE、ON方向的3个单位向量旋转至斜轴椭球E1的x1、y1、z1轴指向的OM、OU、OQ方向,需要借助旋转矩阵A。若x1轴的指向为所测测点方向的正方向,则计算所得的测点在斜轴椭球E1上的相对经差会很小,可直接使用其正向转换模型:
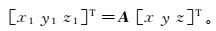 (5)
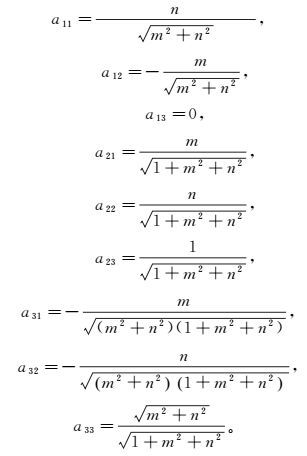
(5) 式中,旋转矩阵A为
 (6)
(6) 
若x1轴指向测区相反方向,则所求得的测点经差绝对值接近于π,不利于计算,需要将斜轴椭球E1绕着z1轴旋转180°,则正向转换模型为
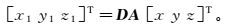 (7)
(7) 式中,D为对角矩阵,D=diag[-1-1 1]。
因为斜轴椭球E1的参数与剖面QMQ′在基础椭球E0上的大地纬度B0有关[9],最终斜轴椭球E1的基本参数短半轴b1、第一及第二偏心率平方可简化为关于m、n的表达式:
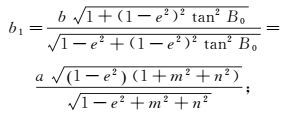 (8)
(8)  (9)
(9) 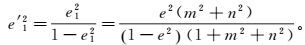 (10)
(10) 通过测区内测点在斜轴椭球E1的空间参心直角坐标及斜轴椭球的基本参数,根据改进的最佳算法[10-11],可以借助中间变量u推导出测点在斜轴椭球E1的大地坐标B1、L1、H1:
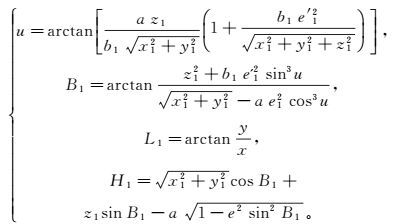 (11)
(11) 如果测点在斜轴椭球E1上的大地高过大,在直接进行高斯投影时变形较大。根据椭球变换理论,不仅可以降低投影横坐标,还能尽可能地减小大地高。椭球变形法不会引起大地经度的变化,但对大地纬度和大地高均有影响,同时改变椭球的长半径和扁率,对应改变量与基准点所在位置及大地高变化量有关[4],即
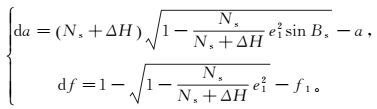 (12)
(12) 式中:da为斜轴椭球E1到斜轴变形椭球E2的长半径的改变量;df为扁率改变量;ΔH为基准点处的大地高改变量;Bs为基准点在E1上的纬度;Ns为基准点处的卯酉圈曲率半径;f1为E1的扁率。已知空间直角坐标解算B1的精度为10-7,根据函数误差方法,da的精度为10-14,df的精度为10-21。由椭球变形法性质可知斜轴变形椭球E2上的大地坐标[12]:
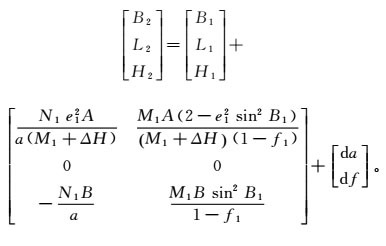 (13)
(13) 式中:A=sin B1cos B1;B=1-e12sin2B1;M1、N1分别为斜轴椭球E1的子午圈曲率半径和卯酉圈曲率半径。
2 斜轴变形椭球高斯投影“斜轴变形椭球高斯投影方法”以斜轴变形椭球E2为投影椭球,并以该椭球的中央子午线为基准进行与高斯投影一致的投影,属于等角横切椭圆柱投影。进行投影时,椭球参数采用新椭球E2的几何参数,实现斜轴变形椭球E2上大地坐标到平面坐标的转换。计算公式为[13]
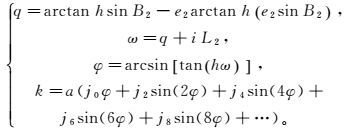 (14)
(14) 式中:q为测点在斜轴变形椭球E2上的等量纬度;x为纵坐标,y为横坐标,则k=x+iy为对应的高斯投影平面复数坐标;系数i、h、j0、j2、j4、j6、j8、…的设置参考文献[13]。
在高斯投影中,长度变形主要由两部分构成:一是将测区表面归算至参考椭球面的高程归化长度变形;二是将参考椭球面投影至高斯平面上产生的投影长度变形。
高程改正是通过将地面上观测到的长度归化到参考椭球面上而产生的变形:
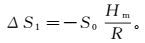 (15)
(15) 式中:ΔS1是高程改正;S0是地面观测长度;Hm是地面两点高出参考椭球面的平均高度;R是归算边方向参考椭球法截弧的曲率半径(取值6 378 km)。
投影改正是将参考椭球面上的长度投影到高斯面上而产生的变形:
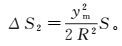 (16)
(16) 式中:ym是高斯平面上边长两端点横坐标的平均值;S为参考椭球面长度。
长度综合变形则为高斯投影平面上的长度与地面长度之差,约等于高程归化长度变形与投影长度变形之和[13]:
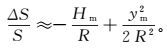 (17)
(17) 根据地球物理工作需要,本次长剖面测量为北东—南西走向,北起漠河北极村,南至呼和浩特市区边缘,途经满归、根河、海拉尔、阿尔山、东乌珠穆沁旗、锡林浩特、苏尼特左旗和四子王旗,地形起伏较大,横跨高斯投影6°带的19—21带,总路线长度约2 300 km,利用高精度GPS进行快速静态测量,边长1 km左右。同时利用CG5重力仪采集测点的重力数据,在每段测区中间架设日变站,利用磁力仪采集各测点磁场大小周期变化。利用TBC (trimble business center)数据处理软件进行GPS数据处理,获得长剖面测线共2 158个测点的大地坐标(图 2)。
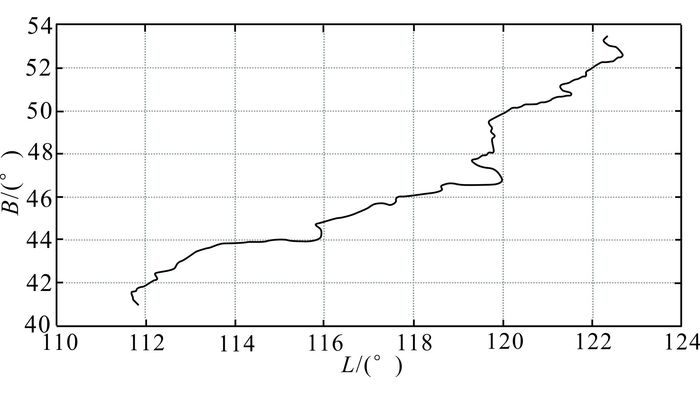
|
| 图 2 测区内测点分布图 Figure 2 Test area measuring points distribution map |
|
|
根据测区内总共2 158个测点的线性拟合,得到直线方程B2=-23.890 577 L2-0.261 245 4。将拟合的直线作为测线的中央经线,测点分布于斜轴变形椭球的中央子午线附近,有效减小测点的高斯投影横坐标变形。
3.3 长剖面投影及变形分析由于测区跨度较大,根据普通高斯-克吕格投影分带的方法将测区分为3带。分别计算每个测点距所在投影带中央子午线的距离,得到距离中央子午线距离最大的点高斯投影综合变形最大值为6 023.794 6 mm/km,投影综合变形较大,所以此方法不适用于长剖面的高精度重力测量要求。
按照斜轴变形椭球高斯投影方法,可算出:
m=2.279 627 066 445 72,
n=-0.012 372 623 424 154 00;
E0到E1参心直角坐标系的旋转矩阵为

则可以得到斜轴椭球E1的短半轴为
b1=6 360 188.657 683 58,
第一偏心率平方为
e12=0.005 620 164 203 499 64,
第二偏心率平方为
e′12=0.005 651 928 972 390 99,
以及测点在E1的直角坐标系,进而求得测点的大地坐标系。
选定基准点处的纬度Bs=53.444 073 19°,令ΔH=368.962 m,Ns=6 391 957.171,将斜轴椭球进行变形,得到斜轴变形椭球E2的第一偏心率平方e22=0.005 620 002 004 694 17及测点在E2上的大地坐标。
经过计算,测区内大地高最大值为1 432.105 m,最小值为227.936 m,测区最左端相对于斜轴变形椭球E2的经差为-3′16.806″,最右端相对于斜轴变形椭球E2的经差为-8.590″。高程归化长度变形的中误差绝对值为53.039 mm/km,高斯投影长度变形中误差为67.87 mm/km,投影综合变形的中误差为88.51 mm/km。
通过对高斯投影和斜轴变形椭球高斯投影两种方法计算得出相应测点的投影综合变形进行对比(图 3)可知:高斯投影测点经度跨度较大,该方法计算出的综合投影变形数据整体变形较大,由于距离中央经线近的变形小,在中央经线上没有长度变形,而变形随着距中央经线距离的增大而变大,同时地形起伏对投影变形具有一定的影响;而利用斜轴变形椭球计算出来的数据则保持在一个合理的数据要求范围内,达到比较理想的结果。在此情况下,考虑斜轴投影能较好地解决分带及边缘误差较大的问题。
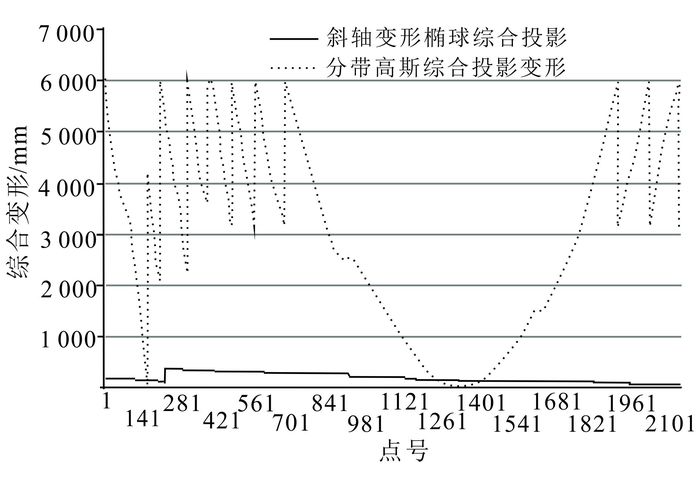
|
| 图 3 投影变形对比 Figure 3 Projection deformation contrast diagram |
|
|
选取斜轴变形椭球高斯投影的方法,利用最小二乘法、坐标系旋转法和椭球变换法等理论构建斜轴变形椭球,应用于东西跨度较大的线路中测点的投影。斜轴变形椭球高斯投影变形方法可以有效减少高斯投影横坐标及因高程引起的投影变形,避免由于东西跨度较大而出现的高斯投影分带变形问题。结合地球物理重力测量和磁法测量工作,利用GPS快速静态测量方法,获得工作区中测点的实际数据并进行了验证,得到了较好的结果。研究结果表明,斜轴变形椭球高斯投影方法应用于东西方向长距离剖面测量会提高投影精度,为物探方法提供精确的平面和高程位置。
| [1] |
任秀云, 刘立宝, 杨君国, 等. 机载脉冲激光雷达剖面测量技术的进展及应用[J].
遥感技术与应用, 2011, 26(3): 392-398.
Ren Xiuyun, Liu Libao, Yang Junguo, et al. Development and Applications of Airborne LiDAR Profilometer[J]. Remote Sensing Technology and Application, 2011, 26(3): 392-398. DOI:10.11873/j.issn.1004-0323.2011.3.392 |
| [2] |
刘财, 杨宝俊, 冯晅, 等. 论油气资源的多元勘探[J].
吉林大学学报(地球科学版), 2016, 46(4): 1208-1220.
Liu Cai, Yang Baojun, Feng Xuan, et al. Multivariate Exploration Technology of Hydrocarbon Resources[J]. Journal of Jilin University (Earth Science Edition), 2016, 46(4): 1208-1220. |
| [3] |
李世安, 刘经南, 施闯. 应用GPS建立区域独立坐标系中椭球变换的研究[J].
武汉大学学报(信息科学版), 2005, 30(10): 888-891.
Li Shi'an, Liu Jingnan, Shi Chuang. Study of the Ellipsoid Transformation on the Establishment of Local Independence Coordinate System Using GPS Technique[J]. Geomatics and Information Science of Wuhan University, 2005, 30(10): 888-891. |
| [4] |
况金著, 夏神州. 通过椭球变换建立区域坐标系的高斯投影算法[J].
地矿测绘, 2011, 27(4): 11-14.
Kuang Jinzhu, Xia Shenzhou. Establish Regional Coordinate System with Gauss-Kruger Projection Calculation Through Ellipsoid Transformation[J]. Surveying and Mapping of Geology and Mineral Resources, 2011, 27(4): 11-14. |
| [5] |
吕慧玲. 斜轴墨卡托投影方法在郑西客专中的应用研究[J].
测绘信息与工程, 2009, 34(1): 26-28.
Lü Huiling. Application of Oblique Mercator Projection Method to Zhengxi Special Passenger Transport Line[J]. Journal of Geomatics, 2009, 34(1): 26-28. |
| [6] |
王解先, 伍吉仓, 高小兵. 斜轴墨卡托投影及其在高铁建设工程中的应用[J].
工程勘察, 2011, 39(8): 69-72.
Wang Jiexian, Wu Jicang, Gao Xiaobing. Oblique Mercator Projection and Its Applications on High Speed Railway Construction[J]. Geotechnical Investigation & Surveying, 2011, 39(8): 69-72. |
| [7] |
杨启和. 论高斯投影换带的数值计算方法[J].
测绘学报, 1982, 11(1): 18-31.
Yang Qihe. Discussing the Numerical Method of Gauss Projection Changer[J]. Acta Geodaetica et Cartographica Sinica, 1982, 11(1): 18-31. |
| [8] |
边少锋, 刘强, 李忠美, 等. 斜轴变形椭球高斯投影方法[J].
测绘学报, 2015, 44(10): 1071-1077.
Bian Shaofeng, Liu Qiang, Li Zhongmei, et al. An Alteration of Gauss Projection Based on Oblique Deformed Ellipsoid[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(10): 1071-1077. |
| [9] |
曾启雄. 空间直角坐标直接解算大地坐标的闭合公式[J].
测绘学报, 1981, 10(2): 83-95.
Zeng Qixiong. Solve Geodetic Coordinates Closed Equation with Space Cartesian Coordinate[J]. Acta Geodaetica et Cartographica Sinica, 1981, 10(2): 83-95. |
| [10] |
边少锋, 柴洪洲, 金际航.
大地坐标系与大地基准[M]. 北京: 国防工业出版社, 2005.
Bian Shaofeng, Chai Hongzhou, Jin Jihang. Geodetic Coordinates and Geodetic Datum[M]. Beijing: National Defense Industry Press, 2005. |
| [11] | Bowring B R. The Accuracy of Geodetic Latitude and Height Equations[J]. Survey Review, 1985, 28(218): 202-206. DOI:10.1179/sre.1985.28.218.202 |
| [12] |
赵长胜. 高斯投影坐标反算的迭代算法[J].
测绘通报, 2004(3): 16-17.
Zhao Changsheng. Iterative Algorithm of Gauss Projection Plane Rectangular Coordinates[J]. Bulletin of Surveying and Mapping, 2004(3): 16-17. |
| [13] |
李厚朴, 边少锋. 高斯投影的复变函数表示[J].
测绘学报, 2008, 37(1): 5-9.
Li Houpu, Bian Shaofeng. The Expressions of Gauss Projection by Complex Numbers[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(1): 5-9. |



