2. 中国地震局地球物理研究所, 北京 100081;
3. 上海市地震局, 上海 200062
2. Institute of Geophysics, CEA, Beijing 100081, China;
3. Earthquake Administration of Shanghai Province, Shanghai 200062, China
0 引言
地震波走时速度研究是地球物理学基础研究,包括基础的水平分层速度研究,以及倾斜分层速度研究、三维速度模型研究、S波分裂研究等等。研究方法包括了体波、面波、接收函数和有限频方法等。体波研究方法是经典方法,包括古登堡方法(又称拐点法)和Herglotz-Wiechert法(又称积分法)。前者利用走时曲线的拐点来获得对应走时速度,只能计算700 km以上的速度分布,且对走时曲线的精确性有要求;后者利用阿贝尔积分方程对时距公式进行求解,需要对震源深度以上的介质进行“剥壳”处理。依据这些经典方法,1975年Dziewonski等[1]在对大量地震波走时数据分析的基础上,提出了标准参考地球模型(PREM)。面波方法主要研究地壳和上地幔结构,主要包括两类:一是频散反演方法,二是面波波形反演方法。前者假设面波沿大圆路径传播,绘制相速度和群速度频散曲线,得到各网格的纯路径频散曲线,然后反演地震波三维速度结构。后者用基阶和高阶面波波形拟合反演三维速度结构,利用波形记录的丰富信息,对地壳和上地幔的精细结构进行研究。面波方法一般用于区域模型研究,朱介寿等[2]使用面波频散和波形拟合反演方法,对东亚及西太平洋边缘海地区的地壳和上地幔进行了高分辨率三维S波速度成像。Pan等[3]利用西准噶尔盆地70 km测线得到的400条频散曲线,给出了1.5 km深度、60 km长的二维剪切波成像。Mohanty等[4]对西藏和印度地区的P波速度结构和各向异性进行了研究。薛林福等[5]在大量实践基础上提出了分块三维地质建模方法,以断裂和岩体边界为边界,将研究区分解为内部构造相对简单的地质单元,分别对每一单元进行地质和地球物理研究,揭示深部地质结构,基于剖面建模构建整个区域的三维地质模型。曾融生[6]对大陆地区的莫霍面深度进行了研究,绘制了大陆及邻区的莫霍面深度图。Watts[7]对全球岩石圈的一维速度模型进行了研究。另外,速度模型研究与地震定位研究[8-19]有密切的联系,二者存在耦合关系,定位研究的进展常常会推动速度模型研究的进展。
山东省境内中部山地突起,西南、西北低洼平坦,东部缓丘起伏,形成以山地丘陵为骨架、平原盆地交错环列其间的地形大势。海拔最高点为中部泰山,主峰海拔1 532 m,最低点为黄河三角洲,海拔10 m。山东省地层发育比较齐全,从老到新有太古宇泰山群;元古宇—太古宇胶东群,胶南群;元古宇粉子山群,蓬莱群,济宁群及土门组;古生界寒武系,奥陶系(中、下统),石炭系(中、上统),二叠系;中生界侏罗系,白垩系;新生界第三系,第四系。缺失志留系、泥盆系、奥陶系上统、石炭系下统、三叠系等地层。基岩出露面积约占全省面积的五分之三。
地层的分布特征基本上可分为三区。以沂沐断裂带的昌邑—大店深大断裂为界,全省地层分成东西两部分,地层发育情况有很大差别。东部(鲁东地区)发育元古宇—太古宇胶东群,元古宇粉子山群、蓬莱群及中生界,新生界不甚发育;西部鲁中南地区除胶东群、胶南群、粉子山群、蓬莱群外,其余地层发育较全,鲁西、北地区则发育很厚的新生界。山东历史上发生过8.5级强震,以及若干次6~7级地震。郯庐断裂带纵贯南北,具备发生强震的地质构造条件。对于本地区的详细地球物理背景研究是具有现实意义的。林怀存[20]给出了山东省近震地震波速和地壳结构的结果,显示山东省上地壳的波速为6.18 km/s,地壳厚度为36 km,中西部较厚而东部较薄。李铂等[21]根据VELEST方法给出了山东省的一维速度结构研究结果。黄建平等[22]利用重力和地形观测反演了中国及临区地壳厚度。孙耀庭等[23]、王淑萍等[24]、代杰瑞等[25]、黄超等[26]对山东地区的矿区、地层和断裂进行了地球化学和地质学研究,这些研究揭示了研究区内部子区域的地学背景。邱毅等[27]、王晓娜等[28]对福建和龙门山地区的一维速度模型进行了研究。当前山东省地震定位和编目均使用华南速度模型,该模型由范玉兰等[29]根据福建及其周边的地震资料给出,由于未使用本区域数据资料,对本区域研究和具体工作适用性存在一定差异。现在根据我省数字地震台网近十年丰富的地震数据资料,本文进行了本区域的地震波速度模型研究。
1 理论本文通过单层地壳模型说明初始模型的建立方法。单层模型的地震波速度为
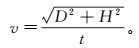 (1)
(1) 式中:v为该层地震波的速度;D为震中距;H为震源深度;t为对应走时。在D>>H的情况下,式(1) 可以化简为
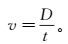
本文对走时曲线的数据点进行拟合,所得曲线的斜率倒数即为该层地震波波速。另外,本文使用了Hyposat对地震事件进行批量重定位,根据重定位的评价残差来评估模型的优劣。Hyposat为Geiger定位方法的改进,即求解以下目标函数极小值:

式中:(t0, x0, y0, z0)为地震的震源发震时刻及发震震中;ri为第i个台站的对应残差,即理论到时与实际到时之差;n为台站数量。Hyposat方法的改进之处包括:使用了射线参数或者视速度反演,该参数的残差可以较好地评估震相质量;使用了更丰富的震相信息,包括pP (P波的两次反射波,其中离开震源的射线方向偏向地表)、sP (反射波,离开震源射线方向偏向地表,为S波,在地表反射后转换为P波)等;反演过程使用了奇异值分解(singular value decomposition,SVD)方法,提高了计算速度和稳定度。
本文的研究对象为山东地区的一维地震波走时速度模型。基于上下地壳的地质学背景,该模型分为三层,分别对应上地壳、下地壳和地幔,目标参数包括对应层的深度(上地壳深度h1, 下地壳深度h2)、P波速度(vP1、vP2、vP3)和S波速度(vS1、vS2、vS3)。研究步骤主要分为4步:
第一步,计算P波和每层厚度的初始模型。使用的方法是走时曲线拟合,拟合曲线的斜率倒数即为对应参数。
第二步,使用Hyposat批量重定位方法,确定P波和每层厚度的最优模型。在初始模型的基础上,加入扰动生成大量速度模型。将每个速度模型用大量地震事件的批量重定位,根据最终的残差来确定最优模型。
第三步,S波参数的计算,在最优模型基础上,对S波加入扰动,对所有扰动模型进行批量重定位,根据残差确定最优模型。
最后一步为模型的检验,通过多种方法将最优模型与原始模型进行对比,确定最终模型。
2 数据本文使用的数据主要包括三部分,分别是:1) 2009—2016年M≥0.1(M为震级)的1 554次地震事件及其走时数据,利用这些数据,通过走时曲线拟合以及相关分析,得到初始模型以及变化范围;2) 10个较大地震的波形数据,用于标定Pb (P波在康拉德面的首波)震相,给出相应的速度参数;3) 55个地震事件走时数据,包括多于7条的Pn (P波在莫霍面的首波)震相,本文使用这部分数据进行批量地震重定位,并基于重定位结果给出最终模型。
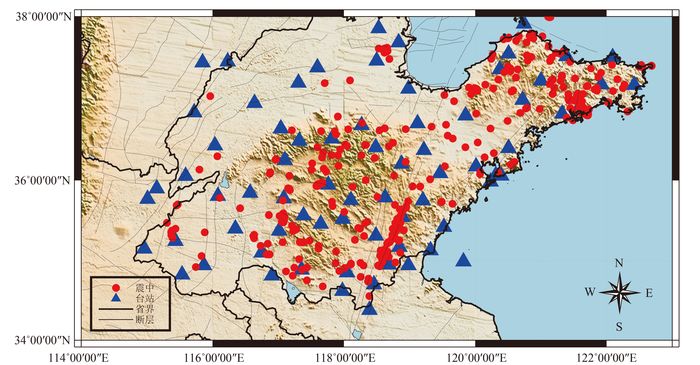
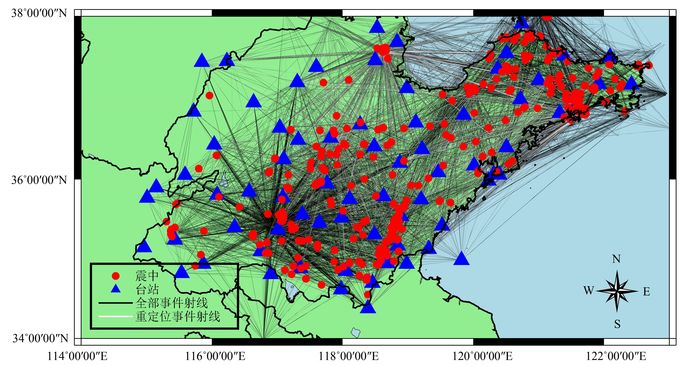
为了提升数据的使用效果,本文使用以下方法去除数据的异常点,具体方法为:以Pg (P波的直达波)震相数据为例,将所有走时数据的走时和震中距进行散点投影,并对该散点集合进行直线拟合,根据每个点到拟合直线的距离进行判定,如果距离超过指定阀值,则认为该点为异常点数据,删除该点数据。将全部异常点删除后,剩下的数据重新进行拟合,可以认为该数据的拟合效果要好于原始数据。图 1为震中分布图,图 2为射线分布图。
|
| 图 1 震中和台站分布图 Figure 1 Epicenter and station map |
|
|
|
| 图 2 地震射线分布图 Figure 2 Seismic ray map |
|
|
从图 1和图 2可以发现,本文所用的地震事件和地震射线较为均匀地覆盖了目标研究区域,不存在明显的空区。
3 模型 3.1 P波和层厚度初始模型本文通过走时曲线以及前人的工作给出地震波速度模型的初始模型,以及大概的变化范围。具体做法如下:
1) 用走时曲线拟合给出地壳上层波速vP1、vS1和地幔顶部波速vP3、vS3;
2) 对10个典型地震重新标志震相,主要是给出Pb震相,然后利用这些震相数据获得地壳下层波速vP2、vS2;
3) 结合前人工作,可以获得康拉德面参考值H1和地壳厚度参考值H2,将以上参数以及震相数据绘制折合走时曲线图,给出参考的初始模型以及模型的变化范围。
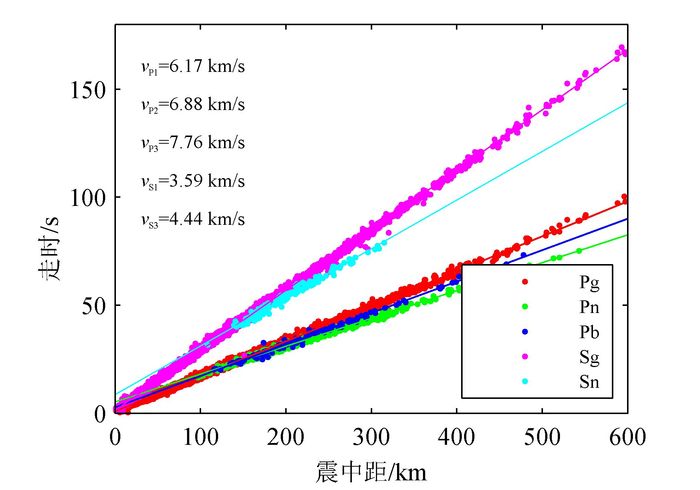
图 3为各类震相的走时曲线图。Pb走时点数据来自10个典型地震的重新标志震相。通过计算,得到初始速度模型为:vP1=6.17 km/s,vP2=6.88 km/s,vP3=7.76 km/s。
|
| Sg. S波的直达波;Sn. S波的首波。 图 3 走时曲线图 Figure 3 Travel time curve figure |
|
|
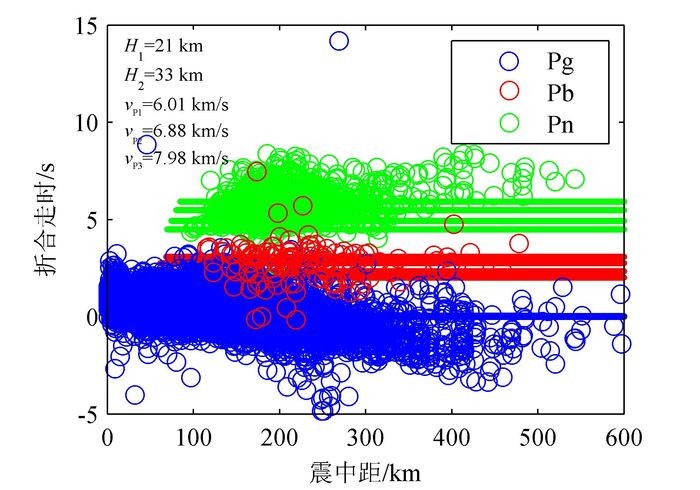
本文参考曾融生[6]以及Crust1.0[7]的地壳厚度结果,认为山东地区地壳厚度约为33 km。将以上参数和走时点作为基础数据,绘制折合走时曲线图,如图 4所示。需要说明,图 4中4条绿色曲线分别代表不同震源深度的理论折合曲线,曲线上数字即为对应的震源深度,红色曲线和蓝色曲线同理。通过不断变换图 4的参数,可以使得折合走时曲线与走时点的符合程度趋于良好,并给出模型参数的变化范围。最终的模型变化范围如表 1所示。
|
| 图 4 折合走时曲线图 Figure 4 Reduced travel time curve figure |
|
|
| vP1/(km/s) | vP2/(km/s) | vP3/(km/s) | H1/km | H2/km | |
| 下限 | 6.0 | 6.8 | 7.7 | 20.0 | 30.0 |
| 上限 | 6.2 | 6.9 | 8.0 | 23.0 | 36.0 |
在获得了初始模型变化范围后,本文可以利用Hyposat软件对55个典型地震进行批量重定位。通过逐步缩小模型参数的步长,可以获得一批较为准确的优质模型组合,这些模型的定位残差均较小,且均在给定的模型变化范围以内。批量重定位的55个地震事件的挑选依据是Pn震相的数量。由于Pn震相可以约束地壳厚度和下地壳、地幔顶部的速度结构,且可以较好地约束地震震中的深度,因此本文根据Pn震相数量进行地震事件数据的选择,最终筛选了55个地震事件。具体做法分为两步。第一步步长较大,采用表 1的参数作为上下限,步长设为0.10 km/s和1.0 km。第一步可以给出一个残差最小的结果,第二步在该结果基础上进行小范围扰动,并缩小步长为0.10 km/s和0.5 km,然后分析残差最小的模型,如表 2所示。
| vP1/(km/s) | vP2/(km/s) | vP3/(km/s) | H1/km | H2/km | RMS/s |
| 6.13 | 6.88 | 7.93 | 22.0 | 34.0 | 0.353 |
| 6.13 | 6.88 | 7.93 | 23.0 | 33.5 | 0.354 |
| 6.13 | 6.88 | 7.93 | 23.0 | 34.0 | 0.355 |
| 6.13 | 6.88 | 7.93 | 20.0 | 34.0 | 0.357 |
| 6.13 | 6.88 | 7.93 | 21.0 | 34.0 | 0.359 |
| 6.13 | 6.88 | 7.93 | 22.0 | 33.0 | 0.360 |
| 6.13 | 6.88 | 7.93 | 20.5 | 34.0 | 0.360 |
| 注:RMS为定位结果的残差。 | |||||
结合本文之前的该地区背景调查,以及物理上的考虑,本文认为最好的模型如表 3所示。
| vP1/(km/s) | vP2/(km/s) | vP3/(km/s) | H1/km | H2/km | RMS/s |
| 6.13 | 6.88 | 7.93 | 22.0 | 33.0 | 0.360 |
需要说明的是,这个模型并不是残差最小的模型,而是考虑了地区区域实际物理背景而进行的人工挑选,而且还要经过后面的模型检验,如果模型检验结果不佳,还要进行重新挑选。
3.3 S波速度模型在得到P波的速度结构之后,本文继续探索S波的速度结构。S波与P波的速度有一定联系,在地震学理论中,对于理想泊松体,其P波和S波的波速比值约为1.73;考虑到地球物理实际情况,深层介质波速比常常高于浅层。据此,具体做法如下。1) 搜索最优波速比:P波速度不变,变动波速比为1.70~1.75,从1.70开始,以0.01的步长增至1.75,得到6组不同的S波波速;然后对6组速度结构进行批量地震事件重定位,根据评价残差极小值得到最优波速比。据此,本文得到的最优波速比为1.72。2) 对vS1使用最优波速比,vS2和vS3分别迭代循环所有的波速比,且使得从上层到下层的波速比为递增。计算所有速度模型的定位结果,根据定位结果平均残存极小值确定最优速度模型,如表 4所示。
| vP/(km/s) | vS/(km/s) | H/km | |
| 上地壳 | 6.13 | 3.564 | 22 |
| 下地壳 | 6.88 | 3.909 | 33 |
| 地幔顶部 | 7.93 | 4.455 | |
| 注:H为地层下界面的深度。 | |||
在获得了最优模型后,本文利用多种方法对模型进行检验。
3.4.1 典型事件检验本文通过选择典型的天然地震和非天然地震事件,用原始模型和最优模型进行重定位,然后比较两种定位结果的残差优劣等。非天然地震事件定位过程中要锁定震中深度为0。最终的地震定位结果如表 5、6所示。
| 模型 | 日期 | 时刻 | 经度/(°) | 纬度/(°) | 深度/km | RMS/s | 定位方法 | 震相数据 |
| 编目 | 20120906 | 0:41:06 | 117.058 | 34.802 | 7 | 0.400 | 单纯型 | 观测报告 |
| 原始模型 | 20120906 | 0:41:06 | 117.077 | 34.816 | 9 | 0.408 | Hyposat | 重标震相 |
| 最优模型 | 20120906 | 0:41:07 | 117.071 | 34.803 | 9 | 0.349 | Hyposat | 重标震相 |
| 模型 | 日期 | 时刻 | 经度/(°) | 纬度/(°) | 深度/km | RMS/s | 定位方法 | 震相数据 |
| 编目 | 20150502 | 5:51:02 | 116.902 | 35.393 | 0 | 0.300 | 单纯型 | 观测报告 |
| 原始模型 | 20150502 | 5:51:02 | 116.917 | 36.393 | 0 | 0.229 | Hyposat | 重标震相 |
| 最优模型 | 20150502 | 5:51:02 | 116.908 | 36.390 | 0 | 0.168 | Hyposat | 重标震相 |
通过表 5、6可以发现,最优模型比原始模型获得了较低的残差,且位置与编目位置更为接近,显示最优模型比原始模型在定位上效果更好。
3.4.2 定位结果比较与讨论本文将原始模型和最优模型的定位结果与地震目录进行对比,定位的事件为55次批量重定位事件,定位的具体方法和速度结构等见表 7。
| 定位方法 | 速度结构 | 走时数据 | |
| 目录定位结果 | 单纯型 | 华南模型 | 观测报告数据 |
| 原始模型结果 | Hyposat | 华南模型 | 观测报告数据 |
| 最优模型结果 | Hyposat | 最优模型 | 观测报告数据 |
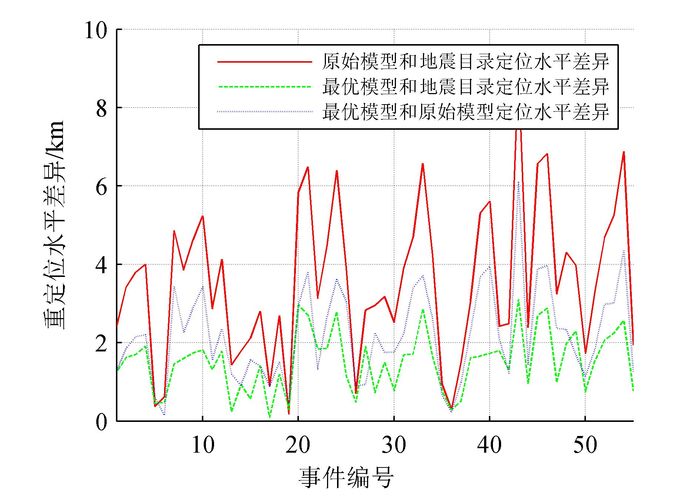
这些定位结果的震中差异一般在3 km左右,这种差异在大区域震中分布图上难以观察,因此本文将这3种定位结果的水平震中差异描绘成曲线图,可以更好地观察其定位效果,如图 5所示。从图 5可以看出,原始模型、最优模型和地震目录3种定位结果的起伏是较为一致的,这种情况可能与地震事件的台站布局和数据质量有关。
|
| 图 5 3种定位水平差异比较图 Figure 5 Comparation ofthree epicenter difference |
|
|
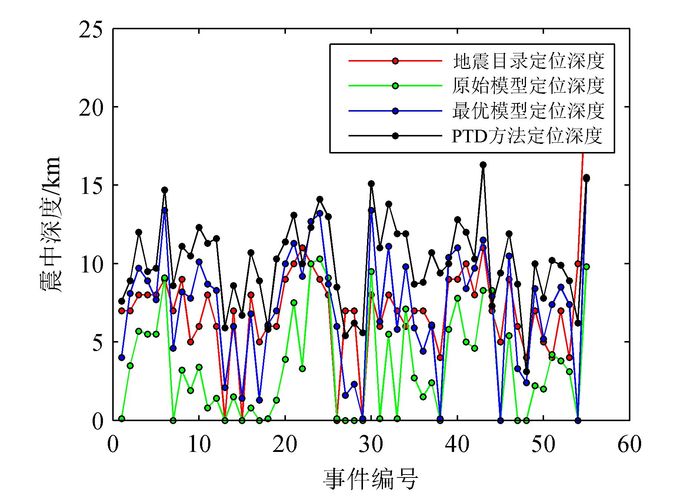
朱元清等[16]给出了测定地震震源深度的PTD (P wave time difference)方法,该方法利用首波和直达波的相对关系进行地震震源深度的测定,在地震震源深度测定方面精度较高。图 6为原始模型、最优模型、地震目录和PTD方法4种定位结果的深度显示,具体的震相和定位方法等见表 8。
|
| 图 6 4种定位结果深度比较图 Figure 6 Comparation offour epicenter depth |
|
|
| 定位方法 | 速度结构 | 震相数据 | |
| 地震目录定位深度 | 单纯型 | 华南模型 | 观测报告数据 |
| 原始模型定位深度 | Hyposat | 华南模型 | 观测报告数据 |
| 最优模型定位深度 | Hyposat | 最优模型 | 观测报告数据 |
| PTD方法定位深度 | PTD | 最优模型 | 观测报告数据 |
从图 6可以看出,原始模型定位效果较差,相当部分点位于地表或者接近地表,这说明原始模型不太适合当前研究区;PTD定位结果较为合理,均匀散布于5~15 km范围内,这一方面说明了其深度定位方法的合理性,也暗含了最优速度模型的优越性;地震目录定位结果普遍集中于7~9 km范围,出现地表地震情况较少,但是其深度过于集中于小区域,结果也不尽合理;最优模型定位深度变化范围也较大,也反映了最优模型的合理性。
另外,通过图 5分析Hyposat和单纯型的定位效果可以发现,最优模型与地震目录定位的差异最小,即目录结果的定位效果优良。而地震目录为原始模型和单纯型方法的结果,所以在速度模型较差(即原始速度模型)的情况下,单纯型定位效果仍然较优,同样,原始模型与地震目录定位差异最大,即相对目录结果,原始模型的Hyposat方法定位效果不好。分析其原因,这种现象可能源于算法的原理。单纯型方法为非线性算法,按照一定规则进行全局搜索,对于全局的大部分区域都有涉及,特点是计算速度慢,不会陷入局部极小。Hyposat则是线性迭代算法,按照梯度向最优的方向进行迭代计算,计算速度快,但容易陷入局部极小。这可能是以上现象的内部原因:即Hyposat作为线性算法,在速度模型较好时可以迅速得到较优的结果,但速度模型较差时,则容易陷入局部极小,结果偏离较大。而单纯型方法则相反,速度模型较差时,由于全局搜索的特性,不容易陷入局部极小,仍可得到较优的结果。
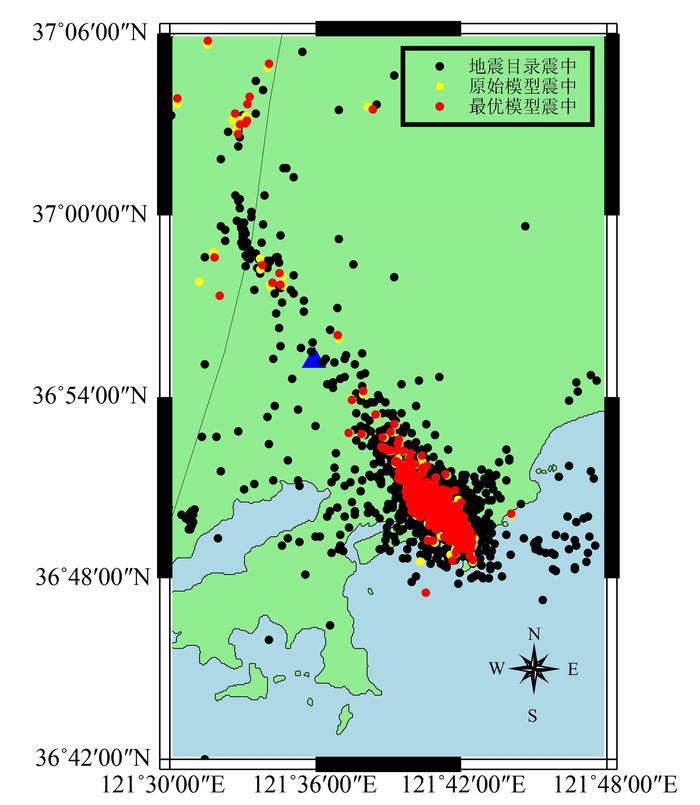
3.4.3 乳山、长岛震群双差定位研究本文使用双差定位方法对乳山和长岛震群进行定位,速度模型分别为原始模型和最优模型,并分析其定位差异。乳山震群为2007—2016年的3 075次地震事件,长岛震群为2008—2016年的400次地震事件。
|
| 图 7 乳山震群震中分布图 Figure 7 Epicenter of Rushan earthquake clusters |
|
|
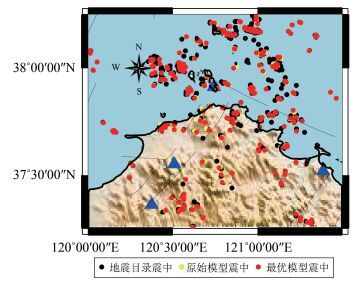
|
| 图 8 长岛震群震中分布图 Figure 8 Epicenter of Changdao earthquake clusters |
|
|
从图 7和图 8可以看出,相对于地震目录震中,原始速度模型的双差定位震中较为收敛,最优速度模型的双差定位震中收敛性最好。这种收敛源于双差定位方法的优异性,其重定位结果一般会使得成簇震群的震中更加汇聚;最优模型定位结果收敛性最明显,则显示了最优速度模型的优异性。
4 结论和讨论1) 山东地区的一维速度模型为vP1=6.13 km/s,vP2=6.88 km/s,vP3=7.93 km/s,H1=22 km,H2=33 km,vS1=3.54 km/s,vS2=3.95 km/s,vS3=4.46 km/s。该模型与走时曲线拟合结果、批量地震重定位结果均较为一致,且经过各种检验,其表现比华南速度模型优良。
2) 通过单纯型方法和Hyposat定位结果的比较,本文发现:单纯型方法即使在较差的速度模型下也可以获得较好的定位结果;而Hyposat的定位效果对速度模型的依赖性较强,即如果速度模型质量不好,则定位结果较差。这主要源于两种方法的原理不同。单纯型方法为非线性方法,其定位思想为全局搜索法,即在整个数据空间寻找满足约束条件极小值的解(此处的约束条件主要是指残差),其计算速度一般不会太快;另外,这类方法不需要计算偏导数矩阵,即使速度模型略差,因为其进行了全局搜索,所以其解仍与最优解差异不大。当然,这里需要说明,如果速度模型与真实模型差异太多,则非线性算法解也会较不理想。Hyposat为基于Geiger法思想的迭代方法,其定位思想为对定位方程进行线性化,利用一阶近似来获得近似解,之后迭代此过程,直至获得最优解;这类定位方法需要计算偏导数矩阵,如果速度模型质量不好,则很有可能导致其定位迭代方向错误,而陷于局部极小的情况。综合以上讨论,本文发现,非线性定位方法对速度模型的依赖性略低,而Geiger类方法则对速度模型依赖性较高。
致谢: 许力生研究员、肖兰喜研究员、宋秀清高级工程师为本文提出了有益的修改意见,刘双庆高级工程师、陈向军高级工程师等为本文提供了部分软件,本文使用Matlab和GMT进行了数据处理和图件绘制,在此致以诚挚的谢意!| [1] | Dziewonski A M, Anderson D L. Preliminary Refe-rence Earth Model[J]. Physics of the Earth & Planetary Interiors, 1981, 25(4): 297-356. |
| [2] |
朱介寿, 曹家敏, 蔡学林, 等. 东亚及西太平洋边缘海高分辨率面波层析成像[J].
地球物理学报, 2002, 45(5): 646-664.
Zhu Jieshou, Cao Jiamin, Cai Xuelin, et al. High Resolution Surface Wave Tomography in East Asia and West Pacific Marginal Seas[J]. Chinese Journal of Geophysics, 2002, 45(5): 646-664. |
| [3] | Pan Y, Xia J, Xu Y, et al. Delineating Shallow S-Wave Velocity Structure Using Multiple Ambient-Noise Surface-Wave Methods:An Example from Western Junggar, China[J]. Bulletin of the Seismological Society of America, 2016, 106(2): 327-336. DOI:10.1785/0120150014 |
| [4] | Mohanty D, Singh A, O'Driscoll J, et al. P Wave Velocity Structure Below India and Tibet Incorporating Anisotropic Delay Time Effects[J]. Geochemistry Geophysics Geosystems, 2016, 17(3): 725-738. DOI:10.1002/2015GC006064 |
| [5] |
薛林福, 李文庆, 张伟, 等. 分块区域三维地质建模方法[J].
吉林大学学报(地球科学版), 2014, 44(6): 2051-2058.
Xue Linfu, Li Wenqing, Zhang Wei, et al. A Method of Block-Divided 3D Geologic Modeling in Regional Scale[J]. Journal of Jilin University(Earth Science Edition), 2014, 44(6): 2051-2058. |
| [6] |
曾融生, 孙为国, 毛桐恩, 等. 中国大陆莫霍界面深度图[J].
地震学报, 1995(3): 322-327.
Zeng Rongsheng, Sun Weiguo, Mao Tong'en, et al. China Mainland Moho Boundary Depth Map[J]. Acta Seismologica Sinica, 1995(3): 322-327. |
| [7] | Watts B. Isostasy andFlexures of Lithosphere[M]. Cambridge: Cambridge University Press, 2001. |
| [8] | Geiger L. Probability Method for the Determination of Earthquake Epicenters from Arrival Time Only[J]. Bull St Louis Univ, 1912, 8: 60-71. |
| [9] | Nelson D, John V. Earthquake Locations by 3-D Fi-nite-Difference Travel Times[J]. Bull Seism Soc Am, 1990, 80(2): 395-410. |
| [10] | Prugger F, Gendzwill J. Microearthquake Location:A Nonlinear Approach that Makes Use of a Simplex Stepping Procedure[J]. Bull Seism Soc Am, 1988, 78(2): 799-815. |
| [11] | Douglas A. Joint Epicenter Determination[J]. Na-ture, 1976, 215: 45-48. |
| [12] | Pujol J. Joint Event Location:The JHD Technique and Applications to Data from Local Seismic Networks[C]//Thurber C, Rabinowitz N. Advances in Seismic Event Location.[S. l.]:Kluwer Academic Publishers, 2000:163-204. |
| [13] | Crosson R S. Crustal Structure Modeling of Earth-quake Data:1:Simultaneous Least Squares Estimation of Hypocenter and Velocity Parameters[J]. J Geophys Res, 1976, 81(17): 3036-3046. DOI:10.1029/JB081i017p03036 |
| [14] | Aki K, Lee K. Determination of Three-Dimensional Velocity Anomalies Under a Seismic Array Using First P Arrival Times from Local Earthquakes:Part 1:A Homogeneous Initial Model[J]. J Geophys Res, 1976, 81(23): 4381-4399. DOI:10.1029/JB081i023p04381 |
| [15] | Aki K, Christoffersson A, Eystein H. Determination of the Three-Dimensional Seismic Structure of the Lithosphere[J]. J Geophys Res, 1977, 82(2): 277-296. DOI:10.1029/JB082i002p00277 |
| [16] |
朱元清, 石耀霖, 李平. 一种确定地震深度的新方法[J].
地震地磁观测与研究, 1990, 11(2): 4-12.
Zhu Yuanqing, Shi Yaolin, Li Ping. A New Method to Determine Earthquake Depth[J]. Seismological and Geomagnetic Observation and Research, 1990, 11(2): 4-12. |
| [17] | Thurber C H. Nonlinear Earthquake Location:Theo-ry and Examples[J]. Bull Seism Soc Am, 1985, 75(3): 779-790. |
| [18] | Billing S D, Sambridge M S, Kennet B L N. Errors in Hypocenter Location:Picking, Model, and Magnitude Dependence[J]. Bull Seism Soc Am, 1994, 84(6): 1978-1990. |
| [19] | Waldhauser F, Ellsworth W L. A Double-Difference Earthquake Location Algorithm:Method and Application to the Northern Hayward Fault, California[J]. Bull Seism Soc Am, 2000, 90(6): 1353-1368. DOI:10.1785/0120000006 |
| [20] |
林怀存. 山东地区近震地震波速与地壳结构[J].
华北地震科学, 1989(3): 82-90.
Lin Huaicun. Local Seismic Velocity and Crust Model of Shandong Area[J]. North China Earthquake Sciences, 1989(3): 82-90. |
| [21] |
李铂, 崔鑫, 叶庆东, 等. 山东地区地震波一维速度模型研究[J].
华北地震科学, 2012(4): 1-6.
Li Bo, Cui Xin, Ye Qingdong, et al. Seismic One-Dimension Velocity Model Research[J]. North China Earthquake Sciences, 2012(4): 1-6. |
| [22] |
黄建平, 傅容珊, 许萍, 等. 利用重力和地形观测反演中国及临区地壳厚度[J].
地震学报, 2006, 28(3): 250-258.
Huang Jianping, Fu Rongshan, Xu Ping, et al. Inversion of Gravity and Topography Data for the Crust Thickness of China and Its Adjacency[J]. Acta Seismologica Sinica, 2006, 28(3): 250-258. |
| [23] |
孙耀庭, 徐守余, 张世奇, 等. 山东昌乐凹陷油页岩地球化学特征及成因探讨[J].
吉林大学学报(地球科学版), 2015, 45(3): 736-742.
Sun Yaoting, Xu Shouyu, Zhang Shiqi, et al. Geochemical Characteristics and Genesis of the Oil Shale in Changle Sag of Shandong Province[J]. Journal of Jilin University(Earth Science Edition), 2015, 45(3): 736-742. |
| [24] |
王淑萍, 徐守余, 董春梅, 等. 东营凹陷民丰洼陷北带沙四下亚段深层天然气储层成岩作用[J].
吉林大学学报(地球科学版), 2014, 44(6): 1747-1759.
Wang Shuping, Xu Shouyu, Dong Chunmei, et al. Diagenesis Characteristics of Deep Natural Gas Reservoirs in Es4x in the North Zone of Minfeng Sag in Dongying Depression[J]. Journal of Jilin University (Earth Science Edition), 2014, 44(6): 1747-1759. |
| [25] |
代杰瑞, 喻超, 张杰, 等. 山东半岛蓝色经济区土壤有机碳储量及固碳潜力分析[J].
吉林大学学报(地球科学版), 2014, 44(5): 1659-1668.
Dai Jierui, Yu Chao, Zhang Jie, et al. Analysis on Soil Organic Carbon Storage and the Potential for Carbon Sequestration in the Blue Economic Zone of Shandong Peninsula[J]. Journal of Jilin University(Earth Science Edition), 2014, 44(5): 1659-1668. |
| [26] |
黄超, 余朝华, 张桂林, 等. 郯庐断裂中段新生代右行走滑位移[J].
吉林大学学报(地球科学版), 2013, 43(3): 820-832.
Huang Chao, Yu Chaohua, Zhang Guilin, et al. Cenozoic Dextral Strike-Slip Displacement of the Middle Tan-Lu Fault Zone[J]. Journal of Jilin University(Earth Science Edition), 2013, 43(3): 820-832. |
| [27] |
邱毅, 金星, 蔡辉腾, 等. 利用人工地震研究福建地壳一维速度结构[J].
地震工程与工程振动, 2014, 34(增刊1): 1071-1076.
Qiu Yi, Jin Xing, Cai Huiteng, et al. Fujian Crustal One-Dimension Velocity Model Using Artificial Earthquakes[J]. Earthquake Engineering and Engineering Dynamics, 2014, 34(Sup.1): 1071-1076. |
| [28] |
王小娜, 于湘伟, 章文波, 等. 龙门山断裂带南段地壳一维P波速度结构[J].
地震研究, 2015, 38(1): 16-24.
Wang Xiaona, Yu Xiangwei, Zhang Wenbo, et al. 1D P Wave Velocity in the South Segment of Longmenshan Fault Zone[J]. Journal of Seismological Research, 2015, 38(1): 16-24. |
| [29] |
范玉兰, 林纪曾, 胡瑞贺, 等. 华南地区近震走时表的研制[J].
华南地震, 1990, 10(2): 1-16.
Fan Yulan, Lin Jizeng, Hu Ruihe, et al. The Development of Travel Time Table for Near Earthquake in South China[J]. South China Seismological Journal, 1990, 10(2): 1-16. |


