0 引言
自然科学或工程科学中的数据,无论是来自实际测量还是数值建模,经常会遇到如下几种情况:数据的长度过短,数据是非稳态的,以及数据表示的是某种非线性的函数关系[1]。这几种情况往往相伴发生,并不独立存在。地震数据本质上是非稳态的,其非稳态性主要是由于地震波在地层介质传播过程中的衰减和频散引起的。而从二维和三维的角度来看,地震信号也会受到地层倾角变化及断层等地质构造的影响而表现出非稳态性[2]。这种非稳态性具体表现为地震波的能量随时间和频率剧烈变化,且前者与后两者都不成线性关系。了解不同时间深度上地震波的频率成分对分析地下介质的构造、岩性等信息[3]以及预测油气藏[4]都具有重要的意义。为了解决这个问题,一个最基本的想法就是将地震信号分解为多个稳态的子成分信号,再对这些子信号进行分析。例如,经典的傅里叶变换可以将一维地震数据分解成为多个具有固定频率、相位和振幅的正弦波线性组合;但这种描述能量和频率关系的方式并不能给出能量在时间轴上的分布,不能精细地描述地震信号的非稳态性。随着短时傅里叶变换[5]、小波变换[6-7]、S变换[8-9]、局部时频分解(LTFD)[10-11]等一系列时频分析方法的引入,一维地震数据可以被表示为二维能量关于时间和频率的联合分布,从而直观地分析地震波的能量随时间和频率的变化。本质上,这些传统方法均用提前定义的、具有一定时频局部性的基函数(如傅里叶基、小波基等)来表示地震信号,或者说将地震信号分解为这些基函数的线性组合。所以,这些方法能否较好地刻画地震信号时频属性的关键在于信号固有的时频属性是否与选取的基函数所匹配。但到目前为止,仍无法选择出一种适用所有地震信号的具有较高时频聚焦性的基函数。
从信号处理中稀疏表示的角度分析,传统时频分析方法的局限性是因为在预先设定的基函数上无法对信号进行最稀疏的表示。换句话说,这些传统时频分析方法虽然也是一种分解,但分解出来的子成分过于冗余。解决上述问题的一种办法是从待分解的地震信号自适应地提取出能够稀疏表示该信号的基函数,并用这组基函数对信号进行表示。这些基函数具有一定的时频局部性。Huang等[1]提出了经验模式分解(EMD),将一维非稳态信号自适应地分解为一系列具有稳态特征的本征模函数(IMF)。这些本征模函数既可以被看作是表示信号的基函数,也可以被视为信号的子成分。对分解得到的每个IMF进行希尔伯特变换,可以得到具有明确物理意义的瞬时频率,从而得到信号能量的瞬时谱,实现信号的时频属性描述。很多地球物理学者已经将EMD及其改进方法(如EEMD和CEEMD等)引入到地震信号的处理和分析中[12-15]。但这类基于EMD的时频分解方法仍是基于经验的归纳,暂时缺乏数学理论上的支持[16]。
本文首次引入一种新的经验性时频分析方法——局部均值分解(local mean decomposition,LMD)来表征地震信号的时频变化。该方法是2005年由Smith[17]提出的一种基于迭代的自适应时频分解方法。与EMD类似,LMD也是通过不断迭代直到找到一个符合要求的子成分,并将该子成分从之前的信号中减去,若干次后,原信号都可以表示为分解所得的若干个子成分的和。但在每次迭代寻找符合要求的子成分时,LMD是通过不断地从原始信号中分离出调频信号和包络信号直至分解得到一个近似的标准调频信号,这与传统的EMD类方法有明显区别,这种分解的方式更恰当,也更能体现信号的本质[18]。通过LMD分解方法对模拟信号和叠后地震数据进行分析,并对比EMD方法,发现LMD分解更合理,受端点效应的影响更小。通过对分解得到的各乘积函数(product function,PF)求取瞬时频率,最终构建出更符合地震信号时频属性的瞬时谱。利用LMD分解得到的不同分量地震剖面,可以从不同时间尺度分析地震数据的非稳态特征,进而用于预测油气储层的位置。
1 局部均值分解LMD方法自提出以来,主要被用来分析非稳态信号,如脑电波信号(EEG)、机械故障信号等[17, 19]。这种方法与EMD相似,都是用迭代的方式从信号中提取出若干个近似于单频或窄频带的稳态信号,分解之后再求取瞬时频率,避免直接对原信号求取瞬时频率时出现的某些从物理意义上无法解释的情况,如负频率等。但从对信号分解的角度,两者也存在本质的差别。在EMD的每次迭代过程中,需要对上次迭代得到的残差信号的各个极大值点和极小值点进行三次样条插值,构建残差信号的上包络和下包络函数,从而得到均值函数,然后将之从残差信号中减去。LMD方法认为这种三次样条插值的方式不利于刻画信号的细节,而是先构建局部均值函数和局部包络函数,再通过滑动平均的方式进行平滑,直至相邻两点的值都不相同。
设待分解信号为f (t),其第i个局部极值点为f (ti),则通过相邻的局部极值可以确定局部均值函数m (t)和局域包络函数a (t):
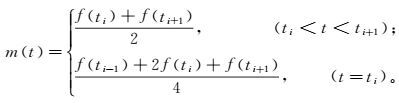 (1)
(1) 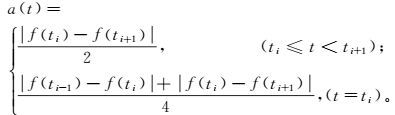 (2)
(2) 式中,ti代表第i个极值点所对应的时刻。为了避免端点效应,一般分别将信号向两端延拓1~3个极值点[20];然后通过滑动平均对得到的局部均值函数和局域包络函数(如式(1)、(2) 所示)进行平滑处理,直到任意相邻点的值都不相同。
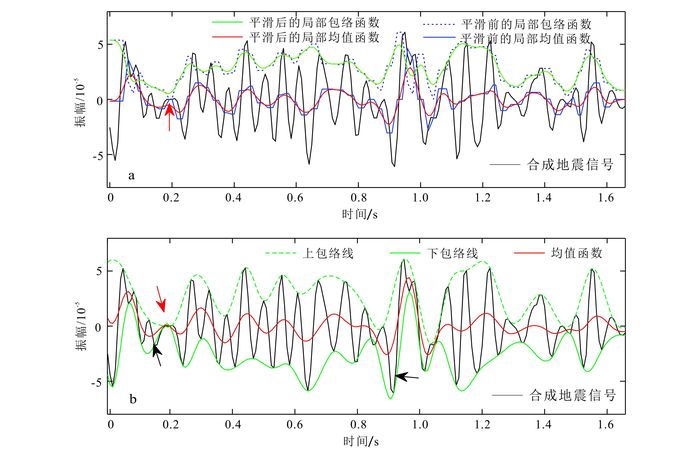
选取一道合成地震记录f(t)(图 1),显然其具有非稳态特性。可以计算该信号滑动平均前的局部均值函数和局部包络函数以及滑动平滑处理后最终的局部均值函数和局部包络函数(图 1a)。为了对比,显示EMD方法中所需的上包络线和下包络线,其均值函数即为两者的平均值(图 1b)。可以看出,EMD方法中的上包络线和下包络线会出现过包络和欠包络的现象(图 1b中黑色箭头处),从而导致求出的均值函数有时并不能合理地描述信号的均值。在某些位置上,均值函数与上、下包络线重合在一起(图 1b中红色箭头处),而对应位置LMD计算的局部均值函数(图 1a中红色箭头处)则较好地反映了该位置信号的均值。所以,LMD对均值函数和包络函数的描述能更好地反映信号的局部特征。需要注意的是,LMD中的局部包络函数与EMD中的上、下包络函数意义不同:前者是在迭代过程中通过局部包络函数到达解调信号,有着独立的意义;而后者只为了计算均值函数。
|
| 图 1 LMD方法中的局部均值函数和局部包络函数(a)及EMD方法中的上下包络函数及对应的均值函数(b) Figure 1 Mean function and envelop function of LMD (a) and EMD (b) |
|
|
局部均值分解方法的具体步骤如下:
1) 输入待分解地震信号f (t),依照公式(1)、(2) 计算其局部均值函数m (t)和局部包络函数a (t)。
2) 将得到的局部均值函数从待分解信号中分离出来,然后除以局部包络函数,得到待分解信号解调过程中的近似调频信号s (t)。
3) 若此时s (t)不是一个标准调频信号(a (t)≠1),则用s (t)代替原来的待分解信号,按照步骤1) — 2) 不断迭代n次,直到得到的结果sn(t)接近标准调频信号,即-1≤sn(t)≤1,并且包络函数an(t)≈1。此时可以得到
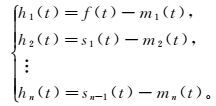 (3)
(3) 其中
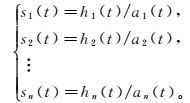 (4)
(4) 4) 将迭代过程中所有平滑的局部包络函数相乘得到最后的包络信号:
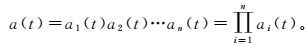 (5)
(5) 5) 将上述包络信号和最后得到的标准调频信号相乘,得到一个乘积函数,记做PF1(t):
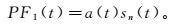 (6)
(6) 这里的PF1(t)就是一个信号分解出来的子成分,也可以称为PF分量。
6) 将5) 中所得的PF分量从原信号中减去,记做新的残差函数r (t),即
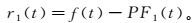 (7)
(7) 将残差r1(t)作为新的信号进行分解(即公式(3) —(7)),多次迭代,直到rk(t)为一个单调函数或能量小于某个提前设定的阈值为止。此时,原信号即可表示为
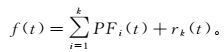 (8)
(8) 公式(3) —(4) 实际上是将信号不断解调的过程,类似EMD中的筛选(sifting)过程。因为LMD分解所得的若干个PF分量与EMD方法所得的IMF分量在物理意义上较为接近,因此可以采用希尔伯特变换求出各PF分量的瞬时频率,从而得到信号的瞬时谱。但是由希尔伯特变换求取的瞬时频率往往在信号的端点位置出现较剧烈的抖动,并且有时出现负的瞬时频率值。
针对LMD方法的特点,可以采用另一种求取瞬时频率的方法。因为在每次分解出PF分量的同时,也得到了这个PF分量对应的近似标准调频信号和包络函数。式(6) 中每个PF分量对应的标准调频信号可以写作
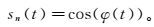 (9)
(9) 式中,φ(t)为瞬时相位。而对这个标准调频信号求反余弦函数可以得到瞬时相位,对应的瞬时频率为对瞬时相位求导:
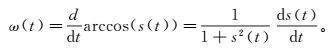 (10)
(10) 结合该PF分量对应的包络函数a (t),即可写出其包络值关于时间和频率的联合函数,记作a (ω, t)。而信号的瞬时谱[13]则为分解所得的PF分量包络联合函数之和,即
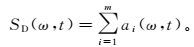 (11)
(11) 这时的瞬时谱在时频平面上较为稀疏,为了与传统的时频谱对应起来,一般对得到的瞬时谱做高斯滤波[13, 17]。
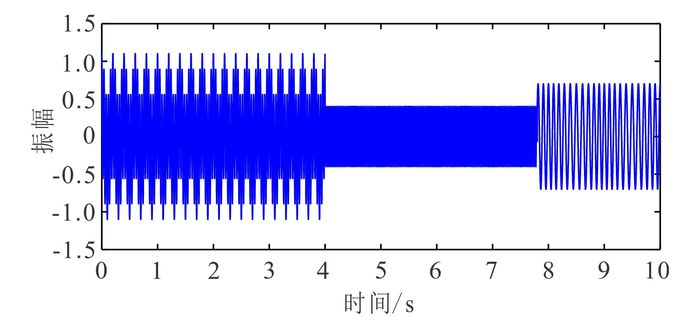
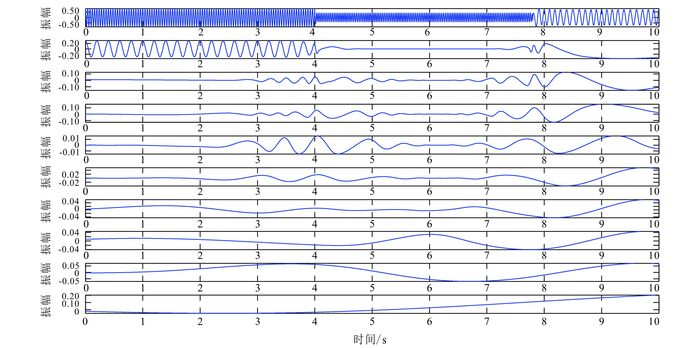
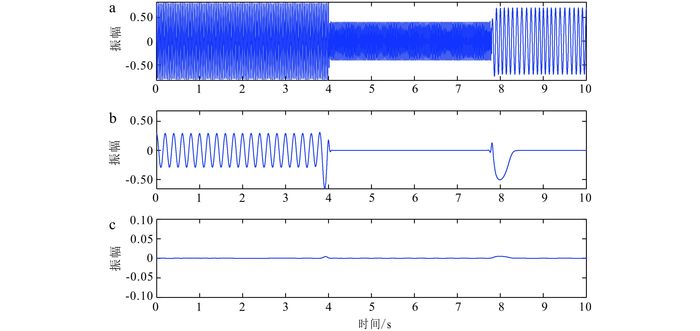
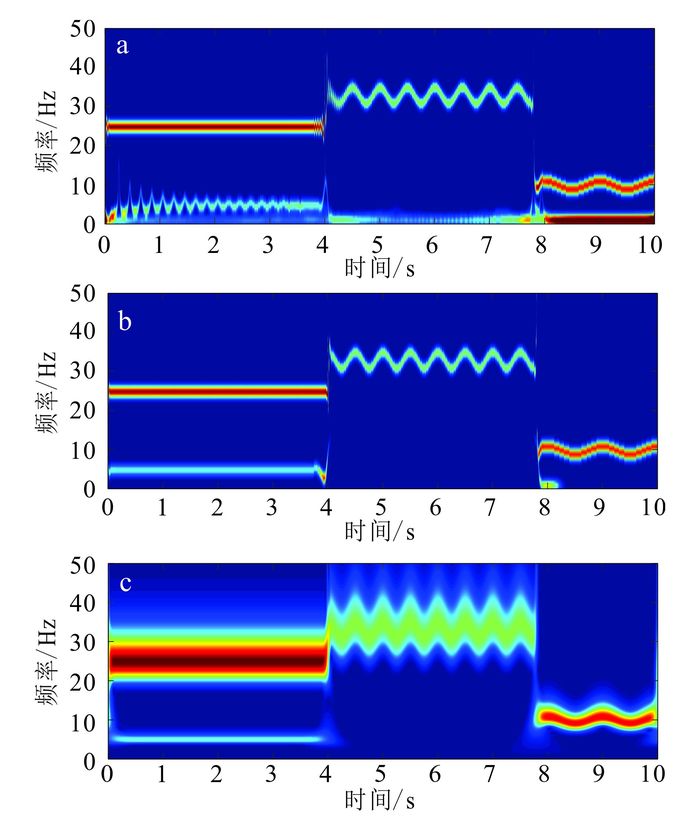
2 模型测试为了测试LMD分解非稳态信号的合理性和有效性,首先构造了类似Herrera等[21]在其文章中构造的模拟信号(图 2)。该信号由不同频率的谐波成分组成,其每一个子成分存在于不同的时间区间。对其分别应用EMD和LMD方法进行分解。从得到的分解结果(图 3和图 4)可以看出:EMD和LMD方法都可以将信号的主要特征表现出来,但EMD方法分解出来很多不符合原信号物理意义的虚假成分(图 3),这主要是EMD采用三次样条插值的方式不能较准确地估计包络信号的原因;而图 4中LMD方法分解出来的PF分量能较好地符合原信号的物理意义。这也可以从基于两种方法求得的时频谱(图 5a、b)来观察:EMD方法分解所得的虚假子成分导致求得的时频谱不如基于LMD方法求得的时频谱准确,这同时也影响了时频谱的分辨率。图 5c为基于S变换求出的时频谱,经与图 5b对比可以看出,基于LMD方法求出的时频谱分辨率比基于S变换求出的更高。
|
| 图 2 不同的谐波成分合成的模拟信号 Figure 2 Synthetic signal composed of several harmonics |
|
|
|
| 图 3 模拟信号经EMD方法分解所得的各阶IMF分量 Figure 3 IMFs of the synthetic signal generated by EMD method |
|
|
|
| 图 4 模拟信号经LMD方法分解得到的PF分量(a、b)及残差(c) Figure 4 PFs of the synthetic signal generated by the LMD method |
|
|
|
| a.基于EMD方法;b.基于LMD方法;c.基于S变换。 图 5 模拟信号时频谱 Figure 5 Time-frequency spectrum of the synthetic signal |
|
|
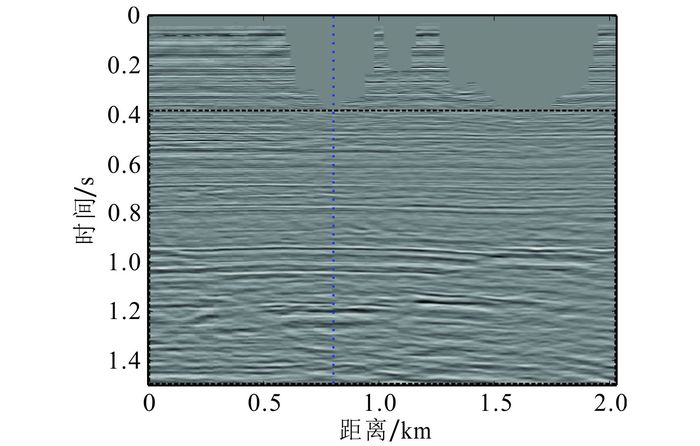
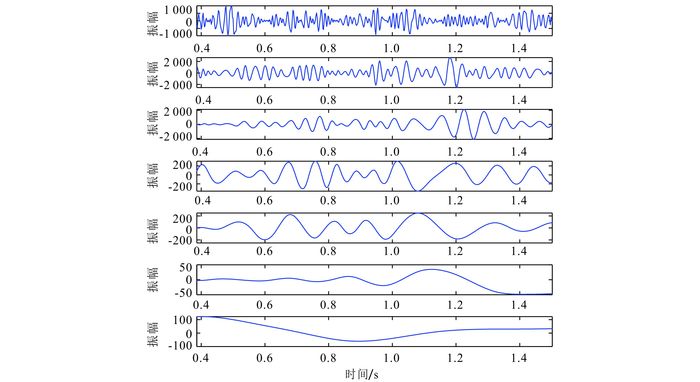
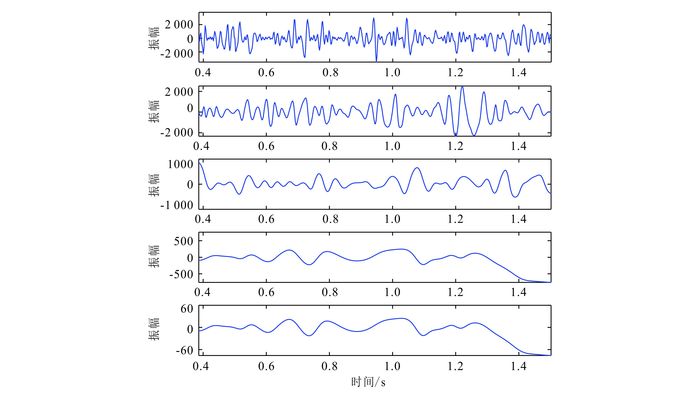
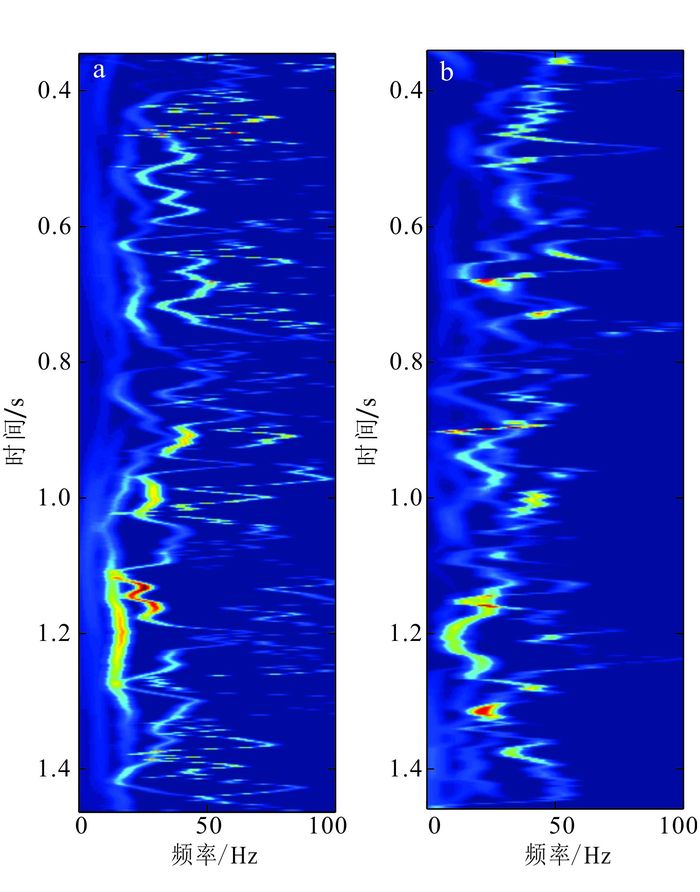
为了进一步验证本文方法分解地震数据的有效性,选取了一个海上叠后地震数据[22](图 6)进行测试,对每一道分别应用EMD和LMD进行分解。首先选取第80道地震数据(图 6中蓝色虚线),并对其分别应用LMD和EMD方法进行分解,结果如图 7和图 8所示。可以看出,两者的分解结果正好阐释了IMF分量和PF分量从定义角度上的本质区别:IMF分量更强调上下包络对称;而PF分量则保留了更多信号的局部信息,是一种更自然的分解方式。由两种方法的分解结果求出的时频谱如图 9所示。
|
| 图 6 海上叠后地震数据 Figure 6 A field marine seismic data set |
|
|
|
| 图 7 第80道地震数据经EMD方法分解所得的IMF分量 Figure 7 IMFs generated by the EMD method of one seismic trace |
|
|
|
| 图 8 第80道地震数据经LMD方法分解所得的PF分量 Figure 8 PFs generated by the LMD method of one seismic trace |
|
|
|
| a.基于EMD方法;b.基于LMD方法。 图 9 第80道地震数据的时频谱 Figure 9 Time-frequency spectrum of one seismic trace |
|
|
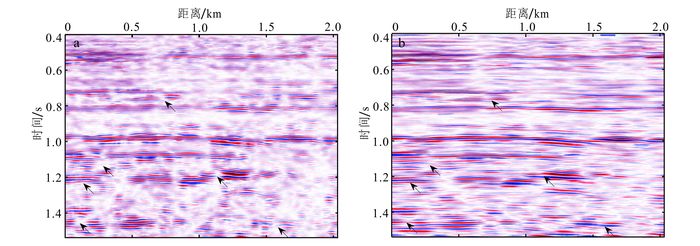
对图 6叠后地震资料逐道应用两种方法分解,每一道都可以得到从高频到低频的各阶分量信号,其中前三阶子成分是主要成分。将前三阶分量组合在一起即可得到该数据的前三阶子成分剖面,应用EMD和LMD提取了前三阶分量剖面(图 10—12)。因为LMD和EMD方法都只考虑单道,并不考虑地震数据水平方向的连续性,所以在水平方向会出现个别不连续的点;这时沿着不同地震道方向应用简单的均值滤波即可消除。
|
| 图 10 基于EMD方法(a)和LMD方法(b)分解得到的第一阶子成分剖面 Figure 10 First order component profiles generated by EMD method (a) and LMD method (b) |
|
|
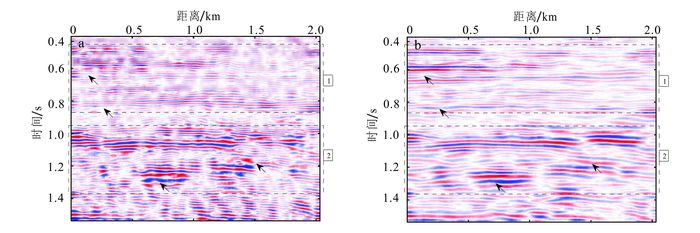
|
| 图 11 基于EMD方法(a)和LMD方法(b)分解得到的第二阶子成分剖面 Figure 11 Second order component profiles generated by EMD method (a) and LMD method (b) |
|
|
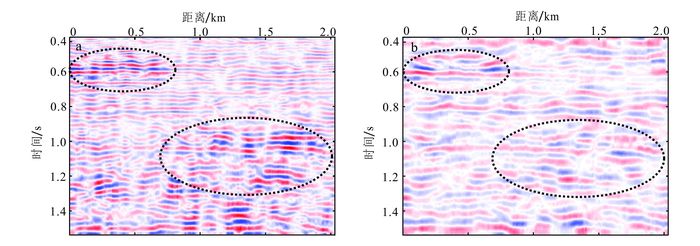
|
| 图 12 基于EMD方法(a)和LMD方法(b)分解得到的第三阶子成分剖面 Figure 12 Third order component profiles generated by EMD method (a) and LMD method (b) |
|
|
图 10为EMD和LMD方法分解出的第一阶分量剖面,都为高频部分,主要反映地震资料中的一些细节信息和高频噪声。从图 10a、b的对比来看,LMD方法分解出的第一阶剖面更加连续,分辨率更高(如箭头所指位置所示)。而第二阶分量剖面(图 11)反映了地震资料的主要反射层,较第一阶剖面更加明显。通过对比第二阶剖面可以发现:EMD在浅层(如图 11a方框1所示)频率较高,深层(如图 11a方框2所示)频率较低,存在一定差异;而LMD在浅层(如图 11b方框1所示)和深层(如图 11b方框2所示)较为一致,均在同一个时间尺度下。从图 12我们发现,EMD方法将一部分本应集中在第二阶分量剖面的主要反射层信息分解到第三阶分量剖面里(图 12a椭圆位置);而LMD方法分解的第二阶分量剖面能较完整地突显出主要反射层的形态,且更加连续,这与LMD方法能更好地避免模态混叠有关。
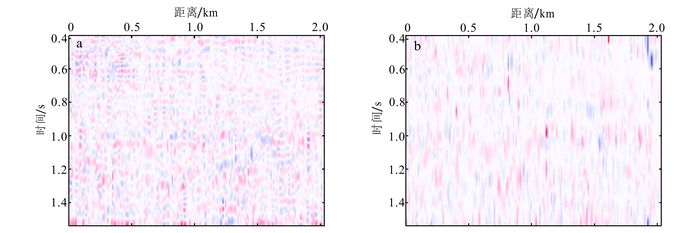
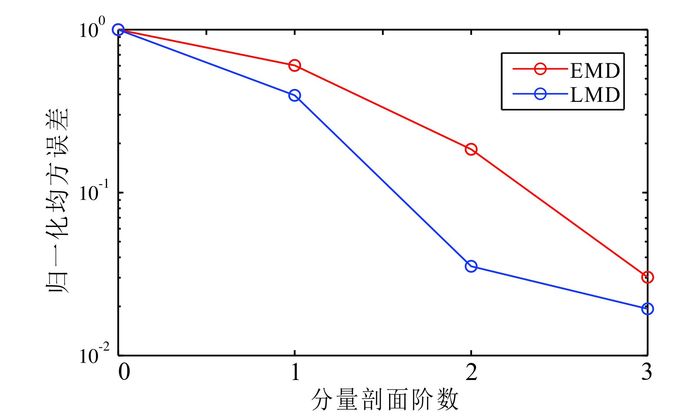
图 13是原地震资料减去前三阶分量剖面的残差剖面,可以看出:LMD方法分解得更加彻底,残留的基本是噪音;而EMD方法分解后的残差仍残留部分有效信息。图 14为基于EMD和LMD方法依次分解出前三阶分量剖面后残差剖面与原地震资料相比的归一化均方误差,可以看出:在对地震资料的分解过程中,随着分解出分量剖面数的增加,残差剖面的能量逐渐减小。对比分离出相同阶分量剖面后残差剖面的误差可以发现,LMD方法较EMD方法分解得更加彻底。此外,LMD方法在分解出第二个剖面后,残差剖面能量下降较EMD方法更快;参照之前对图 11和图 12的分析,说明LMD方法提取的第二阶分量剖面更加合理,更符合地震信号固有的时频属性。
|
| 图 13 基于EMD方法(a)和LMD方法(b)分解后的残差剖面 Figure 13 Residual profiles generated by EMD method (a) and LMD method (b) |
|
|
|
| 图 14 基于EMD和LMD方法依次得到前三阶分量剖面的归一化均方误差 Figure 14 Normalized mean square error of the decomposition by EMD method and LMD method |
|
|
LMD方法是一种基于EMD方法发展而来的新的时频分解方法,它的出发点在于从原信号中更加合理地自适应分解出符合信号固有时频属性的稳态子波成分,同样属于一种经验分解方法。该方法在每次迭代中能够更加合理地描述地震信号的局部细节,分解结果更符合其固有时频属性,能够更稀疏地表示地震信号。所以基于LMD方法的稳态地震子波时频谱也更加精确,同时这些子成分组成的各阶剖面也更连续和具有解释意义。
本次研究讨论了LMD方法在时频分解、瞬时属性提取以及地震资料模态分离中的应用,为分析非稳态地震信号的局部时频变化提供了有效工具,也为进一步的地震数据处理和目标解释,如去噪、构造识别和储层预测等,提供了可供选择的基础理论和方法。
| [1] | Huang N E, Shen Z, Long S R, et al. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis[J]. Proceedings of the Royal Society of London:Series A:Mathematical, Physical and Engineering Sciences, 1998, 454: 903-995. DOI:10.1098/rspa.1998.0193 |
| [2] | Fomel S. Seismic Data Decomposition into Spectral Components Using Regularized Nonstationary Autoregression[J]. Geophysics, 2013, 78(6): O69-O76. DOI:10.1190/geo2013-0221.1 |
| [3] | Liu J, Marfurt K. Instantaneous Spectral Attributes to Detect Channels[J]. Geophysics, 2007, 72(2): P23-P31. DOI:10.1190/1.2428268 |
| [4] | Ebrom D. The Low-Frequency Gas Shadow on Seismic Sections[J]. The Leading Edge, 2004, 23(8): 772. DOI:10.1190/1.1786898 |
| [5] | Gabor D. Theory of Communication[J]. Journal of the Institute of Electrical Engineers, 1946, 93(26): 429-441. |
| [6] | Chakraborty A, Okaya D. Frequency-Time Decom-position of Seismic Data Using Wavelet-Based Methods[J]. Geophysics, 1995, 60(6): 1906-1916. DOI:10.1190/1.1443922 |
| [7] | Sinha S, Routh P, Anno P, et al. Spectral Decom-position of Seismic Data with Continuous Wavelet Transform[J]. Geophysics, 2005, 70(6): P19-P25. DOI:10.1190/1.2127113 |
| [8] | Pinnegar C R, Mansinha L. The S-Transform with Windows of Arbitrary and Varying Shape[J]. Geophysics, 2003, 68(1): 381-385. DOI:10.1190/1.1543223 |
| [9] | Stockwell R G, Mansinha L, Lowe R P. Localization of the Complex Spectrum:The S Transform[J]. IEEE Transactions on Signal Processing, 1996, 44(4): 998-1001. DOI:10.1109/78.492555 |
| [10] | Liu Y, Fomel S. Seismic Data Analysis Using Local Time-Frequency Decomposition[J]. Geophysical Prospecting, 2013, 61(3): 516-525. DOI:10.1111/gpr.2013.61.issue-3 |
| [11] |
刘洋, 李炳秀, 刘财, 等. 局部时频变换域地震波吸收衰减补偿方法[J].
吉林大学学报(地球科学版), 2016, 46(2): 594-602.
Liu Yang, Li Bingxiu, Liu Cai, et al. Attenuation Compensation Method of Seismic Wave in the Local Time-Frequency Transform Domain[J]. Journal of Jilin University (Earth Science Edition), 2016, 46(2): 594-602. |
| [12] | Chen Y, Fomel S. Emd-Seislet Transform[C]//SEG New Orleans 2015 Annual Meeting. New Orleans:SEG, 2015:4775-4778. |
| [13] | Han J, Baan M V D. Empirical Mode Decomposition for Seismic Time-Frequency Analysis[J]. Geophysics, 2013, 78(2): O9-O19. DOI:10.1190/geo2012-0199.1 |
| [14] | Pi H, Liu C, Wang D. Using Hilbert-Huang Trans-form to Pick up Instantaneous Parameters of Seismic Signal[J]. Oil Geophysical Prospecting, 2007, 42(4): 418-424. |
| [15] | Wen X, He Z, Huang D. Reservoir Detection Based on EMD and Correlation Dimension[J]. Appl Geophys, 2009, 6(1): 70-76. DOI:10.1007/s11770-009-0002-5 |
| [16] | Wu Z, Huang N E. Ensemble Empirical Mode De-composition:A Noise-Assisted Data Analysis Method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41. DOI:10.1142/S1793536909000047 |
| [17] | Smith J S. The Local Mean Decomposition and Its Application to EEG Perception Data[J]. Journal of the Royal Society Interface, 2005, 2(5): 443-454. DOI:10.1098/rsif.2005.0058 |
| [18] | Dai H, Xu A. A Comparative Study on Estimation of Instantaneous Frequency by Means of Lmd[C]//IEEE International Conference on Information and Automation. Yinchuan:IEEE, 2013:964-969. |
| [19] | Wang W, Zhang W H, Han J G, et al. A New Wind Turbine Fault Diagnosis Method Based on the Local Mean Decomposition[J]. Renewable Energy, 2012, 48(6): 411-415. |
| [20] |
程军圣, 张亢, 杨宇. 基于噪声辅助分析的总体局部均值分解方法[J].
机械工程学报, 2011, 47(3): 55-62.
Cheng Junsheng, Zhang Kang, Yang Yu. Ensemble Local Mean Decomposition Method Based on Noise-Assisted Analysis[J]. Chinese Journal of Mechanical Engineering, 2011, 47(3): 55-62. |
| [21] | Herrera R H, Tary J B, Baan MV D. Time-Fre-quency Representation of Microseismic Signals Using the Synchrosqueezing Transform[C]//Geoconvention. Calgary:CSEG, 2013: |
| [22] | Liu G, Fomel S, Chen X. Time-Frequency Analysis of Seismic Data Using Local Attributes[J]. Geophysics, 2011, 76(6): P23-P34. DOI:10.1190/geo2010-0185.1 |



