0 引言
地-井瞬变电磁法是在地面敷设不接地回线,供以阶跃电流,在钻孔中观测电流关断后的感应二次场,通过解释分析二次场的变化,获得钻孔附近隐伏导体的位置等信息,是深部找矿较有前景的方法之一[1]。
国内外对地-井瞬变电磁方法的数值研究主要集中于三维正演模拟,以获得典型异常的瞬变响应特征,指导数据解释工作[2]。较为经典的工作是基于等效薄板的半解析方法,以及基于灯丝等效的近似方法[3-5]。West等[6]使用积分方程法研究了三维断裂构造钻孔中的瞬变电磁响应。李建慧等[7]、徐正玉[8]和杨海燕等[9-10]分别应用矢量有限单元法和时间域有限差分法完成了地面回线激发的地-井瞬变电磁三维正演。
本文给出了一种全空间[11]、适合水平地形下导电体的三维瞬变电磁模拟技术,并将其应用到地-井瞬变电磁的三维数值模拟中。首先,在频率域采用交错网格有限差分法求解基于二次电场的赫姆霍兹方程。在此过程中,应用MUMPS数学软件包求解离散方程;用虚拟方格叠加方法计算矩形发射源产生的背景场,用圆形回线等效每个虚网格,并采用虚拟界面法解决全空间格林函数的计算。然后,利用余弦变换方法将各测点的频率响应转换为瞬变电磁响应。算法精度用均匀半空间解析解与前人三维局部异常体模型进行对比验证。最后,给出均匀半空间和三维低阻薄板模型垂直磁场响应的三维分布,并分析不同井位瞬变电磁响应随深度的变化规律。
1 地-井瞬变电磁三维交错网格有限差分正演 1.1 频率域有限差分正演为了克服地面矩形大定源电磁法在数值模拟过程中源描述的困难以及源奇异性对数值稳定性的影响,三维正演数值模拟针对异常二次电场进行[12-13]。忽略位移电流,二次场可以表示为
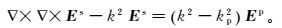 (1)
(1) 式中:Es为二次场;k和kp分别为真空中和背景模型的波数;Ep为背景电场。
在x、y、z方向上离散式(1),有
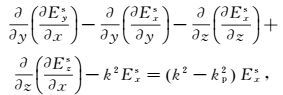 (2)
(2) 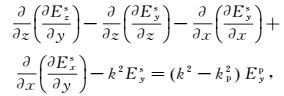 (3)
(3) 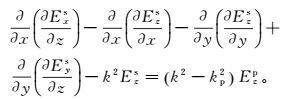 (4)
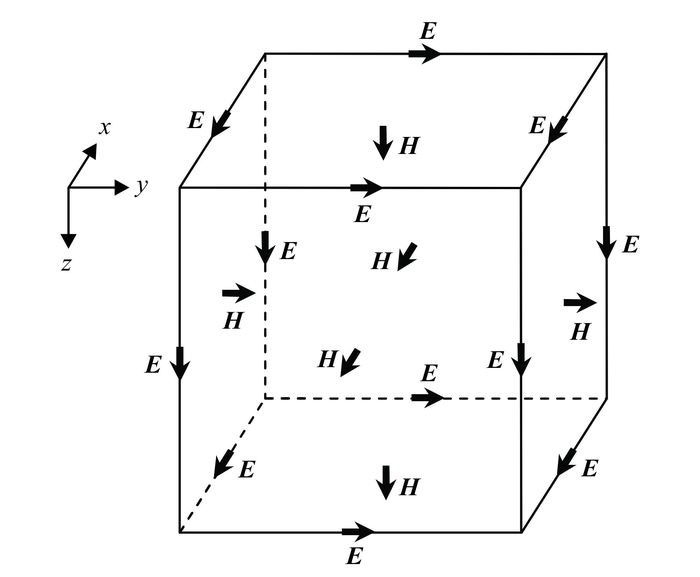
(4) 根据文献[14],我们采用交错网格有限差分技术求解方程(2) —(4) [15]。图 1给出了差分计算中剖分单元的电磁场配置关系,待求解电场位于剖分单元棱边中点,导出的磁场位于棱边包围面积中心。
|
| 图 1 交错网格有限差分计算采用的Yee晶胞格式 Figure 1 A typical Yee grid of staggered-grid finite difference method |
|
|
为了计算介质中的二次电场,将地电模型剖分成长方体网格(包括上面的空气),并用(i, j, k)标注。其中,i、j、k分别表示x、y、z方向的网格序号,i =1~Nx,j=1~Ny,k=1~Nz,Nx、Ny、Nz分别为x、y、z方向的网格数。每一个长方体单元的电阻率为ρ(i, j, k)。以式(2) 为例,在上述差分方案的基础上,以差分代替微分,有如下的近似展开:
 (5)
(5) 式中:Eyi+1, j+1/2, ks为(i+1, j+1/2, k)节点处y方向上的二次场;Exi+1/2, j, kp为(i+1/2, j, k)节点处x方向上的背景场;Δwl(w=x, y, z;l=i, j, k)代表第l个剖分单元在w方向上的长度;Δwl(w=x, y, z;l= i, j, k)为w方向剖分单元l和l-1的中心点距离。经过整理,最终形成如下矩阵方程:
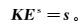 (6)
(6) 式中:K为大型系数矩阵;s包含源项以及边界条件。由于针对二次场进行模拟,当剖分区域足够大时,可以认为计算区域边界上的二次场都衰减到0,满足狄里克雷边界条件[16]。
虽然式(6) 的求解可以采用经典的方法[17-19],但这里我们采用MUMPS求解器直接计算[20]。一旦获得异常电场Es,则各单元棱边总场E=Es+Ep,进而网格单元表面的中心磁场为
 (7)
(7) 式中:ω为角频率;μ0为真空中的磁导率。对于任意的空间位置r,其对应的磁场可以通过对式(7) 的结果进行插值的方法得到,即
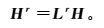 (8)
(8) 式中,Lr为任意的空间位置r磁场空间插值算子。
1.2 背景格林函数在上面的三维模拟方案中需要计算背景场Ep。对于矩形大定源装置,背景格林函数的计算采用Weng等[21]提出的虚框叠加等效方法(图 2),其核心是虚拟方形回线面积等效的圆形回线电磁格林函数的计算。
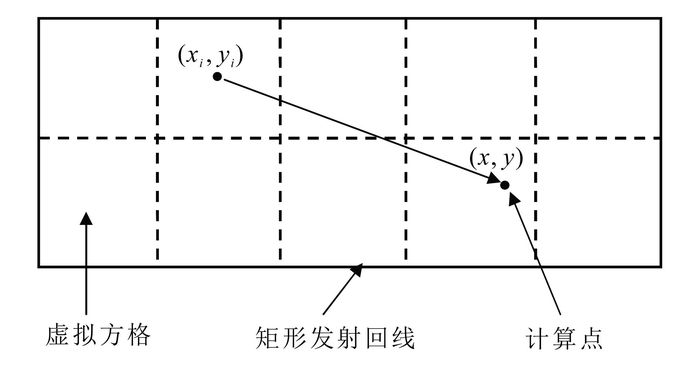
|
| 图 2 矩形大回线源等面积虚拟方形网格剖分原理示意图 Figure 2 Square summation principle in which a rectangular loop is spanned by a certain number of fictitious squares |
|
|
圆形回线层状介质电场格林函数的计算采用虚界面法[21-24]。根据该方法,空间任意一点P(x, y, z)的电场可以表示为
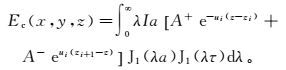 (9)
(9) 式中:λ为波长;I为电流强度;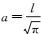
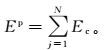 (10)
(10) 式中,N为等面积虚拟方形源数。
利用虚框等效叠加法和虚界面法,发射源可位于任意层位,计算点可扩展到发射回线边界外的空间任意位置,实现了全空间背景格林函数的计算。
1.3 瞬变电磁响应计算以垂直磁场为例,其时间域和频率域之间的关系[2]可以表示为余弦变换:
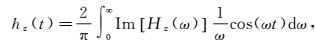 (11)
(11) 或者正弦变换:
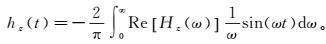 (12)
(12) 式中:Re[Hz(ω)]和Im[Hz(ω)]分别为频率域垂直磁场响应的实部和虚部;t为时间。利用折线逼近法离散式(11) 得
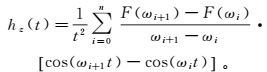 (13)
(13) 式中,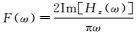
这样,对频率域磁场响应采样,通过式(13) 得到时间域磁场响应,再利用梯形积分,就计算出全空间任意一点的瞬变电磁响应。
2 地-井瞬变电磁响应精度验证 2.1 均匀半空间模型首先设计一个100 Ω·m的均匀半空间模型,发射源为半径等于200 m的圆回线,供电电流为10 A。三维模型x、y和z方向的剖分网格数分别为30、30、10,最小网格尺寸为20 m×20 m×20 m。计算发射回线中心处时间域垂直磁场响应hz(t),结果如图 3所示。从图 3可以看出,本文算法的计算结果与解析解[1-2, 10]具有很好的一致性。

|
| 图 3 均匀半空间模型发射回线中心处垂直磁场响应 Figure 3 Transient electromagnetic (TEM) responses from a homogenerous halfspace model |
|
|
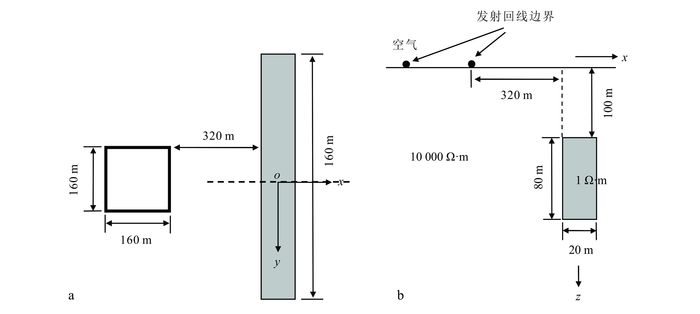
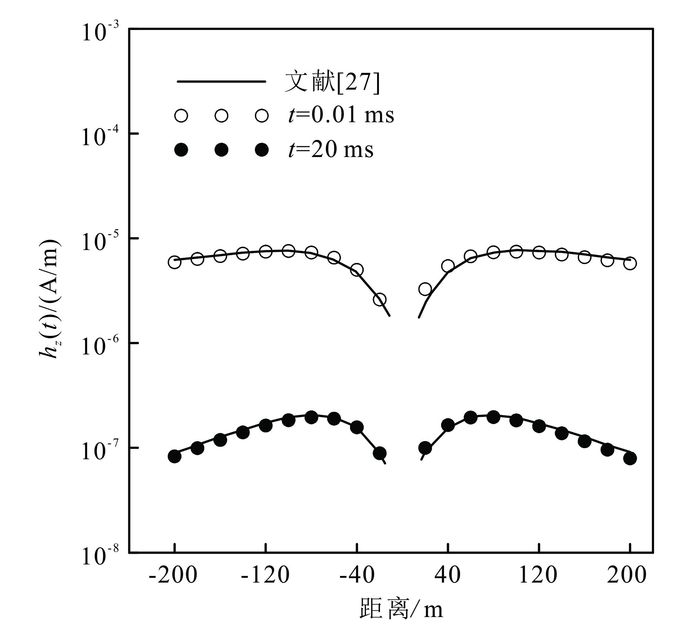
用于检验算法模拟精度的三维模型和Newman等[27]的相同,在100 Ω·m的均匀半空间嵌入一个1 Ω·m三维低阻板体(图 4)。发射源为160 m×160 m的方形回线,水平铺于地表,供电电流为1 A。坐标原点位于异常体中心在地面上的投影位置,z轴向下为正。在x、y和z方向,模型剖分的网格数分别为40、40和25;网格尺寸均匀,为20 m×20 m×20 m。过主剖面选取0.01和20 ms两个时间道的计算结果绘制在图 5中。由图 5可见,本文算法的计算结果与Newman等[27]的结果具有很好的一致性。
|
| 图 5 包含三维低阻异常体的均匀半空间模型地面瞬变电磁剖面响应 Figure 5 TEM responses from a 3D high conductive body buried in a homogeneous earth |
|
|
综上所述,与均匀半空间的解析解和Newman等[27]给出的三维低阻导体模型的数值结果进行对比,充分验证了本文三维算法的正确性。
3 三维瞬变响应特征分析在下面的模拟中,观测系统的发射源为200 m×200 m,位于地表,供电电流为1 A。坐标原点位于发射回线的中心,z轴垂直地表向下为正。为模拟地-井条件,在x、y和z各方向上均匀分布10个计算点,点距均为40 m。三维模拟剖分网格数为40×40×25个,最小网格尺寸为20 m×20 m×20 m。
3.1 均匀半空间模型均匀半空间电阻率为100 Ω·m。图 6给出了过y=20 m的垂直断面内不同延迟的垂直磁场响应。从图 6可见,在早期,断面内的感应磁场以源中心呈对称分布,并且集中在地表附近(图 6a);随着时间延迟,磁场异常中心向深部移动,异常从中心向下向外传播,场强逐渐衰减(图 6b);在晚期,异常中心超出观测深度,在断面内异常被均匀化,并且感应方向向上(图 6c, d)。
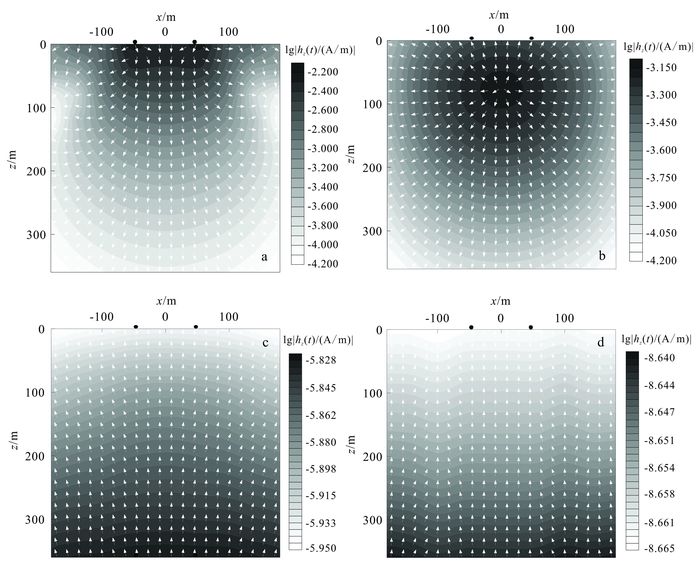
|
|
图中白色箭头为场值梯度方向,黑点为发射源边,下同。 a. t=10-6 s;b. t=6.61×10-5 s;c. t=4.37×10-3 s;d. t=3.55 s。 图 6 均匀半空间模型垂直磁场三维响应主剖面 Figure 6 hz(t) cross-section through source center of a transmitter laid out over a homogeneously conductive earth |
|
|
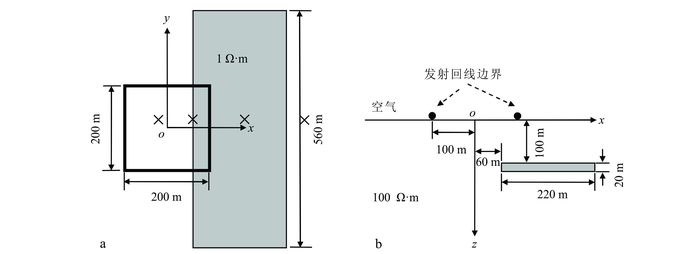
为了进一步验证本文算法的稳定性,设计了如图 7所示的模型,以模拟地-井瞬变电磁方法勘查围岩中赋存金属矿体的情况,并为地-井瞬变电磁数据解释提供理论指导。20 m厚的水平低阻薄板模拟导电矿体。发射源中点与矿体的最小水平距离为60 m。图 8给出了该模型不同时间磁场响应主剖面的断面分布。
|
|
×表示4口井,1号井、2号井、3号井和4号井的坐标分别为(-20, 20)、(60, 20)、(180, 20) 和(350, 20)。 a.平面俯视图;b.切向剖面。 图 7 导电围岩中低阻薄板模型三维模拟装置示意图 Figure 7 Model of 3-D low-resistivity sheet buried in conductive half space |
|
|
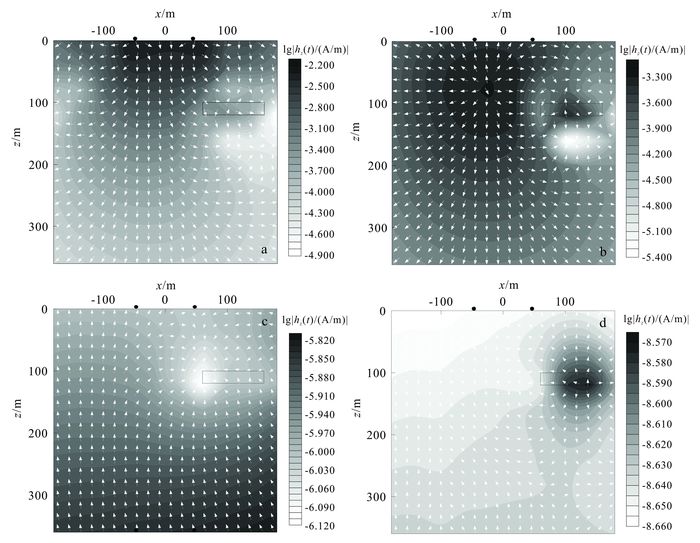
|
|
矩形实线表示异常体位置。 a. t=10-6 s;b. t=6.61×10-5 s;c. t=4.37×10-3 s;d. t=3.55 s。 图 8 均匀半空间嵌入低阻薄板模型垂直磁场三维响应主剖面 Figure 8 Distribution of vertical magnetic field for a conductivity sheet is inserted to homogeneous half-space model |
|
|
从图 8可以看出:在t=10-6 s时,“涡流”位于地表附近,异常体的存在对磁场产生的影响较小,磁场分布与均匀半空间近似(图 8a);随着时间延长,磁场主异常中心向下扩散,但由于低阻薄板的存在,磁场在异常体位置发生畸变(图 8b);在t=4.37×10-3 s时,涡流继续向下扩散,背景场衰减,但由于低阻异常体的集流作用,二次场在板体附近相对增强,并在板体上下方产生强异常中心(图 8c);在t=3.55 s时,导电板体引起的异常可以看成载流导线产生的磁场,并且向外漂移(图 8d)。因此,导电薄板状体的瞬变电磁响应在晚期可以用等效电流线模拟。
矩形发射回线源激发的场以“烟圈”的形式随着时间衰减范围不断扩大,强度减弱;低阻异常体对电磁场有“吸附”性质,低阻体产生的电磁场随着时间延迟衰减较慢。
图 9给出了图 7中4个典型测点井中磁场响应随深度变化的剖面曲线。1号井和4号井位于异常体外侧,2号点位于异常体边缘,3号点井穿过晚期异常体的影响消失,曲线形态与均匀半空间近似。而对于异常体位于发射源和井口中间的情况(4号井),早期导电薄板影响强烈,晚期与1井的磁场响应符号相反(图 9d)。对于靠近和穿过异常体的井孔(2号井、3号井),不同时刻的响应曲线均在异常体位置附近发生畸变,典型特征是中期时间道响应在深度方向极性反转,由正变为负(图 9b、c)。与图 8比较可知,这是因为中晚期导电薄板的集流效应产生的附加垂直异常磁场在空间方向与背景异常相互消长,导致异常出现加强与削弱,甚至正负相反的现象。
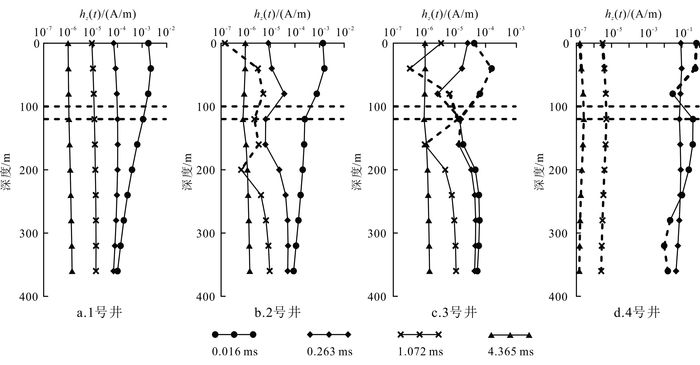
|
| 水平虚线为异常体的上下界面位置,垂直磁场响应虚线表示为负值。 图 9 不同井位垂直磁场响应随深度变化的曲线 Figure 9 Curves of hz(t) with respect to depth in different wells |
|
|
本文通过对赫姆霍兹方程进行有限差分离散,借助MUMPS数学软件包和余弦变换技术,完成了地-井瞬变电磁三维正演,并研究了低阻薄板异常体地-井瞬变电磁特征。通过数值模拟,得到以下结论:
1) 本文以矩形大定源回线为例,提出的结合频率域三维正演和余弦变换技术计算水平地形条件下三维瞬变电磁响应的模拟方案是可行的。
2) 在模拟过程中,采用虚框等效叠加方法计算背景介质格林函数,使发射可位于任意层位,计算点可扩展到发射回线边界外的三维空间任意位置,实现了全空间三维瞬变电磁响应的计算。
3) 模拟结果验证了矩形发射回线源激发的场以“烟圈”的形式不断向下扩散,随着时间衰减,“烟圈”的范围扩大,强度减弱;低阻异常体对电磁场有“吸附”性质,低阻体产生的电磁场随着时间延迟衰减较慢。
4) 导电围岩中水平薄板模型模拟结果表明,井孔的瞬变响应受观测位置影响较大,特别是异常体边缘和异常体内部,电压剖面曲线在异常体位置附近变化较大,且中期时间道响应可能会出现变号现象。
在没有实现地-井瞬变电磁三维反演前,本文的研究工作可以为地-井瞬变电磁数据的采集与解释提供一个技术支持,进一步为地-井瞬变电磁数据反演奠定理论基础。
| [1] |
蒋邦远.
实用近区磁源瞬变电磁法勘探[M]. 北京: 地质出版社, 1998.
Jiang Bangyuan. Applied near Zone Magnetic Source Transient Electromagnetic Exploration[M]. Beijing: Geological Publishing House, 1998. |
| [2] |
牛之琏.
时间域电磁法原理[M]. 长沙: 中南大学出版社, 2007.
Niu Zhilian. Theory of Time Domain Electromagentic Method[M]. Changsha: Central South University of Technology Press, 2007. |
| [3] | Dyck A V, West G F. The Role of Simple Computer Models in Interpretations of Wide-Band, Drill-Hole Electromagnetic Surveys in Mineral Exploration[J]. Geophysics, 1984, 49(7): 957-980. DOI:10.1190/1.1441741 |
| [4] | Swidinsky A, Nabighian M. On Smoke Rings Produ-ced by a Loop Buried in a Conductive Half-Space[J]. Geophysics, 2015, 80(4): E225-E236. DOI:10.1190/geo2015-0002.1 |
| [5] | Nabighian M N. Quasi-Static Transient Response of a Conducting Half-Space:An Approximate Representation[J]. Geophysics, 1979, 44(10): 1700-1705. DOI:10.1190/1.1440931 |
| [6] | West R C, Ward S H. The Borehole Transient Elec-tromagnetic Response of a Three-Dimensional Fracture Zone in a Conductive Half-Space[J]. Geophysics, 1988, 53(11): 1469-1478. DOI:10.1190/1.1442427 |
| [7] |
李建慧, 刘树才, 焦险峰, 等. 地-井瞬变电磁法三维正演研究[J].
石油地球物理勘探, 2015, 50(3): 556-564.
Li Jianhui, Liu Shucai, Jiao Xianfeng, et al. Three-Dimensional Forward Modeling for Surface-Borehole Transient Electromagnetic Model[J]. Oil Geophysical Prospecting, 2015, 50(3): 556-564. |
| [8] |
徐正玉, 杨海燕, 邓居智, 等. 基于异常场的地-井瞬变电磁法正演研究[J].
物探与化探, 2015, 39(6): 1176-1182.
Xu Zhengyu, Yang Haiyan, Deng Juzhi, et al. Research on Forward Simulation of Down-Hole TEM Based on the Abnormal Filed[J]. Geophysical and Geochemical Exploration, 2015, 39(6): 1176-1182. |
| [9] |
杨海燕, 岳建华. 巷道影响下三维全空间瞬变电磁法响应特征[J].
吉林大学学报(地球科学版), 2008, 38(1): 129-134.
Yang Haiyan, Yue Jianhua. Response of Characteristics of the 3D Whole-Space TEM Disturbed by Roadway[J]. Journal of Jilin University (Earth Science Edition), 2008, 38(1): 129-134. |
| [10] |
杨海燕, 徐正玉, 岳建华, 等. 覆盖层下三维板状体地-井瞬变电磁响应[J].
物探与化探, 2016, 40(1): 190-196.
Yang Haiyan, Xu Zhengyu, Yue Jianhua, et al. 3D Inclined Conductor Behavior of Down-Hole Transient Electromagnetic Method with Overburden Layer[J]. Geophysical and Geochemical Exploration, 2016, 40(1): 190-196. |
| [11] |
杨海燕, 邓居智, 汤洪志, 等. 全空间瞬变电磁法资料解释方法中的平移算法[J].
吉林大学学报(地球科学版), 2014, 44(3): 1012-1017.
Yang Haiyan, Deng Juzhi, Tang Hongzhi, et al. Translation Algorithm of Data Interpretation Technique in Full-Space Transient Electromagnetic Method[J]. Journal of Jilin University (Earth Science Edition), 2014, 44(3): 1012-1017. |
| [12] |
翁爱华, 刘云鹤, 贾定宇, 等. 地面可控源频率测深三维非线性共轭梯度反演[J].
地球物理学报, 2012, 55(10): 3506-3515.
Weng Aihua, Liu Yunhe, Jia Dingyu, et al. Three-Dimensional Controlled Source Electromagnetic Inversion Using Non-Linear Conjugate Gradient[J]. Chinese Journal of Geophysics, 2012, 55(10): 3506-3515. DOI:10.6038/j.issn.0001-5733.2012.10.034 |
| [13] |
贲放, 刘云鹤, 黄威, 等. 各向异性介质中的浅海海洋可控源电磁响应特征[J].
吉林大学学报(地球科学版), 2016, 46(2): 581-593.
Ben Fang, Liu Yunhe, Huang Wei, et al. MCSEM Responses for Anisotropic Media in Shallow Water[J]. Journal of Jilin University (Earth Science Edition), 2016, 46(2): 581-593. |
| [14] | Alumbaugh D L, Newman G A, Prevost L, et al. Three-Dimensional Wideband Electromagnetic Modeling on Massively Parallel Computers[J]. Radio Science, 1996, 31(1): 1-23. DOI:10.1029/95RS02815 |
| [15] | Yee K S. Numerical Solution of Initial Value Prob-lems of Maxwells Equations in Isotropic Media[J]. IEEE Transactions on Antennas and Propagation, 1966(AP-14): 302-307. |
| [16] | Sasaki Y, Yi M J, Choi J, et al. Frequency and Time Domain Three-Dimensional Inversion of Electromagnetic Data for a Grounded-Wire Source[J]. Journal of Applied Geophysics, 2015, 112: 106-114. DOI:10.1016/j.jappgeo.2014.09.016 |
| [17] | Kelbert A, Meqbel N, Egbert G D, et al. ModEM:A Modular System for Inversion of Electromagnetic Geophysical Data[J]. Computers & Geosciences, 2014, 66: 40-53. |
| [18] | Egbert G D, Kelbert A. Computational Recipes for Electromagnetic Inverse Problems[J]. Geophysical Journal International, 2012, 189(1): 251-267. DOI:10.1111/gji.2012.189.issue-1 |
| [19] | Mackie R L, Smith J T, Madden T R. Three-Di-mensional Electromagnetic Modeling Using Finite Difference Equations:The Magnetotelluric Example[J]. Radio Science, 1994, 29(4): 923-935. DOI:10.1029/94RS00326 |
| [20] | Oldenburg D W, Haber E, Shekhtman R. Three Di-mensional Inversion of Multisource Time Domain Electromagnetic Data[J]. Geophysics, 2013, 78(1): E47-E57. DOI:10.1190/geo2012-0131.1 |
| [21] | Weng A H, Liu Y H, Chen Y L, et al. Computation of Transient Electromagnetic Field from a Rectangular Loop over Stratified Earths[J]. Chinese Journal of Geophysics, 2010, 53(3): 646-650. |
| [22] | Weng A H, Liu Y H, Yin C C, et al. Singularity-Free Green's Function for EM Sources Embedded in a Stratified Medium[J]. Applied Geophysics, 2016, 13(1): 25-36. DOI:10.1007/s11770-016-0549-x |
| [23] |
张成范, 翁爱华, 孙世栋, 等. 计算矩形大定源回线瞬变电磁测深全区视电阻率[J].
吉林大学学报(地球科学版), 2009, 39(4): 755-758.
Zhang Chengfan, Weng Aihua, Sun Shidong, et al. Computation of Whole-Time Apparent Resistivity of Large RectangularLoop[J]. Journal of Jilin University (Earth Science Edition), 2009, 39(4): 755-758. |
| [24] |
李建平, 李桐林, 张辉, 等. 不规则回线源层状介质瞬变电磁场正反演研究及应用[J].
吉林大学学报(地球科学版), 2005, 35(6): 790-795.
Li Jianping, Li Tonglin, Zhang Hui, et al. Study and Application of the TEM Forward and Inversion Problem of Irregular Loop Source over the Layered Medium[J]. Journal of Jilin University (Earth Science Edition), 2005, 35(6): 790-795. |
| [25] | Das U C, de Hoop A T. Efficient Computation of Apparent Resistivity Curves for Depth Profiling of a Layered Earth[J]. Geophysics, 1995, 60(6): 1691-1697. DOI:10.1190/1.1443901 |
| [26] | Chave A D. Numerical Integration of Related Hankel Transforms by Quadrature and Continued Fraction Expansion[J]. Geophysics, 1983, 48(12): 1671-1686. DOI:10.1190/1.1441448 |
| [27] | Newman G A, Hohmann G W. Transient Electro-magnetic Responses of High-Contrast Prisms in a Layered Earth[J]. Geophysics, 1988, 53(5): 691-706. DOI:10.1190/1.1442503 |