2. 国防科学技术大学机电工程与自动化学院, 长沙 410000;
3. 浙江大学地球科学学院, 杭州 310000;
4. 武警黄金部队第二支队, 呼和浩特 010000
2. College of Mechatronic Engineering and Automation, National University of Defense Technology, Changsha 410000, China;
3. School of Earth Sciences, Zhejiang University, Hangzhou 310000, China;
4. Second Gold detachment, The Chinese Armed Police Force, Hohhot 010000, China
0 引言
重力场向下延拓是一种重要的数据处理和解释手段[1]。它将异常观测值下延至不同高度,为后续数据分析做准备,能够突出浅部、局部的地质体特征。另外,在重力场辅助导航中,重力数据是无源导航的重要研究内容[2-3],而向下延拓为构建空间重力数据库提供了主要途径。向下延拓的方法有很多种,常用方法有空间域插值下延法[4]、傅里叶变换(FFT)下延法[5]和积分迭代下延法[6-7]等。虽然相对于空间域插值下延法,FFT下延法的计算更简便、速度更快,但由于重力场向下延拓是典型的不适定问题、频率域下延因子具有放大高频成分和数据噪声的效应、傅里叶变换离散过程和截断误差引起的延拓结果振荡等原因,FFT下延法的结果并不稳定,且下延深度较浅,一般只能下延2~3倍点距。为得到稳定的下延结果,不同学者发展了不同的FFT下延法改进方法,如正则化方法[8]、维纳滤波法[9]、匹配滤波法[10-11]等。虽然,这些改进方法使下延稳定性得到了一定提高,但随着向下延拓深度的增大,这些改进方法的下延深度仍不能超过3~5倍点距。相对于FFT下延法,积分迭代下延法能够较好地解决重力场向下延拓的不稳定性,且实现了大点距向下延拓(10~20点距);但其计算需要多次迭代,对噪声产生多次迭代累加,导致计算效率和精度降低[12]。
针对重力场向下延拓的不稳定性等问题,本文基于求解常微分方程的多步思想进行向下延拓,利用Adams-Bashforth公式,引入向上延拓至不同高度的垂向一阶导数,提出空间域重力场向下延拓三阶Adams-Bashforth公式法。然后比较FFT下延法、积分迭代下延法和三阶Adams-Bashforth公式下延法在模型数据应用中的差异,分析这3种下延方法所得结果与真实值的均方误差随下延深度的变化曲线。最后将本文新提出的下延方法应用于实际数据,以验证方法的稳定性和准确性。
1 基本原理 1.1 空间域插值下延法、FFT下延法和积分迭代下延法 1.1.1 空间域插值下延法重力场向下延拓是求观测高度以下、指向场源方向某一深度的重力场。不同高度的重力场之间的关系[13]表述如下:
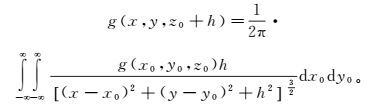 (1)
(1) 式中:g (x0, y0, z0)表示观测面的重力场;h为地下距观测面的深度,即下延深度;g (x, y, z0+h)表示观测平面以下、场源以上某一深度的重力场;(x0, y0, z0)为观测面坐标;(x, y)为延拓后平面的水平坐标。
向下延拓问题可视为求积分问题,采用不同积分求取方法可以得到不同形式的延拓方法。然而,下延边界值有微小变化时,所得下延结果可以产生很大变化,即下延是不稳定的;所以在空间域进行向下延拓一般采用近似方法,常用方法有多项式插值法、级数正则化法和调和分析法等。以复数拉格朗日插值多项式近似计算重力场向下延拓为例,假设测点间距和单位延拓深度均为单位1。其一般形式为[14]
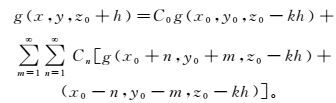 (2)
(2) 式中:Cn(n=0, 1, 2,…)为向下延拓系数;n, m分别为平面坐标x0、y0上的插值点数;k为插值多项式阶数;-kh为向上延拓距离。
1.1.2 FFT下延法一般插值形式下延公式存在计算量大和精度低的问题,自从傅里叶变换引入地球物理解释后,因其表达式简单、计算速度快,经傅里叶变换得到的波数域下延公式法逐渐成为主流方法。在空间域,公式(1) 为褶积形式。由于空间域的褶积经过傅里叶变换可变为乘积,所以,对式(1) 两边做傅里叶变换,得到波数域的向下延拓公式:
 (3)
(3) 式中:G (u0, v0, z0+h)为g (x0, y0, z0+h)的二维傅里叶变换;G (u0, v0, z0)为g (x0, y0, z0)的二维傅里叶变换;(u2+v2)1/2为波数。然后,对公式(3) 左侧的G (u, v, z0+h)进行傅里叶逆变换。此即FFT下延法。
1.1.3 积分迭代下延法由于波数域向下延拓因子e2π(u2+v2)1/2h具有放大效应,直接利用FFT下延法进行重力场向下延拓对含有高频信息或者噪声的数据计算不稳定,延拓2~3个测点距深度后,结果发散。徐世浙[6]提出积分迭代下延法,该方法可将下延深度提高到10~20倍点距。积分迭代下延法下延步骤如下。
设面ΓB上的重力异常gB是已知的,距其下h深的面ΓA上的异常gA是未知待求的,ΓB、ΓA间无场源。首先,将ΓB上的重力异常垂直等价于gB的对应点上,作为ΓA上的初值gA1。其次,从gA的初值gA1,利用频率域向上延拓公式,得到面ΓB上第一次迭代的计算值gB1:
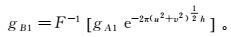 (4)
(4) 式中,F-1为傅里叶逆变换符。进而计算ΓB上的重力异常。也可以使用其他上延方法计算。再次,根据ΓB上的原始重力值gB和上延计算重力值gB1的差值对ΓA上的重力异常gA进行校正。最后,反复迭代上述过程,直到观测高度上的实测值与计算值的差值小于一个很小的常量,完成下延迭代计算。一般迭代次数为20~50次。
但是,由于积分迭代下延法需要进行反复迭代,计算效率不高,同时也会使噪声累加,因此本文提出基于Adams-Bashforth公式的重力场向下延拓方法。
1.2 基于Adams-Bashforth公式的下延法在地表上半空间,重力场满足调和函数性质,可以用某一平面重力值计算该空间其他平面(或者点)的数据值,实现由重力场平面值到其垂向空间值的换算,即重力解析延拓。但是,由于地面下半空间的重力场不满足调和函数性质,则由实测值向地表下换算时解不稳定,是不适定问题,即向下延拓结果不稳定。另外,由于重力场求解区域有限,公式(1) 积分域为无穷,对重力场做延拓时,需利用有限平面数据数值积分近似替代无限积分。因此,本文基于更广泛适用的物理数学条件,推导了新的向下延拓方法Adams-Bashforth公式下延法。
首先,在物理上,重力场不仅是横向连续变化的,还具有垂向连续变化性质[15];其次,在数学上,重力场存在横向和垂向导数,即使不具有调和函数性质,仍然满足微分定理。因此,对重力场的垂直方向做偏导数,即对z进行差商,可得到重力场的微分形式:
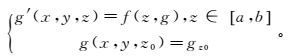 (5)
(5) 式中:g′(x, y, z)为重力场的垂向一阶导数;f (z, g)为g和z的函数关系式;gz0为下延前的重力值。通过数值积分法与待定系数法,得到等式(5) 的多步法公式解,一般表现形式[16-17]为
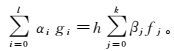 (6)
(6) 式中:gi为不同高度的重力场值;fj为不同高度重力场的垂向一阶导数;l为重力场高度间隔数;k为重力场垂向一阶导数高度间隔数;αi,βj为多步线性解的系数,是常数,且αi=1,|α0|+|β0|≠0。当βk=0时,式(6) 为显式方法;当βk≠0时,式(6) 为隐式方法。只要给定k,确定对αi、βj的要求,就可以通过解线性方程组求出αi、βj,构造相应的多步法公式。所以,根据常微分方程数值解法的有效方法之一[18-19]——线性多步法的显式Adams-Bashforth公式,得到向下延拓公式(1) 的表达为
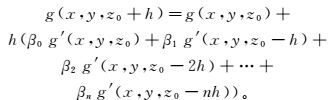 (7)
(7) 式中:β0, β1, β2, …, βn的取值可以参考数值计算公式系数表[16];g′(x, y, z0), g′(x, y, z0-h), …, g′(x, y, z0-nh)分别为高度z0, z0-h, …, z0-nh上重力场的垂向一阶导数。
一般情况下,已知观测面上的重力异常场,可以直接测得或者通过计算获得重力异常垂向导数。重力异常垂向导数向上延拓稳定且收敛,则不同高度的重力垂向一阶导数为
 (8)
(8) 式中:G′(u, v, z0)是z0高度频率域重力异常垂向导数;G′(u, v, z0-kh)是上延kh高度后频率域重力异常垂向导数。
利用式(8) 计算的不同高度重力垂向一阶导数,结合式(7) 的数值计算结果即可得到基于Adams-Bashforth法重力场向下延拓公式。实际应用时,需选有限阶进行计算。为便于说明,本文选择三阶显式Adams-Bashforth公式。重力场向下延拓三阶Adams-Bashforth公式法近似表达式为
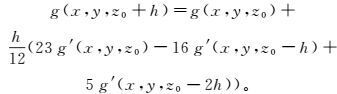 (9)
(9) 一般情况下,无论是空间域还是频率域,向下延拓前均需要进行扩边处理,以防止延拓结果出现边界效应。但是,扩边方法种类繁多,对于不同数据类型,不同扩边方法对延拓结果影响较大,额外引入扩边方法不利于比较延拓方法本身的好坏。同时,一般下延过程均伴随滤波处理,滤波方法及滤波参数的选择对下延结果有直接影响。因此,为突出延拓方法本身的优缺点,本文所涉及下延方法均不进行任何扩边和滤波处理。
2 模型试验为说明本文方法效果,在模型试验中给出本文三阶Adams-Bashforth下延法与经典FFT下延法以及由徐世浙[6]提出的、经过多位学者验证的[2, 20-22]、目前较新且较权威的积分迭代下延法结果的比较。
理论模型(图 1)由两个顶底界面埋深不同、大小不一的长方体组合而成:长方体1(红色标记)x、y和z方向边长分别为10、20、20 m,中心点坐标为(60, 80, -23),顶界面距地面13 m,底界面距地面33 m;长方体2(蓝色标记)x、y和z方向边长分别为40、10、20 m,中心点坐标为(60, 50, -25),顶界面距地面为15 m,底界面距地面35 m。两个长方体密度相同,与围岩密度差均为0.9 kg/m3。地面测网共计130条测线,每条测线130个测点,网格间距为1 m。

|
| 图 1 地下模型空间分布 Figure 1 Position of underground rectangular model |
|
|
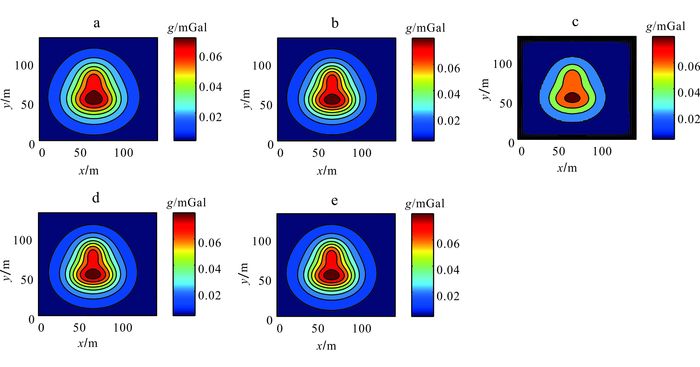
首先将距离地面0 m、不含噪声的理论重力异常(图 2a)向下延拓2 m,结果如图 2b所示。所用垂向一阶导数为理论值,非换算获得;将垂向梯度异常上延至不同高度得到不同高度的垂向一阶导数值。积分迭代下延法迭代步长为1,收敛误差为0.000 1 mGal (模型数据的精度也为0.000 1 mGal),迭代43次。由图 2可知,在均未扩边的情况下,向下延拓2 m时:对比下延2倍点距的理论异常值(图 2b),本文Adams-Bashforth下延法结果(图 2e)更加准确;相对于FFT下延法(图 2c),本文Adams-Bashforth下延法边界损失小;积分迭代下延法(图 2d)和本文Adams-Bashforth下延法的结果均稳定且收敛,相对于理论下延值,两种方法都能给出准确的下延异常。
|
| a.地面理论计算重力异常;b.向下2 m理论计算重力异常;c. FFT法下延2 m结果;d.积分迭代法下延2 m结果;e.本文方法下延2 m结果。 图 2 不含噪声向下延拓2 m结果 Figure 2 Downward continuation results by 2 m without noises |
|
|
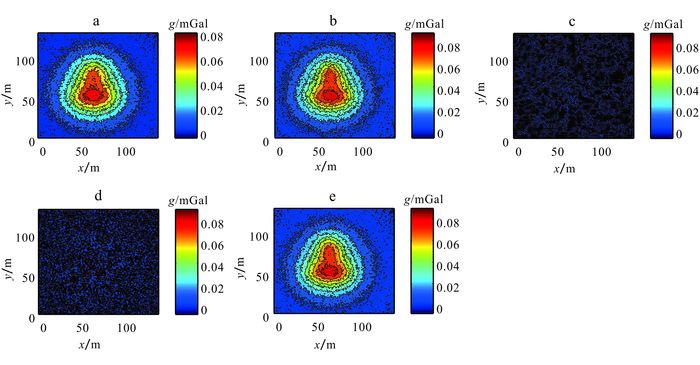
对距离地面0 m、含5%随机白噪声的理论重力异常值(图 3a)向下延拓2 m,得到延拓结果(图 3b)。所用垂向一阶导数为含有噪声的理论值,非换算获得;将垂向梯度异常上延至不同高度得到不同高度的垂向一阶导数值。积分迭代下延法迭代步长为1,收敛误差为0.000 1 mGal,迭代50次(建议最大次数)。由图 3可知,在未进行扩边、正则化及其他滤波去噪处理情况下,向下延拓2 m时:对比下延2倍点距的理论含噪异常值(图 3b),本文Adams-Bashforth下延法结果(图 3e)更加准确;相对FFT下延法(图 3c)和积分迭代下延法(图 3d),本文Adams-Bashforth下延法的下延过程稳定且收敛。
|
| a.地面理论计算重力异常;b.向下2 m理论计算重力异常;c. FFT法下延2 m结果;d.积分迭代法下延2 m结果;e.本文方法下延2 m结果。 图 3 含5%噪声向下延拓2 m结果 Figure 3 Downward continuation results by 2 m with 5% white noises |
|
|
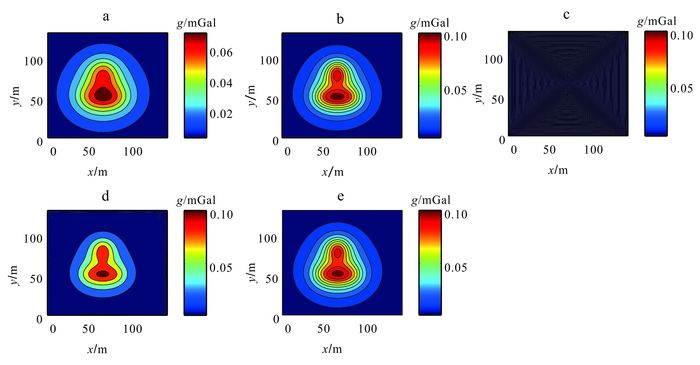
再将距离地面0 m、不含噪声的理论重力异常(图 4a)向下延拓5 m,结果如图 4b所示。所用垂向一阶导数依然为理论值;依然将其上延至不同高度得到不同高度的垂向一阶导数值。积分迭代下延法迭代步长为1,收敛误差为0.000 1 mGal (模型数据的精度也为0.000 1 mGal),迭代50次。由图 4可知,在均未扩边的情况下,向下延拓5 m时:对比下延5倍点距的理论异常值(图 4b),本文Adams-Bashforth下延法结果(图 4e)更加准确;相对于FFT下延法(图 4c),本文Adams-Bashforth下延法收敛;相对积分迭代下延法(图 4d),本文Adams-Bashforth下延法的结果边界损失小。
|
| a.地面理论计算重力异常;b.向下5 m理论计算重力异常;c. FFT法下延5 m结果;d.积分迭代法下延5 m结果;e.本文方法下延5 m结果。 图 4 不含噪声向下延拓5 m结果 Figure 4 Downward continuation results by 5 m without noises |
|
|
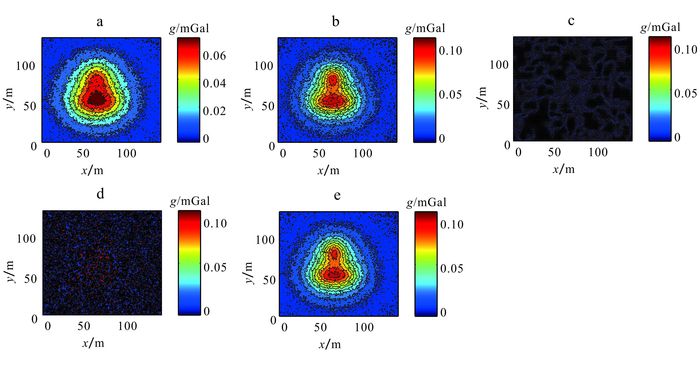
最后对距离地面0 m、含5%随机白噪声的理论重力异常值(图 5a)向下延拓5 m,得到延拓结果(图 5b)。所用垂向一阶导数为含有噪声的理论值,非换算获得;将垂向梯度异常上延至不同高度得到不同高度的垂向一阶导数值。积分迭代下延法迭代步长为1,收敛误差为0.000 1 mGal,迭代50次(建议最大次数)。在未进行扩边、正则化及其他滤波去噪处理情况下,由图 5可知,FFT下延法(图 5c)和积分迭代下延法(图 5d)严重发散,而本文Adams-Bashforth下延法过程(图 5e)稳定收敛且具有很好抗噪能力。
|
| a.地面理论计算重力异常;b.向下5 m理论计算重力异常;c. FFT法下延5 m结果;d积分迭代法下延5 m结果;e.本文方法下延5 m结果。 图 5 含5%噪声向下延拓5 m结果 Figure 5 Downward continuation results by 5 m with 5% white noises |
|
|
图 6给出了无噪声数据FFT下延法、积分迭代下延法、本文Adams-Bashforth下延法计算结果与真实值均方误差随下延点距的对数函数变化曲线。通过对比可知:向下延拓相同点距时,FFT下延法的均方误差随下延深度增加指数增大,而本文Adams-Bashforth下延法的均方误差小很多(图 6a);同时,本文Adams-Bashforth下延法的均方误差小于积分迭代下延法(图 6b)。均方误差曲线说明本文Adams-Bashforth下延法的结果更准确,更接近真实异常值。

|
| 图 6 本文Adams-Bashforth下延法与FFT下延法(a)、积分迭代下延法(b)计算结果与真实结果均方误差比较 Figure 6 Comparison of the RMS between the real value and the downward continuation results of this Adams-Bashforth method with the FFT method (a) and with the integral-iteration method (b) |
|
|
为验证本文提出Adams-Bashforth下延法的实际效果,对加拿大某地区实测航空重力数据进行向下延拓。该重力资料网格间距为400 m,航空布格重力异常(图 7a)以及垂向一阶导数均为实测资料。将实测航空布格重力异常向上延拓2 000 m,作为上部已知重力异常(图 7b)。将2 000 m高度重力异常(图 7b)的垂向一阶导数再分别向上延拓至4 000 m和6 000 m,利用本文三阶Adams-Bashforth下延法对图 7b向下延拓2 000 m,得到结果如图 7c所示。对比真实重力异常(图 7a)和本文方法下延的重力异常(图 7c)可以看出,本文延拓结果与实测重力异常吻合,能够很好地恢复下延场中的微小异常信息,得到相对准确的下延结果。延拓后结果与原始异常的相对误差如图 7d所示;通过计算,延拓后结果与原始异常的均方误差为1.986 mGal。由此可知,本文的三阶Adams-Bashforth下延法计算结果与真实值之间误差小、边界效应不明显、计算稳定且收敛。

|
| a.实测布格重力异常;b.向上延拓5倍点距结果;c.由b下延5倍点距结果;d.下延结果c与原始异常a的误差。 图 7 实测航空重力异常向下延拓5倍点距结果 Figure 7 Downward continuation results of the real measured airborne gravity anomalies with 5 interval |
|
|
本文基于求解常微分方程的Adams-Bashforth公式实现了重力场向下延拓,且对比了FFT下延法、积分迭代下延法和本文方法对不同下延深度的效果,通过模型和实际数据的计算可以得到如下结论:
1) 对模型分别下延2倍点距和5倍点距以及对实际数据下延5倍点距,三阶Adams-Bashforth公式下延法能够获得较深且准确的重力场向下延拓结果。
2) 与FFT下延法和积分迭代下延法相比,三阶Adams-Bashforth公式下延法的计算更稳定、抗噪能力更强。
3) 在三阶Adams-Bashforth公式下延法中,需使用重力异常垂向一阶导数,但是目前国内没有实测重力垂向梯度数据,本文使用实测值;所以仍需研究并解决计算垂向梯度和实测垂向梯度对本文方法的影响。
4) 三阶Adams-Bashforth公式下延法可有效应用于实际数据向下延拓处理,对识别重力场的“浅部”和“局部”特征以及重建重力数据进行辅助导航等具有十分重要的意义。
5) 本文涉及重力垂向导数的使用,所以值得进一步研究测量垂向导数的重力梯度仪。
致谢: Geosoft公司提供了实测航空重力数据,孙勇博士在笔者工作中提供了帮助,在此一并表示感谢。| [1] |
高玉文, 骆遥, 文武. 补偿向下延拓方法研究及应用[J].
地球物理学报, 2012, 55(8): 2747-2756.
Gao Yuwen, Luo Yao, Wen Wu. The Compensation Method for Downward Continuation of Potential Field from Horizontal Plane and Its Application[J]. Chinese Journal of Geophysics, 2012, 55(8): 2747-2756. DOI:10.6038/j.issn.0001-5733.2012.08.026 |
| [2] |
张辉, 陈龙伟, 任治新, 等. 位场向下延拓迭代法收敛性分析及稳健向下延拓方法研究[J].
地球物理学报, 2009, 52(2): 511-518.
Zhang Hui, Chen Longwei, Ren Zhixin, et al. Analysis on Convergence of Iteration Method for Potential Fields Downward Continuation and Research on Robust Downward Continuation Method[J]. Chinese Journal of Geophysics, 2009, 52(2): 511-518. |
| [3] |
张志厚, 吴乐园. 位场向下延拓的相关系数法[J].
吉林大学学报(地球科学版), 2012, 42(6): 1912-1919.
Zhang Zhihou, Wu Leyuan. Correlation Coefficient Method for Downward Continuation of Potential Fields[J]. Journal of Jilin University (Earth Science Edition), 2012, 42(6): 1912-1919. |
| [4] | Peters L J. The Direct Approach to Magnetic Inter-pretation and Its Practical Application[J]. Geophysics, 1949, 14(3): 290. DOI:10.1190/1.1437537 |
| [5] | Dean W C. Frequency Analysis for Gravity and Mag-netic Interpretation[J]. Geophysics, 2002, 23(1): 97. |
| [6] |
徐世浙. 位场延拓的积分-迭代法[J].
地球物理学报, 2006, 49(4): 1054-1060.
Xu Shizhe. The Integral-Iteration Method for Continuation of Potential Fields[J]. Chinese Journal of Geophysics, 2006, 49(4): 1054-1060. |
| [7] |
于德武, 龚胜平. 对迭代法位场向下延拓方法的剖析[J].
吉林大学学报(地球科学版), 2015, 45(3): 934-940.
Yu Dewu, Gong Shengping. Analysis of the Potential Field Downward Continuation Iteration Method[J]. Journal of Jilin University (Earth Science Edition), 2015, 45(3): 934-940. |
| [8] | Tikhonov A N, Glasko V B, Litvinenko O K, et al. Analytic Continuation of a Potential in the Direction of Disturbing Masses by the Regularization Method[J]. Izv Earth Physics, 1968, 12: 30-48. |
| [9] | Clarke G K C. Optimum Second-Derivative and Down-ward-Continuation Filters[J]. Geophysics, 2012, 34(3): 424. |
| [10] | Pawlowski R S. Preferential Continuation for Poten-tial-Field Anomaly Enhancement[J]. Geophysics, 1995, 60(2): 390-398. DOI:10.1190/1.1443775 |
| [11] |
王彦国, 王祝文, 张凤旭, 等. 位场向下延拓的导数迭代法[J].
吉林大学学报(地球科学版), 2012, 42(1): 240-245.
Wang Yanguo, Wang Zhuwen, Zhang Fengxu, et al. Derivative-Iteration Method for Downward Continuation of Potential Fields[J]. Journal of Jilin University (Earth Science Edition), 2012, 42(1): 240-245. |
| [12] |
陈生昌, 肖鹏飞. 位场向下延拓的波数域广义逆算法[J].
地球物理学报, 2007, 50(6): 1571-1579.
Chen Shengchang, Xiao Pengfei. Wavenumber Domain Generalized Inverse Algorithm for Potential Field Downward Continuation[J]. Chinese Journal of Geophysics, 2007, 50(6): 1571-1579. |
| [13] | Blakely R J. Potential Theory in Gravity and Mag-netic Applications[M]. Cambridge: Cambridge University Press, 2003. |
| [14] |
曾华霖.
重力场与重力勘探[M]. 北京: 地质出版社, 2005.
Zeng Hualin. Gravity Field and Gravity Exploration[M]. Beijing: Geological Publishing House, 2005. |
| [15] | Fedi M, Florio G. A Stable Downward Continuation by Using the ISVD Method[J]. Geophysical Journal International, 2002, 151(1): 146-156. DOI:10.1046/j.1365-246X.2002.01767.x |
| [16] | Fornberg B. Calculation of Weights in Finite Diffe-rence Formulas[J]. Siam Review, 2002, 40(3): 685-691. |
| [17] |
刘冬兵. 四阶Adams-Bashforth组合公式的预估-校正方法的对比试验[J].
西昌学院学报(自然科学版), 2012, 26(3): 43-46.
Liu Dongbing. The Comparative Test of Fourth Order Adams-Bashforth Combination Formula Predictor-Corrector Methods[J]. Journal of Xichang College (Natural Science Edition), 2012, 26(3): 43-46. |
| [18] |
王新民, 朱洪亮.
工程数据:计算方法[M]. 北京: 高等教育出版社, 2005.
Wang Xinmin, Zhu Hongliang. Engineering Mathematics:Numerical Methods[M]. Beijing: Higher Education Press, 2005. |
| [19] | Butcher J C. Numerical Methods for Ordinary Diffe-rential Equations[M]. Hoboken: Wiley, 2008. |
| [20] |
刘东甲, 洪天求, 贾志海, 等. 位场向下延拓的波数域迭代法及其收敛性[J].
地球物理学报, 2009, 52(6): 1599-1605.
Liu Dongjia, Hong Tianqiu, Jia Zhihai, et al. Wave Number Domain Iteration Method for Downward Continuation of Potential Fields and Its Convergence[J]. Chinese Journal of Geophysics, 2009, 52(6): 1599-1605. |
| [21] |
于波, 翟国君, 刘雁春, 等. 噪声对磁场向下延拓迭代法的计算误差影响分析[J].
地球物理学报, 2009, 52(8): 2182-2188.
Yu Bo, Zhai Guojun, Liu Yanchun, et al. Analysis of Noise Effect on the Calculation Error of Downward Continuation with Iteration Method[J]. Chinese Journal of Geophysics, 2009, 52(8): 2182-2188. |
| [22] |
姚长利, 李宏伟, 郑元满, 等. 重磁位场转换计算中迭代法的综合分析与研究[J].
地球物理学报, 2012, 55(6): 2062-2078.
Yao Changli, Li Hongwei, Zheng Yuanman, et al. Research on Iteration Method Using in Potential Field Transformations[J]. Chinese Journal of Geophysics, 2012, 55(6): 2062-2078. DOI:10.6038/j.issn.0001-5733.2012.06.028 |


