0 引言
在低阻泥浆条件下,侧向测井在高阻地层评价过程中发挥着至关重要的作用。1972年,Suau等[1]提出了双侧向测井仪。随后,国外相继开发出具有较高分辨率或具备方位电阻率测量的双侧向和阵列侧向测井仪器[2-6]。近年来,国内也相继研制出高分辨率的双侧向和阵列侧向测井仪[7-9],以及具有方位探测能力的侧向测井仪器[10-11]。侧向测井电极系主要由主电极、屏蔽电极、监督电极和返回电极等构成,相邻电极间绝缘连接。各电极结构及间隔尺寸决定了仪器的探测特性。为了优化电极结构设计,有必要分析电极结构对探测特性的影响。现公开发表的文献中,一般都是直接给出电极系结构,而很少研究电极系结构对测井响应的影响。另外,侧向测井仪器一般采用基于电路调节的硬件聚焦方式,监督电极残余电位差大小严重影响测量结果的准确性[3, 12]。而且,阵列侧向测井[4-6, 9, 11]一般利用增加电极数量来实现阵列化测量,电极数量繁多,电路复杂。
笔者提出了一种基于电位场叠加原理的软件聚焦方法[3, 13-14],使监督电极电位差严格为0,以提高测量结果的准确性。本文利用有限元数值模拟方法[15]系统分析了常见侧向测井电极系结构对电极系数、井眼影响、径向探测深度等测井响应的影响;通过对比硬件聚焦中监督电极残余电位差对测井响应的影响,引入聚焦系数,利用软件聚焦原理实现双侧向测井的阵列化测量方法,以期为今后侧向测井电极设计和聚焦方法提供理论依据。
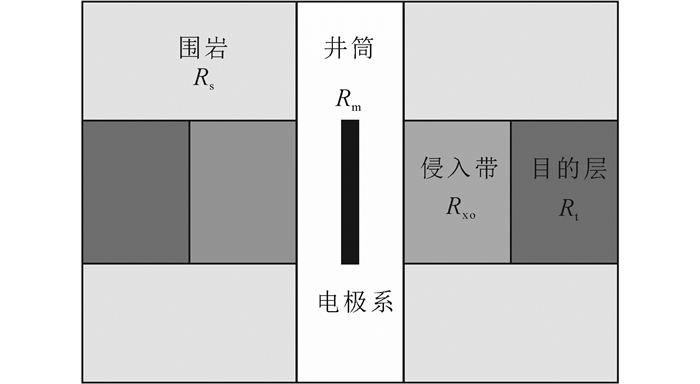
1 数值模拟基础双侧向及阵列侧向测井可以简化为如图 1所示的二维模型,电位场分布满足轴对称微分方程。在电阻率为ρ的区域中,柱坐标系(r, φ, z)电位函数U(r, z)满足
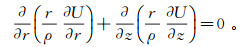 (1)
(1) 式(1)满足远端第一类边界条件:
 (2)
(2) 在电极系表面的绝缘环及对称轴边界满足第二类边界条件:
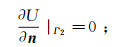 (3)
(3) 在电极表面满足等位面边界条件:
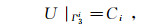 (4)
(4)  (5)
(5) 在地层交界面满足连续边界条件:
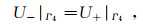 (6)
(6) 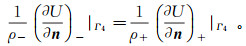 (7)
(7) 式(2)-(7)中:Γ1表示远端边界;Γ2表示电极系表面绝缘边界和对称轴边界;Γ3i表示第i个电极表面边界;Γ4表示地层不同区域连续边界;Ci表示待定常数值;Ii表示第i个电极电流;n表示交界面法向单位向量;“-”、“+”表示交界面两侧。
|
| Rm为泥浆电阻率;Rxo为侵入带电阻率;Rt为目的层电阻率;Rs为围岩电阻率。 图 1 侧向测井二维数值模拟模型 Figure 1 2D numerical simulation model for laterolog |
|
|
利用变分原理将上述微分方程的边值问题转化为电位U的变分,二维变分为
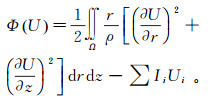 (8)
(8) 式中:Ii、Ui分别表示第i个电极的电流和电位;Ω为积分区域。侧向测井的探测特性主要包括径向探测深度、纵向分辨率及井眼影响等。本文即利用有限元方法求解上述变分问题,进而求解视电阻率,分析侧向测井电极系结构、聚焦方法对测井响应的影响。
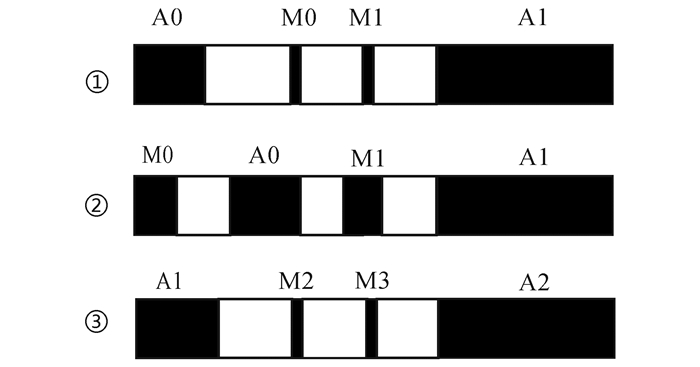
2 电极系结构对探测特性的影响 2.1 侧向测井常见的电极系结构图 2给出了侧向测井中经常采用的三种电极系结构(对称部分未画出)。图 2中,A0为主电极,M0、M1、M2、M3为监督电极,A1、A2为屏蔽电极,各电极之间为绝缘介质。三种电极结构分别为A0-M0-M1-A1结构(①)、M0-A0-M1-A1结构(②)、A1-M2-M3-A2结构(③)。现有双侧向、阵列侧向电极系大部分采用结构①,一般位于电极系中间位置;为了缩短电极系整体长度,提高纵向分辨率,结构②将监督电极M0置于电极系中间位置,并将主电极等分为A0、A0′[7];结构③常见于阵列侧向电极系中,通过增加类似结构③的电极串,实现阵列测量[4, 9]。纵向分辨率主要由电极距决定,电极距越小,纵向分辨能力越强。主电极和监督电极尺寸变化较小。以下主要分析三种结构中各绝缘段和屏蔽电极长度对电极系数、井眼影响和径向探测深度的影响。
|
| ①A0-M0-M1-A1结构;②M0-A0-M1-A1结构;③A1-M2-M3-A2结构。 图 2 侧向测井常见电极结构 Figure 2 Common electrode structures of laterolog |
|
|
利用均质地层方法计算电极系数K[16]。令井径d=8 in①,Rm=0.1 Ω·m,Rt=10 Ω·m,Rxo=1.0 Ω·m,计算井眼影响系数Rt/Ra(Ra为测量得到的视电阻率),并按照伪几何因子J=0.5对应的侵入半径计算径向探测深度。主电极、监督电极长度分别固定为0.03、0.02 m。图 3给出了2.1节中三种侧向测井电极结构对电极系数、井眼影响系数和径向探测深度的影响。
①in (英寸)为非法定计量单位,1 in=2.54 cm,下同。

|
| dA0M0表示电极A0与电极M0之间的距离,其他以此类推;lA1表示电极A1的长度,其他以此类推。 图 3 三种侧向测井电极结构对电极系数、井眼影响、径向探测深度的影响 Figure 3 Effect of three laterolog electrode structures on K factor, borehole effect and radial investigation depth |
|
|
整体上,三种结构对探测特性影响存在差异。对于电极系数:靠近电极系中心的第一段绝缘长度dA0M0(结构①)、dM0A0(结构②)、dA1M2(结构③)的增加使得电极系数迅速增大;另外,只有dM0M1(结构①)保持类似的变化趋势,而其他部分长度的增加皆使得电极系数不同程度地减小。对于井眼影响系数,结构①中四个部分、结构②中dM0A0、结构③中dA1M2的增大皆使井眼影响系数减小,结构②、③其余部分使井眼影响系数不同程度地增加。对于径向探测深度,除了结构②中的dM0A0以外,其余所有部分长度的增加皆使得探测深度不同程度地增加。改变电极系结构,相应地改变了电极系及地层中的电势分布,从而影响了探测特性。例如,增加屏蔽电极A2的长度,提高了屏蔽电流对主电流的聚焦能力,目的层对响应的贡献增加,径向探测深度相应增大。
另外,从图 3还可以得出,屏蔽电极主要影响径向探测深度,而绝缘部分对三种特性都有较大的影响。结构②、③中,各绝缘部分对井眼影响系数的影响具有相反的变化趋势,例如,结构②中dM0A0的增加使得井眼影响系数减小,dA0M1的增加使得井眼影响系数增加。这种相反的变化趋势有利于井眼影响调节,使得井眼影响系数在1.0附近。因此,在电极系设计过程中应重视绝缘段长度对探测特性的影响。
选择普通双侧向电极系,电极系尺寸为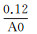

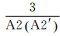
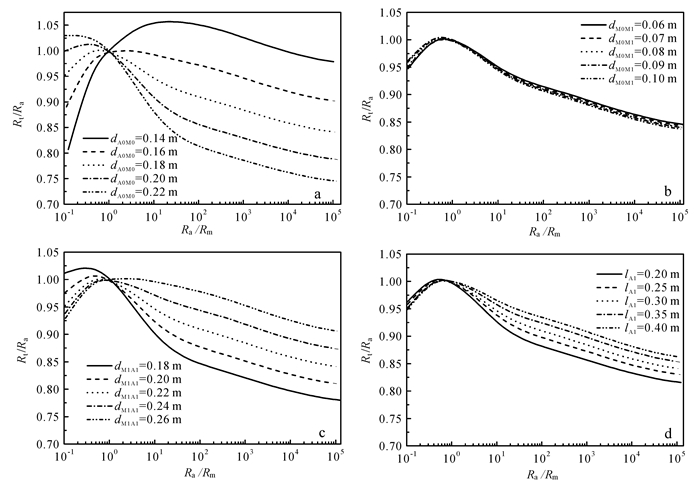
|
| 图 4 结构①对浅侧向井眼影响系数的影响 Figure 4 Effect of structure ① on borehole effect of shallow laterolog |
|
|
①该节部分数据曾在EAGE第七届圣彼得堡国际地质和地球物理会议及博览会(2016.04.11-2016.04.14)上以摘要的形式宣读。
3.1 聚焦原理在盐水泥浆和高阻地层环境中,侧向测井利用电流聚焦作用实现对地层电阻率的测量。按照聚焦实现过程分为硬件聚焦和软件聚焦,按照电位分布大小分为过聚焦和欠聚焦。硬件聚焦电路采用闭环实现主监控,反馈电路不能保证监督电极M0、M1电位差严格为0[3],并受温度、电源波动等外围环境影响[17],监督电极残余电位差难以消除,影响视电阻率测量的准确性。软件聚焦利用电位场叠加原理,将非聚焦形态的电流合成聚焦形态电流,聚焦条件无条件满足。以下以深侧向为例讨论聚焦原理,电极尺寸与2.2节中所述一致,平衡聚焦条件为UM0(M0′)=UM1(M1′),UA1(A1′)=UA2(A2′)。
硬件聚焦中,聚焦条件满足
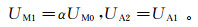 (9)
(9) 式中:UM0、UM1、UA1、UA2分别表示监督电极M0、M1、屏蔽电极A1、A2的电位值;α表示监督电极的残余电位差系数。在数值模拟过程中,α从0.990变化到1.010,间隔为0.002,共11个值,残余电位差比例范围为±0.01。
为实现阵列化测量,引入聚焦系数β,利用软件聚焦使得监督电极M0、M1的电位严格相等,聚焦条件满足
 (10)
(10) 在数值模拟过程中,β取0.00~0.90(欠聚焦,间隔为0.10)、1.00(平衡聚焦)、1.05和1.10(过聚焦),共13个值。
建立如图 5所示的3个分电位场,从左至右,主电极A0、屏蔽电极A1(A1′)、屏蔽电极A2(A2′)分别发射单位电流,其余电极不发射电流,分别测量各电位场中电极M0、M1、A1、A2的电位大小,记为UM0i,UM1i,UA1i,UA2i(i=1, 2, 3, 表示电位场序号)。假设主电极A0发射单位电流并保持不变,根据电位场叠加原理及聚焦条件(9)、(10)得出
 (11)
(11)

|
| 图 5 深侧向测井的三个分电位场 Figure 5 Three potential fields of deep laterolog |
|
|
式中,I1、I2分别表示满足聚焦条件时屏蔽电极A1(A1′)、A2(A2′)发射的电流。
此时,监督电极M0的电位表示为
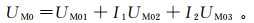 (12)
(12) 视电阻率计算公式为
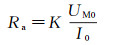 (13)
(13) 式中,I0为主电极A0的发射电流,此处设置为1 A。将式(12)代入式(13)中即可计算出视电阻率。通过改变残余电位差系数α的大小即可分析硬件聚焦中监督电极残余电位差对测井响应的影响;通过调节聚焦系数β得到不同聚焦条件下的测井响应,实现阵列化测量。
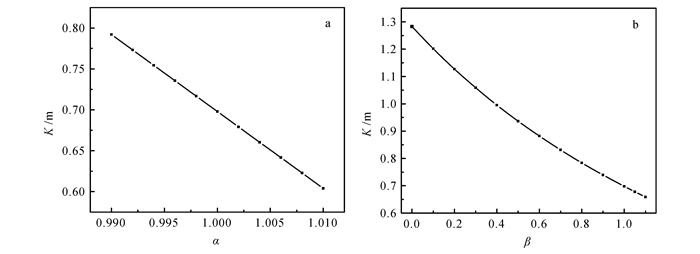
3.2 电极系数图 6给出了电极系数K随α、β的变化曲线。从图 6中可以看出,随着α、β的增加,电流聚焦作用增强,K值减小。其中,K值随α增加呈线性减小,随β增加呈指数趋势减小,拟合公式分别为:
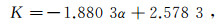 (14)
(14) 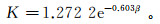 (15)
(15)
|
| 图 6 电极系数随α、β变化曲线 Figure 6 K factor with the change of α, β |
|
|
电极系数对α的变化更为敏感,其原因是监督电极M0、M1与主电极A0的距离更小,残余电位差变化对主电流形态影响更大。
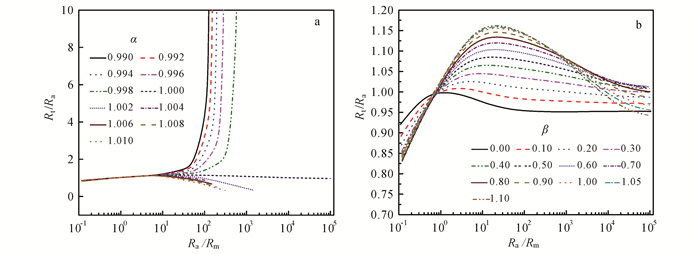
3.3 井眼影响模拟条件:d=8 in,Rm=0.1 Ω·m。图 7给出了井眼影响系数随α、β的变化曲线。从图 7a中可以看出,硬件聚焦中监督电极M0、M1的残余电位差系数严重影响视电阻率的测量。若α=1.000,在整个地层电阻率Rt范围内,井眼影响系数都在1.0左右,井眼影响非常小。若α < 1.000,井眼影响系数曲线发生很大变化,当Rt>10 Ω·m (Ra/Rm>50)时,井眼影响系数明显增大,说明此时测量视电阻率受监督电极残余电位差影响很大,使得测量结果准确性大幅下降。若α > 1.000,曲线发生变化:当Rt>10 Ω·m时,井眼影响系数减小,对应曲线偏离α=1.000时的井眼影响曲线;当Rt继续增大到50 Ω·m (Ra/Rm=100)时,视电阻率出现负值(未画出),测量结果严重失真,而且α越大,失真越强烈。
利用软件聚焦原理使得监督电极M0、M1电位差严格为0,改变屏蔽电极A1、A2电位的相对大小,计算UA2=βUA1时的井眼影响曲线,结果如图 7b所示。图 7b中所有曲线都经过Rt=Rm=0.1 Ω·m的对应点。当Ra>Rm时,β从0.00变化到0.80,对应井眼影响系数增大;β从0.90变化到1.10,在高阻层,对应井眼影响系数略有减小。当Ra<Rm时,β越大,对应井眼影响系数越小。在整个Rt范围内,井眼影响系数都在0.80~1.16范围内,不会出现硬件聚焦中井眼影响系数大幅增加甚至失真的情况。对比分析图 7a、b后认为,在测量过程中,硬件聚焦精度严重影响测量结果的准确性,而通过软件聚焦,使得监督电极M0、M1电位差严格为0,消除了监督电极残余电位差的影响,使得测量结果更加可靠,且改变聚焦系数大小可以得到阵列化的井眼影响曲线。
|
| 图 7 井眼影响系数随α、β变化曲线 Figure 7 Borehole effect with the change of α, β |
|
|
利用伪几何因子J表征侧向测井对泥浆侵入地层的测井响应。模拟条件:d=8 in,Rm=0.1 Ω·m,Rxo=1 Ω·m,Rt=1 Ω·m。图 8给出了J随α、β的变化曲线。在图 8a中:当α从0.990增加到1.000,径向探测深度(按J=0.5对应的侵入半径计算)增加;当α>1.004时,伪几何因子在ri < 1.0 m时出现失真情况。因此,硬件聚焦中监督电极M0、M1的残余电位差严重干扰了侧向测井在泥浆侵入地层中的测量响应。

|
| ri为侵入半径。 图 8 伪几何因子随α、β变化曲线 Figure 8 Pseudo geometrical factor with the change of α, β |
|
|
利用软件聚焦原理使监督电极M0、M1电位差严格为0,改变屏蔽电极A1、A2电位的相对大小,可以获得阵列化的伪几何因子曲线,如图 8b所示。从图 8b可以看出:当β等于0.00、0.50、0.80、0.90、1.00时,对应的探测深度分别为0.38、0.50、0.60、0.78、1.35 m,径向探测深度依次增加;而且,当β=1.10时,J曲线随着侵入半径的增加出现先增大后减小再增加的变化趋势,两个“拐点”对应的侵入半径分别为0.38 m、0.90 m,对应的径向探测深度可以达到2.0 m以上。因此,利用软件聚焦原理在消除监督电极M0、M1电位差影响的同时,引入聚焦系数,改变屏蔽电极A1、A2电位相对大小,可以获得阵列化的具有不同径向探测深度的响应曲线,获得更丰富的地层侵入信息。
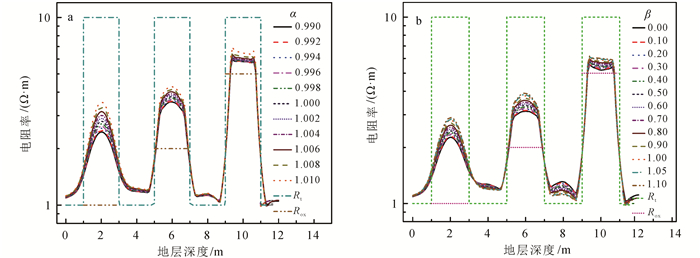
建立侵入地层模型,模拟条件:d=8 in,Rm=0.1 Ω·m,Rt=10 Ω·m,Rs=1 Ω·m,ri=0.5 m,Rxo分别为1、2、5 Ω·m,目的层厚度H为2.0 m,目的层间隔为2.0 m。图 9给出了不同α、β条件下侵入地层中的模拟测量曲线。从图 9中可以看出,在侵入地层中,改变α、β,各模拟测量曲线出现分离,α、β越大,视电阻率值越大,说明原状地层电阻率对测量结果贡献越大。
|
| 图 9 侵入地层模型响应曲线 Figure 9 Response in invasion formation model |
|
|
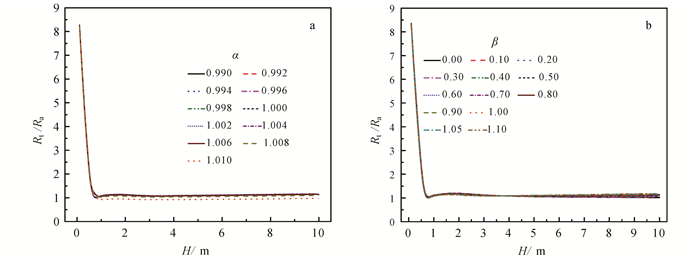
模拟条件: d=8 in,Rm=0.1 Ω·m,Rt=10 Ω·m,Rs=1 Ω·m,改变目的层厚度,图 10给出了不同α、β值条件下的纵向分辨率曲线。从图 10可以看出:随着目的层厚度从0.1 m增加,围岩影响系数快速减小,当目的层厚度为0.6 m时,围岩影响系数接近于1.0;不同α值对应的纵向分辨率曲线稍出现分离,影响不大;不同β值条件下的纵向分辨率曲线几乎重合,说明纵向分辨率基本不受屏蔽电极A1、A2电位相对大小的影响,软件聚焦实现阵列化测量的同时,保持了纵向分层能力的稳定性。
|
| 图 10 纵向分辨率曲线 Figure 10 Longitudinal resolution with the change of α, β |
|
|
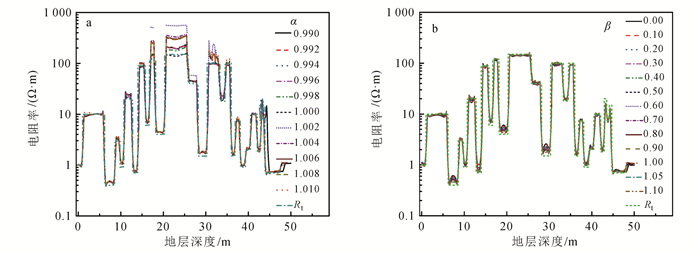
图 11给出了不同α、β取值时Oklamoha标准地层[18]中的测井曲线,地层电阻率变化范围为0.4~150 Ω·m,各分层的厚度变化范围为0.6~5.5 m。从图 11可以看出:在高阻层中,硬件聚焦中监督电极M0、M1之间存在电位差时,测量结果偏离地层电阻率;而且,当α>1.000时,测量曲线不连续,出现失真现象。软件聚焦使得监督电极M0、M1严格等电位,不同β取值下的测量曲线与地层电阻率曲线吻合,没有出现失真现象。
|
| 图 11 Oklamoha标准地层模拟测井曲线 Figure 11 Simulated logging curve in Oklamoha standard formation |
|
|
本文采用有限元数值模拟方法研究侧向测井电极系结构对测井响应的影响,对比硬件聚焦方式,提出一种利用软件聚焦实现的阵列化测量新方法,为电极系设计优化和聚焦方法提供理论指导,得到结论如下:
1)不同电极系结构,电极系不同部分对测井响应的影响不同。整体上,屏蔽电极长度主要影响径向探测深度,绝缘部分对电极系数、井眼影响、径向探测深度都有较大影响;因此,在电极系设计过程中应重视绝缘部分对测井响应的影响。
2)硬件聚焦方式中,监督电极存在残余电位差,严重影响测井响应,尤其是当监督电极M1电位大于M0电位时出现失真现象。采用软件聚焦方式并引入软件聚焦系数,通过改变聚焦系数大小,井眼影响校正曲线稍有变化,井眼影响系数范围为0.80~1.16,在不改变双侧向测井电极系结构基础上可以得到多种径向探测深度,并提高径向探测范围,获得更丰富的地层电阻率径向分布信息。该方法可以直接使用传统双侧向测井电极系结构,结构简单,易于实现。在以后的研究工作中,需要进一步开展不同聚焦系数条件下的数据处理方法研究。
| [1] | Suau J, Grimaldi P, Poupon A, et al. The Dual La-terolog: Rxo Tool[C]//Fall Meeting of the Society of Petroleum Engineers of AIME. San Antonio: Society of Petroleum Engineers Inc, 1972: 1-44. |
| [2] | Davies D H, Faivre O, Gounot M T. Azimuthal Re-sistivity Imaging: A New-Generation Laterolog[J]. SPE Formation Evaluation, 1994, 9 (3) : 165-174. DOI:10.2118/24676-PA |
| [3] | Smits J, Benimeli D, Dubourg I, et al. High Re-solution from a New Laterolog with Azimuthal Imaging[C]//Annual Technical Conference and Exhibition. Dallas: Society of Petroleum Engineers Inc, 1995: 563-576. |
| [4] | Smits J, Dubourg I, Luling M G, et al. Improved Resistivity Interpretation Utilizing a New Array Laterolog Tool and Associated Inversion Processing[C]//Annual Technical Conference and Exhibition. New Orleans: Society of Petroleum Engineers Inc, 1998: 831-843. |
| [5] | Itskovich G, Mezzatesta A, Strack K, et al. High-Definition Lateral Log-Resistivity Device: Basic Physics and Resolution[C]//SPWLA 39th Annual Logging Symposium. Keystone: Society of Petrophysicists & Well Log Analysts, 1998:1-12. |
| [6] | Li S J, Martin L E S, Bittar S M, et al. Multi-Array Laterolog Tools and Methods with Differential Voltage Measurements: US Patent, 2013/0234718 A1[P]. 2013:9-12. |
| [7] | 朱军, 冯琳伟, 李剑浩, 等. 一种新型的高分辨率双侧向测井方法[J]. 测井技术, 2007, 31 (2) : 118-123. Zhu Jun, Feng Linwei, Li Jianhao, et al. A New High Resolution Dual Laterolog Logging Method[J]. Well Logging Technology, 2007, 31 (2) : 118-123. |
| [8] | 童茂松, 宋建华. 0.2 m分辨率双侧向测井仪器数值模拟[J]. 地球物理学进展, 2014, 29 (5) : 2251-2257. Tong Maosong, Song Jianhua. Numeric Simulation of 0.2 m Vertical-Resolution Dual Laterolog Tool[J]. Progress in Geophysics, 2014, 29 (5) : 2251-2257. |
| [9] | 贺飞, 马骁, 冯琳伟, 等. HAL6505阵列侧向测井仪[J]. 石油科技论坛, 2013, 32 (2) : 59-62. He Fei, Ma Xiao, Feng Linwei, et al. HAL6505 Array Laterolog Logging Tool[J]. Oil Forum, 2013, 32 (2) : 59-62. |
| [10] | 朱军, 黄继贞, 汪功礼, 等.贴井壁方位电阻率测井研究[C]//第十二届测井年会论文集.北京:石油工业出版社, 2001: 68-73. Zhu Jun, Huang Jizhen, Wang Gongli, et al. Sidewall Way Azimuthal Resistivity Logging[C]//The 12th Logging Symposium Proceedings. Beijing: Petroleum Industry Press, 2001: 68-73. |
| [11] | Yin C F, Ke S Z, Xu Wei, et al. 3D Laterolog Array Sonde Design and Response Simulation[J]. Applied Geophysics, 2014, 11 (2) : 223-234. DOI:10.1007/s11770-014-0439-z |
| [12] | 丁柱, 陈国华, 王艳梅, 等. 数值合成聚焦原理及算法实现[J]. 国外测井技术, 2001, 16 (2) : 8-9. Ding Zhu, Chen Guohua, Wang Yanmei, et al. Numerical Synthesis Focusing Principle and Algorithm Implementation[J]. Foreign Well Logging Technology, 2001, 16 (2) : 8-9. |
| [13] | 胡海涛, 白庆杰, 肖占山, 等. 基于合成聚焦的高分辨率侧向测井仪数值模拟研究[J]. 地球物理学进展, 2014, 29 (5) : 2178-2182. Hu Haitao, Bai Qingjie, Xiao Zhanshan, et al. Numerical Simulation of High Resolution Laterolog Tool Based on Computed Focusing[J]. Progress in Geophysics, 2014, 29 (5) : 2178-2182. |
| [14] | 祝鹏, 林承焰, 李智强, 等. 水平井和大斜度井中阵列侧向测井响应数值模拟[J]. 吉林大学学报(地球科学版), 2015, 45 (6) : 1862-1869. Zhu Peng, Lin Chengyan, Li Zhiqiang, et al. Numerical Simulation of Array Laterolog Response in Horizontal and Highly Deviated Wells[J]. Journal of Jilin University (Earth Science Edition), 2015, 45 (6) : 1862-1869. |
| [15] | 李大潜, 郑宋穆, 谭永基, 等. 有限元素在电法测井中的应用 [M]. 北京: 石油工业出版社, 1980 . Li Daqian, Zheng Songmu, Tan Yongji, et al. The Application of Finite-Element Method in Electric Well Logging [M]. Beijing: Petroleum Industry Press, 1980 . |
| [16] | 张庚骥. 电法测井 [M]. 北京: 石油工业出版社, 1992 . Zhang Gengji. Electrical Logging [M]. Beijing: Petroleum Industry Press, 1992 . |
| [17] | 梁晓成, 宋建华, 苑娜. 软件聚焦在双侧向测井仪器中的应用[J]. 电子世界, 2013 (17) : 116. Liang Xiaocheng, Song Jianhua, Yuan Na. Application of Software Focusing in Dual Laterolog Instrument[J]. Electronics World, 2013 (17) : 116. |
| [18] | Gao G Z. Simulation of Borehole Electromagnetic Measurements in Dipping and Anisotropic Rock Formations and Inversion of Array Induction Data[D]. Austin: the University of Texas at Austin, 2005. |


