0 引言
地震数据处理要求地震数据的密集性和规则性。一方面,由于受到地质环境、经济条件等诸多条件的限制,往往采集到的地震数据都是不规则的,很难从中获得完整的波场信息;另一方面,当前油气勘探目标构造和环境越来越复杂,使获得的深层地震数据能量很弱,缺失亦很严重。缺失的地震数据直接影响后续去噪、多次波压制和偏移成像的效果,最终影响到地质解释工作。在地震数据处理流程中,对不规则的、稀疏的或者缺失的地震数据进行插值处理,可以避免多次波的预测错误和成像假频等现象,使地震数据处理更加精准。所以,对地震数据进行插值尤为关键。
常见的地震数据插值方法大致分为三类。一是基于波场算子的插值方法。这类方法结合了波动方程与倾角时差校正(DMO)算子[1]、方位角时差校正(AMO)算子[2]进行插值。但由于波动方程计算量很大,而且不能准确获取地下的速度信息,因而限制了该方法的应用。二是基于预测滤波的数据插值方法。Spitz[3]提出了FX域地震插值方法,计算效率和插值效果相比波场算子插值方法有了很大的提高,是实际工作中最常使用的一种方法。Gulunay等[4]提出在FK域进行插值,它和后来提出的TX域插值方法都是基于分频预测的思想。三是近些年发展的基于数学变换的插值方法,即将地震数据从时间域转换到变换域,根据变换域内信号的特征进行插值。如基于傅里叶变换的波场恢复技术,Radon域恢复技术、以及目前在地震数据处理中广泛应用的Curvelet变换[5-8]和Seislet变换[9]。但是这种方法处理效果很大程度上依赖于数学变换的好坏。
传统的地震数据重建遵循Nyquist采样定理,要求采样频率至少是信号最高频率的二倍,并且对数据的规则性要求较高,否则会出现假频现象。压缩感知[10](compressed sensing)理论的提出,使在一定条件下,低于Nyquist采样定理仍然可以恢复出高质量的数据,更多种地震采集方式得以实现,并降低了采集成本。Hennenfent等[11]提出一种jitter采样方式,兼具了规则采样和随机采样的优势,既能控制采样间隔,又能保持采样点的随机性;不仅在野外为地震数据采集提供了更加灵活的采样方式,并且相对于常规的规则采样和随机采样方法有效地减少了假频信息,重构精度也更高。
Herrmann等[12]通过Curvelet稀疏l1范数约束对地震数据进行插值。相比于常规的方法,由于数据是稀疏的或者在变换域是稀疏的,故能够将传统规则采样产生的假频信息转化为低振幅噪声,更好地压制假频信息。尽管Curvelet变换能够很好地对地震数据进行稀疏表示,然而,除了尺度算子和平移算子,Curvelet变换的旋转算子并不能完全数字化;因此,其连续变换和离散变换中不能做统一处理。为了克服Curvelet的缺陷,Kutyniok等[13]通过膨胀仿射系统构成了几乎具最优稀疏表示的Shearlet变换。应用剪切算子可以对Shearlet变换在离散和连续之间做统一处理[14]。
本文介绍Shearlet变换的数学原理以及其相比常规数学方法的优势,结合压缩感知分析基于Shearlet稀疏约束地震插值的基本原理;采用降低假频的jitter采样方式,通过采用基于Landweber加速下降迭代阈值技术[15]提高计算速度;通过理论和实际数据测试验证该方法的重构效果。
1 Shearlet变换简介2005年Guo等[16]和Labate等[17]将复合小波理论和多尺度几何分析有力地联系到一起,通过特殊形式的合成膨胀仿射系统构造了一种接近最优的多维函数稀疏表示方法--Shearlet变换,其具有比曲波和轮廓波更为敏感的方向性和更好的稀疏表示性质。Shearlet变换通过分尺度的手段将图像中的高低频信息用不同的尺度来表示,并且对每个尺度分出不同的方向来表示各向异性特征。因此,Shearlet系统结合了方向算子Os、抛物线尺度算子Aa和平移算子Tm。定义Shearlet变换为
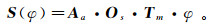 (1)
(1) 式中,φ为母函数。
首先,我们定义算子Os来改变方向性。Curvelet系统的方向特性由基函数的旋转而得到,其旋转方式会损害整数网格,直接导致Curvelet变换在从连续到离散的过程中不能做统一处理。而Shearlet变换采取了不同的方式,其方向性通过剪切矩阵来改变。定义
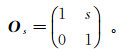 (2)
(2) 式中,s为坡度。利用坡度代替旋转角度的方式使Shearlet变换成为目前多尺度领域唯一能够在离散和连续变换中做统一处理的数学变换。
其次,一个Shearlet系统的母函数由抛物线尺度矩阵Aa或者Ãa构成。当一个轴为aj、另一轴为aj/2时,
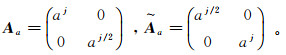 (3)
(3) 如果系统沿着轴向只有一个尺度,那么各向异性特征就不能很好地表示出来。为了得到图像各向异性的最稀疏表示,进行尺度划分是十分必要的。一般来说,尽管有很多比例的尺度化特征可以选择,但是抛物线尺度化特征能更好地表示各向异性特征。
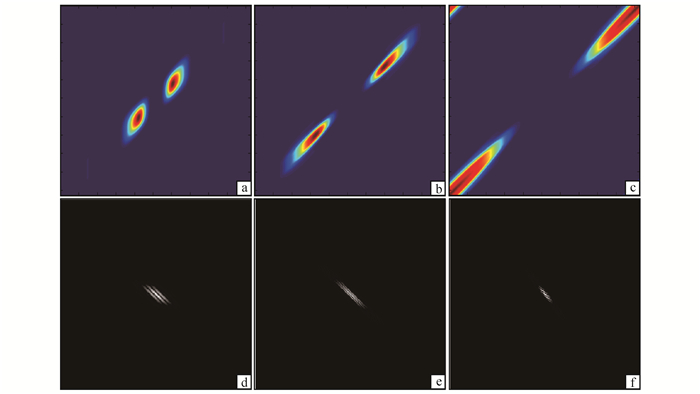
最后,定义一个平移算子来改变母函数:Tm(φ(t))→φ(t-m),基函数φ(t)通过平移参数m进行扩张、剪切、转换得到Shearlet系统。Shearlet系统在可允许的条件下可以表示任何平方可积函数,其方向基函数可以很好地表示出特定方向的高频信息,但是不能很好地表示出低频信息;因此,一般通过一个低通滤波来获取低频信息,即锥适应Shearlet变换。图 1a-c展示了频率域45°方向三个尺度的Shearlet基函数,图 1d-f为对应的空间域Shearlet基函数。
|
| a.频率域第二尺度的一对Shearlet基函数;b.频率域第三尺度的一对Shearlet基函数;c.频率域第四尺度的一对Shearlet基函数;d-f.图a-c对应的空间域Shearlet基函数。 图 1 三个尺度的Shearlet函数 Figure 1 Shearlet elements for three scales |
|
|
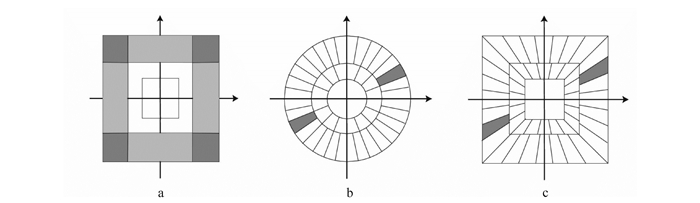
为了更加清晰地展示小波变换、Curvelet变换和Shearlet变换的区别,在图 2中展示了Meyer小波、Curvelet变换以及Shearlet变换的频率域剖分[18-19]。
|
| a.Meyer小波变换;b.Curvelet变换;c. Shearlet变换。 图 2 三种多尺度变换频率域剖分 Figure 2 Frequency tiling of three multiscale transform |
|
|
从图 2中可以分析出:Meyer小波基--正则化的小波基,可以表示各向同性数据;Curvelet基--具有方向性的紧支撑框架,精细尺度可以表示各向异性数据;Shearlet基--具有方向性的紧支撑框架,精细尺度可以很好地表示各向异性数据,且在连续系统和离散系统之间的转变也更加灵活自然,是目前多尺度领域唯一可以将连续系统和数字系统做统一处理的变换方法。
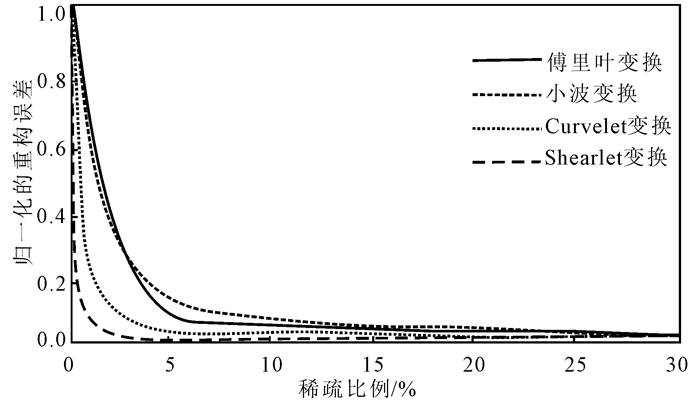
为了说明Shearlet变换的稀疏性更好,将一个合成地震数据分别变换到傅里叶域、小波域、Curvelet域和Shearlet域,分别保留一定比例的最大系数,然后进行逆变换。根据重构地震数据和原始数据的误差来分析这四种变换的稀疏性。图 3为这四种变换的归一化稀疏重构误差,可以看出,在保留相同比例的变换系数时,Shearlet变换的重构误差最小、稀疏性最好。
|
| 图 3 四种变换域归一化重构误差 Figure 3 Reconstruction error in four domains |
|
|
Shearlet变换具有多尺度性、多方向性和局部性,在处理缺失地震信号问题上相对小波变换和脊波变换具有较大的优势,属于各向异性小波。它的基函数能对具有边缘为分段光滑曲线特征的图像进行最稀疏表达,不仅能够表示直线特征和点状特征,而且可以利用多尺度分析的优势对地震反射记录进行最优分解。Shearlet变换的稀疏表示性质即地震数据通过Shearlet变换可以将主要能量集中到小部分Shearlet系数上。通常,有效信号大都集中在Shearlet系数比较大的区域,噪声主要集中在Shearlet系数比较小的区域;通过设置阈值去掉较小的Shearlet系数就可以达到去噪的目的。利用Shearlet变换对地震数据具有稀疏表示的性质,将地震数据去噪问题表示为如下约束最优化问题:
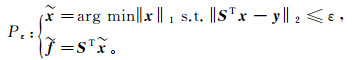 (4)
(4) 式中:y表示原始地震数据(带有噪声的地震数据);x表示Shearlet系数;ST表示Shearlet逆变换;ε表示噪声参量;
Shearlet阈值法在很好抑制随机噪声的同时可以增强地震数据的有效信号,这正是运用Shearlet阈值迭代法进行插值的主要优势。将上述约束最优化问题中加入一个数据缺失算子M,进而得到Shearlet阈值迭代法插值的基本原理。运用该方法将地震缺失数据插值描述为求解如下的l1模最优化问题:
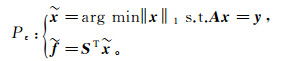 (5)
(5) 式中,A=MST,M为将Shearlet逆变换所得的数据变为原始缺失地震数据的转换算子。
式(5)中的Pε问题可以用一系列简单的优化问题来代替:
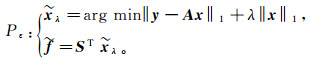 (6)
(6) 式中,λ为拉格朗日算子。如此将问题转换到Shearlet域,反演出一组l1范数最小的Shearlet系数x,重构出地震数据。
为了求解式(6),采用基于Landweber下降法[20]的迭代阈值技术,迭代公式为
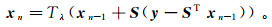 (7)
(7) 式中,阈值函数Tλ(α)=:sgn (α)·max (0, |α|-λ)。为了加快迭代速度,Daubechies等[21]在Landweber阈值下降法研究的基础上,采用了冷却策略(cooling strategy)来降低拉格朗日算子,利用内迭代和外迭代的方式实现求解过程,通过不断修改λ,在内迭代算法中求解公式(7)以获得最优解。首先,在对地震数据进行一次Shearlet变换之后,选取较大的阈值来获取稀疏的Shearlet系数。即初始λ由较大的Shearlet系数决定,这样将少量的解纳入求解范围;然后将上次迭代的解作为下次迭代的输入,并且每次迭代降低λ,使更多的Shearlet系数纳入到解区间来提高求解精度。通过这种方式控制收敛速度,求解步骤可总结如下。
Initial;
i=0;
x0=ATy;
λ0=|ATy|∞;
while‖Ax-y‖2≥ε do
i=i+1;
xi=xi-1;
forl=1 to L do
xi+1=Tλk(xi+ST(y-Sxi));
end for
λk+1←αkλk with 0 < αk < 1;
k←k+1
end while

其中:l为内迭代次数;L为外迭代次数;λk为每次迭代的阈值。
3 模型算例 3.1 理论模型插值试验为了验证Sheratlet变换在地震插值中的效果和保真能力,下面对一个合成地震采用50%jitter欠采样后进行插值。该地震记录共250道、750个采样点,采样间隔4 ms。采用小波变换和Curvelet变换作为稀疏变换对比,结果如图 4所示。为了对比三种方法的插值效果,引进了四个参数进行评价,定义如下。

|
| a.合成数据;b.缺失50%的地震数据;c.小波变换插值;d. Curvelet变换插值;e. Shearlet变换插值;f-h.图c-e对应的差剖面。 图 4 缺失50%地震记录插值对比 Figure 4 Comparison of interpolation after 50% jittered undersampling |
|
|
1)均方差(MSE):
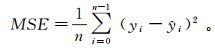
式中:n为采样点数;ŷi为原始无噪声数据;i为去噪后数据。均方差用来表示重构数据和原始数据之间的对应点误差的平方和均值。
2)均方根误差(RMSE):
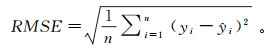
均方根误差用来表示重构值和原始值点对点的误差,能很好地反映出重构的精度。
3)信噪比(SNR):
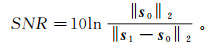
式中:s0表示原始数据;s1表示插值后的数据。
4)峰值信噪比(PSNR):
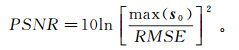
从理论模型测试结果以及表 1所示的评价参数来看:基于小波变换的插值方法(图 4c,SNR=4.316 9 dB)效果并不是很好,在0.5~1.0 s同相轴缺失严重,并且变得不圆滑,差剖面(图 4f)中也有大量能量残留;而基于Curvelet变换的插值效果(图 4d,SNR=13.286 0 dB)要好于小波变换,在信噪比上有很大的提高,残留能量也要少于小波变换,但是同相轴也存在模糊在现象,即插值背景剖面箭头处存在着少量的曲波分量,这种弱信号不利于后续的数据处理工作;而基于Shearlet阈值迭代插值(图 4e,SNR=14.244 7 dB)则取得了令人满意的效果,不仅在信噪比上得到提高,而且插值后的数据同相轴更加清晰细腻。对比三种方法的差剖面(图 4f-h),本文的方法同相轴残余也要少于其他方法,这是由于Shearlet变换能够很好逼近具有各向异性特征的地震数据。
| MSE | RMSE | SNR/dB | PSNR/dB | |
| 小波变换 | 0.002 4 | 0.049 0 | 4.316 9 | 74.324 7 |
| Curvelet变换 | 0.000 3 | 0.017 5 | 13.286 0 | 83.293 9 |
| Shearlet变换 | 0.000 2 | 0.015 6 | 14.244 7 | 84.252 5 |
为了进一步展示本文方法在不同缺失比情况下的插值效果,分别对图 4a数据进行25%、50%以及75%jitter欠采样并进行插值,插值后的数据信噪比分别为24.699 6、14.244 7和6.960 0 dB,结果如图 5所示。从图 5中可以看出:本文方法基本完全重构出缺失比为25%的地震数据;当缺失比为50%时,强能量同相轴稍有损失;即便是缺失比为75%时,本文方法仍然可以很好地重构出地震数据。

|
| a.缺失25%的地震数据;b.缺失50%的地震数据;c.缺失75%的地震数据;d-f.图a-c对应的插值结果;g-i.图a-c插值后对应的差剖面。 图 5 本文方法不同缺失比数据插值 Figure 5 Interpolation on different ratio of sampling data |
|
|
Shearlet变换具有多尺度和多方向性,使得噪声和信号在不同的Shearlet中具有不同的分布特征,即信号的系数会集中在少数幅值较大的Shearlet系数中,而噪声的系数则分布于幅值较小的Shearlet系数中。根据这一特点,应用阈值迭代方法能够减去大部分噪声的系数,从而达到压制噪声、提高信噪比的目的。为此,对缺失比为50%的合成地震记录中分别加入高信噪比(SNR=9.144 6 dB)和低信噪比(SNR=3.021 5 dB)的随机噪声,并用本文方法进行插值,结果如图 6所示。从图 6中可以看出;插值后的地震数据得到很好的恢复,并且噪声得到了很好的压制,从差剖面上基本看不到残留的同相轴;即使在低信噪比的情况下,噪声也得到很好的压制,地震数据得到完整的恢复,差剖面上只有少量弱能量同相轴。

|
| a.含弱噪声的缺失地震数据;b.图a插值后地震数据;c.图a插值后差剖面;d.含强噪声的缺失地震数据;e.图d插值后地震数据;f.图d插值后差剖面。 图 6 本文方法对噪声数据插值 Figure 6 Interpolation on noisy data |
|
|
为了进一步验证Shearlet变换稀疏约束地震数据插值对实际地震数据插值的效果,本文选取某地实际地震数据进行插值,采用的地震数据缺失比为50%。插值结果如图 7所示,评价参数见表 2。
| MSE | RMSE | SNR/dB | PSNR/dB | |
| 小波变换 | 0.002 4 | 0.044 2 | 3.644 6 | 75.221 1 |
| Curvelet变换 | 0.000 3 | 0.018 2 | 11.333 2 | 82.909 7 |
| Shearlet变换 | 0.000 2 | 0.014 8 | 13.156 3 | 84.732 8 |

|
| a.实际数据;b.缺失50%的地震数据;c.小波变换插值;d. Curvelet变换插值;e. Shearlet变换插值;f-h.图c-e对应的差剖面。 图 7 实际数据不同方法插值效果对比 Figure 7 Different methods of interpolation on field data |
|
|
基于小波变换的插值方法(图 7c,SNR=3.644 6 dB)插值效果不是很好,由于小波基只有有限的方向,所以不能够很好地表示弯曲的地震同相轴,浅层强同相轴插值效果欠佳,差剖面大量残留能量可见。基于Curvelet变换的插值方法(图 7d,SNR=11.333 2 dB)取得了较好的效果,插值后的同相轴能量得到很好的恢复。与小波变换不同,Curvelet变换具有各向异性基函数,可以很好地对地震波前进行检测,所以对地震数据进行插值也可以取得很好的效果;但是,它在同相轴曲率大的地方有着明显的“尖角效应”,即大曲率同相轴部分会变得模糊不清。而Shearlet变换具有更好的稀疏性以及更加完备的数学结构,解决了Curvelet变换对大曲率同相轴不能很好表示的问题。对比图 7d、e箭头处可以看出,基于Shearlet变换的地震数据插值(图 7e,SNR=11.333 2 dB)具有更好的插值效果。差剖面中也可明显看出,基于Curvelet变换的插值后仍然残留大量数据(图 7g),这些数据以及其产生的假频都会对后续的偏移成像等产生影响,非常不利于细微构造以及深部地质信息的提取。
从表 2的评价参数可以看出,在地震数据插值问题上,Curvelet变换和Shearlet变换的插值效果相比小波变换都有较大的提高,而Shearlet变换比Curvelet变换更加优秀。
4 结论1) Shearlet变换是一种多尺度稀疏变换,并且具有更好的方向性、稀疏性以及更加完备的数学结构。阈值迭代方法则是在稀疏约束优化反演的背景下得到的方法。
2)将Shearlet变换与阈值迭代方法结合运用到地震数据重构上,能够在保证求解精度的同时降低计算时间。
3) Shearlet变换在jitter采样下能够有效地重构出震数据,并且具有很好的抗噪性。更加多样的采集方式以及联合去噪插值将是未来研究的方向。
| [1] | Canning A, Gardner G H F. Regularizing 3-D Data Sets with DMO[J]. Geophysics, 2012, 61 (4) : 1103-1114. |
| [2] | Chemingui N, Chemingui N. Handling the Irregular Geometry in Wide-Azimuth Surveys[J]. Seg Technical Program Expanded Abstracts, 1999, 15 (1) : 2106. |
| [3] | Spitz S. Seismic Trace Interpolation in the F-X Do-main[J]. Geophysics, 2012, 56 (6) : 785. |
| [4] | Gulunay N. Unaliased f-k Domain Trace Interpo-lation (UFKI)[J]. Seg Technical Program Expanded Abstracts, 1996, 15 (1) : 2106. |
| [5] | Herrmann F J, Gilles H. Non-Parametric Seismic Data Recovery with Curvelet Frames[J]. Geophysical Journal International, 2008, 173 (1) : 233-248. DOI:10.1111/gji.2008.173.issue-1 |
| [6] | Wang D, Bao W, Xu S, et al. Seismic Data Inter-polation with Curvelet Domain Sparse Constrained Inversion[J]. Journal of Seismic Exploration, 2014, 23 (1) : 89-102. |
| [7] | 路交通, 曹思远, 董建华. 基于稀疏变换的地震数据重构方法[J]. 物探与化探, 2013, 37 (1) : 175-179. Lu Jiaotong, Cao Siyuan, Dong Jianhua. A Study of Seismic Data Recovery Based on Sparse Transform[J]. Geophysical & Geochemical Exploration, 2013, 37 (1) : 175-179. |
| [8] | Wang D L, Tong Z F, Tang C, et al. An Iterative Curvelet Thresholding Algorithm for Seismic Random Noise Attenuation[J]. Applied Geophysics, 2010, 7 (4) : 315-324. DOI:10.1007/s11770-010-0259-8 |
| [9] | 刘财, 崔芳姿, 刘洋, 等. 基于低信噪比条件下新型Seislet变换的阈值去噪方法[J]. 吉林大学学报(地球科学版), 2015, 45 (1) : 293-301. Liu Cai, Cui Fangzi, Liu Yang, et al. Threshold Denoising Method Based on New Seislet Transform in the Condition of Low SNR[J]. Journal of Jilin University (Earth Science Edition), 2015, 45 (1) : 293-301. |
| [10] | Candè E J, Wakin M B. An Introduction to Compre-ssive Sampling[J]. IEEE Signal Processing Magazine, 2008, 25 (2) : 21-30. DOI:10.1109/MSP.2007.914731 |
| [11] | Hennenfent G, Herrmann F J. Simply Denoise: Wa-vefield Reconstruction via Jittered Undersampling[J]. Geophysics, 2008, 73 (3) : V19-V28. DOI:10.1190/1.2841038 |
| [12] | Herrmann F J, Wang D, Hennenfent G, et al. Cur-velet-Based Seismic Data Processing: A Multiscale and Nonlinear Approach[J]. Geophysics, 2008, 73 (1) : 2220. |
| [13] | Kutyniok G, Lim W Q. Compactly Supported Shear-lets Are Optimally Sparse[J]. Journal of Approximation Theory, 2011, 163 (11) : 1564-1589. DOI:10.1016/j.jat.2011.06.005 |
| [14] | Kittipoom P, Kutyniok G, Lim W Q. Construction of Compactly Supported Shearlet Frames[J]. Constructive Approximation, 2012, 35 (1) : 21-72. DOI:10.1007/s00365-011-9142-y |
| [15] | Daubechies I, Fornasier M, Loris I. Accelerated Pro-jected Gradient Method for Linear Inverse Problems with Sparsity Constraints[J]. Journal of Fourier Analysis and Applications, 2008, 14 (5/6) : 746-792. |
| [16] | Guo K, Kutyniok G, Labate D. Sparse Multidimen-sional Representations Using Anisotropic Dilation and Shear Operators[C]//International Conference on the Interaction. Athens: Wavelets and Splines, 2005:189-201. |
| [17] | Labate D, Kutyniok G. Sparse Multidimensional Re-presentation Using Shearlets[C]//Proceedings of SPIE.[S. l.]: The International Society for Optical Engineering, 2005, 5914(1):254-262. |
| [18] | Kutyniok G, Shahram M, Zhuang X. ShearLab: A Rational Design of a Digital Parabolic Scaling Algorithm[J]. Siam Journal on Imaging Sciences, 2011, 5 (4) : 1291-1332. |
| [19] | Kittipoom P, Kutyniok G, Lim W Q. Construction of Compactly Supported Shearlet Frames[J]. Constructive Approximation, 2012, 35 (1) : 21-72. DOI:10.1007/s00365-011-9142-y |
| [20] | Vogel C R. Computational Methods for Inverse Pro-blems [M]. Philadelphia: Society for Industrial and Applied Mathematics, 2002 . |
| [21] | Daubechies I, Defrise M, Mol C D. An Iterative Th-resholding Algorithm for Linear Inverse Problems with a Sparsity Constrains[J]. Communications on Pure and Applied Mathematics, 2004, 57 (11) : 1413-1457. DOI:10.1002/(ISSN)1097-0312 |



