0 引言
作为一种沿中心射线传播的局部瞬态场,delta波包源自高斯波束,是高斯波束在时空域的对偶表示。2016年,笔者[1-2]将其引入到偏移领域:利用delta波包叠加表达时间域格林函数,通过互相关成像条件,给出了深度偏移算法。基于delta波包叠加的深度偏移算法既继承了高斯波束偏移的诸多优点,如包含多波至走时、计算焦散区振幅、处理陡倾角等,又保留了射线类偏移方法的缺陷,如高速岩问题。
高速岩是地震勘探中经常遇见的棘手情况。随着陆地和浅海探明油气储量的减少,深海油气勘探正成为世界油气勘探的新热点。全球深水油气资源丰富,据2008年资料统计,40%的油气储量发现于浅水( < 500 m),29%的储量发现于深水(>500 m)[3-4]。深海中探明油气储量有相当比重分布在高速岩(如墨西哥湾盐岩、南海火成岩等)下[4-5]。由于这类岩石的发育和构造样式复杂多变,与围岩间速度差异明显,当射线穿过高速岩体时,受折射效应影响,射线密度降低,进而导致delta波包的分布密度降低,使成像质量变差,甚至无法成像。为弥补这一缺陷,我们需要选择一种可以有效提高射线密度的射线追踪算法。
波前构建算法是一种计算地震波走时、射线路径以及射线振幅的快速算法。与传统射线追踪方法不同,波前构建算法不再局限于单条射线追踪计算,而是随波前推进同时计算多条射线。它最早由Vinje等[6]提出,采用样条函数进行插值,适用于二维各向同性介质。随后Coman等[7-8]引入了双三次样条函数差插值方法,韩复兴[9]引入了二维三次卷积插值方法,这两种方法既满足了计算精度又提高了计算效率。Sun等[10]和Vinje等[11]成功实现了三维复杂介质的射线追踪数值计算,孙小东等[12]利用四面体网格剖分,提高了三维介质射线追踪效率。Gibson等[13]、白海军等[14]将波前构建方法拓展到各向异性介质的数值模拟中。
作为一种可同时考虑到整个射线场的计算技巧,波前构建算法在波前推进过程中可随时检验射线场密度,当射线场密度不足时,可通过插入新的射线提高射线覆盖率。本文采用波前构建法的深度偏移算法,在处理具有复杂形状的盐丘模型(如Sigsbee 2A)时,由于射线密度的提升,可有效改善高速体下方区域的成像质量。对于射线插入的标准,在总结前人工作的基础上,采用Coman等[8]和韩复兴[9]的描述。在具体实现上,采用链表结构替代数组结构存储波前信息,以节省CPU耗时。
1 偏移方法原理 1.1 波场表达考虑2维单炮地震记录,震源位置为xs=(xs, 0),地表接收点位置为xr=(xr, 0),地下成像点位置为x=(x, z),根据Claerbout[15]提出的互相关成像条件,有
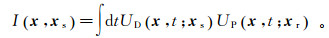 (1)
(1) 式中:I(x, xs)为共炮道集下成像点x处的成像结果;t为时间;UD(x, t; xs)表示由源点xs传播到成像点x的直达波场;UP(x, t; xr)表示由接收点xr反向延拓至成像点x的延拓波场。
根据第一种Rayleigh积分和高频渐近理论,延拓波场UP(x, t; xr)满足表达式[16]
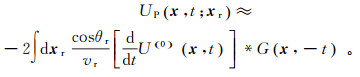 (2)
(2) 式中:vr为接收点xr处的地表速度;θr为接收点xr处射线出射方向与z坐标轴正方向的夹角;U(0)(x, t)为xr处接收到由震源xs引起的地震反射波场;G(x, -t)表示由接收点xr传播到成像点x的时间域格林函数,其中,-t表示反因果传播;*表示褶积。
假设直达波场UD(x, t; xs)由xs处点源产生,其震源函数为f(t),则UD(x, t; xs)满足表达式
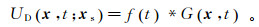 (3)
(3) 式中,G(x, t)表示由源点xs传播到成像点x的时间域格林函数。
1.2 delta波包格林函数表达式不同,使用的偏移方法也不同。若频率域格林函数取AARTexp (iωτART)的形式,可使用常规Kirchhoff偏移,角标ART表示渐近射线理论(asymptotic ray theory),AART为振幅,τART为实走时,ω为频率;若取高斯波束叠加形式,可利用高斯波束叠加法进行深度偏移[16];本文利用delta波包叠加表示时间域格林函数,
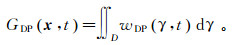 (4)
(4) 式中:wDP(γ, t)被Červený[17]称为delta波包函数,是单条高斯波束在时空域的对偶形式;角标DP表示delta波包(delta packet);γ为射线坐标,用以标识中心射线,二维情况下可取极坐标或笛卡尔坐标;区域D为射线坐标γ的积分范围。式(4)表明,将区域D内delta波包叠加可得时间域格林函数GDP(x, t)。
delta波包是高斯波束在时空域的对偶形式,满足高斯波束的傅里叶逆变换:
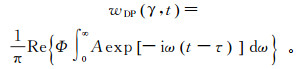 (5)
(5) 式中:权函数Φ、振幅A和走时τ皆为复数,满足高斯波束理论,可利用运动学和动力学射线追踪方程求取[18]。设复走时τ=τR+iτI,其中τR和τI分别为复走时的实部和虚部,并且τI≥0。当振幅与频率无关时,波包函数wDP(γ, t)在时间域存在解析式[17]:
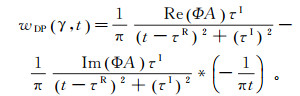 (6)
(6) 利用式(6)可直接在时间域计算波包函数wDP(γ, t)。将公式(6)代入公式(4),可得delta波包叠加形式的时间域格林函数表达式。
1.3 算法流程结合之前的推导,利用delta波包叠加进行时间域深度偏移的计算流程为:1)输入光滑速度场和地震反射数据。因为动力学追踪方程含有速度场的二阶导数,所以需要对速度场的二阶导数进行光滑。2)数值求解运动学和动力学射线追踪方程。3)利用公式(3)、(4)和(6)计算直达波场UD(x, t; xs),再利用公(2)、(4)和(6)计算延拓波场UP(x, t; xr)。4)将直达波场与延拓波场进行互相关成像,可得到单炮偏移记录。5)重复步骤3)和4),将所有单炮偏移记录进行叠加。
2 射线追踪的波前构建法为了将波前构建法与深度偏移算法相结合,需要讨论三个问题:射线插入标准,射线插入方法和波前数据存储。
2.1 插入射线为了能在波前推进时插入新的射线,需要解决什么时候插入射线和如何插入射线两个问题。对于前一个问题,采用Coman[8]和韩复兴[9]的描述,将新射线插入的标准分为三部分:1)同一波前面上相邻射线点间距离大于距离预设值时,插入新射线;2)当不满足条件1)、但相邻射线曲率差大于曲率差预设值时,插入新射线;3)满足条件1)、但两条射线相交时,在交点插入新射线。以上三个条件同时使用时,既避免了小范围内速度异常引起的采样不足,又可控制计算网格节点处的走时误差。
当相邻两条射线满足插入标准时,使用虚拟震源方法进行新射线插入计算[19]。如图 1所示,射线A1和射线A2为两条相邻射线,MA1和MA2分别为它们与波前面的交点,交点处的慢度方向为pA1和pA2。当它们满足插入新射线标准时,过点MA1和MA2分别沿慢度方向pA1和pA2做直线,其直线交点为虚拟震源,直线夹角为α。假设新插入射线由虚拟震源发射,为夹角α的角平分线,根据MA1和MA2到虚拟震源的距离和慢度方向,可确定新插入波前点Mnew的位置。可以看出,利用虚拟震源方法可以快速方便地插入新射线。但需要注意的是,条件1)中判断射线是否插入的距离预设值不宜过大,特别是当介质复杂、速度变化较大时,以减少该方法的数值误差。

|
| 图 1 虚拟震源法示意图 Figure 1 Inserting a new ray by virtual source method |
|
|
进行常规Kirchhoff偏移时,我们只需计算网格节点上的走时和振幅;此时波前构建程序可只保留当前计算的两层波前,而将已被计算过的波前释放掉。但利用delta波包叠加进行深度偏移时,需要使用完整射线路径,这要求波前构建程序必须保留所有波前信息,并从中恢复出射线路径。
为了适应波前构建法频繁进行新射线的插入操作,将使用链表结构对波前数据进行存储。链表是一种重要的计算机存储结构,用它表示线性表时,利用指针表示节点间的逻辑关系。因此,一个存储节点通常包含两个部分:数据(data)和指针(next)。数据域用于存储数据,指针域用于存放下一个节点的地址。用链表存储数据的优点在于可采用动态内存分配,不会造成内存浪费和溢出。链表执行插入和删除操作时,只需修改指针即可,无需移动大量元素[20]。
本文用一条链表存储一条射线,插入新射线等于插入新的链表,同时建立一条射线索引链表用于储存每条射线链表的首节点地址。具体实现方法(图 2)如下:首先,构建一个射线索引链表(图 2中深色阴影部分)。假设有三条射线A1,A2和A3,对应射线索引链表上的3个节点,每个节点主要包含三个地址(以射线A1为例,图 2a):下条射线(A2)的索引链表节点地址(nextA2)、该条射线(A1)的首个波前点地址(nextA11),该条射线(A1)的当前计算波前点地址(nextA13)。其次,每条射线对应一条链表(图 2中浅色阴影部分,以射线A1为例),射线链表的每个节点表示一个波前点,包含两部分(以节点A11为例):下个节点(A12)的地址(nextA12)和当前节点(A11)的数据(dataA11)。数据data主要包含了当前波前点的走时、慢度、振幅等信息。最后,插入新的射线等于插入新的链表(以射线A2和A3间插入新射线Anew为例,图 2b),当插入新链表时,只需将射线索引列表中A2节点中下个节点的地址改为nextAnew、Anew节点中下个节点的地址设为nextA3即可。

|
| a.插入新射线前;b.插入新射线后。 图 2 链表存储示意图 Figure 2 Wavefront data storage in the form of chained lists |
|
|
与常规的数组法相比,链表式存储的优势在于插入射线的效率。假设利用二维数组w[m][n]存储二维波前数据点,m表示波前,n表示射线。当需要在n=i和n=i+1间插入射线时,需要将数组w的一部分w[m][i+1]~w[m][n]整体向右移动到w[m][i+2]~w[m][n+1],以空出原有的w[m][i+1]用来存储新插入的射线。若利用链表储存,则无需这种移动,只需改变节点地址即可。
此外,利用数组存储时,数组的大小在创建时就已固定。数组太大会造成存储空间的浪费;而数组太小,当内存外溢时,需要将原有数组移动到更大的数组,降低了计算效率。链表式存储的另一个优势就是需要多少内存就可以使用多少内存,充分利用现有内存空间。
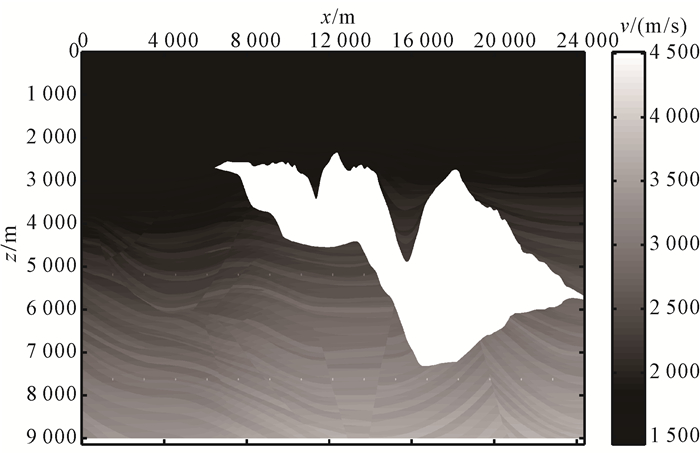
3 数值算例本文选用SMAART公司提供的Sigsbee 2A模型和模拟数据对结合了波前构建法的时间域深度偏移进行试算。图 3为Sigsbee 2A的速度模型。横向网格节点数为2 133,网格间隔为11.43 m;纵向网格节点数为1 201,网格间隔为7.62 m。模拟地震记录共500炮,最大道数为348道,炮间距和道间距均为22.86 m。
|
| 图 3 Sigsbee 2A速度模型 Figure 3 Sigsbee 2A velocity model |
|
|
可以看出,Sigsbee 2A模型包含一个形状复杂的高速体(盐丘),其对波场能量的影响非常复杂。受折射效应影响,盐下区域经常出现射线覆盖率不足的情况。这里选取了位于盐丘上的两个出射点(11 659,0)、(16 231,0)进行射线追踪计算(图 4),射线出射角度范围为[-50°, 50°]。出射点(11 659,0)为第250炮的位置,出射点(16 231,0)为第350炮的位置。为了提高盐下射线覆盖率,射线间隔不采用角度,而采用慢度分量px,即任意相邻两条射线间的出射角角度差是不固定的,但慢度分量px差是固定的。同时选取两种方法进行射线追踪计算:一种是缩小射线间隔,直接在震源对射线条数进行加密(初始射线200条,如图 4a、d);另一种是之前讨论的波前构建法(初始射线100条,插入100条,共200条射线,如图 4b、e;初始射线50条,插入150条,共200条射线,如图 4c、f)。通过对比可以看出,同样是200条射线,与加密射线方法相比,利用波前构建方法进行射线追踪可有效提高盐下区域的射线密度,提升射线覆盖率。但同样是波前构建方法,初始射线不同,射线加密区域却略有区别。这是因为,在我们的波前构建算法中,射线还无法实现精准插入,只能根据波前推进情况进行自动插入,所以初始射线的位置和条数将影响射线追踪的最终结果。虽然射线路径略有不同,但出射点下方对应盐下区域的射线覆盖率都得到了显著提升。

|
| a.点(11 659,0)出射,直接缩小射线间隔,初始射线200条; b.点(11 659,0)出射,初始射线100条,通过波前构建插入新射线100条;c.点(11 659,0)出射,初始射线50条,插入射线150条;d.点(16 231, 0)出射,直接缩小射线间隔,初始射线200条;e.点(16 231, 0)出射,初始射线100条,插入射线100条;f.点(16 231, 0)出射,初始射线50条,插入射线150条。 图 4 插入不同数量射线的单点射线追踪(Sigsbee 2A模型) Figure 4 Ray-tracing results of Sigsbee 2A model with different number of inserted rays |
|
|
表 1给出了数组法和链表法的CPU耗时对比。可以看出:当不插入射线时(初始200条),数组法要略优于链表法,这主要因为数组法寻址要快于链表法;而当需要插入射线时,链表法要明显优于数组法,CPU耗时至少缩短9%,插入新射线越多,CPU耗时越短。
| 出射点(11 659,0) | 出射点(16 231,0) | |||||
| 初始200条 | 初始100条 | 初始50条 | 初始200条 | 初始100条 | 初始50条 | |
| 数组法 | 20.43 | 19.37 | 18.31 | 23.39 | 19.55 | 15.82 |
| 链表法 | 21.12 | 17.17 | 14.74 | 23.67 | 17.69 | 13.38 |
| 注:共200条射线,重复计算50次。 | ||||||
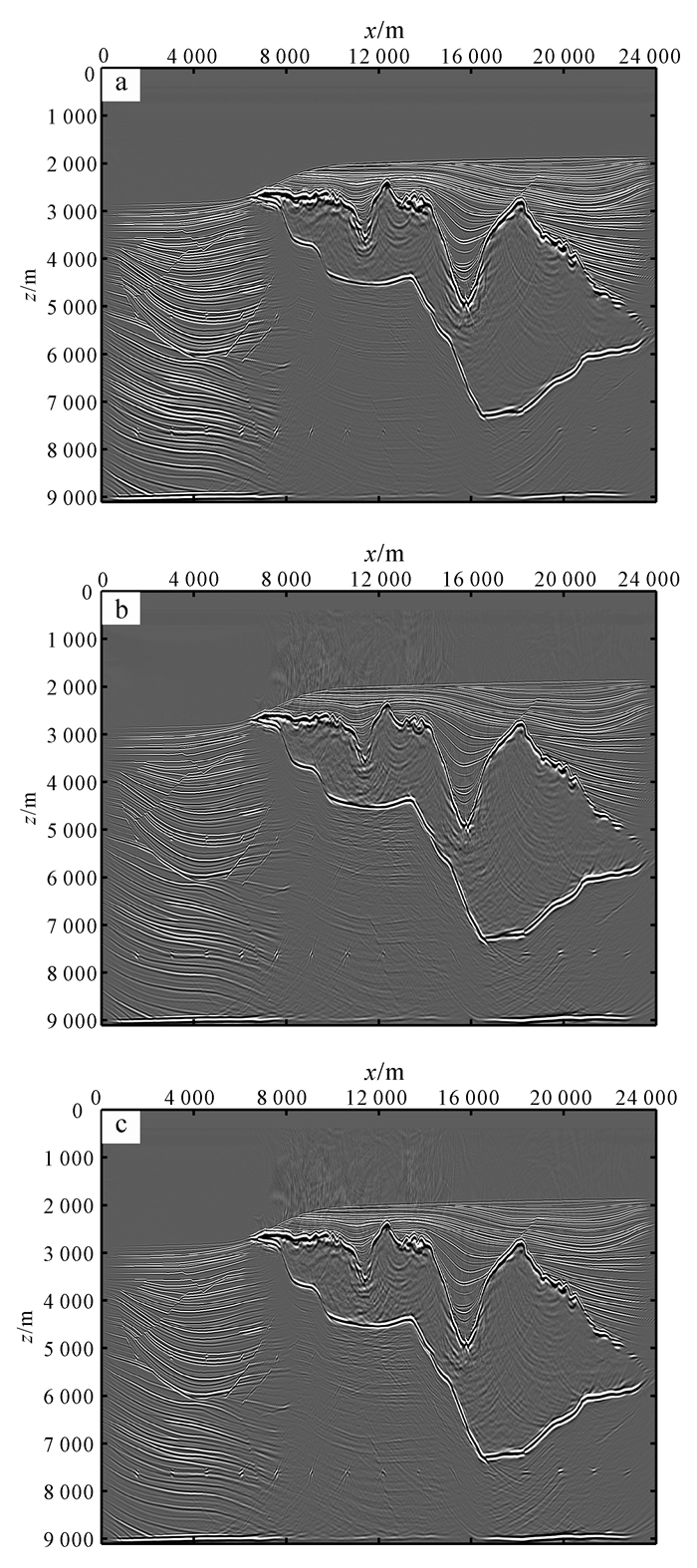
图 5给出了两种不同方法试算出的偏移成像结果。对比图 5a、b、c可知:由于盐下射线覆盖率的提升,结合了波前构建法的偏移结果,其盐下区域的成像能量得到了显著提高;而其他射线覆盖率本就充足的地方,成像结果变化不大。这意味着当射线密度低时,提升射线密度可有效改善成像质量。但需要注意的是,这种成像能量的提升是无法区分有效信号和噪声的,即有效信号和噪声同时得到了加强。
|
| a.直接缩小射线间隔,初始射线200条;b.初始射线100条,通过波前构建插入新射线100条;c.初始射线50条,插入射线150条。 图 5 插入不同数量射线的叠加剖面(Sigsbee 2A模型) Figure 5 Stacked images of Sigsbee 2A model with different number of inserted rays |
|
|
对比图 5b和图 5c可知,虽然插入射线的条数增多,但成像能量并没有明显提高。这意味着当总射线条数固定时,一味提高插入射线数量,并不会无休止地改善成像质量;相反,由于使用虚拟震源法插入新射线,射线插入越多,其引起的数值误差也越大。
4 结论1)本文将波前构建法与基于delta波包叠加的时间域深度偏移相结合,既保留了偏移算法的原有优点,如包含多波至走时、计算焦散区振幅、处理陡倾角等,同时又有效提升了射线覆盖率不足区域的射线密度,改善了成像质量。
2)由于深度偏移算法需要完整射线路径,采用链表结构进行波前数据存储,可简洁地进行射线插入操作,并从中轻易恢复出射线路径。
3) Sigsbee 2A模型的数值试算表明,改进后的偏移算法对于复杂盐丘模型具有良好的成像能力,并且利用链表存储波前信息要比利用数组至少节省9%的CPU耗时。但我们同时注意到,由于使用虚拟震源法插入射线,当插入射线过多时,其引起的数值误差可能降低图像的信噪比。如何更精确、有选择地插入射线,以提高波前构建法的计算精度和计算效率,还需我们做更进一步的研究。
致谢: 吉林大学移动平台探测研发中心对本文提供了计算设备支持,在此表示感谢。| [1] | 石秀林, 孙建国, 孙辉, 等. 基于delta波包叠加的时间域深度偏移[J]. 地球物理学报, 2016, 59 (7) : 2641-2649. Shi Xiulin, Sun Jianguo, Sun Hui, et al. The Time-Domain Depth Migration by the Summation of Delta Packets[J]. Chinese Journal of Geophysics, 2016, 59 (7) : 2641-2649. |
| [2] | 孙建国. 高频渐近散射理论及其在地球物理场数值模拟与反演成像中的应用:研究历史与研究现状概述以及若干新进展[J]. 吉林大学学报(地球科学版), 2016, 46 (4) : 1231-1259. Sun Jianguo. High-Frequency Asymptotic Scattering Theories and Their Applications in Numerical Modeling and Imaging of Geophysical Fields: An Overview of the Research History and the State-of-the-Art, and Some New Developments[J]. Journal of Jilin University (Earth Science Edition), 2016, 46 (4) : 1231-1259. |
| [3] | 洪菲, 胡天跃. 深海油气地震勘探进展和展望[J]. 地球物理学进展, 2002, 17 (2) : 230-236. Hong Fei, Hu Tianyue. Advance and Prospect of Deepwater Hydrocarbon Exploration[J]. Progress in Geophyscis, 2002, 17 (2) : 230-236. |
| [4] | 赵阳, 卢景美, 刘学考, 等. 墨西哥湾深水油气勘探研究特点与发展趋势[J]. 海洋地质前沿, 2014, 30 (6) : 27-32. Zhao Yang, Lu Jingmei, Liu Xuekao, et al. Oil and Gas Exploration in Deep Water Area of Gulf of Mexico[J]. Marine Geology Frontiers, 2014, 30 (6) : 27-32. |
| [5] | 朱伟林, 张功成, 钟锴, 等. 中国南海油气资源前景[J]. 中国工程科学, 2010, 12 (5) : 46-50. Zhu Weilin, Zhang Gongcheng, Zhong Kai, et al. South China Sea Oil and Gas Outlook[J]. Engineering Sciences, 2010, 12 (5) : 46-50. |
| [6] | Vinje V, Iversen E, Gjøystdal H. Traveltime and Am-plitude Estimation Using Wavefront Construction[J]. Geophysics, 1993, 58 (8) : 1157-1166. DOI:10.1190/1.1443499 |
| [7] | Coman R, Gajewski D. 3D Wavefront Constuction Me-thod with Spherical Interpolation[C]//62th EAGE Conference & Exhibition. Glasgow: EAGE, 2000: C43. |
| [8] | Coman R, Gajewski D. 3D Traveltime and Migration Weight Computation Using Wavefront Oriented Ray Tracing[C]//63rd EAGE Conference & Exhibition. Amsterdam: EAGE, 2001: P008. |
| [9] | 韩复兴.论波前构建法中的几个计算问题[D].长春:吉林大学, 2009. Hang Fuxing. On Some Conputational Problems in Wavefront Construction Method[D]. Changchun: Jilin University, 2009. |
| [10] | Sun Y, Clapp R G, Biondi B. Three Dimensional Dy-namic Ray Tracing in Complex Geological Structures[R]. Stanford: Stanford Exploration Projec, 1997: 63-75. |
| [11] | Vinje V, Åstebøl K, Iversen E, et al. 3-D Ray Mo-deling by Wavefront Construction in Open Models[J]. Geophysics, 1999, 64 (6) : 1912-1919. DOI:10.1190/1.1444697 |
| [12] | 孙小东, 李振春, 栗宝鹃, 等. 波前构建法三维射线追踪[J]. 天然气工业, 2008, 27 (Sup. 1) : 275-277. Sun Xiaodong, Li Zhenchun, Li Baojuan, et al. 3-D Ray Tracing by Wavefront Construction[J]. Natural Gas Industry, 2008, 27 (Sup. 1) : 275-277. |
| [13] | Gibson Jr R L, Durussel V, Lee K J. Modeling and Velocity Analysis with a Wavefront-Constrcution Algorithm for Anisotropic Media[J]. Geophysics, 2005, 70 (4) : T63-T74. DOI:10.1190/1.1988188 |
| [14] | 白海军, 孙赞东, 王学军. 基于波前构建法的TTI介质射线追踪[J]. 石油地球物理勘探, 2011, 46 (Sup. 1) : 1-6. Bai Haijun, Sun Zandong, Wang Xuejun. Raytracing in TTI Media Using Wavefront Construction[J]. Oil Geophysical Prospecting, 2011, 46 (Sup. 1) : 1-6. |
| [15] | Claerbout J. Imaging the Earth's Interior[J]. Geo-physical Journal of the Royal Astronomical Society, 1986, 86 (1) : 217. |
| [16] | Popov M M, Semtchenok N M, Popov P M, et al. Depth Migration by the Gaussian Beam Summation Method[J]. Geophysics, 2010, 75 (2) : S81-S93. DOI:10.1190/1.3361651 |
| [17] | Červený V. Synthetic Body Wave Seismograms for Laterally Varying Layered Structures by the Gaussian Beam Method[J]. Geophysical Journal International, 1983, 73 (2) : 389-426. DOI:10.1111/gji.1983.73.issue-2 |
| [18] | Červený V. Seismic Ray Theory [M]. Cambridge: Cambridge University Press, 2005 . |
| [19] | 何洋, 基于波前构建的射线走时和振幅计算[D].长春:吉林大学, 2005. He Yang. Computation of Traveltimes and Amplitudes Based on Wavefront Construction Ray Tracing[D]. Changchun: Jilin University, 2005. http://www.oalib.com/references/19476149 |
| [20] | 李云清. 数据结构 [M]. 北京: 人民邮电出版社, 2004 . Li Yunqing. Data Structure [M]. Beijing: Posts & Telecom Press, 2004 . |



