0 引言
时间域航空电磁法(airborne time-domain electromagnetics, ATEM)具有速度快、成本低、适用性强等特点,非常适合于地形地质条件复杂或环境恶劣(比如沙漠、高山、丛林、湖泊)等地区的资源、能源、环境工程和地下水勘查,是国土资源调查中非常有效的地球物理勘查技术手段。
由于航空电磁数据量巨大,目前主流的解释方法主要有两种:一种是电导率-深度转换(CDI/CDT)的快速成像方法[1-3],另一种是层状大地反演(LEI)方法[4-5]。CDI/CDT方法是一种快速成像方法,不需要设置初始模型,无需进行迭代,计算速度快,能够反映地下电性分布的主要特征,适用于现场的快速处理。LEI方法直接用迭代模型的响应来拟合观测数据,能得到较理想的反演结果,但该方法受初始模型的影响较大,且由于需要进行不断迭代,耗时较长,一般用于后期数据的精细处理和解释。LEI主要包括阻尼最小二乘法[6-7]、模型交替调整反演算法[8]、神经网络方法[9]、自适应正则化反演方法[10]等。
在传统的航空电磁数据反演中,通常假设大地的磁导率等于自由空间磁导率(μr=1),在数据处理过程中忽略磁化效应的影响。这种方法在无磁性地区能获得较好的结果。然而,在一些强磁地区,由于磁化效应影响电磁响应,因此忽略磁导率影响将导致数据处理结果出现较大偏差。Thomas[11]指出,在飞行高度为50 m时,相对磁导率大于等于1.005就会对航空电磁系统产生明显影响。Beard等[12]指出,当地层磁导率不等于自由空间磁导率时,会在航空电磁响应的实分量中出现一个与频率无关的偏移,偏移量随着磁导率的增大、磁性物质的增多和飞行高度的降低而增大。实际上,很多火成岩和变质岩以及由其风化产生的土壤的相对磁导率往往会大于1.005。磁铁矿的平均相对磁导率为7[13],这就意味着,只要地层中的磁铁矿含量为千分之一,整个地层的相对磁导率就会大于1.005。而且,随着飞行高度的降低,磁导率对电磁响应的影响会更加明显。
几十年来,国内外在磁性地层的正反演研究中已经取得了一些成果。Zhang等[14]提出了在一维频率域中假设模型电阻率为已知的条件下求取磁导率的方法,其反演结果的准确性依赖于能否准确获得背景场电阻率信息。Huang等[15]提出了首先用最低频率的同相分量和正交分量计算磁导率,然后利用电磁响应同相分量受磁导率影响大于正交分量的特点,由相邻频率的正交分量计算视电阻率的方法。Zhang等[16]提出了在频率域中将大地假设为多个厚度为已知常数的地层,对大地电阻率和磁导率进行反演的方法。Huang等[17]实现了频率域中层状地层电阻率、磁导率和层厚的反演,并在实测数据的处理中取得了良好效果。覃庆炎等[18]研究了磁导率在时间域电磁响应中的影响特征。殷长春等[19]对时间域航空电磁数据进行加权横向约束反演,由理论和实测数据的反演结果表明了该方法的有效性。然而,基于磁导率模型的时间域航空电磁数据的反演目前尚未见到发表的成果。本文提出了一种时间域航空电磁数据的多参数反演算法。首先研究磁导率对时间域航空电磁响应的影响特征,进而基于阻尼最小二乘法提出对时间域航空电磁数据进行电阻率、磁导率和层厚全时同步反演的方法,并通过对理论仿真数据的反演验证本文算法的有效性。
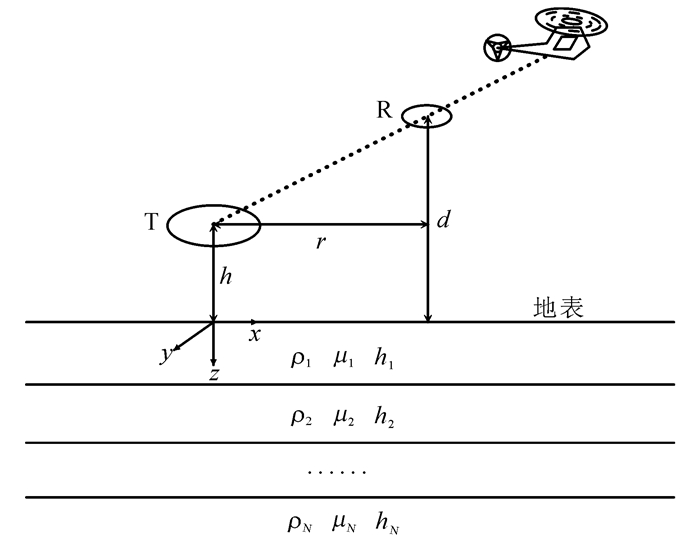
1 正演理论 1.1 时间域航空电磁响应正演计算时间域航空电磁正演模型如图 1所示。对于N层水平层状大地,假设直角坐标系的原点位于磁偶极子源正下方的地表上,z轴向下为正。发射线圈T高度为h,接收线圈R高度为d,发射线圈和接收线圈的水平距离为r,第n层的电阻率为ρn,磁导率为μn,层厚度为hn,则垂直磁偶极子源在接收线圈产生的电磁感应垂直分量Bz表达式[20]为
|
| 图 1 层状大地时间域航空电磁系统模型 Figure 1 ATEM system over a layered earth |
|
|
 (1)
(1) 式中:μ0为真空磁导率;m为发射线圈磁矩;J0为零阶贝塞尔函数;λ为积分变量;rTE为反射系数。
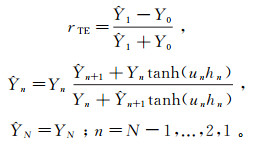 (2)
(2) 其中: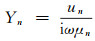
由式(1)计算得到频率域响应后,根据文献[21],可通过反傅里叶变换得到时间域的阶跃响应
Bzs(t):
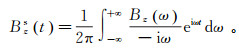 (3)
(3) 式中:Bz(ω)为航空电磁系统的频率域响应;t为时间。式(3)经过简单变换成为
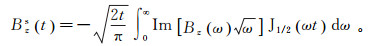 (4)
(4) 式中,J1/2为半整数阶贝塞尔函数。本文使用Yin等[22]给出的160点汉克尔滤波系数对式(4)进行数值计算。
对于任意发射波形,我们可利用如下褶积公式计算时间域航空电磁响应[22]:
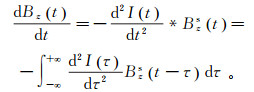 (5)
(5) 式中:I(t)为发射电流;dBz(t)/dt为磁感应强度随时间的变化率(感应电动势);积分可利用高斯积分进行计算(见文献[21])。
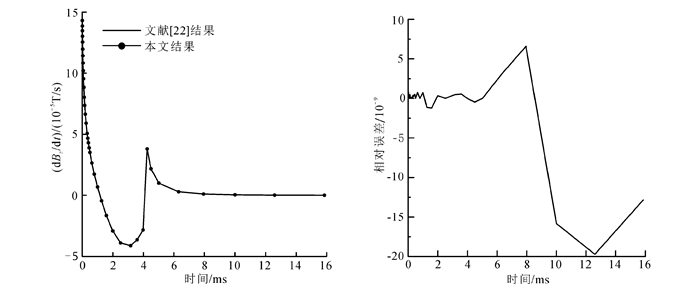
1.2 不同发射波形时间域航空电磁响应特征首先验证本文算法的可靠性。为此,假设均匀半空间模型的电阻率为1Ω·m,相对磁导率和相对介电常数均为1。h=30 m,d=50 m,r=10 m,发射偶极矩为615 000 A·m2。我们以半正弦波为例进行时间域航空电磁响应计算的精度验证,结果如图 2所示,吻合程度令人满意;对于梯形波和三角波,我们可得到类似结论。限于篇幅,这里不作赘述。
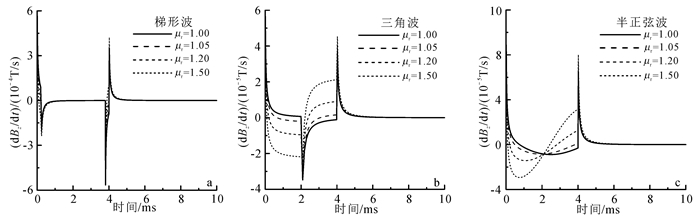
下面我们首先研究均匀半空间导电导磁介质的时间域航空电磁响应特征。航空电磁系统参数与图 2所用相同。图 3给出均匀半空间不同磁导率梯形波、三角波和半正弦波激励产生的电磁响应。均匀半空间的电阻率为10 Ω·m。梯形波的上升沿和下降沿持续时间为0.2 ms,稳定时间为3.6 ms;三角波的上升沿和下降沿均为2.0 ms;半正弦波持续时间为4.0 ms;基频均为30 Hz。
|
| 图 3 发射波形为梯形波(a)、三角波(b)、半正弦波(c)时的dBz/dt响应 Figure 3 EM responses for trapezoid (a), triangular (b) and half-sine (c) transmitting wave |
|
|
由图 3可以看出,不论供电时还是断电后的dBz/dt响应,其幅值都随着磁导率的增大而增大,而且供电时的幅值变化比断电后更加明显。比较不同发射波形供电时的电磁响应可以发现,发射波形为梯形波时,只有其上升沿和下降沿的电磁响应受磁导率的影响较大,在电流稳定阶段响应受磁导率的影响较小;当发射波形为三角波或半正弦波时,由于电流是不断变化的,整个供电段受磁导率的影响都比较明显。因此,在高磁性地区,要获得较为理想的电性反演结果,用三角波或半正弦波激励具有较明显的优势。如果能测得供电时的dBz/dt响应,将其与断电后响应结合起来进行全时反演,能更准确地反演出大地的电性和磁性参数。基于此结论,本文提出一种全时电磁响应数据的反演方法。
2 反演理论本文以阻尼最小二乘反演方法为基础,将磁导率加入反演参数,改变雅可比矩阵以实现电阻率、磁导率和层厚的同步反演。
假设d为电磁响应数据向量,d=[d1, d2, ..., dL]T,p为模型参数向量(电阻率、磁导率、厚度),p=[p1, p2,…,pM] T,L和M分别为响应和模型参数的数量,并满足M=3N-1。对于本文的层状大地模型,模型参数和电磁响应之间的函数关系[17]为
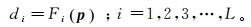 (6)
(6) 式中,F为一维非线性正演算子。首先将问题线性化,将Fi(p)在初始模型p0处展开为泰勒式并忽略高阶项得到
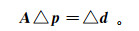 (7)
(7) 式中:△d为实际响应与初始模型响应的差值;△ p是需要求解的模型参数改正量;A为L×M的雅可比矩阵。A中各元素为
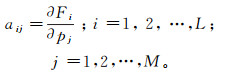 (8)
(8) 各模型参数的偏导数可以由式(1)求得。由于式(1)中与模型参数有关的变量只有rTE,因此可以先求rTE对模型参数的偏导数,即
 (9)
(9) 其中,pn为第n层的模型参数,包括电阻率、相对磁导率和层厚。
由式(2)我们可得以下递推式:
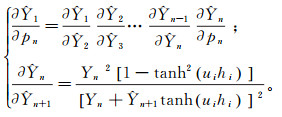 (10)
(10) 而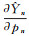
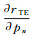
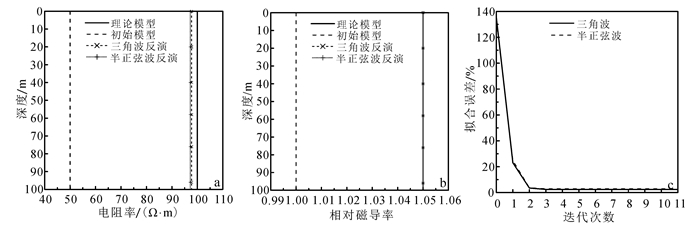
本文反演选用的系统参数如下:h=30 m,d=50 m,r=10 m,发射偶极矩为615 000 A·m2。分别以三角波和半正弦波作为发射波形,采用添加5%高斯噪声的模型正演数据进行反演。首先以磁性均匀半空间为例,电阻率为100 Ω·m,相对磁导率为1.05。利用式(1)-(5)计算全时电磁响应并添加5%高斯噪声作为反演数据。初始模型电阻率设为50 Ω·m,磁导率为自由空间的磁导率,线圈高度设为已知。反演结果如图 4所示。由图 4可以看出,对于均匀半空间模型,无论是三角波还是半正弦波激发,全时反演结果与真实模型几乎重合,各参数都能取得很好的反演结果。
|
| 图 4 均匀半空间模型的反演结果 Figure 4 Inversion results for a half-space model |
|
|
假设一个高阻磁性基底上存在一个低阻无磁性覆盖层。覆盖层电阻率为10 Ω·m,厚度为50 m;基底电阻率为150 Ω·m,相对磁导率为1.05。选择两层介质初始电阻率均为100 Ω·m,磁导率为自由空间磁导率。对ρ1,ρ2,h1和μr2的反演结果示于图 5。由图 5可以看出:三角波和半正弦波发射的反演结果都比较理想;各参数反演结果均能很好地收敛到真实模型参数,数据拟合误差在3%以下。

|
| 图 5 单个磁性层模型的反演结果 Figure 5 Inversion results for a two-layer earth model with magnetic underlying half-space |
|
|
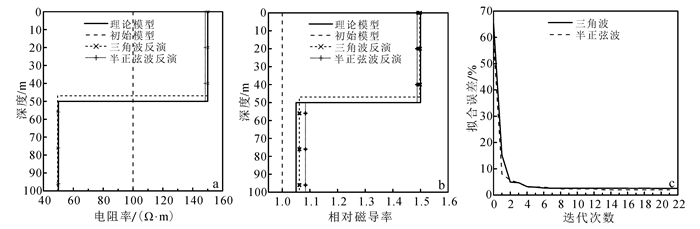
假设一个两层模型的覆盖层和基底均为磁性地层,但是具有不同的磁导率。覆盖层的电阻率为150 Ω·m,相对磁导率为1.50,厚度为50 m;基底的电阻率为50 Ω·m,相对磁导率为1.05。初始模型中各层电阻率均为100 Ω·m,磁导率为自由空间磁导率。对ρ1,ρ2,h1和μr1,μr2的反演结果如图 6所示。由图 6可见,无论是电阻率、磁导率还是层厚,经过若干次迭代后都能得到较精确的结果,拟合误差在3%以下。
|
| 图 6 两个磁性层模型的反演结果 Figure 6 Inversion results for two-layer earth model with both layers magnetic |
|
|
本文通过对不同发射波形的时间域航空电磁响应受磁导率影响的特征研究发现,不论是供电时还是断电后的dBz/dt响应,其幅值都随着磁导率的增大而增大,而且供电时的幅值变化比断电后更加明显。当发射波形为梯形波时,只有其上升沿和下降沿的电磁响应受磁导率影响较大,在电流稳定阶段响应受磁导率的影响很小;当发射波形为三角波或半正弦波时,整个供电段受磁导率的影响都比较明显。因此,在高磁性地区,用半正弦波或三角波激励能获得较为理想的地下介质电性和磁性反演结果。
通过对添加高斯噪声的时间域航空电磁理论数据反演我们发现,本文提出的全时航空电磁反演方法能有效地反演出磁性地层参数(电阻率、磁导率和层厚),可用于高磁性地区的电磁数据反演。由于供电段电磁观测目前仍存在技术问题,实测数据难以获得。因此,本文并未对实测数据进行反演,这将是我们未来的研究方向。
致谢: 裴易峰、邱长凯、黄威在本文算法和准备过程中提供了帮助,在此表示感谢。| [1] | Macnae J C, Smith R, Polzer B D. Conductivity-Depth Imaging of Airborne Electromagnetic Method in Time-Domain[J]. Geophysics, 1991, 56 (1) : 102-114. DOI:10.1190/1.1442945 |
| [2] | Liu G, Asten M. Fast Approximate Solutions of Tran-sient EM Response to a Target Buried Beneath a Conductive Overburden[J]. Geophysics, 1993, 58 (6) : 810-817. DOI:10.1190/1.1443466 |
| [3] | Wolfgram P, Karlik G. Conductivity-Depth Transform of GEOTEM Data[J]. Exploration Geophysics, 1995, 26 (3) : 179-185. DOI:10.1071/EG995179 |
| [4] | Farquharson C G, Oldenburg D W. Inversion of Time-Domain Electromagnetic Data for a Horizontally Layered Earth[J]. Geophysical Journal International, 1993, 114 (3) : 433-442. DOI:10.1111/gji.1993.114.issue-3 |
| [5] | Christiansen A V, Christensen N B. A Quantitative Appraisal of Airborne and Ground-Based Transient Electromagnetic (TEM) Measurements in Denmark[J]. Geophysics, 2003, 68 (2) : 523-534. DOI:10.1190/1.1567220 |
| [6] | Raiche A P, Jupp D L B, Rutter H, et al. The Joint Use of Coincident Loop Transient Electromagnetic and Schlumberger Sounding to Resolve Layered Structures[J]. Geophysics, 1985, 50 (10) : 1618-1627. DOI:10.1190/1.1441851 |
| [7] | Huang H, Palacky G J. Damped Least-Squares Inver-sion of Time-Domain Airborne EM Data Based on Singular Value Decomposition[J]. Geophysical Prospecting, 1991, 39 (6) : 827-844. DOI:10.1111/gpr.1991.39.issue-6 |
| [8] | 李永兴, 强建科, 汤井田. 航空瞬变电磁法一维正反演研究[J]. 地球物理学报, 2010, 53 (3) : 751-759. Li Yongxing, Qiang Jianke, Tang Jingtian. A Research on 1-D Forward and Inverse Airborne Transient Electromagnetic Method[J]. Chinese Journal of Geophysics, 2010, 53 (3) : 751-759. |
| [9] | 朱凯光, 林君, 韩悦慧, 等. 基于神经网络的时间域直升机电磁数据电导率深度成像[J]. 地球物理学报, 2010, 53 (3) : 743-750. Zhu Kaiguang, Lin Jun, Han Yuehui, et al. Research on Conductivity Depth Imaging of Time-Domain Helicopter-Borne Electromagnetic Data Based on Neural Network[J]. Chinese Journal of Geophysics, 2010, 53 (3) : 743-750. |
| [10] | 毛立峰, 王绪本, 陈斌. 直升机航空瞬变电磁自适应正则化一维反演方法研究[J]. 地球物理学进展, 2011, 26 (1) : 300-305. Mao Lifeng, Wang Xuben, Chen Bin. Study on an Adaptive Regularized 1D Inversion Method of Helicopter TEM Data[J]. Progress in Geophysics, 2011, 26 (1) : 300-305. |
| [11] | Thomas L. Electromagnetic Sounding with Suscepp-tibility Among the Model Parameters[J]. Geophysics, 1975, 42 (1) : 92-96. |
| [12] | Beard L P, Nyquist J E. Simultaneous Inversion of Airborne Electromagnetic Data for Resistivity and Magnetic Permeability[J]. Geophysics, 1998, 63 (5) : 1556-1564. DOI:10.1190/1.1444452 |
| [13] | Telford W M, Geldart L P, Sheriff R E. Applied Geophysics2nd ed [M]. Cambridge: Cambridge University Press, 1990 . |
| [14] | Zhang Z, Oldenburg D W. Recovering Magnetic Su-sceptibility from Electromagnetic Data over a One-Dimensional Earth[J]. Geophysical Journal International, 1997, 130 (2) : 422-434. DOI:10.1111/gji.1997.130.issue-2 |
| [15] | Huang H, Fraser D C. Magnetic Permeability and Electric Resistivity Mapping with a Multifrequency Airborne EM System[J]. Exploration and Geophysics, 1998, 29 (2) : 249-253. DOI:10.1071/EG998249 |
| [16] | Zhang Z, Oldenburg D W. Simultaneous Recons-truction of 1-D Susceptibility and Conductivity from Electromagnetic Data[J]. Geophysics, 1999, 64 (1) : 33-47. DOI:10.1190/1.1444528 |
| [17] | Huang H, Fraser D C. Inversion of Helicopter Ele-ctromagnetic Data to a Magnetic Conductive Layered Earth[J]. Geophysics, 2003, 68 (4) : 1211-1223. DOI:10.1190/1.1598113 |
| [18] | 覃庆炎, 王绪本, 毛立峰. 导电导磁层状介质上的固定翼航空瞬变电磁响应[J]. 地球物理学进展, 2011, 26 (5) : 1796-1801. Qin Qingyan, Wang Xuben, Mao Lifeng. The Fixed-Wing Airborne Transient Electromagnetic Response of a Magnetic Conductive Layered Medium[J]. Progress in Geophysics, 2011, 26 (5) : 1796-1801. |
| [19] | 殷长春, 邱长凯, 刘云鹤, 等. 时间域航空电磁数据加权横向约束反演[J]. 吉林大学学报(地球科学版), 2016, 46 (1) : 254-261. Yin Changchun, Qiu Changkai, Liu Yunhe, et al. Weighted Laterally-Constrained Inversion of Time-Domain Airborne Electromagnetic Data[J]. Journal of Jilin University (Earth Science Edition), 2016, 46 (1) : 254-261. |
| [20] | Nabighian M N. Electromagnetic Methods in Applied Geophysics [M]. Tulsa: Society of Exploration Geophysicists, 1988 . |
| [21] | 殷长春, 黄威, 贲放. 时间域航空电磁系统瞬变全时响应正演模拟[J]. 地球物理学报, 2013, 56 (9) : 3153-3162. Yin Changchun, Huang Wei, Ben Fang. The Full-Time Electromagnetic Modeling for Time-Domain Airborne Electromagnetic Systems[J]. Chinese Journal of Geophysics, 2013, 56 (9) : 3153-3162. |
| [22] | Yin C, Smith R S, Hodges G, et al. Modeling Re-sults of On-and Off-Time B and db/dt for Time-Domain Airborne EM Systems[C]//70th EAGE Conference and Exhibition Incorporating SPE EUROPEC 2008. Rome:[s. n.], 2008:1-4. |
| [23] | Yin C. Geoelectrical Inversion for a One-Dimensional Anisotropic Model and Inherent Non-Uniqueness[J]. Geophysical Journal International, 2000, 140 (1) : 11-23. DOI:10.1046/j.1365-246x.2000.00974.x |