2. 河海大学地球科学与工程学院, 南京 210098
2. School of Earth Science and Engineering, Hohai University, Nanjing 210098, China
0 引言
发展地源热泵技术是节能减排、建设资源节约型和环境友好型社会的迫切需求,也是改变我国传统能源利用结构的有效途径。与其他地源热泵相比,地下水源热泵(GWHPs)是目前空调系统中能效比(COP)最高的制冷、制热方式,理论计算值可达到7,实际运行值为4~6;因其节能效果显著、运行成本低和环境友好等优点而倍受大家的青睐。其原理是利用含水层浅层地热能温度常年保持稳定的特点,采用热泵技术,通过输入少量的高品位电能,将地下水中低品位难以利用的热能(冷能)提取出来,实现为建筑物供热(制冷)的过程[1]。但由于技术上的不完善,在工程应用中暴露了一系列问题,使得此项技术在我国现阶段面临机遇与挑战并存的局面。地下水源热泵的最大特点就是对地下水的抽、灌循环利用。地下水作为国家的战略资源,与老百姓的生产生活密切相关,如果不能将100%符合标准的热泵尾水回灌于同一抽水含水层内,那么将会带来一系列的生态环境问题,这已经成为制约地下水回路系统的主要技术“瓶颈”;因此,地下水回灌是不可避免和忽视的问题,它几乎成为地下水源热泵技术成败的基石。地源热泵技术的成功应用,使得近乎无限的太阳能或地能的有效应用成为现实,该项技术将会成为21世纪最有效的供热和制冷空调技术。回灌与抽水的不同点在于它不仅涉及渗流力学,还涉到物理、化学、生物等一系列交叉学科,主要表现为:在回灌过程中,回灌水中往往携带固体悬浮物、细菌、气泡、土体颗粒等,它们势必会沿着水流方向在回灌井周围含水层内发生物理沉淀和化学、生物作用从而产生堵塞,导致含水层渗透能力降低。
国外开展回灌堵塞问题机理研究已经有很长的历史,而国内研究相对较晚,研究内容主要涉及含水层颗粒物物理堵塞[2-7]、化学作用堵塞[8-9]、微生物堵塞[10-13]以及同时考虑这三种堵塞作用的实验及模型研究[14]。在大量研究成果的基础上,人们已经意识到物理、化学堵塞作用的严重性,在回灌过程中制定了一系列标准和工程应对措施,大大缓解了堵塞程度。但是,存在的物理、化学堵塞并不能随水处理和注水技术的提高而完全消除;微生物的生长代谢作用是仅次于颗粒物堵塞作用的第二大堵塞问题[15],其危害性最大,可能形成永久性堵塞[16]。试验表明,灭菌措施能够获得较为理想的效果,但是在高营养环境中少量细菌也能表现出再生长的能力。因此,虽然含水层回灌过程中的堵塞作用可以通过人为干预得到缓解,但是无法完全消除,这种情况下,对于含水层堵塞程度的评价显得很有必要,它可以为回灌工程设计提供依据。
目前也存在一些方法来预测含水层潜在的堵塞程度,包括利用修正的结垢指数[17]、生物降解的有机碳含量[18]等指标以及一些数学经验和分析模型[19]等进行预测;但其不足之处在于,这些方法往往是比较单一地针对某一项堵塞指标进行预测,无法实现对物理机械作用、化学、生物堵塞作用的整体评估,因而不能对含水层系统回灌周期内的回灌能力进行动态描述。本文引入暂时性堵塞率与永久性堵塞率的概念,将堵塞的物理过程进行区分,推导了考虑堵塞条件下含水层回灌与回扬物理过程中压力变化的解析解,获得回灌与回扬过程中灌压随时间变化的规律。工程应用中,可以利用实测数据计算含水层的堵塞率以及永久堵塞在整体堵塞中所占的比例,对回灌井的堵塞情况作出评价;也可以实现利用实验判断不同成分的回灌水源对含水层堵塞的机理分析,从而能够达到科学制定回灌水源标准的目的。
1 渗透系数模型地下水回灌物理过程中,以回灌井轴为中心,在含水层不同位置处,堵塞作用导致渗透系数不断减小;因此,渗透系数不变已经不能够真实地反映井内压强(灌压)(注:文章中接下来都以灌压来表示井内压强)变化的水力学特性。如果假定渗透系数为定值,那么对含水层内温度场的预测也将会造成影响。何满潮等[20-21]利用天津市地热单井回灌试验给出了渗透系数的衰减模型。倪龙等[22]在此基础上考虑回扬,假定回扬措施结束后渗透系数便恢复到初始状态,且不考虑回扬时间;当然,这一改变对于回扬的效果给出了很好的数学描述,但是该研究并没有考虑回扬过程中渗透系数变化的真实物理过程,因为回扬对永久堵塞问题是难以解决的。本文将永久堵塞问题考虑到渗透系数衰减的解析解推导过程中,得到了不同回扬次数渗透系数的解析表达式,将其应用于Theis公式,获得了考虑渗透系数衰减以及暂时性堵塞率条件下回灌与回扬物理过程中含水层压强的解析表达式,更准确地刻画了回灌与回扬的真实物理过程。
将渗透系数K表示为时间τ的函数,K=K0(τ),在回灌过程中,其表达式满足一级反应动力学方程[20-21]:
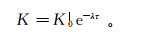 (1)
(1) 其中:K为渗透系数,m/s;τ为时间,s;K0为渗透系数的初始值,m/s;λ为渗透系数的衰减系数,h-1,它是一个与物理、化学及生物堵塞程度有关的物理量。
2 回灌与回扬过程解析解推导目前,在涉及地下水源热泵工程的回灌技术中,针对井管自身的堵塞问题往往可以通过洗井、酸化、更换井管等方法来缓解和消除;然而,回灌井周围含水层一旦堵塞,这些方法将难以生效。研究表明,回灌过程中渗透系数的衰减及微生物群落的变化大多集中于距离回灌井位置较近处[7, 11, 23-24],采用定期回扬[6, 25]的方法对于缓解含水层机械性堵塞是一个行之有效的方法。因此,本文对回灌与回扬过程中渗透系数的变化进行了数学描述。首先,将回灌所引起的堵塞分为两个部分:一部分是由于物理作用形成的暂时性堵塞,它可以通过回扬措施恢复渗透性,设其所占的比例为S;另一部分是由于化学反应和微生物生长代谢作用形成的永久性堵塞,它无法通过回扬措施来解决,设其所占的比例为F。那么,定义暂时性堵塞率δ为
 (2)
(2) 假设回灌过程中含水层的衰减系数为λ,第一次回灌时含水层初始渗透系数为K01,回灌持续时间为τ1,回扬时间为τ′1,根据式(1),可以得到第一次回灌结束后的渗透系数K1为
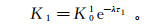 (3)
(3) 那么,第一次回灌结束后渗透系数的变化量ΔK1表示为
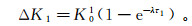 (4)
(4) 在渗透系数的变化量中,依据暂时性堵塞率δ的定义,第一次回扬措施实施后,渗透系数的恢复量Kr1可以表示为
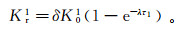 (5)
(5) 此时,第二次回灌时初始渗透系数K02可以用第一次回灌结束的渗透系数与回扬措施结束后渗透系数的恢复量之和表示:
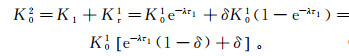 (6)
(6) 同理,第二次回灌结束时的渗透系数K2为
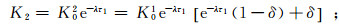 (7)
(7) 第二次回灌结束后渗透系数的变化量ΔK2为
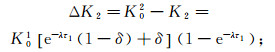 (8)
(8) 采取第二次回扬措施后,渗透系数的恢复量Kr2可以表示为
 (9)
(9) 第三次回灌时初始渗透系数K03可以表示为
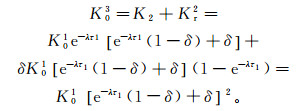 (10)
(10) 同理,第三次回灌结束时的渗透系数K3为
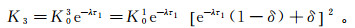 (11)
(11) 以此类推,可以得到渗透系数衰减条件下,不同回扬次数的渗透系数解析表达式。根据回灌周期的长短,在回灌第n次前,回灌的初始渗透系数Kn0的解析表达式为
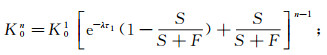 (12)
(12) 回灌第n次后的渗透系数Kn的表达式为
 (13)
(13) 那么,如果回灌过程中含水层水流满足Theis公式的假设条件,则可以推导出渗透系数衰减条件下,针对不同回扬次数灌压随时间的变化规律。Theis公式的解析式[26]可以表示为
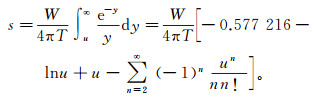 (14)
(14) 其中:s为含水层内任意一点处的降深,m;W为回灌流量,m3/d;W(u)为井函数,u为井函数变量,u=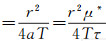
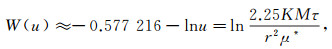 (15)
(15) 式中,M为含水层厚度,m。将式(15)代入式(14)可得
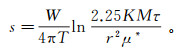 (16)
(16) 式中,r为井径,m。水位降深s可写为
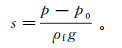 (17)
(17) 式中:p0为含水层的初始压强,MPa;p为井内灌压,MPa;ρf为水的密度,kg/m3;g为重力加速度, m/s2。
将式(17)代入式(16)可得
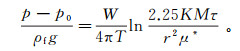 (18)
(18) 将式(13)代入式(18)并整理,得到满足Theis井流条件下考虑渗透系数衰减以及暂时性堵塞率条件下回灌与回扬物理过程中含水层压强的解析表达式:

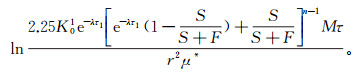 (19)
(19) 为了研究连续回灌不回扬与回扬两种情况下灌压随时间的变化特征,选取了以井轴为中心,半径为10 km的承压含水层单井回灌区域为研究对象进行研究。含水层厚度为100 m,井半径为0.15 m,完整井,计算时间为100 d。我们知道,每次回灌结束后含水层水位都有一个上升值。本文通过计算得知,以最大回灌量回灌100 d可以使整个含水层系统压强升高0.001 MPa,这个水位的变化相对于井内灌压来说是可以忽略的;因此,为了讨论方便,文中假设每次回扬都恢复到第一次回灌前的原始水位。另外,计算中暂时不考虑回扬时间。在如表 1所示的计算参数下,计算了连续回灌不回扬和回扬(不同回扬次数)在两种工况条件下灌压随时间的变化规律。模型示意图如图 1所示,两种工况的计算参数见表 2。
| p0/ MPa |
r/ m |
ρf/ (kg/m3) |
K/ (m/s) |
M/ m |
W/ (m3/d) |
λ/ h-1 |
μs/ (1/m) |
| 1.013 | 0.15 | 1×103 | 1×10-4 | 100 | 360 | 0.001 | 1×10-5 |
| 注:μs为储水率。 | |||||||

|
| 图 1 模型示意图 Figure 1 Schematic diagram of model |
|
|
| f | W/(m3/d) | δ | |
| 工况Ⅰ | 0, 1, 4, 9 | 600 | 0.9 |
| 工况Ⅱ | 0, 4 | 600, 800, 1 000, 1 200 | 0.9 |
| 工况Ⅲ | 0, 1, 4, 9 | 600, 800, 1 000, 1 200 | 1, 0.9, 0.8, 0.7, 0.6 |
| 注:f为回扬次数;W为回灌流量;δ为暂时性堵塞率。 | |||
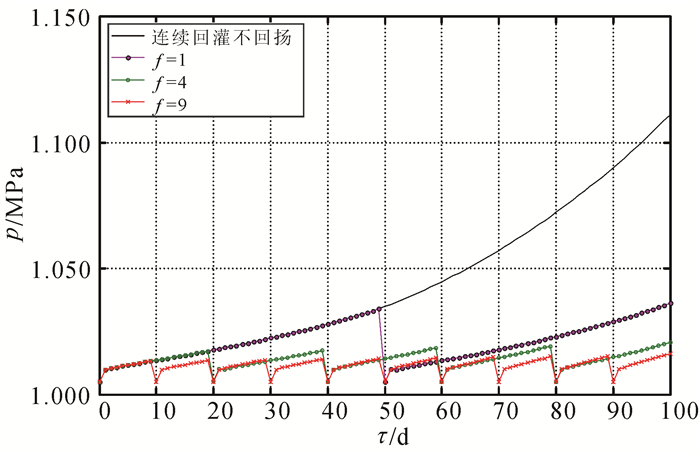
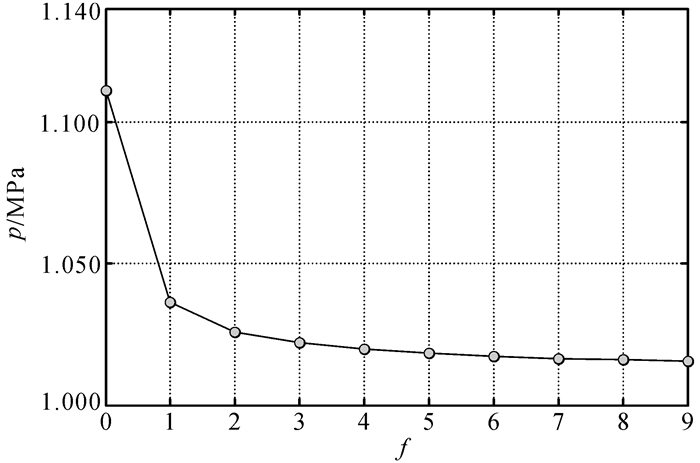
在工况Ⅰ条件下,即回灌流量W=600 m3/d、暂时性堵塞率δ=0.9,连续回灌不回扬与回扬(回扬次数为f)时灌压随时间的变化规律计算结果见图 2。在连续回灌不回扬过程中,含水层内渗透系数衰减满足一级反应动力学表达式,井内灌压增长符合指数曲线变化特征,灌压从初始的1.013 MPa升高至1.111 MPa。而采取回扬措施后,含水层内渗透系数衰减满足本文推导的解析解,它完全改变了井内原有的压强变化规律,由指数连续上升转变为间断式阶梯上升;随着渗透系数的恢复,井内灌压得到了有效降低,回扬次数为1、4、9时,回灌周期结束时灌压分别减少为1.036、1.020、1.016 MPa,仅为原灌压上升量的23.47%、7.14%、3.06%。图 3给出了井内灌压随回扬次数的变化曲线,可以看出,回扬次数越多,灌压下降得越明显。但是,考虑到回灌的经济效益以及回灌的效率问题,并不是回扬次数越多越好,因为随着回扬次数的递增,灌压的减小率越来越小,因此,根据工程实际选择合适回扬次数能够有效地缓解回灌困难问题。
|
| W=600 m3/d, δ=0.9。 图 2 灌压随时间的变化规律 Figure 2 Changing principles of injection pressure with time |
|
|
|
| 图 3 灌压随回扬次数的变化曲线 Figure 3 Changing curve of injection pressure with periodic backwashing times |
|
|
工况Ⅰ在计算时选取了暂时性堵塞率为0.9,以回扬1次的结果为例:第一次回灌结束时灌压为1.034 MPa;而在第二次回灌结束时灌压升为1.036 MPa,增加了0.002 MPa。这是由于考虑了永久堵塞率问题,从而对回扬效率产生了影响。这表明本文推导的解析解能够很好地反映这一客观存在的物理过程。
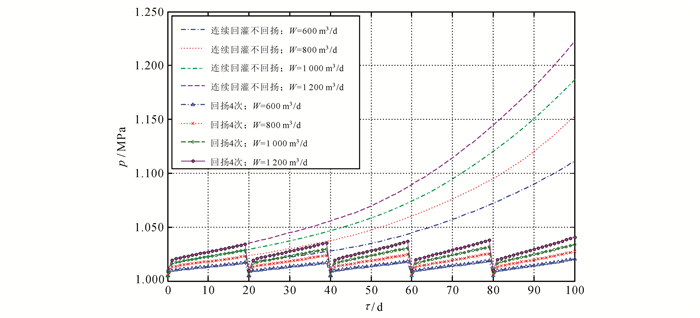
3.3 工况Ⅱ灌压变化规律在工况Ⅱ条件下,即暂时性堵塞率δ=0.9时,连续回灌不回扬与回扬在不同回灌流量下灌压随时间的变化规律计算结果见图 4。对比连续回灌不回扬的4条曲线可知,流量对灌压的影响是显著的,随着回灌流量的增大,井内的灌压也随之增大;在含水层渗透能力一定的条件下,如果相同时间需要灌入更多的水,那么必须采取加压回灌。回扬措施的实施在很大程度上减小了灌压,并且在不同流量条件下与回灌不回扬存在类似的规律。因此,在能保证100%回灌的情况下,采用小流量回灌方式能够取得较好的回灌效果,尽量避免加压回灌对井管造成破坏。
|
| δ=0.9。 图 4 不同回灌流量条件下灌压随时间的变化规律 Figure 4 Changing laws of the injection pressure with time under different injection flow |
|
|
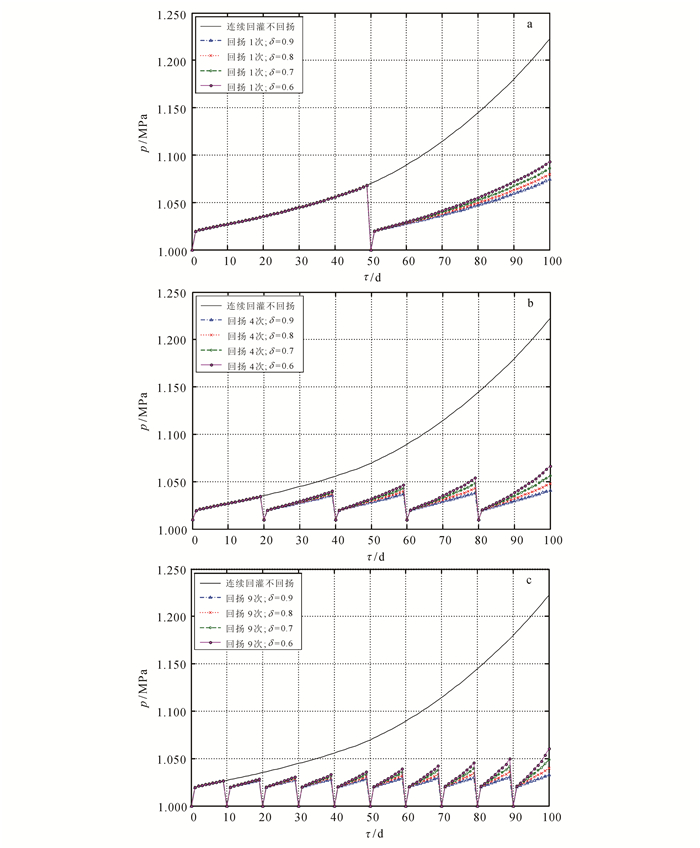
根据工况Ⅲ计算结果,图 5描述了回灌流量W=1 200 m3/d、不同回扬次数和不同暂时堵塞率条件下灌压随时间的变化规律。从图 5回扬1次过程来看,解析解精确计算了不同暂时堵塞率条件下回扬过程灌压的变化规律:暂时堵塞率越大,灌压随时间上升越缓,回扬效率越好。回灌结束后4种暂时堵塞率对应的灌压如表 3所示。
| δ | p/MPa | △p/MPa | |||||
| f=1 | f=4 | f=9 | f=1 | f=4 | f=9 | ||
| 1.0 | 1.068 | 1.034 | 1.026 | 0.000 | 0.000 | 0.000 | |
| 0.9 | 1.074 | 1.041 | 1.033 | 0.006 | 0.007 | 0.007 | |
| 0.8 | 1.080 | 1.048 | 1.040 | 0.012 | 0.014 | 0.014 | |
| 0.7 | 1.086 | 1.056 | 1.049 | 0.018 | 0.022 | 0.023 | |
| 0.6 | 1.093 | 1.066 | 1.060 | 0.025 | 0.032 | 0.034 | |
| 注:δ为0.9,0.8,0.7,0.6时为考虑永久堵塞工况;δ为1.0时为不考虑永久堵塞工况。W=1 200 m3/d。 | |||||||
|
| W=1 200 m3/d。 图 5 不同暂时性堵塞率条件下灌压随时间的变化规律 Figure 5 Changing laws of the injection pressure with time under different temporary plugging rates |
|
|
表 3表明,回扬1次时:如果不考虑永久堵塞作用,回灌结束的灌压为1.068 MPa;4种暂时性堵塞率条件下,灌压误差范围为0.006~0.025 MPa, 转化为井内水头达到了0.6~2.5 m。这个误差是不容忽视的,回灌过程中如何有效地控制永久性堵塞是控制灌压误差的关键。从表 3还可以看出:灌压误差随回扬次数的增加而逐渐增大,其中,当回扬9次时,最大的灌压误差已经达到了0.034 MPa;但增加幅度逐渐变缓,而且误差随着暂时堵塞率的减小而增大。
通过解析解对暂时堵塞率与永久堵塞率在回灌与回扬过程中的刻画,清晰地描述了堵塞的物理过程,能够使我们掌握含水层的堵塞性质,也为地下水回灌工程应用提供了理论依据。
4 结论与建议1)本文在渗透系数衰减模型基础上,提出了暂时性堵塞率的概念,结合Theis公式,获得了考虑渗透系数衰减以及暂时性堵塞率条件下回灌与回扬物理过程中含水层压强的解析表达式,准确地刻画了回灌与回扬物理过程,为地下水回灌工程应用提供了理论依据。
2)不同工况的计算结果揭示了回灌过程中灌压的变化规律。连续回灌不回扬,井内灌压增长符合指数曲线变化特征;采取回扬措施后,变化规律由满足指数的连续上升转变为间断式阶梯上升,回扬次数越多,灌压下降越明显。但是,灌压的递减率随着回扬次数增加而降低,因此,缓解回灌困难时,在考虑回扬措施的同时仍需关注回扬次数。
3)地下水回灌过程中,灌压误差与回扬次数、永久性堵塞率呈正相关,在工程设计中,相关影响因素不可忽略。以后的实验中建议采用标准粒径玻璃微珠介质模拟含水层来开展物理模型试验,依据两种堵塞率的结果来分析不同成分回灌水源对含水层的堵塞机理,以达到科学制定回灌水源标准的目的。
| [1] | 周彦章, 周志芳, 吴蓉, 等. 地源热泵系统地下水热量运移阶段特性模拟研究[J]. 水文地质工程地质, 2011, 38 (5) : 128-134. Zhou Yanzhang, Zhou Zhifang, Wu Rong, et al. Simulation Study of the Stage-Characteristics of Groundwater Thermal Transport in Aquifer Medium for GWHP System[J]. Hydrogeology & Engineering Geology, 2011, 38 (5) : 128-134. |
| [2] | Silliman S E. The Importance of the Third Dimension on Transport Through Saturated Porous Media: Case Study Based on Transport of Particles[J]. Journal of Hydrology, 1996, 179 (1) : 181-195. |
| [3] | Silliman S E. Particle Transport Through Two-Dimen-sional, Saturated Porous Media: Influence of Physical Structure of the Medium[J]. Journal of Hydrology, 1995, 167 (1) : 79-98. |
| [4] | 赵军, 刘泉声, 张程远. 水源热泵回灌困难颗粒阻塞试验研究[J]. 岩石力学与工程学报, 2012, 31 (3) : 604-609. Zhao Jun, Liu Quansheng, Zhang Chengyuan. Experimental Study of Particles Clogging in Ground Source Heat Pump[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31 (3) : 604-609. |
| [5] | 黄修东, 束龙仓, 刘佩贵, 等. 注水井回灌过程中堵塞问题的试验研究[J]. 水利学报, 2009, 40 (4) : 430-434. Huang Xiudong, Shu Longcang, Liu Peigui, et al. Experimental Study on Injection Wells During the Clogging of Recharge[J]. Hydraulic Engineering, 2009, 40 (4) : 430-434. |
| [6] | 赵忠仁. 回灌井暂时性堵塞物的形成及其排除过程变化机制分析[J]. 水文地质工程地质, 1988, 11 (5) : 39-42. Zhao Zhongreng. Mechanism of the Formation of a Temporary Blockage of Recharge Wells and Exclude the Change Process[J]. Hydrogeology & Engineering Geology, 1988, 11 (5) : 39-42. |
| [7] | 路莹, 杜新强, 迟宝明, 等. 地下水人工回灌过程中多孔介质悬浮物堵塞实验[J]. 吉林大学学报(地球科学版), 2011, 41 (2) : 448-454. Lu Ying, Du Xinqiang, Chi Baoming, et al. The Porous Media Clogging due to Suspended Solid During the Artificial Recharge of Groundwater[J]. Journal of Jilin University (Earth Science Edition), 2011, 41 (2) : 448-454. |
| [8] | Santos A, Bedrikovetsky P. A Stochastic Model for Particulate Suspension Flow in Porous Media[J]. Transport in Porous Media, 2006, 62 (1) : 23-53. DOI:10.1007/s11242-005-5175-7 |
| [9] | Weroński P, Walz J Y, Elimelech M. Effect of De-pletion Interactions on Transport of Colloidal Particles in Porous Media[J]. Journal of Colloid and Interface Science, 2003, 262 (2) : 372-383. DOI:10.1016/S0021-9797(03)00174-7 |
| [10] | 姜桂华, 廖资生, 徐凌云, 等. 人工微生物脱氮过程中含水层堵塞问题的实验研究[J]. 长春科技大学学报, 1998, 28 (2) : 186-190. Jiang Guihua, Liao Zisheng, Xu Lingyun, et al. The Experimental Study on Clogging of Aquifer During the Treatment of Nitric Pollution by Syntheticmicroor Ganism[J]. Journal of Changchun Universsity of Science and Technology, 1998, 28 (2) : 186-190. |
| [11] | 路莹, 杜新强, 范伟, 等. 地下水人工回灌过程中微生物堵塞的预测[J]. 湖南大学学报(自然科学版), 2012, 39 (1) : 77-80. Lu Ying, Du Xiniang, Fan Wei, et al. Prediction of Microbial Clogging in Groundwater Artificial Recharge[J]. Journal of Hunan University (Natural Sciences), 2012, 39 (1) : 77-80. |
| [12] | Baveye P, Vandevivere P, Hoyle B L, et al. En-vironmental Impact and Mechanisms of the Biological Clogging of Saturated Soils and Aquifer Materials[J]. Critical Reviews in Environmental Science and Technology, 1998, 28 (2) : 123-191. DOI:10.1080/10643389891254197 |
| [13] | Hoffmann A, Gunkel G. Bank Filtration in the Sandy Littoral Zone of Lake Tegel (Berlin): Structure and Dynamics of the Biological Active Filter Zone and Clogging Processes[J]. Limnologica-Ecology and Management of Inland Waters, 2011, 41 (1) : 10-19. DOI:10.1016/j.limno.2009.12.003 |
| [14] | Rinck-Pfeiffer S, Ragusa S, Sztajnbok P, et al. In-terrelationships Between Biological, Chemical, and Physical Processes as an Analog to Clogging in Aquifer Storage and Recovery (Asr) Wells[J]. Water Research, 2000, 34 (7) : 2110-2118. DOI:10.1016/S0043-1354(99)00356-5 |
| [15] | Oberdorfer J A, Peterson F L. Waste‐Water In-jection: Geochemical and Biogeochemical Clogging Processes[J]. Ground Water, 1985, 23 (6) : 753-761. DOI:10.1111/gwat.1985.23.issue-6 |
| [16] | Vigneswaran S, Suazo R B. A Detailed Investigation of Physical and Biological Clogging During Artificial Recharge[J]. Water, Air, and Soil Pollution, 1987, 35 (1/2) : 119-140. |
| [17] | Hutchinson A S. Estimation and Quantification of In-jection Well Clogging, Tucson, Arizona[J]. Estimation & Quantification of Injection Well Clogging Tucson Arizona, 1993, 23 (2) : 34-45. |
| [18] | Pavelic P, Dillon P J, Barry K E, et al. Water Qua-lity Effects on Clogging Rates During Reclaimed Water Asr in a Carbonate Aquifer[J]. Journal of Hydrology, 2007, 334 (1) : 1-16. |
| [19] | Vandevivere P, Baveye P, Lozada D S, et al. Mic-robial Clogging of Saturated Soils and Aquifer Materials: Evaluation of Mathematical Models[J]. Water Resources Research, 1995, 31 (9) : 2173-2180. DOI:10.1029/95WR01568 |
| [20] | 何满潮, 刘斌, 姚磊华, 等. 地热单井回灌渗流场理论研究[J]. 太阳能学报, 2003, 24 (2) : 197-200. He Manchao, Liu Bin, Yao Leihua, et al. Study on the Theory of Seepage Field for Geothermal Single Well Reinjectong[J]. Acta Energiae Solaris Sinica, 2003, 24 (2) : 197-200. |
| [21] | 何满潮, 刘斌, 姚磊华, 等. 地下热水回灌过程中渗透系数研究[J]. 吉林大学学报(地球科学版), 2002, 32 (4) : 374-377. He Manchao, Liu Bin, Yao Leihua, et al. Study on Hydraulic Conductivity During Geothermal Reinjection[J]. Journal of Jilin University (Earth Science Edition), 2002, 32 (4) : 374-377. |
| [22] | 倪龙, 马最良. 地下水地源热泵回灌分析[J]. 暖通空调, 2006, 36 (6) : 84-90. Ni Long, Ma Zuiliang. Analysis of Injection for Groundwater Source Heat Pump Systems[J]. Journal of HV&AC, 2006, 36 (6) : 84-90. |
| [23] | 李璐, 卢文喜, 杜新强, 等. 人工回灌过程中含水层堵塞试验研究[J]. 人民黄河, 2010, 32 (6) : 77-78. Li Lu, Lu Wenxi, Du Xinqiang, et al. Artificial Aquifer Recharge Process Blockage Experimental Research[J]. Yellow River, 2010, 32 (6) : 77-78. |
| [24] | 苏小四, 孟祥菲, 张文静, 等. 人工回灌过程中地下水微生物群落变化[J]. 吉林大学学报(地球科学版), 2015, 45 (2) : 573-583. Su Xiaosi, Meng Xiangfei, Zhang Wenjing, et al. Change of the Groundwater Microbial Community During Artificial Recharge Process[J]. Journal of Jilin University (Earth Science Edition), 2015, 45 (2) : 573-583. |
| [25] | 孙美华, 张金霞, 魏建中. 地下水源热泵重力回灌的回扬实验研究[J]. 煤气与热力, 2009, 29 (8) : 1-4. Sun Meihua, Zhang Jinxia, Wei Jianzhong. Experimental Research on Pump Lifting from Gravity Artificial Recharge Well of Underground Water Source Heat Pump System[J]. Gas&Heat, 2009, 29 (8) : 1-4. |
| [26] | 陈崇希, 林敏. 地下水动力学 [M]. 武汉: 中国地质大学出版社, 1999 . Chen Chongxi, Lin Min. Groundwater Dynamics [M]. Wuhan: China University of Geosciences Press, 1999 . |


