0 引言
高频渐近散射理论指的是以高频渐近分析(高频近似)为基础的散射理论,其基本任务是在高频或短波长条件下给出相应散射问题的解析或半解析解,其经典内容是渐近几何射线级数理论和Kirchhoff积分理论,以及基于这两个理论所提出的几何绕射理论和物理绕射理论[1-10]。
在字面上,几何射线级数理论是短语theory of asymptotic ray series的中文翻译;Kirchhoff积分理论是短语Kirchhoff integral theory的中文翻译;几何绕射理论是短语geometrical theory of diffraction的中文翻译;物理绕射理论是短语physical theory of diffraction的中文翻译[11-12]。
在物理上,几何射线级数的首项描述几何光学场(geometrical optics field,或称为Sommerfeld-Runge试探解(Sommerfeld-Runge ansaz))[1, 8-10],高阶项描述沿几何射线方向的散射场,即前向散射或透射场[13]。在文献中,基于几何光学场的射线理论被称为零阶射线理论(zero-order ray theory)或零阶渐近射线理论(zero-order asymptotic ray theory,简称为ART)[10]。Kirchhoff积分描述孔径绕射场,由此而发展起来的绕射理论称为Kirchhoff绕射理论[1, 4-5, 7, 9]。几何绕射理论描述边缘和表面绕射场,简称为GTD或Keller理论[8, 11-12]。物理绕射理论描述绕射体表面的亮区对于绕射场的贡献,简称为PTD或Umfimtsev(Уфимицев)理论[11]。值得注意的是,在孔径或边缘绕射问题中,几何绕射理论和物理绕射理论,即GTD和PTD的核心公式均可由Kirchhoff绕射积分导出[1-2, 7, 11];因此,在某种程度上可以将这两种理论看作是Kirchhoff绕射理论的具体应用。另外,几何绕射理论(GTD)中的核心内容边缘绕射定律已经被有关的光学实验所证实[14]。因此,几何绕射理论不仅有坚实的数学理论基础,更有坚实的物理实验基础。
在历史上,几何射线级数理论由Luneburg在20世纪40年代提出。与常规做法不同,Luneburg不是通过科技期刊来发表他的一系列关于光学的研究成果的,这些成果是在由他主讲的、由Brown大学、New York大学等美国高校在1944—1948年间举办的一系列讲座中公布于众的[15],这些成果的载体不是科技论文,而是一系列讲义。1964年,University of California Press将这些讲义汇集成为《Mathematical Theory of Optics》一书[14]。据著名学者和光学专家Emil Wolf评价,Luneburg的这本书以及他此前的系列讲义为光学领域中的若干分支提供了完整和系统的理论基础,包括了一系列具有原创性的重大成果(They contained a highly original, thorough, and systematic account of the foundations of several branches of optics and numerous new and important results[15])。Wolf认为,Luneburg的主要贡献是将仪器光学中的两个主要数学理论分支,即几何光学和标量绕射光学(现在称为物理光学)统一到Maxwell的电磁理论框架之中。Luneburg证明,无论是几何光学还是标量绕射光学(物理光学)均可以从Maxwell方程组导出,他们均是Maxwell方程组的特解。因此,Luneburg的工作具有划时代的意义。事实上,在Luneburg之前,几何光学和物理光学在光学中是两个相互独立的分支,相互之间没有任何联系,也与Maxwell的电磁理论基本上没有关系[15]。正是由于Luneburg的工作才使几何光学和物理光学在电磁理论的框架中融为一体。1965年,Kline和Kay合作出版了专著《Electromagnetic Theory and Geometrical Optics》[6],对Luneburg的工作进行了进一步的系统化。鉴于这个事实,几何射线级数在文献中被称为Luneburg-Kline展开[2, 6, 8]。今天,几何射线级数理论已经不仅仅是联系几何光学和物理光学的纽带和桥梁,也不仅仅是电磁学中的重要组成部分,而且还是声学和弹性动力学等学科的重要组成部分,更是解释和处理天然及人工地震数据的重要理论基础之一。事实上,早在20世纪50年代,在上述学科中就出现了冠以“几何”二字的学科分支,例如几何声学和几何地震学等等[16-18],而这些分支学科的理论基础即为几何射线级数理论。
在对几何射线级数理论的众多改进中,Keller的工作尤为重要。正是Keller将几何光学的基本思想用于处理边缘绕射现象,提出了上文所提到的几何绕射理论[18]。也正是Keller,将几何射线级数理论从电磁场扩展到弹性波场,建立了几何声学的理论框架[19-20]。在当今时代,利用几何射线理论不仅能够处理传播、反射和折射问题,也能处理边缘和表面绕射问题[2, 8, 11-12]。
另外,严格的数学分析和简单的直观对比均已经证明:几何射线级数的前三项与点源的辐射场公式完全一致[15]。事实上,点源、偶极源以及偶极天线在均匀无限大介质中的严格辐射场公式均具有几何射线级数的结构,只不过是在前三项之后所有系数均为0而已。因此,可以将几何射线理论看作是均匀介质中点源场在非均匀介质中的一种推广。从这个意义上讲,几何射线级数理论不仅是一种纯粹的数学理论,也表示一种直观的物理现实。这是能够利用几何射线理论来解决一系列实际问题的根本原因所在。
与几何射线理论不同,Kirchhoff积分就是为了处理绕射问题而提出来的。在数学上,Kirchhoff积分定义在包含孔径的曲面屏上,是对Helmholz-Kirchhoff(面)积分定理施以局部平面波近似和切平面近似的结果。因此,Kirchhoff积分是对Huygen-Fresnel原理的一种近似表述(Helmholz-Kirchhoff积分定理是对Huygens-Fresnel原理的严格数学表述[1, 4, 7, 9])。
在历史上,Kirchhoff积分理论由德国理物理学家Kirchhoff于1882年提出,其对于Helmholz-Kirchhoff积分定理的近似在于采用了两个现在称之为Kirchhoff边界条件的近似边界条件,即:1)在绕射孔径上,总波场及其法向导数等于入射波场和其法向导数;2)在不透明的绕射屏背面,场恒等于0。最初,Kirchhoff绕射理论只针对标量波和均匀介质,并且只用于处理孔径绕射问题。后来,经过Kottler、Stratton以及众多其他研究者的努力,将Kirchhoff积分从标量波推广到了矢量波,从孔径绕射问题推广到一般的曲面绕射问题。最终,通过利用零阶几何射线理论和高斯波束叠加等波场高频表示来近似Green函数,将Kirchhoff积分推广到了非均匀各项同性和各向异性介质,以及多孔介质等等复杂介质[2, 7]。
今天,在宏观波动理论中,Kirchhoff积分理论经常被用于表示非均匀各向异性介质或其他复杂介质中的表面散射或绕射场。在光学中,Kirchhoff积分及其在此基础上发展起来的Fresnel近似和Franhoff近似已经构成了现代物理光学和Fourier光学中的核心内容[21]。在现代电磁场和天线理论中,根据Kirchhoff积分思想、由前苏联物理学家Umfimtsev(Уфимицев)所提出的物理绕射理论已经成为了一种重要的、描述绕射现象的高频渐近理论[2, 11]。
无论是几何射线级数理论还是Kirchhoff积分理论,其物理基础都可以归结为由前苏联物理学家Fock在1946年所提出的局部场原理,即在高频条件下,任意复杂波场的传播、散射和绕射仅仅依赖于所考虑介质的局部几何和物理属性,且与平面波场等价[2]。具体地讲,局部场原理包含下列2点:1)在高频条件下,任意复杂波场在局部均可以被近似地视为平面波场,即局部平面波场,这在文献中被称为局部平面波近似;2)在高频条件下,任意曲率半径远远大于波长的曲面在局部可以被近似为平面,从而可用其在所考虑点处的切平面所代替,这在文献中被称为切平面近似[7]。
虽然几何射线级数理论、Kirchhoff积分理论、GTD和PTD能够解决相当一部分实际问题,但是他们各自均有致命的弱点。首先,几何射线理论在焦散区等非正则区内失效,其最显著的特征是所给出的振幅为无限大[1-10]。其次,在几何射线理论中, 能量只能在射线管中传播,而不允许其在垂直于射线管壁的方向上传播。这意味着在几何射线理论中没有考虑散射现象的体积效应和绕射现象的面积效应。因此,利用几何射线理论只能描述前向和后向散射的极端情况,即透射和反射,而对于绕射必须借助于几何绕射理论来处理。但是,几何绕射理论的一个核心问题是如何求取绕射系数。这需要求出相应典则问题的分析解,而这样的解并不是总能够求到的[8, 19]。
对于Kirchhoff积分,其先天性弱点来自于面积分算子。事实上,利用面积分算子只能处理介质参数的间断面所造成的散射或绕射,因只能计算前向或反向散射,而不能在计算其中一个的同时兼顾另一个。此外,若要利用Kirchhoff积分法必须首先知道Green函数。对于均匀介质,Green函数是可以精确地求出的。但是对于非均匀介质,Green函数只能近似地给出。一般采用零阶几何射线理论即几何光学场来近似Green函数。这样一来,就限制了Kirchhoff积分的应用范围[7]。为了解决这个问题,近年来许多研究者采用高斯波束叠加近似Green函数。虽然这个改进解决了Kirchhoff积分在焦散区内失效的问题,但是却增加了数以几倍的计算量[22]。
上述几何射线级数理论和Kirchhoff积分理论的弱点使它们难以被用于解决反散射问题,尤其是难以被用于解决类似于层析成像等面向体积分布的反散射问题。因此,为了解决光学全息[1, 9]、X射线层析以及地球物理层析和速度反演等问题,在光学和地球物理中先后引入了源于量子散射理论的Born近似和源于无线电物理的Rytov近似[5, 9, 23-24]。与Kirchhhoff积分理论相同,这两种近似理论均以加权积分的形式出现,而其权函数均为Green函数。从而,与Kirchhoff积分一样,这两种方法的应用范围均受近似Green函数有效范围的制约。但是,与Kirchhoff积分是定义在介质间断面或散射体表面上不同,在Born和Rytov近似中,相应的积分是定义在散射体所占据的空间上,来自于对以体积分形式出现的波场表示定理[5, 9, 23],属于体积分算子。
此外,与Kirchhoff积分直接定义在由介质物理参数所决定的模型空间中不同,Born和Rytov近似均要求将模型空间拆分为背景空间(模型)和扰动空间(模型)两部分。在扰动空间中,介质参数在任意给定点的值要远远小于背景空间中相同位置上的介质参数值;因此,相对于背景空间来讲,扰动空间的介质物理参数值都应该很小,其被称为小扰动。与此相反,Kirchhoff积分对于其定义域两侧的介质参数反差没有任何要求。
在物理上,小扰动意味散射过程很弱,因此Born和Rytov近似均被称为是弱散射近似。如果要突破小扰动限制,可以将Born和Rytov近似作为首项而构造相应体积分方程的级数解;这样的级数分别称为Born级数和Rytov级数[9, 23]。然而,这些级数的收敛性却是一个难以证明的问题。在数学上,如果一个级数的收敛性没有得到证明,则称其为形式级数。如果用形式级数表示一个数学物理问题的解,则称该级数为相应数学物理问题的形式解。因此,在其收敛性没有得到严格证明之前,Born和Rytov级数只能算作是相应散射问题的形式解。
除了受Green函数的近似程度和小扰动的制约外,Born和Rytov近似的计算精度还受介质的拆分方式和扰动边界值(扰动在其所占据空间边界上的取值)这两个条件的制约。对于前者,实际上没有任何标准,只要满足小扰动条件即可,因此具有很大的随意性。虽然各种满足小扰动的拆分方案在理论上均是合理的,但是不同拆分方案所对应的入射场和散射场却是不同的。因此,Born和Rytov近似中的入射场和散射场并不是物理上的入射场和散射场,而是形式上的入射场和散射场。事实上,根据Born或Rytov近似所估计(计算)出来的反射场并不是真正的、能观测到的反射场,而是一种形式上的反射场。这意味着,在Born和Rytov近似中,只有总场是唯一能与观测数据相对比的场;而背景场和散射场只是计算总场的一种辅助函数,其与总场的关系与场的位函数和场本身的关系类似。此外,数值计算表明,不同介质拆分方案尽管在理论上等价,但是在计算上并不等效,即不同的拆分方案所导致的计算结果并不相同[13]。这种不相同满足数值分析或科学计算的一般原理,即不同数值分析方案在理论上等价,但是在数值上不等效。
对于后者,即对于扰动的边界值对相应近似精度的制约来自于基于体积分的表示定理。事实上,无论是基于面积分还是基于体积分的表示定理,均来自于对Green定理的应用。因此,在表示定理中同时应该包括面积分和体积分[13, 23, 25]。对于基于面积分的表示定理,其中的体积分表示场源的贡献,可以用精确或近似的方式计算出来,故只留下面积分。对于基于体积分的表示定理,扰动被作为二次场源来处理,从而只留下体积分。然而,二次场源是分布在有限空间中的,因此在将其代入到第二Green定理后会出现沿着二次场源表面的积分。只有令这个面积分为0,才能得到文献中常见的、基于体积分的波场表示定理。在数学上,若要使沿二次源表面的积分为0,当且仅当扰动的边界值为0时才有可能[13]。因此,在文献中所出现的基于体积分的波场表示定理实际上隐含着一个使扰动的边界值为0的假设。如果扰动分布在整个空间,则根据辐射条件,面积分为0[13]。然而,如果扰动分布在有限空间,则在文献中所给出的基于体积分的波场表示定理实际上隐含着一个使扰动边界值为0的窗函数。遗憾的是,这个事实在文献中并没有得到提及和关注。另外,根据Green函数理论,如果扰动分布在有限空间且具有明确的边界,则Green函数应该满足相应的内边界条件。同样,对于这一点,在文献中也没有得到提及和关注。
为解决上述介质拆分的非唯一性问题,Coates和Chapman在1991年提出了广义Born散射理论,或称为广义Born近似(generalized Born approximation)[13]。与常规Born近似一样,广义Born近似也是一种弱散射近似;但是其散射源是近似Green函数和精确Green函数之差,而不是相对于一个背景介质的扰动。因此,在广义Born近似中不存在常规Born近似理论在介质拆分上的任意性,从而也就保证了入射场和散射场在数学表现上的唯一性和物理上的客观性。此外,在广义Born近似的体积分中所包含的被积函数与速度和密度的梯度有关,从而可以直观地表示出速度梯度变化对于反射响应的影响。然而,在Coates和Chapman的广义Born近似理论中,Green函数是利用零阶几何射线理论来近似的,因此在焦散等几何射线理论的奇异区域内失效。这与常规的Born和Rytov近似完全相同。
除了上述近似理论外,在文献中还有两种处理散射问题的近似理论,分别称为拟解析近似和拟线性近似[26-30]。如果将拟解析和拟线性近似的基本思想用于解决非均匀介质中的散射问题,则可将其中的Green函数换成其高频渐近形式,进而得到相应的高频渐近解。可以证明,拟解析近似相当于二阶Born近似,而拟线性近似是对Born级数的改进。鉴于这一事实,本文将不对拟解析和拟线性近似做专门的讨论。
在外观上,Kirchhoff、Born、广义Born以及Rytov近似都是以空间褶积的形式出现的。因此,可以从不同的角度对这些积分近似进行不同的解释[27-29]。具体地讲:1)从系统理论的角度,可以将它们看成是地下复杂电磁系统或复杂声学系统的响应,而这些系统的脉冲响应或转换函数即为相应的Green函数;2)从信号处理的角度,可以将它们看作是一种空间滤波算子,而将相应的反问题视为反滤波(褶积)过程;3)从泛函分析的角度,可以将Kirchhoff、Born、广义Born以及Rytov近似积分理解成函数空间中的映射算子,其功能是将场源信号映射成为观测数据;4)从现代数学分析的角度,可以将这些近似积分视为Fourier积分算子或拟微分算子,进而可以对它们进行渐近分析或微局部分析[31-33]。
无论是几何射线理论、Kirchhoff近似积分理论,还是Born和Rytov近似积分理论,均在地球物理数值模拟和反演成像中起着举足轻重的作用。事实上,早在20世纪80年代,在地球物理中就已经形成了以零阶几何射线理论为基础的地震波数值模拟理论和技术,并成功地运用到了天然和人工地震观测数据的解释和速度反演(走时层析)之中[34-37]; 到了世纪交替之时,又出现了基于零阶几何射线理论的立体层析成像理论[38]。
类似地,以零阶几何射线理论为Green函数近似表示的Kirchhoff积分理论被广泛地用于描述反射地震观测数据和实现反向传播,并逐渐形成了一套称为Kirchhoff型偏移成像的理论体系和基于波前构建射线追踪和程函方程有限差分数值分析的快速计算技术系列。即使到了今天,即使在逆时偏移和波束偏移已经取得了很大成功并得到了广泛重视和应用的情况下,Kirchhoff型偏移仍然是常规偏移成像处理的主要方法之一,仍然起着不可替代的作用[35, 37, 39-40]。
在以Bleistein和Hubral为代表的研究者们利用Kirchhoff积分的常规形式,即Kirchhoff型积分算子取得了一系列研究和应用成就的同时[35, 37, 39],荷兰地球物理学家Berkhout从20世纪80年代起就利用Kirchhoff积分的离散形式逐渐建立起了描述反射地震数据的矩阵模型,即WRW模型,为反射地震数据的偏移、反演以及多次波消除等提供了数据模型和出发方程[40]。在电磁场散射研究中,Zhdanov将Kirchhoff-type理论拓展到复空间,建立起了一套关于Kirchhoff-type积分的解析函数理论[41]。
同样,自从它们被引入到地球物理中的那天开始,Born和Rytov近似就在地球物理数据描述和反演成像中占有不可替代的地位。事实上,Born近似是反射和透射地震绕射层析及反射地震偏移成像和全波形反演的数据表示和出发方程[42-47],而Rytov近似是波动层析和波路径偏移等方法的出发方程[48-50]。利用Born和Rytov近似,Schuster[46]、Zhan等[47]和Sun等[48]分别提出了波路径偏移和广义逆时偏移的基本概念和基本算法。同样,利用Rytov算子,Woodward等[49-50]提出了基于波动理论的反射地震层析成像理论和方法。目前,在文献中已经将由Born和Rytov近似所导出的体积分算子分别称为Born和Rytov算子,并将其广泛用于解决偏移、反偏移、反演、多次波消除等等一系列问题当中,取得了良好的效果[31-32, 49-50]。
与上述情形相反,广义Born散射理论自从在1991年发表之后并没有受到多少关注,更没有任何关于在此基础上所建立的地球物理场正反演理论的报道。
近年来,对于Kirchhoff、Born和Rytov积分本身和其应用的研究又有了新的进展[51-54],尤其是在对Green函数的数值计算方法研究上又有了长足的进展[55]。因此,为了对高频渐近散射理论进行进一步的改进和推广,有必要对其研究现状进行综合评述。同时,也有必要对其可能的发展方向和可能的改进措施进行进一步的探讨。这两点即为本文的目的所在。
在下文中,将首先对散射理论中的基本概念和基本公式进行回顾,并对一些与散射现象有关的物理概念和数学物理问题进行评述和强调。之所以进行这样的回顾和强调主要是为了澄清和建立一些基本概念,为下一步的探讨提供基础。其次,将对高频渐近散射理论及其在地球物理场数值模拟和反演成像中应用的研究历史和研究现状进行概略的介绍和评述。再次,将对近5年内笔者在高频渐近散射理论研究中所取得的一些进展进行简单的介绍。最后,将对全文进行总结并对高频渐进散射理论研究在今后的发展及其在地球物理场数值模拟和反演成像中的应用前景进行展望。
1 基本概念、基本公式以及若干评述和强调本节回顾散射理论中的一些基本概念和基本公式,并对一些与散射现象有关的物理概念和数学内涵进行评述和强调。
1.1 基本概念根据定义,散射(scattering)指的是当来自于场源的波(入射波,incident wave)投射到表面曲率较大或者不光滑的障碍体(散射体,scatter)上时,其二次辐射响应在角度域上按一定的规律作扩散分布的现象[1-5]。由于与这些二次辐射响应相对应的波不仅沿着入射波的传播方向传播,而且还沿着与入射波传播方向不同甚至相反的其他任意方向传播,所以将其称为散射波(scattered wave)[1-5]。如果散射波的传播方向与入射波的传播方向基本一致,即分布在以入射波的传播方向为中心的一定角度范围内,则称其为前向散射(forward scattering)[1-5];反之,若散射波的传播方向与入射波的传播方向基本相反,即分布在以逆着入射波传播方向为中心的一定角度范围内,则称其为后向散射或背向散射(backward scattering或back scattering)[1-5]。前向散射的极端情况是透射,后向散射的极端情况是反射;无论是透射还是反射, 均可以作为特殊的散射现象来处理。而从散射到透射和反射的过渡需要借助于高频渐近分析,主要是稳相(stationary phase)分析或最速下降(steepest-descents)分析[1, 3, 23]。
在地球物理中,前向散射主要体现为透射,包括地下到地表的透射、地表到地下靶区的透射和钻井间的透射。反向或背向散射主要是反射和漫射(没有优势传播方向的散射)。对于反射地震勘探来讲,反向散射是观测数据,而对其进行的观测、处理和解释是反射地震勘探的主体内容。
如果散射过程是一次性的,即入射波直接来自于场源,则称其为一次散射(primary scattering);反之,如果入射波来自于其他散射体,则称其为多次散射(multiple scattering)。其中,一次反射主要发生在无限大背景介质中的单体散射过程中,而多次反射一般发生在多体问题或复杂背景介质中的散射问题中。
在地球物理中,一次散射主要是反射和透射,而多次散射形成所谓的多次波和尾波[16, 36, 52]。对于反射地震成像来讲,一次散射(反射)是信号、是有用信息,需要提取或加强;多次反射和绕射是噪声、是干扰,需要压制或消除。近年来,出现了许多将多次反射视为信号的研究报道。这些报道引起了关于在反射地震偏移成像中多次波到底是信号还是干扰、到底是应该利用还是应该消除的争论。支持者认为,多次波是信号,应该加以利用[56-57];反对者认为,只有一次反射才对偏移有贡献,而多次反射只是干扰,应该加以压制和消除[58-59]。无论是消除还是利用,多次反射问题似乎已经成为了反射地震资料处理中的一个永恒的主题既是一个综合的研究主题,也是一个永恒的争论主题。这也意味着,在反射地震勘探中,多次波问题是一个永远都在路上的前沿和热点问题。
根据散射体的尺度可以将散射过程分为宏观散射过程和微观散射过程两种,简称为宏观散射和微观散射。对于宏观散射,其散射体的尺度与宏观物理现象的尺度相同,一般以米来衡量;对于微观散射,其尺度与微观物理现象的尺度相同,一般以原子或分子的线度来衡量。
在地球物理中,地质体和所考虑的波长均具有宏观尺度;因此,地球物理中的散射是宏观散射。
根据散射波的频率可以将散射过程粗略地分为两类:一类是散射过程对波的频率不产生任何影响,即散射波的频率和入射波的频率相同;另一类是散射波的频率相对于入射波的频率发生了变化,形成了具有一定带宽的离散频谱。形成这种频率变化的原因在于下列经量子力学所证明的事实:分子的极化率以分子的固有振动频率作周期性变化。当入射波的频率与背景介质的分子固有振动频率不同时,两种振动之间产生叠加,形成一个新的振动。该振动的频率与原有的两个频率有关,但是并不相同[60]。
在宏观散射中,由于单个分子或原子所起的作用微不足道,而散射体与入射波的相互作用总体上表现出一种体积效应;因此,在宏观散射过程中一般不会引起散射波和入射波在频率上的不同。换句话说,在地球物理中,一般认为散射波具有入射波的频率和频带,除非散射体是由吸收介质组成的,例如导电岩石或具有黏弹性特点的岩石等等[61]。另外,对于反射地震和瞬变电磁等利用瞬态场的方法,散射发生在入射波所占有的整个频带内,因此很难判断散射过程是否会激发出频带以外的波动。即使会有这种现象出现,也难以将其与非弹性吸收等效应所引起的波形变化区分开来。
与此相反,在微观散射中,单个分子或单个原子在散射过程中起独立或主导作用;从而,在微观散射过程中会出现散射波与入射波在频率上的差异。在物理中,出现这种频率变化的散射过程以拉曼散射和布里渊散射为代表[60]。
在实质上,高频散射理论所研究的是位于均匀或不均匀背景介质中的规则或不规则形体对位于背景介质中的规则和不规则场源所辐射出的电磁波、声波和弹性波场的高频响应。这里,规则形体指的是其表面可以与某个正交坐标系的坐标面重合的散射体;反之称其为不规则形体[2]。类似地,规则场源指的是其辐射场的波前面可以与某个正交坐标系的坐标面重合的场源;反之称之为不规则场源[2]。
在地球内部,三维地质体的形状一般都是不规则的。这意味着,在地球物理问题中三维规则形体非常少见的。尽管如此,规则形体的散射或绕射问题的严格解却是非常重要和非常珍贵的。之所以这样说是因为下列原因:1)利用严格解可以在理论上对散射和绕射等物理现象做出深刻的解释;2)严格解可以作为近似方法和数值方法的检验标准,以考察其可靠性、稳定性和计算精度;3)严格解可以作为研究复杂散射和绕射问题的基础,例如作为GTD和PTD的典则解等等。
在数学上,散射问题属于典型的数学物理边值问题[1-5]。对于位于均匀介质中的规则形体对规则场源和偶极场源的响应,可以通过分离变量法(波函数展开法)得到严格的分析解。然而,除了上文中提到的数量很少和很重要之外,这些解在应用时也不方便。这是因为他们一般是以级数或积分的形式给出的。为了得到数值结果,还需要做大量的复杂计算,尤其是在这些解中含有特殊函数时更是如此。另外,在高频或短波长条件下,像有限差分、有限元等基于网格的数值分析方法以及积分方程或边界元等不基于网格的数值分析方法会遇到难以克服的困难。这是因为在高频或短波长条件下,为了得到满意的精度,计算网格必须要非常地密。这将导致大型或超大型代数方程组的求解问题,以及要面对带有强烈振荡因子的数值积分问题。虽然已经经过了多年的研究,对于这两个问题的解决程度仍然不尽人意。因此,各种解析近似方法应运而生,而高频渐近分析方法就是众多解析近似方法中的一种。
在宏观散射理论中,高频近似等价于远区近似[25]。这是因为,高频渐近分析中的大参数是频率(波数)和距离的乘积[62]。因此,高频近似的精度不仅仅取决于频率是否足够高,而且还取决于距离是否足够大。具体地讲,是取决于频率和距离的乘积是否足够大。因此,虽然与光波和高频电磁波相比,地震波的频率很低(人工地震波的频率一般在200 Hz以下,天然地震波的频率会更低,与光波和无线电波相比是真正的低频波);但是,由于是在远区观测数据,所以依然可以利用高频渐近理论来实现正、反演研究。至于探地雷达中的电磁散射等问题,由于所采用的工作频率很高;所以虽然距离很近,但是依然满足远区条件,可以利用高频渐近散射理论来解决相应的理论和应用问题。
在历史上,对散射的研究起源于光学[1]。从而,关于散射的一些概念也起源于光学。在光学中,散射指的是光在不均匀介质中传播时偏离了入射波的方向而向其他各个方向射去的现象。如果散射体埋置于均匀介质中,则散射波的传播依然满足直线传播定律,只不过其传播方向与入射波的传播方向不同而已。这一点构成了散射与绕射(diffraction,又译为衍射)的根本差别。根据Sommerfeld的定义,任何偏离直线传播定律的现象均称为绕射,而所形成的波称为绕射波(diffracted wave)[1]。根据这个定义,绕射现象可以在入射波遇到障碍体时发生,也可以在没有障碍体的均匀或不均匀介质中发生。实验发现,对于前者,绕射现象只有在障碍体线度与入射波波长基本相当时才出现;而对于后者(主要针对局部波(localized wave)或波束(beam)),指的是局部波或波束在传播过程中,其在垂直于传播方向上的宽度逐渐变大的现象。显然,出现这种现象的原因是波在传播过程中的自然扩散。在理论上,这种扩散现象可以借助于绕射理论(方程)来解释。正是由于这一事实,才把上述自然扩散现象也称为绕射。
与在散射理论中的情形类似,在绕射理论中将障碍体称为绕射体(diffractor)。根据绕射体的几何形状,可以将绕射分为孔径绕射、边缘绕射和表面绕射。其中,孔径绕射和边缘绕射在实质上是一样的,因为在这两种绕射中引起绕射现象的原因都是由于边缘的存在。换句话说,在这两种绕射现象中,绕射波的源都在边缘上。对于表面绕射,主要发生在有限形体(绕射体)上。这时,形成绕射现象的一个基本条件是入射波的传播方向与绕射体表面相切。对于像有限板或有限屏这类只有二维尺度的绕射体,边缘绕射和表面绕射可以同时存在[8, 19, 63]。
虽然边缘绕射和表面绕射看起来完全不同,但是两者在一定条件下是有联系的。严格的数学分析已经证明,边缘绕射在实质上是一种发生在非封闭(开放)表面上的绕射现象[19, 63]。换句话说,边缘绕射是在表面(曲面)上有边缘时而发生的绕射。从这个意义上,可以将绕射笼统地理解为是一种表面效应。与此相反,散射实质上是一种体积效应[23]。
在地球物理中,绕射一般由地层面的不连续点和曲率不连续点,即包括断层、歼灭和不规则界面(例如起伏海底)等一系列具有断点和曲率不连续点的构造所引起。这是目前利用绕射波进行反射地震成像的一个根本原因。
1.2 基本公式本节回顾高频散射理论中的基本方程和基本公式,为下一步的讨论提供基础。为了简便起见,只考虑各向同性介质中标量波和电磁波的结果,而不涉及弹性波以及各向异性条件下的有关结果。关于这些公式的具体来源,参见文献[1-12, 16, 23, 25, 30, 33]等。
1.2.1 波动方程及其弱散射近似令r=(x, y, z)表示空间中任一点的坐标,rs=(xs, ys, zs)代表源点坐标,t代表时间,v(r)代表标量波的传播速度,ws(rs, t)代表场源函数,U(r, t)代表标量波场。若v(r)是光滑函数且U(r, t)具有连续的2阶导数,则
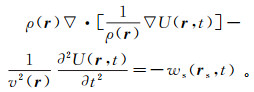 (1a)
(1a) 式中:ρ(r)为密度;∇2=∂2/∂x2+∂2/∂y2+∂2/∂z2。当ρ(r)是常数时,有
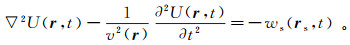 (1b)
(1b) 方程(1)是一个关于标量波场U(r, t)的二阶变系数偏微分方程,称为泛定方程或控制方程(governing equation)。若U(r, t)定义在整个空间,且ws(rs, t)≠0,则方程(1)描述的是全空间中的辐射问题或有源问题;若ws(rs, t)≡0,则方程(1)描述的是全空间中的传播问题或无源问题;若ws(rs, t)=-δ(r-rs)δ(t),则方程(1)描述的是全空间中的点脉冲源辐射问题,此时,U(r, t)称为Green函数,记为G(rs, r; t),即
 (2)
(2) 式中,δ(y)表示关于y的Dirac delta函数。具体地讲,δ(r-rs)表示位于点rs处的点源;δ(t)表示场源信号是在0时刻激发的δ脉冲。如果场源是在非0时刻ts(ts>0)激发的δ脉冲,则应将(2)中的δ(t)替换为δ(t-ts)。
在一般条件下,可以将G(rs, r; t)写成G(r-rs; t-ts)的形式。在均匀介质中,G(rs, r; t)=G(r-rs; t-ts)=δ(t-ts-|r-rs|/v)/(4π|r-rs|)[3]。
在无界区域内,为了保证U(r, t)有物理意义,必须使其满足Sommerfeld辐射条件,即
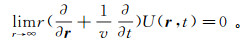 (3)
(3) 式中,r=|r-rs|。
如果所讨论的波动现象被限定在有限空间或者是由分块光滑速度函数所组成的全空间,则除了辐射条件外,在有限空间的边界或速度分函数的间断面上,U(r, t)和G(rs, r; t)还必须满足边界(外边界或内边界)条件[1-3, 7, 16, 25]。
令p(r)=1/v(r)代表慢度。将p(r)拆分为背景慢度p0(r)和扰动慢度pper(r)之和,则有U(r, t)=U0(r, t)+Us(r, t),G(rs, r; t)=G0(rs, r; t)+Gs(rs, r; t)。在这些公式中,下标0代表背景,下标per代表扰动,即U0(r, t)和G0(rs, r; t)分别代表U(r, t)和G(rs, r; t)的背景部分,Us(r, t)和Gs(rs, r; t)分别代表U(r, t)和G(rs, r; t)的散射部分。如果扰动很小,即|pper(r)|/|p0(r)|≪1,则称相应的散射为弱散射;此时,|Us(r)|/|U0(r)|≪1, |Gs(rs, r; t)|/|G0(rs, r; t)|≪1。
令Op(r)=p2(r)-p02(r)=p0pper(r)+pper2(r),则在经过介质和波场拆分后,方程(1b)具有下列形式:
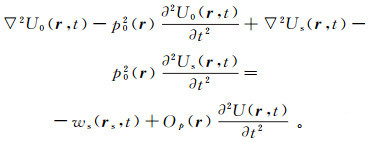 (4)
(4)  (5)
(5) 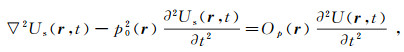 (6)
(6) 则可以将求U(r, t)的问题转化为求U0(r, t)和Us(r, t)的问题。为了解决这个问题,方程(5)所对应的最好是一个简单的数学物理问题。换句话说,U0(r, t)最好是已知的或者是容易算出的;最好是有U0(r, t)的严格精确解;如果没有,也应有U0(r, t)的解析近似解或数值近似解。
一旦求出了U0(r, t),就可以利用(6)求出Us(r, t)。这是一个具有未知场源的复杂辐射问题,只能利用解析近似法或数值近似法求解。然而,在弱散射条件下,方程(6)却可以用积分近似的方式求解(见下文)。事实上,如果在方程(6)的右端舍去Us(r, t), 则得到
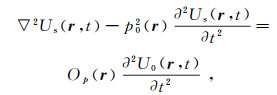 (7)
(7) 假设U0(r, t)为已知;则可以利用第二Green定理求出Us(r, t)的近似积分解(见下文)。
方程(5)和方程(7)是U(r, t)在给定介质拆分方案以及弱散射条件下的泛定方程,称为对方程(1)的弱散射近似。由弱散射近似方程所得到的U(r, t)称为总场的弱散射近似,相应的散射理论称为弱散射理论。
类似地,可以建立Green函数G(r, rs; t)的弱散射近似所满足的泛定方程,其形式与方程(5)和方程(7)完全一样,只不过是要分别把U0(r, t)和Us(r, t)替换为G0(rs, r; t)和Gs(rs, r; t),以及令ws(rs, t)=-δ(r-rs)δ(t)而已。
令ω和i分别代表角频率和虚数单位,则定义Fourier变换对为
 (8)
(8) 和
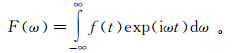 (9)
(9) 式中,f(t)和F(ω)分别为时间域和频率域中的可积函数。
利用上述定义,可以将方程(1)转换到频率域,得到Helmholz方程(常密度)及其弱散射近似:
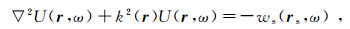 (10)
(10) 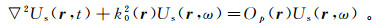 (11)
(11) 式中:O(r)=Op(r)ω2=k2(r)-k02(r);k2(r)=ω2/v2(r), k02(r)=ω2/v02(r), k2(r)和k02(r)是波数。
类似地,可以得到Green函数G(rs, r; t)在频率域中的对偶函数G(rs, r; ω)所满足的方程。在均匀介质中,G(rs, r; ω)=exp[iωτ(rs, r)]/4π|r-rs|。式中,τ(rs, r)是在rs和r之间的传播时间,即τ(rs, r)=|r-rs|/v。
在频率域中,Sommerfeld辐射条件(3)变为
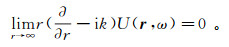 (12)
(12) 对于电磁波,有下式[25]成立:
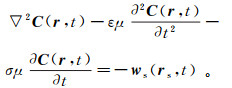 (13)
(13) 式中:ε、μ和σ分别是介电常数、磁导率和电导率;矢量函数C(r, t)代表电场强度矢量E(r, t)、电感应通量矢量(电位移矢量)D(r, t)、磁场强度矢量H(r, t)和磁通量密度矢量B(r, t)当中的任意一个;ws(rs, t)代表矢量场源;∇2算子的定义为∇2C(r, t)=∇∇·C(r, t)-∇×∇×C(r, t)。
对于矢量场,相应的Green函数具有并矢或2阶对称张量的性质,称为并矢Green函数,用G(rs, r, t)表示。与标量Green函数类似,并矢Green函数(rs, r, t)满足下列矢量波动方程:
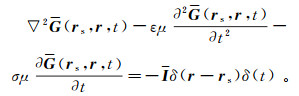 (14)
(14) 式中,I是单位并矢。
在无界区域中,C(r, t)应满足Sillver-Müller辐射条件:
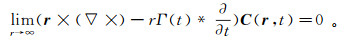 (15)
(15) 式中:Γ(t)是因子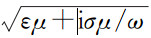
在频率域中,有
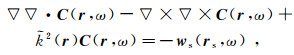 (16)
(16) 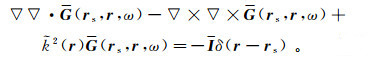 (17)
(17) 其中,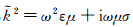
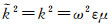
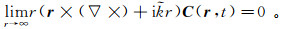 (18)
(18) 现在对



 (19)
(19) 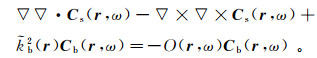 (20)
(20) 类似地,有
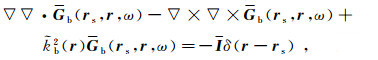 (21)
(21)  (22)
(22) 对于弹性波,上述关于介质和场的拆分方法完全相同,所得到的弱散射近似方程也有类似的形式。考虑到篇幅的限制,建议读者参考文献[16]。
1.2.2 Luneburg-Kline展开与Sommerfeld-Runge试探解上节中所出现的方程均为变系数偏微分方程,其经典解法主要有两种,即级数或渐近级数法和积分方程法。Luneburg-Kline展开与Sommerfeld-Runge试探解(Sommerfel-Runge ansatz)属于渐近级数法。
对于标量波,在k→∞时,有
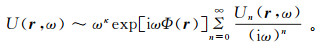 (23)
(23) 式中:因子ωκ(-1 < κ≤0)是专为描述绕射波而引入的,对于直达波、反射波和透射波等非绕射波,κ≡0;相位函数Φ(r)称为程函(eikonal),满足程函方程(eikonakl equation)|∇Φ(r)|2=p2(r);因子Un(r, ω)是振幅函数,满足输运方程2∇Un(r)·∇Φ(r)+Un(r)∇2Φ(r)=-∇2Un-1(r),其中,U-1(r)≡0。
对于电磁波,假设μ=μ0(真空或空气中的磁导率),有
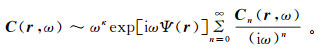 (24)
(24) 式中,|∇Ψ(r)|2=εμ0,2[∇Ψ·∇]Cn(r)+[∇2Ψ(r)]Cn(r)=-∇2Cn-1(r),Cn-1(r)=0。
对于弹性波,将式(24)中的电磁矢量C(r, ω)和Cn(r, ω)换为位移矢量u(r, ω)和un(r)即可。
在现代地球物理文献中,Luneburg-Kline展开又称为几何射线级数或射线级数,其首项(n=0)即为Sommerfeld-Runge试探解。在现代文献中,将这个试探解称为几何光学近似、几何光学场或零阶射线近似(zero-order ray approximation)。基于零阶射线近似的波动理论称为零阶射线理论(zero-order ray theory)。对于地震波,方程(23)中的相位函数即为沿射线的传播时间(ray traveltime),称为射线走时,记为τ(r)。因此,几何光学场(Ugo(r, ω))或零阶几何射线场(UART(r, ω))的形式为
 (25)
(25) 式中:A(r)代表UART(r, ω)的振幅;τ(r)代表走时。如果ws(rs, ω)=1,则Ugo(r, ω)转化为Green函数的几何光学近似Ugo(rs, r; ω)。在非吸收介质中,A(r)和τ(r)均与ω无关。
在文献中,几何光学近似亦称为WKB近似或WKBJ近似[8]。
1.2.3 表示定理及其近似表示定理是相应波动方程的直接积分[16, 25]。对于标量波,在只有一个散射体时,对方程(1a)和方程(2)先施以Fourier变换,再利用第二Green定理得到
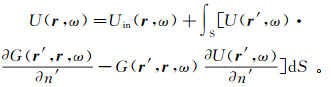 (26)
(26) 式中:S是包围所研究区域的光滑封闭曲面;n′代表S的外法线方向;r′是S上任意一点(Green函数的源点)的坐标矢量;Uin(r, ω)是入射场,由场源直接产生,其表达式为
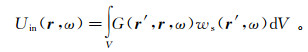 (27)
(27) 式中:V代表被S所包围的体积;r′代表V中的点。
如果有多个散射体存在,则在方程(26)的右端应该有多个面积分。
表示定理(26)所给出的是方程(1)的形式积分解,因为总场还出现在积分号内。为了得到近似积分解,利用Kirchhoff近似边界条件,得到Kirchhoff近似:
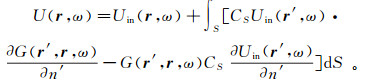 (28)
(28) 式中,CS代表平面波反射系数和透射系数。由于Kirchhoff近似只考虑S的亮区,所以在方程(28)中的S已经不再是封闭曲面。
类似地,对于电磁场C,在单体散射条件下,有
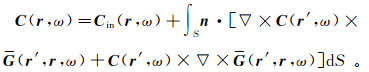 (29)
(29) 如果有N个散射体存在,则在方程(29)的右端应该有N个面积分。
对于C(r′, ω),同样可以利用Kirchhoff近似边界条件。此时,应将平面波反射和透射系数替换为相应的反射和透射系数张量(矩阵)。
上面给出的表示定理中均含有面积分,在本文中称为基于面积分的表示定理。如果速度是光滑函数且在磁导率是常数的假设下,可以得到下列基于体积分的表示定理:
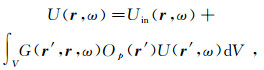 (30)
(30) 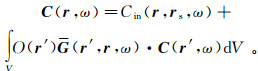 (31)
(31) 在弱散射近似下,方程(30)、(31)变为相应的Born近似,即
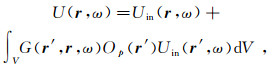 (32)
(32) 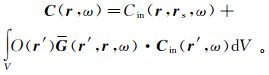 (33)
(33) 不难看出,Born近似和Kirchhoff近似有一个共同点,即都是对总场实施近似。其中,Kirchhoff近似是在散射(反射或透射)面上用局部平面波的反射或透射场来近似总场,而Born近似是用背景场(入射场)来近似散射体内的总场。与这两种方法不同,Rytov近似是将求总场的问题转化成为求相位的问题。为此,Rytov假设U(r, ω)=exp[iψ(r)]。将这个试探解带入方程(10),得到i∇2ψ(r)-|∇ψ(r)|2+k2(r)=0。这是一个关于ψ(r)的非线性方程。为了解这个方程,令ψ(r)~ψ0(r)+ψ1(r),并假设ψ(r)很小,即有|ψ1(r)|2~0。由此得到
 (34)
(34) 式中,U0(r, ω)=exp[iψ0(r)]。对方程(34)应用第二Green定理,得到
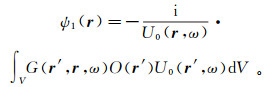 (35)
(35) 从而,U(r, ω)≈URytov(r, ω)=U0(r, ω)·exp[iψ1(r)]。式中,下标Rytov表示Rytov近似。
对于矢量波,在原则上应该可以得到类似的近似。然而到目前为止,笔者还没有见到与此有关的任何报道。
1.2.4 Kirchhoff、Born和Rytov之间的关系在方程(35)的两端同乘上-iU0(r, ω),得到UBorn(r, ω)=iU0(r, ω)ψ1(r)。式中,下标Born表示Born近似。当|ψ1(r)| < 1时,有exp[iψ1(r)]≈1+iψ1(r), 即iψ1(r)U0(r, ω)≈URytov(r)-U0(r)。从而,URytov(r, ω)≈U0(r, ω)+UBorn(r, ω)。这是Born近似和Rytov近似之间的关系[23]。为了建立Kirchhoff近似和Born近似之间的关系,首先需要将扰动限定在反射面之下[64]。因此,这种关系只对反射波成立。在数学上,可以通过引入Heaviside阶跃函数来描述上述扰动,即OH(r)=[p2(r)-p02(r)]H[ΣR(r)]。式中:ΣR(r)是描述反射面的隐式方程,即ΣR(r)=0;H(r)是Heaviside函数。在反射面之上,H(r)=0;在反射面之下,H(r)=1。假设反射面为无界曲面且有连续的法线。
首先,在方程(28)和(32)中用几何光学场来近似Green函数,并舍去关于振幅的导数,得到
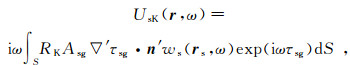 (36)
(36)  (37)
(37) 式中:Asg(r′)=AsP(r′)AgP(r′);τsg(r′)=τsP(r′)+τgP(r′);n′是单位外法线矢量;下标K表示Kirchhoff近似;下标B表示Born近似;下标sK表示在Kirchhoff近似下的散射场;下标sB表示在Born近似下的散射场;RK=Rc,Rc是平面波反射系数;下标sg表示由源点到接收点;下标s表示源点;下标g表示接收点;下标P代表界面S上(体积V内)的流动点;∇′表示对r′求梯度。为了简便起见,在积分号内略去了变量r′。
其次,利用关系式dV=dΣIdnI=dΣIdτ/|∇r′τ|和RB=α(r)/4cos2θP(RB为Born反射系数;α(r)=v0(r)/v(r)-1;v0(r)为背景速度;v(r)为介质速度;θP=(1/2)arccos(∇r′τsP·∇r′τgP/|∇r′τsP·∇r′τgP|)),可将式(37)中的体积分转化为等时面叠加[64],即
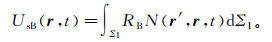 (38)
(38) 式中:下标I表示与等时面有关的量;ΣI代表等时面;nI是垂直于等时面的距离;N(r′, r, t)是与振幅Asg(r′)及走时τ(r′)有关的函数。
类似地,可以将Kirchhoff积分式(36)转换为等时面叠加,得到
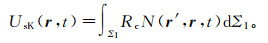 (39)
(39) 对比式(38)和式(39)不难看出,UsB(r, t)和UsK(r, t)之间的差别仅在于反射系数RB和Rc的不同[64]。
1.2.5 广义Born近似令GRay(rs, r, ω)=Ggo(rs, r, ω)=A(r)·exp[iωτ(r)]表示Green函数的几何光学(零阶射线)近似,将其带入到方程(10)并令ws(rs, ω)=δ(r-rs),得到
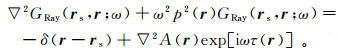 (40)
(40) 这是一个关于GRay(rs, r, ω)的精确方程。其中,∇2A(r)exp[iωτ(r)]相当于一个误差项。
对方程(40)应用第二Green定理,得到
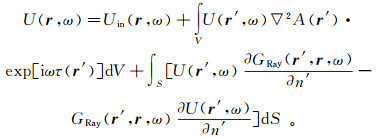 (41)
(41) 如果V占据整个空间,则式(41)右端的面积分为0。从而,
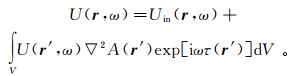 (42)
(42) 式(42)是关于U(r, ω)的形式积分解。若将r置于散射体内,得到一个关于U(r, ω)的积分方程,其解可以表示成为Neumann级数。这个级数的前两项之和为
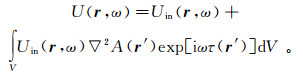 (43)
(43) 进一步,用URay(r, ω)近似Uin(r, ω),得到
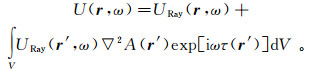 (44a)
(44a) 式(44a)即是Coates和Champman[13]在1991年提出的声波广义Born近似。对于弹性波有类似的公式,具体见文献[13]。
如果密度不是常数,则利用式(1a)和式(40)得到下式[13]:
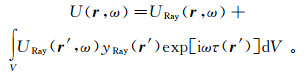 (44b)
(44b) 式中:下标Ray表示射线近似;yRay(r′)=[∇2A(r′)-∇A(r′)·∇ρ(r′)]/ρ(r′)。
1.2.6 高频渐近Green函数高频渐近Green函数包括几何光学(零阶射线)近似、高斯波束叠加近似、delta波包叠加近似、Kirchhoff型积分近似、Born型近似以及Rytov型近似。其中:几何光学近似又称为Sommerfeld-Runge试探解;高斯波束叠加近似是一个积分,其被积函数是高斯波束;delat波包叠加近似是高斯波束叠加近似在时间-空间域中的对偶形式;Kirchhoff型积分近似、Born型近似以及Rytov型近似是在公式(28)、(29)、(32)、(33)、(35)及(44)中令震源函数ws(rs, ω)恒等于1。鉴于这一事实,在下文中只给出几何光学(零阶射线)近似、高斯波束叠加近似以及delta波包叠加近似的表达式。
1)几何光学近似(零阶几何射线近似)
高频渐近Green函数的最简单表示是下列几何光学(零阶几何射线)近似:
 (45)
(45) 式中:A(rs, r)代表UART(rs, r, ω)的振幅;τ(rs, r)是在rs和r之间的射线走时。在非吸收介质中,振幅A(rs, r)和走时τ(rs, r)均与ω无关;在均匀介质中,通过与精确公式G(rs, r; ω)=exp[iωτ(r)]/(4π|r-rs|)对比,得到A(rs, r)=1/(4π|r-rs|);在非均匀介质中,A(rs, r)只能通过数值方法求得[10]。同样的结论也适用于τ(rs, r)。
2)高斯波束叠加近似
令s和q=(q1, q2)分别表示中心射线上流动点M到参考点M0(s0)之间的弧长和在M点垂直于中心射线的坐标,θ和φ分别表示球坐标中的极角和方位角,则加了滤波因子之后的高斯波束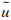
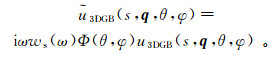 (46)
(46) 式中:ws(ω)表示震源子波的频谱;Φ(θ, φ)=ΦR(θ, φ)+isgn(ω)ΦI(θ, φ)是加权函数;u3DGB(s, q, θ, φ)=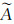
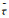
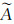
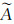
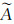
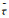
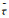
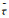
对于2维情况,公式(46)变为
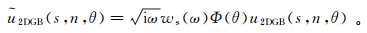 (47)
(47) 式中:u2DGB(s, n, θ)=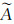
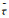
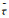
利用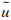
 (48a)
(48a) 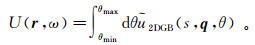 (48b)
(48b) 式中,θmin和θmax、φmin和φmax给出高斯波束叠加的范围。
令ws(ω)=1,则公式(46)和(47)转变为Green函数G(rs, rg, ω),即
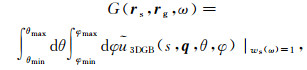 (49a)
(49a) 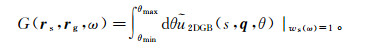 (49b)
(49b) 在文献中,一般取θmin=0、θmax=π、φmin=0和φmax=2π。另外,利用sinθdθdφ~dpxdpy/pz(二维情形为dθ~dpx/pz)可以将对角度的积分(在单位球面上的面积分)转化为对慢度的积分,积分区域为由px和py所构成的无界平面。虽然这种对慢度的积分形式在地球物理文献中广为出现,但是在实际上必须对无界积分进行截断。因此,与文献中在慢度空间中所给出的叠加公式相比,公式(48)和(49)更接近于实际计算。
3)delta波包叠加近似
在时间域中,利用Fourier反变换公式(9)将公式(49)变为下列形式
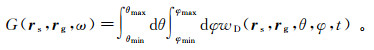 (50)
(50) 式中,
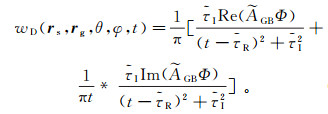 (51)
(51) 式中,*表示褶积。
根据Červený在1982年所给出的定义,wD(rs, rg, θ, φ, t)称为delta波包。值得注意的是,函数
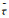
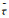
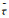
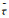
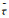
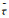
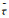
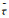
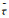
本节的目的是对若干已经在上文中提到的物理概念和数学内涵进行评述和强调。进行这种评述和强调的目的是期望澄清一些与散射理论不相容的说法和论断。这些说法和论断不仅出现在中文文献中,也出现在英文文献中。
首先,散射波由位于入射波传播路径上的障碍体所引起。没有障碍就没有散射。在物理上,障碍体的表面是介质参数的间断(不连续)面。因此,间断是产生散射波的充分必要条件,没有间断就没有散射。然而,间断是有阶次的[10]。在文献中,一般将介质参数的间断称为1阶间断;将介质参数1阶导数的间断称为2阶间断;将2阶及大于2阶导数的间断称为高阶间断。一般来讲,N阶间断面指的是物理参数的N-1阶导数的间断面。无论是1阶间断、2阶间断还是高阶间断,都可以引起散射,只不过是散射强度的不同而已。因此,对于非均匀散射体而言,散射是一种体积效应;而对于均匀散射体来讲,散射是一种面积效应。从这个意义上讲,如果散射体内没有2阶或高于2阶的间断存在,散射波应该用面积分描述。反之,如果散射体内有2阶或高阶间断存在,则应该用体积分来计算散射波。
其次,散射问题所导致的数学物理问题是偏微分方程的边值问题[2-3, 7-9, 65]。因此,散射波的产生和传播分别受边界条件、泛定方程和辐射条件所制约。具体地讲:边界条件决定是否有散射波产生、有什么样的散射波产生以及有多强的散射波产生;波动方程决定散射波在传播过程中的特点与性态,即沿着什么样的路径传播,是以相速度传播还是以群速度传播,从场源点到接收点之间的传播时间是多少,在传播过程中振幅和相位是如何变化的,等等;辐射条件限定散射波在无限远处应该有的性态,即必须有与函数eiωτ(rS, r)/|r-rs|相同的衰减规律[2-3, 7-9]。
除了上述条件之外,散射波的产生与否和分布规律还与障碍体的几何形态及空间尺度(线度)有关。其中,几何形态决定散射波的空间分布,空间尺度决定是否有散射波产生和有什么样的散射波产生。具体地讲,在远离散射体的观测区域内,散射波的空间分布可以用函数f(θ, φ)eiωτ(rs, r)/|rs-r|来统一描述[2]。其中,θ是极角;φ是方位角;因子f(θ, φ)是描述散射波空间分布的函数,直接与障碍体的几何形状有关[1-2, 9]。如果障碍体的尺度远远地大于波长,则二次波以反向散射为主,形成反射或漫反射;此时,f(θ, φ)的非零值具有优势分布方向,满足反射定律。反之,如果障碍体的尺度远远地小于波长,则障碍体的存在对入射波基本没有影响,所形成的二次波以前向散射为主;此时,f(θ, φ)的优势分布方向与入射波的传播方向基本一致。如果障碍体的尺度接近或等于波长,则所形成的二次波将绕着障碍体传播,形成绕射波[1, 9, 12];此时,f(θ, φ)的优势分布方向受绕射定律控制。只有在障碍体的线度远大于波长,但是还没有达到远远地大于波长的程度,f(θ, φ)的非零值才会没有优势分布方向,形成散射波[1, 9]。
虽然上述讨论主要针对散射波,但所得出的结论却具有普遍意义。事实上,反射、透射、绕射和散射等均是二次波(secondary wave),均来自于入射波和障碍体之间的相互作用[1, 3, 9, 23, 25]。从而,他们的出生条件和出生后的性态完全取决于边界条件和入射波在边界上的性态,与偏微分方程(波动方程)本身无关。因此,有边界存在是产生二次波的首要条件,没有边界就没有二次波。一旦具备了这个首要条件,下一个对二次波出生有重要影响的条件就是边界两侧的介质参数反差。这个反差越大,二次波就越强。反之,二次波就越弱。如果边界两侧的介质参数只有微弱的反差,则只能导致微弱的二次波。如果二次波微弱到难以观测的程度,则在实际上跟没有边界存在的效果是一样的。在边界的存在性和介质性质反差的强弱性都达到要求以后,对二次波起决定性影响的就是障碍体的线度和其几何形态。如果障碍体的线度远远地大于入射波的波长,则波与边界的作用满足局部化原理。这时,二次波的初始强度和初始传播方向均由实验定律所决定;具体地讲,是由反射和折射定律以及绕射定律所决定。反之,则局部化原理不成立。此时,二次波的强度只能根据Kirchhoff-Huygens原理来计算,而其传播方向在原则上可以是任意方向[9, 23, 25]。
当上述所有条件均满足二次波的出生条件后,二次波的出生阶段即宣告结束,到了成长和消亡阶段,即传播阶段。一旦到了这个阶段,边界就不再起任何作用。事实上,在传播阶段,只有波动方程才能对散射波进行控制和管理[1, 3, 9, 23, 25]。
从数学物理的角度来看,不存在专门描述入射波、反射波、透射波、绕射波和散射波的偏微分(波动)方程[65]。文献中所报道的各种单程波动方程均来自于对常规双程波动方程的近似,是纯数学产物,与物理现实无关。事实上,从弱散射近似方程(32)和(33)的建立过程可以看出,这两个方程中的体积分所描述的并不是真正意义上的散射场,而是一种形式上的散射场。这个场既受介质拆分方案的制约,又受Green函数近似的影响,但是却与物理现实无关。正如Coates和Chapman所指出的那样,不同的介质拆分方案将会导致不同的散射场[13]。这与数学物理中的唯一性原理相悖。关于这一点,已经在引言中有所提及。这里再一次提到这一点,是为了能够引起读者的重视。
最后,尽管波动方程所描述的是全部的波动现象,但是其严格或近似分析解却由单向传播的波函数所组成,所有这些波函数的叠加形成了最终的总场。因此,在探求波动方程的严格或近似分析解的过程中,必须对不同类型的波场分别求解。换句话说,在严格解和解析近似解中,对每一种波都需要一个数学表达式,而全部这些表达式的叠加(求和)即为总场的数学表达式。例如,在高频渐近波动理论中,必须对反射波、透射波及绕射波进行专门的求解。根据上文,这种求解所依据的是在边界上波场所满足的实验定律而不是波动方程;因为波动方程描述不了波与介质的相互作用。换句话说,只有通过边界条件才能模拟出二次波。这从另一个侧面强调了上文中所列举的事实,即波动(偏微分)方程只控制波场传播,而是否有二次波产生和有什么样的二次波产生却要受制于边界条件、边界形状和边界尺度。与此相反,数值解同时包括上述各种波现象且无法分开。因此,尽管数值模拟可以提供比高频渐近理论更为精确的模拟结果,但是对其内涵的认识却离不开高频渐近波动理论的指导。
2 研究历史与研究现状如上所述,高频渐近散射理论来自于下列3个途径:1)对散射问题严格解进行高频渐近分析;2)对典则问题的严格解进行高频近似,通过对比得到相应的系数或函数;3)对波场表示定理的线性和非线性近似。其中,第一个途径只适合于均匀介质、规则场源和规则散射体,而第二和第三个途径不仅适合于第一个途径所能解决的散射问题,也适合于处理任意复杂介质中任意复杂场源和任意复杂散射体所引起的散射问题。考虑到当今地球物理中散射问题的基本特征(复杂介质和复杂形态),以及考虑到在引言中已经对第二种途径的研究历史和研究现状进行过简要的说明和评述这一事实,在下文中将只对第三个途径,即对的波场表示定理的线性和非线性(拟解析)近似研究历史和研究现状进行简要综述。
在数学上,波场表示定理是散射问题的形式积分解[3, 16, 25]。这里,“形式”二字表示下列事实,即在表示定理中未知总场不仅出现在等号左端,而且还作为被积函数出现在等号右端的积分内。因此,对表示定理的近似就是对积分号内的总场来进行近似。如果对总场的近似是利用一个已知函数来实施的,则可将形式积分解转化成为一个积分,得到散射问题的近似积分解;这种近似称为线性近似,因为总场和其近似之间的关系是线性关系。如果对总场的近似是利用一个未知函数来实施的,则形式积分解将转化为一个积分方程;这种近似称为非线性近似,因为总场和其近似之间的关系是非线性关系。
除了对总场的近似外,在从形式积分解到近似积分解的转化过程中还需要对入射场和Green函数进行近似。这主要是因为表示定理来源于对第二Green定理的应用,需要假设入射场和Green函数为已知。如果入射场和Green函数均为相应辐射问题或边值问题的精确解,则所得到的积分将对所有的频率有效,即为全频带近似;如果对入射场和Green函数均采用其高频渐近,则将导致高频渐近散射理论,这是一种只对所研究频带内的高端部分或只对远区成立的近似;类似地,如果对入射场和Green函数均采用其低频渐近,则将导致低频渐近散射理论,这是一种只对所研究频带内的低端部分或只对近区成立的近似,称为似稳场近似或准静态近似;因为对于近区来讲,主要是传导和感应效应而非传播效应(针对电磁场而言)。对于处于高频和低频之间的过渡频率,或者是对于介于远区和近区之间的过渡区内的散射问题,则一般难以通过近似方法给予满意的解决;对于这种情况,一般需要利用数值方法进行研究。
因此,给定近似积分解的适用频带和对介质复杂程度的适应程度完全取决于对Green函数和入射场的近似方式。在本文中,由于仅考虑入射场和Green函数的高频近似,所以不涉及低频和过渡频带内的散射理论。另外,在几何射线及高斯波束叠加理论的框架中,Green函数和入射场均采用几何光学近似或其波束扩展的叠加,因此除了震源函数的形式外,这两者在数学形式上没有差别。所以,在下文中将仅对波场表示定理的近似方式、高频渐近Green函数的导出过程,及其在地球物理中的应用进行概略地回顾与评述。
2.1 波场定理及其线性化如上所述,波场表示定理是波动方程的形式积分解,是标量和矢量Green公式在解决声波和弹性波散射问题中的具体应用[3, 16, 25]。在数学上,形式积分解有两种表现形式,即面积分形式和体积分形式。其中,面积分形式定义在散射体的表面上,而体积分形式定义在散射体所占据的空间上。形成这两种形式的原因在于建立形式积分解时所应用的推导策略不同:在面积分形式积分解的推导过程中,假设波所通过的介质具有分区光滑的特点,从而在每一个分区中分别应用相应的Green公式;而在体积分形式的推导过程中,假设介质和场均为背景和扰动两部分之叠加,而将扰动部分作为二次场源来处理,从而不考虑扰动在边界上不连续性的影响。
无论是面积分形式还是体积分形式,均具有很强的非线性,这是未知的总场出现在积分号内所形成的结果。基于同样的原因,形式积分解不能直接用于解决实际问题。为了克服这个困难,文献中提出了2种途径:1)通过直接或间接归化将相应的形式积分解转化成为积分方程,利用数值方法解决散射场的计算问题;2)对总场进行近似,将形式积分解转化成为近似积分解。由于第一种途径主要用于解决数值模拟问题,所以在本文中不考虑与这一途径有关的问题。对于第二种途径,又分为线性化近似和拟线性化近似2种。目前为止,线性化近似已经分别被用于近似表示定理中的面积分和体积分,而拟线性近似的基本思想只在近似体积分的过程中得到了应用。换句话说,到目前为止,还没有关于对面积分采用拟线性近似的报道。
在上文所提到的线性化近似中,对面积分和体积分采用了不同的方法。假设入射波在局部为平面波(高频或远场近似)而散射面在局部接近于平面(切平面近似),则可以将散射面上的总场近似地表示成为平面波反射系数与入射场的乘积。此类近似称为Kirchhoff近似。而由此类近似所导致的面积分称为Kirchhoff积分或Kirchhoff-Holmholtz积分,又称为Kirchhoff-Holmholtz积分定理(也称为Helmholtz-Kirchhoff积分定理)[1, 9, 16, 23, 58]。由于在其建立过程中对散射面两侧的介质反差强度没有做任何假设,所以Kirchhoff近似是一种可以适用于任何散射强度的近似。
与对面积分的线性化近似只有Kirchhoff近似一种不同,对体积分表示的线性化近似有两种。对于第一种近似,如在上文中已经提到的,需要将介质拆分为背景与扰动两部分,而扰动部分充当散射体的角色。进一步,在第一种近似中,假设在散射体内的散射场远远小于入射场,从而可以在积分号内忽略散射场的贡献,用入射场近似代替总场。由此类近似而产生的体积分表示称为Born近似。由于只有在介质扰动比较小时才可以在散射体内忽略散射场对二次场源的贡献,所以文献中将Born近似理论称为弱散射理论。若将Born近似作为相应积分方程迭代解的初始项,则可以构造出相应散射问题的Born级数近似解。因此,又将常规的Born近似称为1阶Born近似[9, 23]。对于第二种近似,其基本思想是事先假设总场所具有的数学形式,然后再进行近似。具体地讲,在第二种近似中,首先要假设总场在传播的同时还具有衰减的特点,从而可以用一个具有单位振幅的复指数函数来表示。这样一来,就将对场的求解问题转化成为了对复相位的求解问题。在历史上,这个转化由前苏联物理学家Rytov研究无线电波在随机不均匀电离层中传播时所提出,因此被称为Rytov近似。与Born近似一样,在建立Rytov近似时需要对介质进行拆分并要求扰动为小量;因此,Rytov近似也是一种弱散射近似。然而,与Born近似不同,在Rytov近似中所研究的是扰动对复相位的影响,而不是对场本身的影响。
现在讨论对体积分表示定理的拟解析近似。在数学上,拟解析近似的出发方程与Born近似的出发方程完全一样,唯一不同的是假设散射场在散射体内与入射场成正比而不是0,其比例函数称之为反射函数[26-27]。为了求出反射函数,在拟解析近似中利用了Green函数的奇异性:假设在Green函数奇点处的反射函数值对所考虑的体积分的贡献最大,而其他点上的反射函数值对体积分的贡献可以忽略。因此,可以将反射函数提到所考虑的体积分之外,并由此而得到一个关于反射函数的近似表达式。利用这个表达式,即可以得到散射场的近似积分表示[26-27]。
在地球物理中,基于几何光学(零阶几何射线)场的Kirchhoff、Born和Rytov近似均得到了广泛的应用,分别被称为Ray-Kirchhoff、Ray-Born和Ray-Rytov近似。事实上,正如在引言中所提到的,上列近似是众多地震波传播与散射理论研究、数值模拟研究、偏移成像研究、反射与透射地震层析成像研究、全波形反演研究以及地震波干涉成像研究等热点方向的出发方程或数据模型[42-43];然而,由于基于几何射线理论的Green函数和入射场在非正则区(临界区、过渡区和焦散区)内失效[2, 7, 10],且在复杂地下介质中非正则区是广泛存在的,所以Ray-Kirchhoff近似和Ray-Born近似在地球物理中的应用受到了一定的限制。为了克服这个弱点,可以利用高斯波束叠加(Gaussian beam summation)来替换上述基于几何射线理论的Green函数和入射场[10, 66-67]。由于高斯波束(Gaussian beam)是波动方程的一种只在几何射线周围成立的高频渐近解且具有处处正则性[10, 66-67];所以在进行了上述替换后既可扩大Kirchhoff近似、Born近似和Rytov近似的应用范围,又可以保持Ray-Kirchhoff近似、Ray-Born和Ray-Rytov近似所具有的灵活性和计算效率。然而据笔者所知,到目前为止,这种替换只在Kirchhoff近似和Born近似中得到了实施,而未见关于在Rytov近似中用高斯波束叠加表示Green函数的报道。
2.2 几何射线级数理论及其应用几何射线级数理论源于光学,由出生于德国的美籍学者Luneburg[15]在19441948年间提出。在此之前,关于几何光学数学基础的研究当属Sommerfeld和Runge在1911年合作发表的工作。在采纳了Debye的建议(几何光学的基本方程程函方程或许可以在波长趋近于0的条件下从标量波动方程中推导出来)之后,Sommerfeld和Runge假设光波是频率为f的简谐波(harmonic wave),且在短波极限下(波长趋近于0或ω=2πf→∞)具有A(r)eik0ψ(r)的形式[1, 8-9, 15]。式中:k0=ω/c=2π/λ0是真空中的波数;c是真空中的光速;λ0是真空中的波长;ψ是光程;r是空间坐标矢量。利用试探解U(r, ω)=A(r)eik0ψ(r),Sommerfeld和Runge推导出了程函方程并由此而得出结论:几何光学是波动方程在短波长极限下的渐近解[1, 9]。19441948年,Lunebug从不同角度对几何光学的数学基础问题进行了研究。与Sommerfeld和Runge不同,Luneburg的研究是在时间域中展开的。通过对比,Lunebug发现,几何光学理论中的程函方程和Maxwell方程组的特征方程(控制Maxwell方程组不连续解传播过程的方程)在形式上等价。根据这种等价性,Lunebug将几何光学场等同于分布在一个运动着的不连续面上的电磁场。以这种方式,Lunebug证明了几何光学与Maxwell电磁理论之间的关系,即几何光学是Maxwell方程组的一种严格特解。利用这个特解,Lunebug推导出了几何光学中的全部方程和公式。同时,利用其在19471948学年间两次在New York大学讲课的机会,Lunebug花了很多时间论证他本人的工作与短波长极限方法之间的关系。由此而产生的一些想法和结果形成了利用渐近级数解Maxwell方程组的基础,并在此基础上逐渐发展成为了射线级数理论[1, 6, 15]。
1959年,Karal等[20]将几何射线级数的基本思想用于解决弹性波在非均匀介质中的传播问题,为这个方法在地震学中的应用提供了理论基础。与此同时,前苏联的一些理论工作者对于射线级数本身的收敛性、有效范围、高阶项的具体形式及其在非正则区内的表现形式等问题进行了深入的研究。作为这些研究的成果,前苏联的科学家Babich、Brekhovskikh以及Kravtsov等人出版了一系列专著。到了20世纪80年代,这些专著被逐渐翻译成了英文并在西方出版[7, 68-69]。与此同时,西方的一些应用数学工作者也开展了大量的研究工作。在前苏联和西方波动理论工作者的共同努力下,先后建立了专门描述非正则区内波场分布的几何绕射理论、边界层法、抛物方程法、特殊渐近级数法、标准积分叠加法、Maslov法、复射线法和高斯波束叠加法等等一系列理论和方法[7, 10, 68-71]。在这些理论和方法中,除了高斯波束叠加法之外,其他方法都需要先识别出焦散区的位置,然后才能在焦散区内利用相应的积分表达式来替代几何射线理论公式,进而实现对焦散区内波场分布的描述和计算[67, 70];这一点限制了这些方法在地震波偏移和反演成像中的广泛应用。与此相反,高斯波束叠加法不需要识别焦散区的位置,因此可以自动地计算出焦散区内的波场分布[10, 66-67, 71];这是高斯波束叠加法目前在地震波偏移成像中得到广泛应用的一个重要原因。
在前苏联和西方一些波动理论学家和应用数学家致力于建立关于射线级数表达严格数学理论的同时,以Červený为代表的一些捷克地震学家却把工作的重点放在了零级射线理论上(只取几何射线级数首项的理论称为零级几何射线理论)。在他们的努力下,在20世纪80年代,一些起源于前苏联的概念逐渐在西方变得广为人知,例如射线中心基坐标(ray-centered Coordinate system)、傍轴射线近似(paraxial ray approximation)、动力学射线追踪(dynamic ray tracing)和高斯波束(Gaussian beam)等等。在前苏联的工作基础之上,捷克的研究者们系统地建立了基于传播算子(矩阵)的傍轴射线理论(又称为point-to-point propagator theory)、动力学射线追踪理论以及相应的计算技术,并开发了一系列计算程序。同时,为了解决非正则区内射线理论的失效和奇异性问题,Červený所领导的团队将傍轴射线理论和高斯波束的基本思想结合在一起,建立了利用高斯波束及其叠加来模拟地震波场的基本理论和计算技术[10]。
到了20世纪90年代,几何射线理论被广泛地用于建立Kirchhoff型真振幅成像理论和积分类反演理论。其中,Bortfeld将矩阵光学的基本思想引入到勘探地震学中,建立了既简洁又适合于解决反射地震成像问题的傍轴射线矩阵理论,又称为surface-to-surface propagator theory[71-74]。以这个理论为工具,Bortfeld、Hubral和Tygel等[39, 72, 75]系统地研究了与傍轴射线理论、反射地震真振幅成像以及Kirchhoff-Holmholtz积分反算子等有关的一系列理论问题,得到了丰富的成果。同时,Beylkin[31-32]、Bleistein[34-37]及de Hoop等[76]利用Ray-Kirchhoff积分和Ray-Born近似理论建立了系统的高频渐近反演理论。在这些工作中,Beylkin和Bleistein的工作具有划时代的意义:Beykin提出了著名的Beykin行列式并建立了奇性反演理论;而Bleistein奠定了在偏移的过程中进行反演的基础,即多重加权理论,又称为偏移加反演(migration/inversion)理论[35, 37]。
近年来,对高斯波束或基于高斯波束叠加的标量或矢量Green函数的应用受到了众多地震成像与反演理论研究者的重视,出现了一大批研究成果[77-85]。事实上,如今高斯波束法已经成为了处理任意复杂非均匀各向异性介质和各种复杂黏弹性介质中波场传播和成像问题的有力工具[10, 84]。
以上所讨论的结果均是在频率域或频率-空间域(f-x域)中得到的。在时间域或在时间-空间域(t-x域)中,几何射线理论中的相位因子(走时)将变为δ函数,其对震源子波的作用是沿时间轴的简单平移;而振幅因子对震源子波的作用是对其幅值进行几何扩散标定(非吸收介质)或几何扩散标定加滤波(吸收介质)。类似地,在t-x域中高斯波束将转化为delta波包,其对震源子波的作用恒为几何扩散标定加滤波[85]。除了这些以外,时间域中的计算要显得复杂很多,因为在时间域中,所有在频率域中的乘积均转化为褶积。然而,由于Fourier反变换的作用,所有在频率域中出现的振荡积分将转化为非振荡积分,因此避开了振荡积分所带来的问题。从这个意义上讲,频率域表示和时间域表示各有千秋,其应用效果和数值计算的复杂程度随着所要解决问题的变化而变化。换句话说,应该根据所要解决的问题来决定采用频率域表示还是采用时间域表示。
2.3 Kirchhoff积分、Born近似以及Rytov近似如上文所述,Kirchhoff积分起源于光学,其核心内容是两个Kirchhoff近似边界条件。最初,Kirchhoff积分只用于均匀介质中的孔径绕射问题[1, 9]。随着时代的发展,Kirchhoff积分被逐渐用于解决非均匀介质中的标量(声)和矢量(电磁、弹性)波传播和绕射(散射)等问题[7, 25, 86-87]。在这种应用中,精确的标量或张量(并矢)Green函数和入射场被替换成为近似的几何射线(几何光学)Green函数和几何光学场[7, 25, 86-87]。
在地球物理中,Kirchhoff积分主要被用于研究非均匀介质中的地震波传播规律和散射特征以及偏移成像与反演等理论和方法技术问题[33, 52-53]。在经过了几十年的研究之后,在几何射线理论的基础之上,已经建立起了完整的基于Kirchhoff积分或Kirchhoff型积分的地震波数值模拟和反射地震成像理论体系,包括数学表示和数值计算方法,并在石油与天然气等资源勘探中得到了广泛应用[33, 40-41]。此外,在反射地震成像理论研究的推动下,几何射线理论本身的研究已经取得了一系列重要进展,提出了若干关于地震波传播的定理和公式,极大地丰富了地震波高频渐近理论的内涵[37, 52-53, 72-74, 88-89]。
在文献中,基于零阶射线(几何光学)Green函数的Kirchhoff积分有时被称为Ray-Kirchhoff积分。关于这一点,在上文中已经有过提及。由于射线理论本身的问题,Ray-Kirchhoff积分的应用受到焦散等非正则区和多传播路径的限制。近年来,为了克服这些问题,出现了若干利用高斯波束叠加替代零阶几何射线理论表示Green函数的研究工作,极大地扩展了Kirchhoff积分的应用范围。在本文中,将利用高斯波束叠加Green函数的Kirchhoff积分理论称为Beam-Kirchhoff积分理论。
与Kirchhoff积分起源于光学不同,Born近似起源于量子力学,由德国物理学家、诺贝尔奖金获得者Max Born[1, 9]于1933年在研究量子散射问题时所提出。与Kirchhoff积分在地球物理中的应用历史类似,Born近似理论的应用也是为了解决地震波的传播、散射、数值模拟、偏移成像及反演等理论和技术问题[13, 31, 42, 90-93]。最初,在利用Born近似解决地球物理场数值模拟与反演成像问题时,用的是均匀背景介质和精确Green函数。到了20世纪80年代,随着所研究问题复杂程度的增加,零阶几何射线理论被用于表示Green函数[6, 34-36, 94]。在新世纪到来之时,高斯波束被引入到Born近似当中,形成了基于高斯波束叠加的Born近似理论,并先后被用于建立广义绕射叠加理论、最小二乘偏移、多次波偏移和全波形反演[42-43]。为了简便起见,在下文中将这种基于高斯波束叠加的Born近似理论称为Beam-Born理论。与Kirchhoff积分的发展和应用过程一样,在经过了几十年的研究之后,通过对几何射线理论和高斯波束叠加理论的应用,在地球物理数值模拟和反演成像领域中不但已经建立了完整的Ray-Born和Beam-Born理论,而且还提出了若干关于地震波传播的定理和公式,极大地丰富了地震波传播与散射高频渐近理论的内涵[51, 76, 95]。此外,对Born近似研究的另一个重要进展是将其与Kirchhoff积分联系在一起,消除了面积分理论和体积分理论之间的不一致问题,为建立统一的散射理论打下了基础[64]。
对于起源于无线电物理的Rytov近似,其在地球物理中的应用和发展历程与Born近似的应用和发展历程基本一样,也是从均匀背景介质和精确Green函数发展到基于零阶几何射线理论的Ray-Rytov形式。唯一的不同是应用领域。到目前为止,Rytov近似主要用于地球物理层析成像、走时反演和速度反演等等[24, 48-50]。近年来,Rytov近似也被用于模拟起伏界面和起伏海面对地震波的散射响应[96]。此外,早在20世纪80年代就已经证明,Born和Rytov之间存在函数关系[23]。2006年,Marks[97]提出了一种混合级数法,将Born和Rytov作为相应级数的极限情况,彻底地解决了Born和Rytov之间的关系问题。然而,Marks只讨论了标量波的情况。对于矢量波,笔者还没有见到类似的报道。
2.4 程函方程及其数值分析程函方程是非线性偏微分方程,到目前为止只能通过下列两条途径求解:1)根据特征理论求出渐近(射线)级数解(Lunerbur-Kline展开);2)根据数值分析原理求出数值解。对于前者,在具体应用时首先要进行射线追踪,确定射线路径;其次是计算射线走时,即沿射线路径对慢度进行积分;最后是计算射线振幅。在这个过程中,关键是如何能快速地计算出射线路径和射线方向。对于后者,首先是要选择一个合适的数值分析方案,准确快速地计算出走时;其次是选择一个稳定的数值求导方法,根据走时计算出射线路径和射线方向。在这个过程中,关键是如何能求出满足Fermat原理的最小走时以及如何能快速稳定地完成对走时的求导运算。因此,除了对上述一些理论问题所进行的长期深入研究之外,为了使Kirchhoff、Born和Rytov近似能够用于解决实际的生产问题,学术界和工业界的研究与开发工作者从20世纪80年代开始对几何射线Green函数的快速计算问题以及对于程函方程的有限差分数值分析问题进行了深入持久的研究。作为这种研究的结果,出现了一批计算射线路径和射线走时的新方法,例如有限差分法、波前构建法和快速推进法等等[98-105]。近年来,又出现了起伏地表条件下的迎风有限差分法和不等距有限差分法等新方法[106]。同时,寂静了多年的高斯波束计算方法研究也有了新的进展。在传统的计算方法中,需要在射线中心基坐标系中利用“Lagrangian”方法计算高斯波束,而在叠加时要利用全局慢度坐标系;因此,在计算过程中要不断地进行各种坐标变换[10]。2000年,Leung等[107]发表了关于Eulerian高斯波束叠加的工作成果,可以直接在直角坐标系中实现高斯波束的计算和叠加。然而,由于采用了水平集算法(level set method,或译为等值面函数法),使得Eulerian高斯波束叠加法需要在高于三维的空间内求解由刘维尔定理所导出的一系列方程,因此增加了计算量。此外,对高斯波束进行快速计算的另一个进展是利用数值方法求解复程函方程[108]。近年来,笔者所领导的研究组对这个问题进行了深入持久的研究,取得了初步的研究结果,得到了有关学术期刊的关注[51]。
3 若干新进展本节介绍笔者在最近5年内所取得的一些与高频渐近散射理论及其在地球物理场数值模拟与反演成像中应用有关的一些新进展,包括对面积分表示定理的拟解析近似、广义Beam-Born近似、Beam-Rytov近似和广义Beam-Rytov近似、弱散射近似所引入的误差以及任意函数与delta波包之间的褶积计算等等。
3.1 面积分方程的拟解析近似根据文献[26]和[27],拟解析近似是一种解积分方程的解析近似法,到目前为止主要用于构造体积分方程的近似解。尽管如此,拟解析近似的基本思想却与积分方程定义域的维数无关,从而也可以被用于解决面积分方程和线积分方程的近似解构造问题。在下文中,主要讨论如何建立基于面积分表示定理的反射波拟解析近似问题,而对于透射波和边缘绕射波的拟解析近似问题可以通过类似的途径给予解决。
根据面积分表示定理(方程(26)),反射场UR(r, ω)=U(r, ω)-Uin(r, ω)的形式积分解为
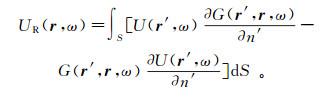 (52)
(52) 式中:U(r′, ω)是反射面S上的总场;G(r′, r, ω)是Green函数,其源点在r′。为了求出UR(r, ω),将式(52)归化到S上,得到下列积分方程[23]:
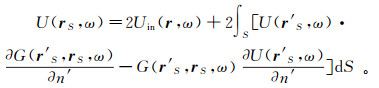 (53)
(53) 式中,下标S强调所标识的量是在反射面S上。
根据叠加原理,将U(r′S, ω)写成U(r′S, ω)=[Rc(r′S)+Λ(r′S)]Uin(r′S, ω)的形式。式中:Rc(r′S)是平面波反射系数;Λ(r′S)是反射函数;Uin(r′S, ω)是入射场。在物理上,Λ(r′S)的作用是校正局部平面波近似和切平面近似所带来的误差。根据文献[88]和[89],Rc(r′S)Uin(r′S, ω)代表界面上总场的主体部分,而Λ(r′S)Uin(r′S, ω)代表界面上总场的次要部分。换句话说,因子Rc(r′S)·Uin(r′S, ω)描述反射效应,而因子Λ(r′S)Uin(r′S, ω)描述无法被反射效应所包含的其他波动效应。因此,相对于Rc(r′S)来讲,Λ(r′S)是小量,所以可以被视为是r′S的缓变函数。
在式(53)中引入几何光学近似,有U(rS, ω)=in(rS, ω)+UR1(rS, ω)+UR2(rS, ω)。式中:in(rS, ω)=2UinRay(rS, ω),UinRay(rS, ω)是Uin(rS, ω)的几何光学近似;UR1(rS, ω)=IS1(rS, ω);UR2(rS, ω)=IS2(rS, ω)。其中:
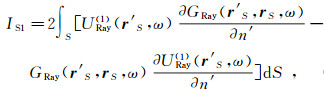 (54)
(54) 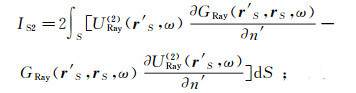 (55)
(55) 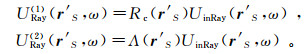 (56)
(56) 由于Rc(r′S)是已知函数,所以UR1(rS, ω)为已知,问题归结为求UR2(rS, ω)。为了得到UR2(rS, ω),首先将U(rS, ω)-Uin(rS, ω)和UR2(rS, ω)分别写为Rc(rS)UinRay(rS, ω)和Λ(rS)·UinRay(rS, ω)的形式;然后再将式(55)右端积分号内的Λ(r′S)替换为Λ(rS);最后得到
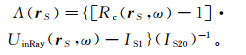 (57)
(57) 式中,
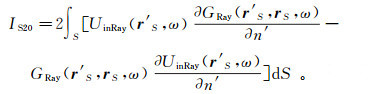 (58)
(58) 如果对积分IS1和IS20做稳相分析[88-89],则有IS1~2Rc(rS, ω)UinRay(rS, ω),IS20~2UinRay(rS, ω)。从而,Λ(rS)~-(Rc+1)/2。
在实际的实现过程中,为了便于计算,可以根据文献[64]将IS1和IS20转换为等时面叠加。由于篇幅的限制,在此略去IS1和IS20的等时面叠加形式。另外,如果令U(0)(rS, ω)=2Uin(rS, ω),则可构造方程(53)的Neumann级数解U(rS, ω)=U(0)(rS, ω)+∑n=1∞U(n)(rS, ω),U(n)(rS, ω)=2IS[U(n-1)(rS, ω)];式中,IS是方程(53)中的面积分算子。进一步,如果令U(0)(rS, ω)=RcUin(rS, ω),则可构造方程(53)的修正Neumann级数解。考虑到篇幅的限制,在此略去对这些级数解的讨论。
3.2 基于高斯波束和高斯波包叠加的高频渐近散射理论如上所述,到目前为止,在Kirchhoff和Born近似理论中已经采用了高斯波束叠加替代几何光学近似(零阶射线近似),进而解决了焦散区内场强分布的计算问题。然而,在公开发表的文献中还没有见到基于高斯波束叠加的广义Born近似和Rytov近似,也没有类似于广义Born近似的广义Rytov近似。另外,对于所有上述理论,还没有建立基于delta波包叠加的时间域形式。因此,需要对这些问题进行研究和探讨。
为了方便起见,在下文中将基于高斯波束和高斯波包的常规散射近似分别称为Beam-Born和Beam-Rytov近似,而将基于高斯波束和高斯波包的广义散射近似分别称为GBeam-Born和GBeam-Rytov近似,而不再区分波束和波包。这里,G代表Generalized。此外,为了节省篇幅和简便起见,只给出基于高斯波束叠加的数学公式。为了得到基于delta波包的表达式,只需将高斯波束叠加替换为delta波包叠加,而将相应的乘积替换为褶积即可。
3.2.1 GBeam-Born近似为了利用建立GBeam-Born近似,首先将高斯波束(波包)由基于中心射线的局部坐标变换到全局坐标,并将相应的叠加积分由球坐标(或慢度平面)转变到直角坐标。由于在本问题中积分运算和微分运算的次序是可交换的,所以在具体的推导过程中可以只考虑依附于一条给定中心射线的高斯波束。关于具体的变换公式,可参见文献[109]。
对于所考虑的高斯波束uGB(s, q, θ, φ)=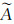
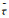
 (59)
(59) 式中:rs代表源点坐标;r代表观察点坐标;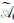
在外观上,公式(59)与几何光学(零阶射线)近似完全相同。所满足的程函方程和输运方程在外观上也完全一样。从而,如果用高斯波束叠加表示Green函数,有
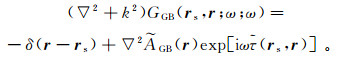 (60)
(60) 式中,k2=ω2p2(r)。
利用式(60)和式(10),得到
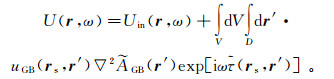 (61a)
(61a) 式中,D是在直角坐标系中给出的叠加区域。
如果密度为坐标的点函数,则有
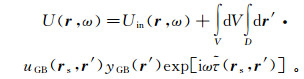 (61b)
(61b) 式中,yGB(r′)=[∇2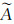
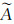
利用关系式dV=dΣIdnI=dΣIdτ/|∇r′τ,可以将式(61b)转换成为等时面叠加,即
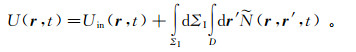 (62)
(62) 式中: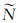
Beam-Rytov与Ray-Rytov的建立过程完全相同。因此,这里只给出相应的基本思想,具体推导过程见文献[23, p. 488]。
假设总场为U(r, ω)=exp[iψ(r)]。其中,ψ(r)=ψ0(r)+ψ1(r)。令背景场和散射场分别为U0(r, ω)=eiψ0(r)和U1(r, ω)=eiψ1(r)。利用方程(46)—(49),将U0(r, ω)及Green函数表示成为高斯波束叠加,得到
 (63)
(63) 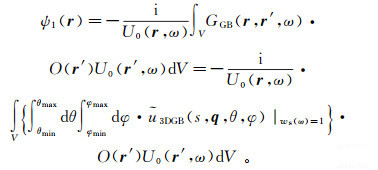 (64)
(64) 现在考虑GBeam-Rytov近似。根据Coates和Chapmand在1991年所提出的基本思想,在GBeam-Rytov近似中不进行介质和波场拆分。为了能得到相应的近似公式,引入已知波场Uin(r, ω),使得∇2Uin(r, ω)+k2(r)Uin(r, ω)=0。借鉴文献[23, p. 488] ]的推导过程,首先将总场U(r, ω)=eiψ(r)代入到波动方程(10)中,并令ws(rs, ω)=0;然后在由此导出方程i∇2ψ(r)-|∇ψ(r)|2+k2(r)=0的左右两端分别乘上-iUin(r, ω),得到
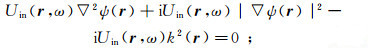 (65)
(65) 最后利用恒等式∇2[φ(r)ψ(r)]≡ψ(r)∇2φ(r)+φ(r)∇2ψ(r)+2∇φ(r)·∇ψ(r)进行一些整理,得到(注意∇2Uin(r, ω)=-k2(r)Uin(r, ω))
 (66)
(66) 式中, Y(r, ω)=Uin(r, ω)∇2ψ(r)+2∇Uin(r, ω)·∇ψ(r)。利用方程(65),得到∇2ψ(r)=ik2(r)-i|∇ψ(r)|2。利用这个公式和∇Uin(r, ω)=iUin(r, ω)∇ψ0(r),得到Y(r, ω)=iUin(r, ω)·{k2(r)-|∇ψ(r)|2+2∇ψ0(r)·∇ψ(r)}。进一步,令复相位函数ψ(r)为已知复相位ψ0(r)和未知复相位ψ1(r)的叠加,即ψ(r)=ψ0(r)+ψ1(r)。假设|ψ1(r)|2~0,则得到2∇ψ0(r)·∇ψ1(r)-|∇ψ(r)|2=-|∇ψ0(r)|2-|∇1ψ(r)|2的弱散射近似,即2∇ψ0(r)·∇ψ1(r)-|∇ψ(r)|2=-|∇0ψ(r)|2。因此,
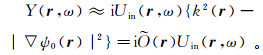 (67)
(67) 式中,(r)=k2(r)-|∇ψ0(r)|2。
在公式(67)中,所有的函数均为已知。从而,利用第二Green定理得到
 (68)
(68) 这就是广义Rytov近似的一般表达式。
在外观上,广义Rytov近似式(68)和经典Rytov近似式(35)的差别只是将O(r)置换为(r);然而,在这两个公式之间却有着实质性的差别。对于公式(68),在其建立过程中的唯一近似是假设|ψ1(r)|2~0,既没有介质拆分也没有场拆分;因此,U0(r, ω)=eiψ0(r)和U1(r, ω)=eiψ1(r)均具有唯一性,是具有物理意义的入射场和散射场,而非形式上或数学上的入射场和散射场。
在实际应用中,公式(68)中的入射场Uin(r, ω)(Uin(r′, ω))和Green函数G(r′, r, ω)均可以采取多种途径进行计算:如果利用URay(r, ω)(方程(25))和GRay(r, r′, ω)(方程(45))计算,则得到广义的Ray-Rytov近似,简称为GRay-Rytov近似;如果利用UGB(r, ω)(方程(48))和GGB(r, r′, ω)(方程(49))计算,则得到GBeam-Rytov近似;如果采用方程(40)所描述的Green函数,则得到与Coates和Champman的广义Born近似类似的广义Rytov形式积分解,即
 (69)
(69) 方程(68)是一个关于ψ1(r)的积分方程。令其右端的第一项为ψ1(0)(r),则可以构造Neumann级数解ψ1(r)=ψ1(0)(r)+ψ1(1)(r)+ψ1(2)(r)+…。其中,
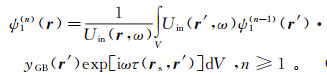 (70)
(70) 利用关系式dV=dΣIdnI=dΣIdτ/|∇r′τ|,可以将式(64)、式(68)和式(69)转换成为等时面叠加。考虑到篇幅的限制,此处略去相应公式。有兴趣的读者可以参见文献[54]和[64]。
3.3 基于零阶射线和高斯波束叠加的混合级数理论本节的目的是将Marks提出的混合近似理论[97]扩展到非均匀背景介质,建立基于射线理论的Ray-Hybrid近似(Ray-Hybrid approximation)和基于高斯波束叠加的Beam-Hybrid近似(Beam-Hybrid approximation)及GHybrid近似(generalized Hybrid approximation),包括GRay-Hybrid和GBeam-Hybrid近似。如果将高斯波束叠加置换为delta波包叠加,则得到时间域混合近似。
首先考虑基于介质和波场拆分的扩展。根据Marks文[97]中的公式(4),假设非均匀介质中的波场具有下列形式的试探解:
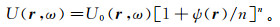 (71)
(71) 式中:Uin(r, ω)是背景介质中的场,满足方程[∇2+k02(r)]Uin(r, ω)=0;ψ(r)是复相位,ψ(r)=Σm=0∞χmψm(r);χm是一个确定近似阶数的参数(order parametr)。另外,由于在背景介质中U(r, ω)=Uin(r),所以ψ0(r)=0。再有,n是位于[1, ∞)中的参数:当n=1时,U(r, ω)=Uin(r, ω)+Uin(r, ω)·ψ(r),以Born型近似为极限;当n→∞时,U(r, ω)=Uin(r, ω)eψ(r),以Rytov型近似为极限[97]。
将式(71)带入到波动方程[∇2+k2(r)]U(r, ω)=0,得到一个与文献[97]中的方程(5)在外观上完全一样的方程,即
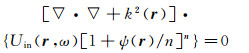 (72)
(72) 对方程(72)进行一些整理,得到文献[97]中的方程(6)(8),并最终得到
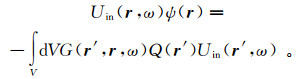 (73)
(73) 其中,
 (74)
(74) 式中,O(r)=k2(r)-k02(r)。
对式(74)进行线性化(只保留关于χ的线性项)得到
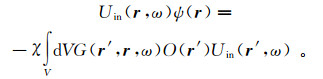 (75)
(75) 类似地,还可以得到基于几何光学近似URay(r′, ω)和GRay(r′, r, ω)的高阶近似。
公式(73)和(75)与Marks文中的有关公式在形式上完全相同;其差别仅在于这里的入射场Uin(r′, ω)和Green函数G(r′, r, ω)是几何光学场或高斯波束叠加,而在Marks的原文中Uin(r′, ω)和G(r′, r, ω)是均匀介质中的精确解。
现在考虑不对介质和波场进行拆分的广义近似。借鉴建立广义Rytov近似时所采用的方法,得到
 (76)
(76) 式中,Q(r)由公式(74)给出。
利用方程(40),得到
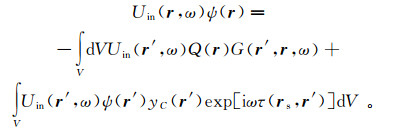 (77)
(77) 式中:yC(r′)=[∇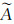
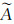
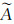
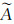
公式(77)是一个关于ψ(r)的形式积分解。如果将观察点r置于散射体V内,则可将其转化成为一个关于ψ1(r)的体积分方程。为了得到这个方程的Neumann级数解,可直接在方程(70)中将ψ1(r)置换为ψ(r)。考虑到篇幅的限制,在此略去ψ(r)的Neumann级数解ψ(r)=ψ(0)(r)+ψ(1)(r)+…中各级近似的具体表达式。
3.4 弱散射近似所带来的误差反演理论中的一个基本问题是:我们到底能反演什么?如果我们采用Born型或Rytov型近似,所得到的输出结果到底是什么?对于这个问题,Slaney等[110]早在1984年对医学CT的研究中就做过讨论。据此,现在讨论在地球物理反演中应用弱散射理论所带来的误差。
根据方程(30),散射场的形式积分解为
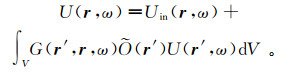 (78)
(78) 令
 (79)
(79) 如果


 (80)
(80) 进一步,令U(r, ω)≈A(r)exp[iωτ(r)],Uin(r, ω)=Ain(r)exp[iωτin(r)]。则,
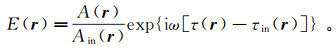 (81)
(81) 其中:A(r)/Ain(r)代表振幅误差;τ(r)-τin(r)代表相位误差。一般来讲,相对于成像来讲,振幅误差相对于相位误差起到的是次一级的作用。因此,对于偏移成像,采用弱散射近似的误差主要是由时差τ(r)-τin(r)带来的位置误差;对于全波形反演成像,采用弱散射近似既有τ(r)-τin(r)带来的位置误差,又有A(r)/Ain(r)带来的振幅误差。
如果对总场U(r, ω)和入射场Uin(r, ω)均采用精度高于几何光学场的近似,则U(r, ω)=|U(r, ω)|eiarg[U(r, ω)];Uin(r, ω)=|Uin(r, ω)|eiarg[Uin(r, ω)]。式中,arg(z)代表z的辐角。从而,弱散射近似带来的误差为
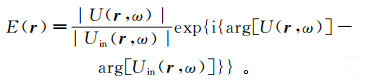 (82)
(82) 其中,|U(r, ω)|/|Uin(r, ω)|是振幅误差;arg[U(r, ω)]-argUin(r, ω)是相位误差。
3.5 任意函数与delta波包之间的褶积计算在利用delta波包叠加表示时间-空间域中的Green函数时,要遇到形如
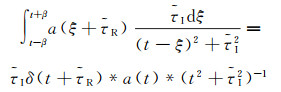 (83)
(83) 的积分。在具体的实现过程中,这个积分将导致对积分限的反复判断和若干重复计算。为了避免这些问题,可以对a(t)进行Taylor展开,并利用文献[111]中给出的不定积分公式,得到
 (84a)
(84a) 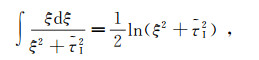 (84b)
(84b) 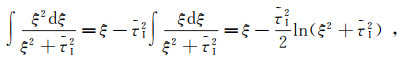 (84c)
(84c) 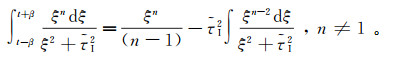 (84d)
(84d) 利用公式(84),可以求出由公式(83)所给出的褶积。根据文献[112]中的有关研究,利用公式(84a)即可以得到满意的结果。
4 总结和展望高频渐近散射理论主要由几何射线级数理论(简称为ART, 又称为Luneburg-Kline展开)、几何绕射理论(Keller理论,简称为GTD)、物理绕射理论(Umfimtsev(Уфимицев)理论,简称为PTD)、Kirchhoff型积分近似、Born型(级数)近似、Rytov型(级数)以及拟解析近似等若干种方法组成。其中,几何射线级数是波动方程或运动方程关于频率倒数的渐近级数解,其本身就具有高频近似的特点。同样的结论对于几何绕射理论、物理绕射理论和Kirchhoff近似也成立。然而,对于Born近似和Rytov近似,其初衷均是在Green函数为严格已知的前提下对散射波进行近似;因此,就其本身来讲并不具有高频渐近的特点。之所以将这两种方法划入高频渐近散射理论,是因为在非均匀介质中的远区只能对Green函数进行高频近似。一旦应用了高频渐近Green函数,原本不具有高频近似特点的Born型和Rytov型近似就变成了高频近似方法。
在历史上,最早在地球物理中得到应用的高频渐近波动理论是几何射线理论,其次是Kirchhoff型近似理论,最后是Born型和Rytov型近似理论。这主要是因为在早期的地球物理发展中,所关注的观测量是时间而非振幅,而所关注的波动过程是反射和透射,而非散射。在与地球物理有关的数字化革命期间(20世纪6070年代),Kirchhoff型积分在地震学、反射地震学以及地球电磁学中得到了广泛的应用。到了20世纪80年代,随着医学CT理论在地球物理中的移植和推广,Born型和Rytov型近似逐渐被广大地球物理研究者所熟悉。今天,基于Kirchhoff型、Born型和Rytov型近似的地球物理场数值模拟与反演成像理论已经对地球物理的发展产生了深远的影响,形成了诸如Kirchhoff型数值模拟理论、Kirchhoff型(真振幅)反射地震(偏移与反偏移)成像理论、Born型数值模拟理论、Born型偏移和反偏移理论、Born型广义绕射叠加偏移理论、Rytov型偏移理论以及基于Kirchhoff型、Born型和Rytov型积分算子的地球物理场反演理论。然而,所有这些成就的取得均得益于对高频渐近Green函数的应用;换句话说,均得益于对几何光学(零阶几何射线)近似以及高斯波束叠加近似的应用。可以毫不夸张地讲,对Green函数射线类近似的应用是建立上述理论和导致上述理论在理论研究和工业应用中获得巨大成功的关键所在;同样,对Green函数射线类近似的应用也是导致上述理论在强不均匀介质中失效的关键所在。因此,在今后的发展过程中,对高频渐近Green函数的研究将是推动高频渐近散射理论发展的关键所在。笔者认为,对高频渐近Green函数的研究包括:一方面是数学表达形式,另一方面是相应的快速计算技术。事实上,只有通过对数学表达形式的改进才能拓宽高频渐近Green函数的有效范围和提高对介质非均匀程度的适应能力;而只有发展快速计算技术才能将有关数学理论转化为工业应用,两者缺一不可。
高频渐近散射理论除了具有丰富的数学物理内涵之外,在地球物理场数值模拟和反演成像方面也有异常广泛的应用。因此,不可能指望在一篇文章中对高频渐近散射理论及其在地球物理场数值模拟和反演成像中的应用进行面面俱到的综述和评论。考虑到这一点,笔者在本文中只对一些具有里程碑意义的进展和成果进行了有选择的介绍和评述。但愿这种选择不会引起重大的遗漏和误导。
除了对一些具有里程碑意义的进展和成果进行介绍和评述之外,本文还扼要地介绍了笔者在近5年内所取得的一些与高频渐近散射理论有关的研究进展,包括对面积分方程的拟解析近似、GBeam-Born型近似、GBeam-Rytov型近似、弱散射近似所带来的误差、混合级数近似理论和任意函数与delta波包的褶积计算等等。笔者期望,这些进展能够在某种程度上丰富高频渐近散射理论的内涵,并使其能在地球物理场数值模拟与反演成像中得到更多的应用。
最后,笔者认为,对于高频渐近散射理论本身的改进在于找到比几何光学近似和高斯波束叠加更好的Green函数表达,而对于高频渐近散射理论在应用方面的改进在于寻找更合适的快速计算技术。对于高频渐近散射理论在地球物理场数值模拟和反演成像中的应用来讲,两者缺一不可。
| [1] | Born M, Wolf E. Principles of Optics. Principles of Optics6th ed [M]. New York: Pergamon Press, 1980 . |
| [2] | Bowman J J, Senior T B A, Uslenghi P L E. Electromagnetic and Acoustic Scattering by Simple Shapes [M]. Amsterdam: North-Holland, 1969 . |
| [3] | Felsen L B, Marcuvitz. Radiation and Scattering of Waves [M]. Englewood Cliffs: Prentice-Hall, 1973 . |
| [4] | Hecht E. Optics. Beijing[M]. [S.l.]: Higher Education Press, 2005. |
| [5] | Ishimaru A. Electromagnetic Waves Propagation, Radiation, and Scattering [M]. Englewood Cliffs: Prentice-Hall, 1991 . |
| [6] | Kline M, Kay I W. Electromagnetic Theory and Geometrical Optics [M]. New York: Interscience, 1965 . |
| [7] | Kravtsov Yu A, Orlov Yu I. Geometrical Optics of Inhomogeneous Media [M]. Berlin: Springer-Verlag, 1990 . |
| [8] | Mcnamara D A, Pistorius C W I, Malherbe J A G. Introduction to the Uniform Geometrical Theory of Diffraction [M]. Norwood: Artech House, 1990 . |
| [9] | Born M, Wolf E. Principles of Optics: Volumes 1 and 27th ed [M]. Beijing: Publishing House of Electronics Industry, 2006 . |
| [10] | ČervenýV. Seismic Ray Theory [M]. Cambridge: Cambridge University Press, 2001 . |
| [11] | 李永俊. 电磁理论的高频方法 [M]. 武汉: 武汉大学出版社, 1999 . Li Yongjun. High-Frequency Methods of Electromagnetic Theory [M]. Wuhan: Wuhan University Press, 1999 . |
| [12] | 汪茂光. 几何绕射理论(2版 ) [M]. 西安: 西安电子科技大学出版社, 1994 . Wang Maoguang. Geometrical Theory of Diffraction [M]. Xi'an: Xi Dian University Press, 1994 . |
| [13] | Coates R T, Chapman C H. Generalized Born Scattering of Elastic Waves in 3-D Media[J]. Geophysical Journal International , 1991, 107 : 231-263. |
| [14] | Senior T B A, Uslenghi P L E. Experimental Detection of the Edge-Diffracted Cone[J]. Proceedings of the IEEE , 1972, 60 (11) : 1448. |
| [15] | Luneburg R K. Mathematical Theory of Optics [M]. Berkley: University of California Press, 1964 . |
| [16] | Aki K, Richards P G. Quantitative Seismology Theory and Methods: Volume 1 and 2 [M]. San Francisco: W H Freeman and Co, 1980 . |
| [17] | Keller J B. Geometrical Acoustics: I: The Theory of Weak Shock Waves[J]. Journal of Applied Physics , 1954, 25 (8) : 116-130. |
| [18] | 长春地质学院, 成都地质学院, 武汉地质学院合编. 地震勘探:原理和方法 [M]. 北京: 地质出版社, 1980 . Compiled By Changchun College of Geology, Chengdu College of Geology, and Wuhan College of Geology. Seismic Exploration: Principles and Methods [M]. Beijing: Geological Publishing House, 1980 . |
| [19] | Keller J B. Geometrical Theory of Diffraction[J]. Jo-urnal of Optical Society of America , 1962, 52 : 116-130. DOI:10.1364/JOSA.52.000116 |
| [20] | Karal F G, Keller J B. Elastic Wave Propagation in Homogeneous and Inhomogeneous Media[J]. Journal of Acoustic Society of American , 1959, 3 : 694-705. |
| [21] | Goodman J W. Roberts and Company Publishers3rd ed [M]. Introduction to Fourier Optics, 2005 . |
| [22] | Hill R. Prestack Gaussian-Beam Depth Migration[J]. Geophysics , 2001, 66 (4) : 1240-1250. DOI:10.1190/1.1487071 |
| [23] | Chew W C. Waves and Fields in Inhomogeneous Media [M]. New York: Van Nostrand Reinhold, 1990 . |
| [24] | Devaney A J. Geophysical Diffraction Tomography[J]. IEEE Transactions on Geosciences and Remote Sensing , 1984, GE-22 : 1-13. |
| [25] | Stratton J A. Electromagnetic Theory[M]. [S. l. ]: Mcgraw-Hill Book Company, 1941. |
| [26] | 孙建国. 声波散射数值模拟的两种新方案[J]. 吉林大学学报(地球科学版) , 2006, 36 (5) : 863-868. Sun Jianguo. Two New Schemes for Numerical Mo-deling of Acoustic Scattering[J]. Journal of Jilin University (Earth Science Edition) , 2006, 36 (5) : 863-868. |
| [27] | Zhdanov M S, Dmitriev V I, Fang S, et al. Quasia-nalytical Approximations and Series in Electromagnetic Modeling[J]. Geophysics , 2000, 65 : 1746-1757. DOI:10.1190/1.1444859 |
| [28] | Zhdanov M S, Fang S. Three-Dimensional Quasi-Linear Electromagnetic Modeling and Inversion[M]//Oristaglio M, Spies B. Three-Dimensional Electromagnetics. Tulsa: Society of Exploration Geophysicists, 1999: 233-255. |
| [29] | Zhdanov M S, Fang S, Hurs'An G. Electromagnetic Inversion Using Quasi-Linear Approximation[J]. Geophysics , 2000, 65 : 1501-1513. DOI:10.1190/1.1444839 |
| [30] | Zhdanov M S, Tartaras E. Three-Dimensional Inversion of Multitransmitter Electromagnetic Data Based on the Localized Quasilinear Approximation[J]. Geophysical Journal International , 2002, 148 : 506-519. DOI:10.1046/j.1365-246x.2002.01591.x |
| [31] | Beylkin G. Imaging of Discontinuities in the Inverse Scattering Problem by Inversion of a Causal Generalized Radon Transform[J]. Journal of Mathematical Physics , 1985, 26 : 99-108. DOI:10.1063/1.526755 |
| [32] | Beylkin G. Mathematical Theory for Seismic Migration and Spatial Resolution[M]// Worthington M H. Deconvolution and Inversion. Oxford: Blackwell Scientific Publications, 1987, 291-304. |
| [33] | 仇庆玖, 陈恕行, 是嘉鸿, 等. 傅里叶积分算子及其应用 [M]. 北京: 科学出版社, 1985 . Qiu Qingjiu, Chen Shuxing, Shi Jiahong, et al. The Fourier Integral Operator and Its Applications [M]. Beijing: Science Press, 1985 . |
| [34] | Bleistein N, Gray S H. An Extension of the Born Inversion Method to a Depth Dependent Reference Profile[J]. Geophysical Prospecting , 1985, 33 : 999-1022. DOI:10.1111/gpr.1985.33.issue-7 |
| [35] | Bleistein N. On the Imaging of Reflectors in the Earth[J]. Geophysics , 1987, 52 : 931-942. DOI:10.1190/1.1442363 |
| [36] | Bleistein N, Cohen J K, Hagin F G. Two and One-Half Dimensional Born Inversion with an Arbitrary Reference[J]. Geophysics , 1987, 52 : 26-36. DOI:10.1190/1.1442238 |
| [37] | Bleistein N, Cohen J K, Stockwell J W. Mathematics of Multidimensional Seismic Imaging Migration, and Inversion [M]. New York: Springer-Verlag, 2001 . |
| [38] | LambarÉG. Sterotomography[J]. Geophysics , 2003, 73 (5) : VE25-VE34. |
| [39] | Schleicher J, Tygel M, Hubral P. Seismic True-Amplitude Imaging. SEG [M]. 2007 . |
| [40] | Wapenaar C P A, Berkhout A J. Springer-Verlag [M]. Amsterdam: Elsevier, 1989 . |
| [41] | Zhdanov M S. Integral Transforms in Geophysics [M]. Berlin: Springer, 1988 . |
| [42] | Virieux J, Operto S. An Overview of Full-Waveform Inversion in Exploration Geophysics[J]. Geophysics , 2009, 74 (6) : WCC127-WCC152. DOI:10.1190/1.3237087 |
| [43] | Etgen J, Gray S H, Zhang Y. An Overview of Depth Imaging in Exploration Geophysics[J]. Geophysics , 2009, 74 (6) : WCA5-WCA17. DOI:10.1190/1.3223188 |
| [44] | Thierry P G, Lambaré P, Podvin, et al. 3-D Preserved Amplitude Prestack Depth Migration on a Workstation[J]. Geophysics , 1999, 64 : 222-229. DOI:10.1190/1.1444518 |
| [45] | Thierry P, Operto S, Lambar G. Fast 2D Ray-Born Inversion/Migration in Complex Media[J]. Geophysics , 1999, 64 : 62-181. |
| [46] | Schuster G T. Reverse-Time Migration=Generalized Diffraction Stack Migration[C]// Abstract of SEG Annual Meeting. Houston: SEG, 2009: 1280-1283. |
| [47] | Zhan G, Dai W, Zhou M, et al. Generalized Diffraction-Stack Migration and Filtering of Coherent Noise[J]. Geophysical Prospecting , 2014, 62 : 1-16. DOI:10.1111/gpr.2014.62.issue-1 |
| [48] | Sun H, Schuster G T. 2-D Wave Path Migration[J]. Geophysics , 2001, 66 : 1528-1537. DOI:10.1190/1.1487099 |
| [49] | Woodward M J. Wave-Equation Tomography[J]. Geophysics , 1992, 57 : 15-26. DOI:10.1190/1.1443179 |
| [50] | Woodward M J, Nichols D, Zdraveva O, et al. A Decade of Tomography[J]. Geophysics , 2008, 73 (5) : VE5-VE11. DOI:10.1190/1.2969907 |
| [51] | Ursin B, Tygel M. Reciprocal Volume and Surface Scattering Integrals for Anisotropic Elastic Media[J]. Wave Motion , 1997, 26 : 31-42. DOI:10.1016/S0165-2125(97)00015-2 |
| [52] | Schleicher J, Tygel M, Ursin B, et al. The Kirchhoff-Helmholtz Integral for Anisotropic Elastic Media[J]. Wave Motion , 2001, 34 : 353-364. DOI:10.1016/S0165-2125(01)00077-4 |
| [53] | Tygel M, Schleicher J, Hubral P. The Kirchhoff-Helmholtz Integral Pair[J]. Journal of Computational Acoustics , 2001, 9 (4) : 1383. |
| [54] | Huang X, Sun H, Sun J. Born Modeling for Heterogeneous Media Using the Gaussian Beam Summation Based Green's Function[J]. Journal of Applied Geophysics , 2016, 131 : 191-201. DOI:10.1016/j.jappgeo.2016.06.004 |
| [55] | Huang X, Sun J, Sun Z. Local Algorithm for Computing Complex Travel Time Based on the Complex Eikonal Equation[J]. Physical Review E , 2016, 93 (4) : 043307. DOI:10.1103/PhysRevE.93.043307 |
| [56] | Berkhout A J, Verschuur D J. Full Wavefield Migration, Utilizing Surface and Internal Multiple Scattering[C]// Abstract of SEG Annual Meeting. San Antonio: SEG, 2011: 3212-3215. |
| [57] | Davydenko M, Verschuur D J. Full Wavefield Migration, Using Internal Multiples for Undershooting[C]// Abstract of SEG Annual Meeting. Houston: SEG, 2013: 3741-3744. |
| [58] | Weglein A B. Multiples: Signal or Noise?[C]// Abstract of SEG Annual Meeting. Denver: SEG, 2014: 4393-4398. |
| [59] | Weglein A B. Multiples Can Be Useful (at Times) to Enhance Imaging, by Providing an Approximate Image of an Unrecorded Primary, But Its Always Primaries That Are Migrated or Imaged[C]//Abstract of SEG Annual Meeting. New Orleans: SEG, 2015:4033-4037. |
| [60] | 朗道, 栗夫席兹. 理论物理学教程:第三卷:量子力学(非相对论部分)(6版 ) [M]. 北京: 高等教育出版社, 2008 . Landau L D, Lifshits E M. Theoretical Physics:III. Quantum Mechanics (Non-Relativity Theory6th ed [M]. Beijing: Higher Education Press, 2008 . |
| [61] | Mavko G, Mukerji T, Dvorikin J. The Rock Physics Handbook: Tools for Seismic Analysis in Porous Media [M]. Cambridge: Cambridge University Press, 1998 . |
| [62] | Bleistein N. Mathematical Methods for Wave Phenomena [M]. New York: Academic Press Inc, 1984 . |
| [63] | James G L. Geometrical Theory of Diffraction for Electromagnetic Waves [M]. Stevenage: Peter Peregrinus Ltd, 1976 . |
| [64] | Jaramillo H H, Bleistein N. The Link of Kirchhoff Migration and Demigration to Kirchhoff and Born Modeling[J]. Geophysics , 1999, 64 (6) : 1793-1805. DOI:10.1190/1.1444685 |
| [65] | Courant R, Hilbert D. Methods of Mathematical Phy-sicsVolume II [M]. New York: Wiley, 2008 . |
| [66] | Popov M M. A New Method of Computation of Wave Fields Using Gaussian Beams[J]. Wave Motion , 1982, 4 : 85-97. DOI:10.1016/0165-2125(82)90016-6 |
| [67] | Popov M M, Semtchenok N M, Popov P M, et al. Depth Migration by the Gaussian Beam Summation Method[J]. Geophysics , 2010, 75 (2) : S81-S93. DOI:10.1190/1.3361651 |
| [68] | Babich V M, Buldyrev V S. Short-Wavelength Diffraction Theory: Asymptotic Methods [M]. Berlin: Springer Verlag, 1990 . |
| [69] | Brekhovskikh L M. Waves in Layered Media [M]. Academic Press, 1960 . |
| [70] | Chapman C H, Drummond R. Body-Wave Seismograms in Inhomogeneous Media Using Maslov Asymptotic Theory[J]. Bulletin of the Seismological Society of America , 1982, 72 : S277-S317. |
| [71] | White S, Norris A, Bayliss A, Burridge R. Some Remarks on the Gaussian Beam Summation Method[J]. Geophys J R Astr Soc , 1987, 89 : 579-636. DOI:10.1111/j.1365-246X.1987.tb05184.x |
| [72] | Bortfeld R K. Geometrical Ray Theory: Rays and Traveltimes in Seismic Systems (Second-Order Approximation of the Traveltimes)[J]. Geophysics , 1989, 54 : 342-349. DOI:10.1190/1.1442659 |
| [73] | Hubral P, Schleicher J, Tygel M. Three-Dimensional Paraxial Ray Properties: I: Basic Relations[J]. Journal of Seismic Exploration , 1992, 1 : 265-279. |
| [74] | Hubral P, Schleicher J, Tygel M. Three-Dimensional Paraxial Ray Properties: II: Applications[J]. Journal of Seismic Exploration , 1992, 1 : 347-362. |
| [75] | Tygel M, Schleicher J, Hubral P. A Unified Approach in 3-D Seismic Reflection Imaging, Part II: Theory[J]. Geophysics , 1996, 61 (3) : 759-775. DOI:10.1190/1.1444002 |
| [76] | De Hoop M V, Bleistein N. Generalized Radon Transform Inversions for Reflectivity in Anisotropic Elastic Media[J]. Inverse Problems , 1997, 13 : 669-690. DOI:10.1088/0266-5611/13/3/009 |
| [77] | Alkhalifah T. Gaussian Beam Depth Migration for Anisotropic Media[J]. Geophysics , 1995, 60 (5) : 1474-1484. DOI:10.1190/1.1443881 |
| [78] | Albertin U, Yingst D, Kitchenside P. True Amplitude Beam Migration[C]// Abstract of SEG Annual Meeting. Denver: SEG, 2004: 398-401. |
| [79] | Gray S H, Bleistein N. True-Amplitude Gaussian-Beam Migration[J]. Geophysics , 2009, 74 (2) : S11-S23. DOI:10.1190/1.3052116 |
| [80] | Han J, Wang Y, Lu J. Multi-Component Gaussian Beam Prestack Depth Migration[J]. Journal of Geophysics and Engeneering , 2013, 10 : 1-10. |
| [81] | Hill N R. Prestack Gaussian-Beam Depth Migration[J]. Geophysics , 2001, 66 (4) : 1240-1250. DOI:10.1190/1.1487071 |
| [82] | Protasov M I, Tcheverda V A. True Amplitude Elastic Gaussian Beam Imaging of Multicomponent Walkaway Vertical Seismic Profiling Data[J]. Geophysical Prospecting , 2012, 60 : 1030-1042. DOI:10.1111/gpr.2012.60.issue-6 |
| [83] | Protasov M I, Tcheverda V A. True Amplitude Imaging by Inverse Generalized Radon Transform Based on Gaussian Beam Decomposition of the Acoustic Greenčs Function[J]. Geophysical Prospecting , 2011, 59 (2) : 197-209. DOI:10.1111/gpr.2011.59.issue-2 |
| [84] | ČervenýV, PšenčiK I. Gaussian Beams in Inhomogeneous Anisotropic Layered Structures[J]. Geophy-sical Journal International , 2010, 180 : 798-812. |
| [85] | ČervenýV. Synthetic Body Wave Seismograms for Laterally Varying Layered Structures by the Gaussian Beam Method[J]. Geophys J Roy Astr Soc , 1983, 73 : 389-426. |
| [86] | Frazer L N, Sen M K. Kirchhoff-Helmholtz Reflection Seismograms in a Laterally Inhomogeneous Multi-Layered Elastic Medium-I. Theory[J]. Geophys J R Astr Soc , 1985, 80 : 121-147. DOI:10.1111/gji.1985.80.issue-1 |
| [87] | Sen M K, Frazer L N. Kirchhoff-Helmholtz Reflection Seismograms in a Laterally Inhomogeneous Multi-Layered Elastic Medium: Part II: Computations[J]. Geophys J Roy Astr Soc , 1985, 82 : 415-437. DOI:10.1111/j.1365-246X.1985.tb05144.x |
| [88] | Sun J. The Relationship Between the First Fresnel Zone and the Normalized Geometrical Spreading Factor[J]. Geophysical Prospecting , 1996, 44 (3) : 351-374. DOI:10.1111/gpr.1996.44.issue-3 |
| [89] | Sun J. 3-D Crosswell Transmissions: Paraxial Ray Solutions and Reciprocity Paradox[J]. Geophysics , 1995, 60 (3) : 810-820. DOI:10.1190/1.1443819 |
| [90] | Cohen J K, Hagin F G, Bleistein N. Threedimensional Born Inversion with an Arbitrary Reference[J]. Geophysics , 1986, 51 : 1552-1558. DOI:10.1190/1.1442205 |
| [91] | Coates R T, Chapman C H. Ray Perturbation Theory and the Born Approximation[J]. Geophysical Journal International , 1990, 100 : 379-392. DOI:10.1111/gji.1990.100.issue-3 |
| [92] | Xu S, Lambar G. Fast Migration/Inversion with Multivalued Ray Fields: Part 1: Method, Validation Test, and Application in 2D to Marmousi[J]. Geophysics , 2004, 69 (5) : 1311-1319. DOI:10.1190/1.1801947 |
| [93] | Xu S, Chauris H, Lambaré G, Noble M. Common-Angle Migration: A Strategy for Imaging Complex Media[J]. Geophysics , 2001, 66 : 1877-1894. DOI:10.1190/1.1487131 |
| [94] | Miller D, Oristaglio M, Beylkin G. A New Slant on Seismic Imaging: Migration and Integral Geometry[J]. Geophysics , 1987, 52 (7) : 943-964. DOI:10.1190/1.1442364 |
| [95] | Tygel M, Ursin B. Weak-Contrast Edge and Vertex Diffractions in Anisotropic Elastic Media[J]. Wave Motion , 1999, 29 (4) : 363-373. DOI:10.1016/S0165-2125(98)00044-4 |
| [96] | Yu G X, Fu L Y. Rytov Series Approximation for Rough Surface Scattering[J]. Bulletin of the Seismological Society of America , 2012, 102 (1) : 42-52. DOI:10.1785/0120110083 |
| [97] | Marks D L. A Family of Approximations Spanning the Born and Rytov Scattering Series[J]. Optics Express , 2006, 14 (19) : 8837-8848. DOI:10.1364/OE.14.008837 |
| [98] | Vidale J. Finite-Difference Calculation of Travel Ti-mes[J]. Bulletin of the Seismological Society of America , 1988, 78 : 2062-2076. |
| [99] | Vinje V, Iversen E, Gjoystdal H. Traveltime and Amplitude Estimation Using Wavefront Construction[J]. Geophysics , 1993, 58 : 1157-1166. DOI:10.1190/1.1443499 |
| [100] | Sethian J A. A Fast Marching Level Set Method for Monotonically Advancing Fronts[J]. Proceedings of the National Academy of Sciences of the United States of America , 1996, 93 : 1591-1595. DOI:10.1073/pnas.93.4.1591 |
| [101] | Sethian J A. Fast Marching Methods[J]. SIAM Review , 1999, 41 : 199-235. DOI:10.1137/S0036144598347059 |
| [102] | Sethian J A. Evolution, Implementation, and Application of Level Set and Fast Marching Methods for Advancing Fronts[J]. Journal of Computational Physics , 2001, 169 : 503-555. DOI:10.1006/jcph.2000.6657 |
| [103] | Sethian J A, Popovici A M. 3-D Traveltime Computation Using the Fast Marching Method[J]. Geophysics , 1999, 64 : 516-523. DOI:10.1190/1.1444558 |
| [104] | Rawlinson N, Sambridge M. Multiple Reflection and Transmission Phases in Complex Layered Media Using a Multistage Fast Marching Method[J]. Geophysics , 2004, 69 : 1338-1350. DOI:10.1190/1.1801950 |
| [105] | Rawlinson N, Sambridge M. Wave Front Evolution in Strongly Heterogeneous Layered Media Using the Fast Marching Method[J]. Geophysical Journal International , 2004, 156 : 631-647. DOI:10.1111/gji.2004.156.issue-3 |
| [106] | Sun J, Sun Z, Han F. A Finite Difference Scheme for Solving the Eikonal Equation Including Surface Topography[J]. Geophysics , 2011, 76 (4) : T53-T63. DOI:10.1190/1.3580634 |
| [107] | Leung S, Qian J, Burridge R. Eulerian Gaussian Beams for High-Frequency Wave Propagation[J]. Geophysics , 2007, 72 (5) : SM61-SM76. DOI:10.1190/1.2752136 |
| [108] | Li S, Fomel S. Improving Wave-Equation Fidelity of Gaussian Beams by Solving the Complex Eikonal Equation[C]// Abstract of SEG Annual Meeting. San Antonio: SEG, 2011: 3829-3833. |
| [109] | Červený V. The Appliocation of Ray Tracing to the Propagation of Shear Waves in Complex Media[M]// Dohr G P. Seismic Share Waves. London: Geophysical Press, 1985: 1-124. |
| [110] | Slaney S M, Kak A C, Larsen L E. Limitations of Imaging with First-Order Diffraction Tomography[J]. IEEE Transactions on Microwave Theory and Techniques , 1984, MTT-32 : 860-874. |
| [111] | 《数学手册》编写组. 数学手册 [M]. 北京: 高等教育出版社, 1979 . Compile Group of Handbook of Mathematics. Handbook of Mathematics [M]. Beijing: Higher Education Press, 1979 . |
| [112] | 石秀林, 孙建国, 孙辉, 等. 基于Delta波包叠加的时间域深度偏移[J]. 地球物理学报 , 2016, 59 (7) : 2641-2649. Shi Xiulin, Sun Jianguo, Sun Hui, et al. The Time-Domain Depth Migration by the Summation of Delta Packets[J]. Chinese Journal of Geophysics , 2016, 59 (7) : 2641-2649. |


