0 引言
利用核磁共振(magnetic resonance sounding, MRS)技术探测地下水是20世纪80年代国际上发展起来的一种地球物理新方法[1]。过去几年,该技术在正演模型[2]和反演解释[3-5]方面取得了显著的进展,在水文地质勘查方面的应用也进一步拓展。这种在地面直接探测地下水中氢核丰度的技术,其基本原理是利用人工产生的磁场激发地下水中的氢核形成宏观磁矩;这一宏观磁矩在地磁场中进行旋进运动,当激发场停止后,氢核自旋产生弛豫现象;再用地面线圈记录宏观磁矩进动产生的电磁信号,即可判断地下水是否存在[6-10]。该电磁信号E(t, q)即为核磁共振信号,一般可用下式来诠释
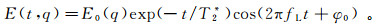 (1)
(1) 其中:t为采样时间;q为激发脉冲矩;E0为与地下水含量成正比的MRS信号初始振幅;T2*为含水层介质平均孔隙度的平均弛豫时间;fL为由测量地点地磁场决定的拉莫尔频率;φ0为与含水层导电性相关的初始相位。E0、T2*、fL、φ0即为MRS信号的四个关键参数。MRS信号关键参数能否被准确提取依赖于测量地点的电磁噪声水平[11]。当信噪比较低时,MRS信号完全淹没在电磁噪声中,难以获得四个关键参数。尽管核磁共振地下水探测方法具有多种优势,但由于MRS信号极其微弱,对周围环境中的电磁干扰敏感成为其应用的主要瓶颈。
影响信号质量最严重的两类电磁噪声是工频谐波噪声和尖峰脉冲噪声。工频谐波噪声来源于电力线、发电机、变压器、工业及生活用电等,频率固定为50或60 Hz的整数倍,或某一频率的单频干扰,其特点是频率固定,且持续时间长。尖峰脉冲噪声主要由太阳磁暴、雷暴或任何物体突然放电产生,一般持续时间很短,干扰幅度较大,高出信号幅度数倍,干扰频率范围较宽。
核磁共振信号的噪声压制近几年成为非常重要的研究热点。早先的核磁共振地下水探测仪采用单一线圈模式[1, 12-15],发射线圈和接收线圈分时复用同一线圈。普遍采用的方法是利用采集数据的多次叠加[11]来提高信噪比。即当噪声强度大时需要叠加的次数多,这将增加测量的时间,导致仪器的工作效率降低。为此,Legchenko等[16]提出采用正弦对消法、区块对消法和陷波滤波法滤除工频谐波干扰;然而,当测量地点的拉莫尔频率与工频谐波的干扰频率较接近时,MRS信号在陷波后会产生严重失真,降低信号的可靠性。在探测方法方面,通过合理铺设“8”字形线圈[17-18]可有效抵消噪声干扰。这种方法在噪声均匀分布的环境中应用效果较好,但其激发场的分布会随着线圈形状的改变而发生变化,影响激发效果。此外,铺设“8”字形线圈探测时探测深度将减小为原来的一半,需要增加线圈尺寸才能达到传统方形或圆形线圈的探测水平。由于最新的仪器可以通过铺设多个接收线圈实现信号和噪声的同步采集,因此通过参考消噪方法可明显提高信号的信噪比[19-20]。参考消噪方法需要用一个探测线圈来测量含有噪声的MRS信号,另外一个或者多个参考线圈在远端同时测量不包含信号的噪声数据,其中最关键的一步是获得使参考线圈数据与探测线圈数据相关的传递函数。2006年,Radic[21]首次描述了频域上的滤波算法,提出使用远端垂直铺设的参考线圈采集空间磁场的水平方向分量,以此对探测线圈中的相关噪声进行抵消计算;但由于参考线圈感应空间磁场水平分量与探测线圈磁场垂直分量的相关性较低,给出的应用结果中仍有较高水平的残余噪声。2008年,Walsh[19]研制多通道地面核磁共振找水系统,从多个通道上提取主通道探测信号与其他通道噪声信号构成新的数据序列,基于频域自适应消噪算法实现噪声滤除。2010年,Muller-Petke等[20]提出了一种基于单参考通道的时域噪声预测滤波器,该滤波器可以自动计算参考通道数据与主通道数据的振幅与相位差,得到含有校正系数的传递函数,实验结果显示该方法可以完整地保留MRS信号,也能对以工频谐波为主的电磁干扰进行压制;然而,通过该方法滤波后的信噪比还有待提升。2012年,Dalgaard等[22]采用时域自适应滤波器实现参考消噪方法,同时发现类似于尖峰脉冲的噪声干扰影响了通道间的数据相关性,需要先剔除尖峰脉冲干扰。2014年,Muller-Petke等[23]开展了时域参考消噪方法和频域参考消噪方法的系统研究,认为频域参考消噪方法的滤波效果优于时域参考消噪方法。另外,法国推出的NUMISPoly系统也是针对存在强电磁干扰的探测环境,采集多个远端的参考数据,抵消信号中的环境噪声;德国推出的NMR-MIDI还加入了远端垂直方向的参考线圈,进一步消除环境噪声影响;我国研究人员采用宽频带滤波器,通过自适应参考消噪技术,在相同的电磁噪声环境下,利用较少的叠加次数获取了较高信噪比的地下水MRS信号[24]。
此外,通过分析噪声特性,采用建模法去除特定的电磁干扰开辟了磁共振噪声压制方法的新领域。2013年,为解决多源噪声干扰下自适应噪声对消方法去噪能力有限的难题,Larsen等[25]提出建模法去除工频谐波噪声,该方法与正弦对消法相似,通过建模构建通带内的工频谐波干扰以提高信噪比。2015年,Larsen[26]使用两个级联的二阶带通滤波器对尖峰脉冲噪声建模,以剔除来源于电网的尖峰脉冲干扰。
吉林大学地下水磁共振探测技术课题组总结国内外研究现状,深入分析噪声的产生机理,针对影响MRS信号质量最严重的两类电磁干扰工频谐波噪声和尖峰脉冲噪声,取得了一系列的噪声压制研究进展。
1 工频谐波噪声压制方法研究进展 1.1 实时参考消噪技术使用吉林大学自主研制的核磁共振多通道宽频带接收系统[27],结合后续数据处理可压制工频谐波噪声;然而,通带内噪声干扰严重容易淹没微弱的MRS信号,导致放大器饱和。针对多通道宽频带接收系统受强电磁干扰放大器易饱和的问题,吉林大学地下水磁共振技术课题组正在开发基于现场可编程门阵列(field-programmable gate array, FPGA)的实时参考消噪技术,将后续的自适应消噪处理环节移植到前端的FPGA中,通过铺设参考线圈采集探测点附近的环境噪声,在信号和噪声未知的情况下,采用变步长最小均方(least mean square, LMS)算法自适应跟踪学习去除相关噪声,在系统不饱和的前提下尽可能提高信噪比,同时可现场实时检测MRS信号。
由于定步长LMS算法的收敛速度与稳态误差相互矛盾,并且对输入信号信噪比要求严格;因此,课题组决定采用变步长LMS算法[28-34]实现实时参考消噪,其本质是利用误差因子的e指数形式作为步长参数,进行自适应滤波。变步长表达式为
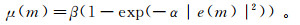 (2)
(2) 式中:m是离散的采样时间;μ是控制算法稳定性和收敛性的步长因子;e是误差信号;α是控制函数形状的常数;β是控制函数取值范围的常数。
理想的步长参数是:当e(m)较大时,选择较大的步长因子加快收敛速度;当e(m)较小时,选择较小的步长因子减小稳态误差。该e指数变步长表达式初始时刻e(m)较大,步长大小主要取决于参数β,而达到稳态时e(m)很小,步长趋于0;符合理想步长参数要求。通过适当调整参数β,可使算法快速稳定收敛。含有指数因子的变步长LMS算法不仅可以快速稳定地收敛,而且具有较好的鲁棒性;同时对输入信号的信噪比要求降低,是实现实时参考消噪算法较好的选择。
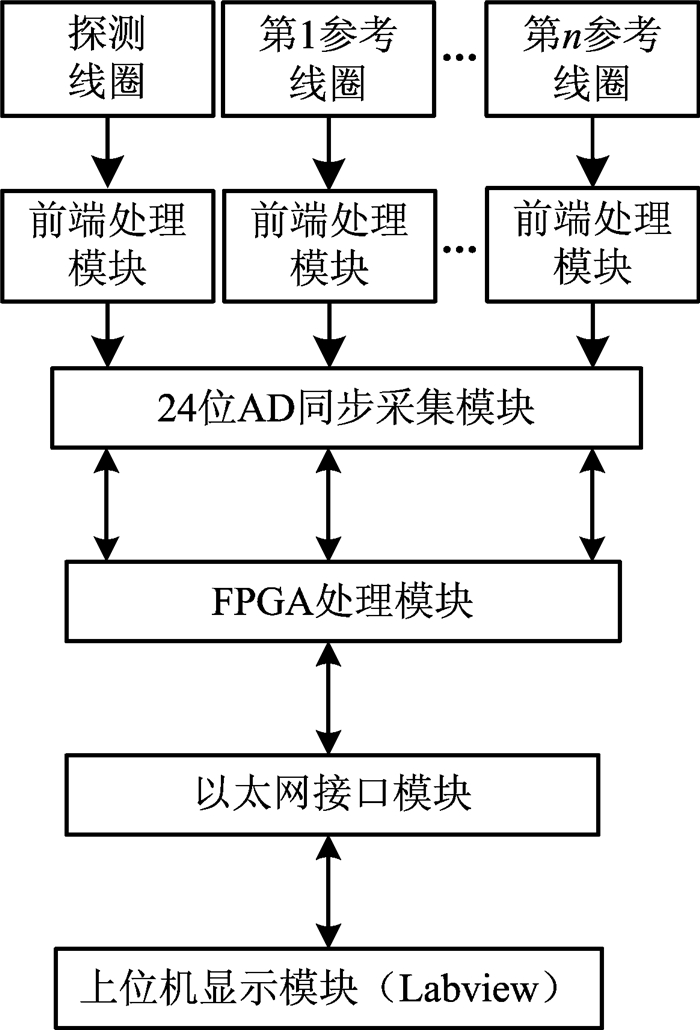
在核磁共振宽频阵列式接收系统[27]中嵌入变步长LMS滤波模块,以实现实时参考消噪,其原理如图 1所示。前端处理模块由低噪声前放和宽频带带通滤波器构成,实现对信号的前置放大和初步滤波;使用24位超低噪声模数转换器(analog to digital converter, A/D)采集模块对信号进行同步采集并送至FPGA,在FPGA中利用变步长LMS滤波器对含有工频谐波噪声的核磁信号进行处理;最后通过以太网接口模块对处理完的数据进行打包送至上位机,并在Labview中实时显示。
|
| 图 1 多通道实时自适应参考消噪原理 Figure 1 Multichannel adaptive noise cancelling in real time |
|
|
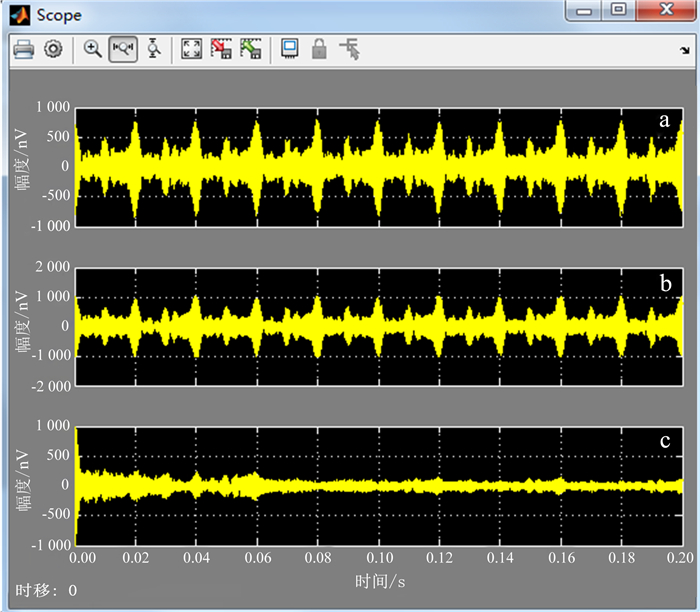
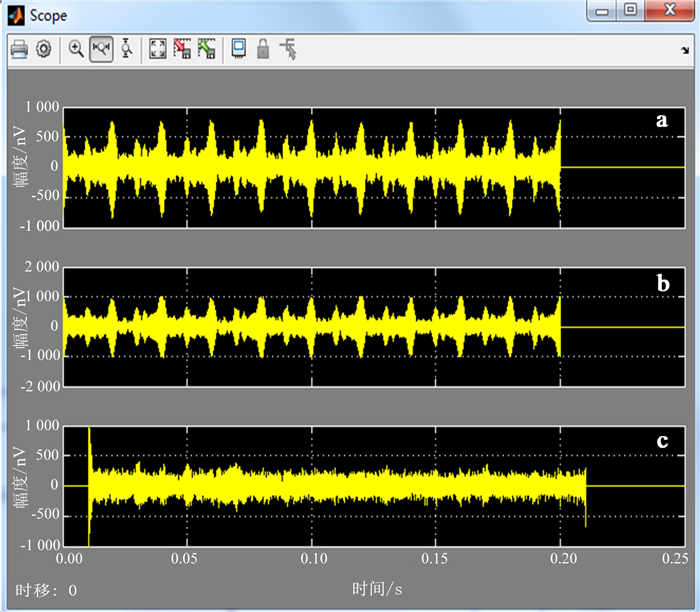
图 2和图 3分别为30阶变步长LMS滤波器理论模型仿真和硬件实时测试结果。测试结果表明,主通道中被工频噪声淹没的核磁信号自适应滤波后获得了自由衰减的MRS信号。由于FPGA的电路效应,滤波器输出会产生短暂延时,输出不能立即随输入变化,出现竞争冒险,产生高频毛刺信号;可通过在FPGA的输出端并联小电容去除该毛刺信号。此外,硬件实时测试结果表明,当参考通道信号和主通道信号在0.20 s后为0时,消噪后的信号经电路延时后也为0;再次证明变步长LMS滤波算法在FPGA中是实时实现的。对基于理论模型的软件仿真结果和基于FPGA的硬件实测结果进行频谱分析,硬件实测结果虽然没有理论仿真效果好;但总体而言,在FPGA中运行变步长LMS算法可以很大程度地实时抑制磁共振信号中的工频谐波干扰,有效防止系统饱和,最大限度地从环境噪声中提取有用的核磁共振信号,且不发生畸变和衰减。
|
| a.参考通道信号;b.主通道信号;c.消噪后的信号。 图 2 30阶变步长LMS滤波器理论模型仿真 Figure 2 Theoretical model simulation of thirty-order LMS filter with variable-step |
|
|
|
| a.参考通道信号;b.主通道信号;c.消噪后的信号。 图 3 30阶变步长LMS滤波器硬件实时测试结果 Figure 3 Hardware test result of thirty-order LMS filter with variable-step in real time |
|
|
陷波法[16]和参考消噪方法[19-20]均是基于信号和噪声在时频域上具有不同特征加以分离;然而,噪声的无规律性、不稳定性以及混合机理的不确定性限制了算法的有效应用。独立分量分析(independent component analysis, ICA)方法[35-40]作为一种有效的盲源分离手段,其基本思路是,在源信号、噪声以及混合机理均未知的情况下,假设一组相互独立的源信号经过线性混合系统后得到一组混合信号,通过选择某种独立性判据,构造一个多通道混合信号的目标函数,再利用合适的优化算法调节解混矩阵以得到最优解,最终得到各分量之间相互独立的输出信号,以分离源信号。主要包括四个步骤。
1)首先对观测信号进行去均值处理,使数据中心化:
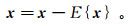 (3)
(3) 式中:x是观测信号;E{·}是求观测信号的均值。
2)对零均值信号进行白化处理,得到数据z(t)。该数据具有单位方差,数据之间的相关性较低。白化处理的表达式为
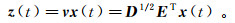 (4)
(4) 式中,D和E分别是观测信号的协方差矩阵特征值和特征向量。
3)利用基于负熵最大化原理和牛顿迭代求解解混矩阵w,得到独立成分y:
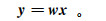 (5)
(5) 4)数据重构,保留MRS信号的独立分量,屏蔽噪声分量,恢复信号幅度:
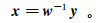 (6)
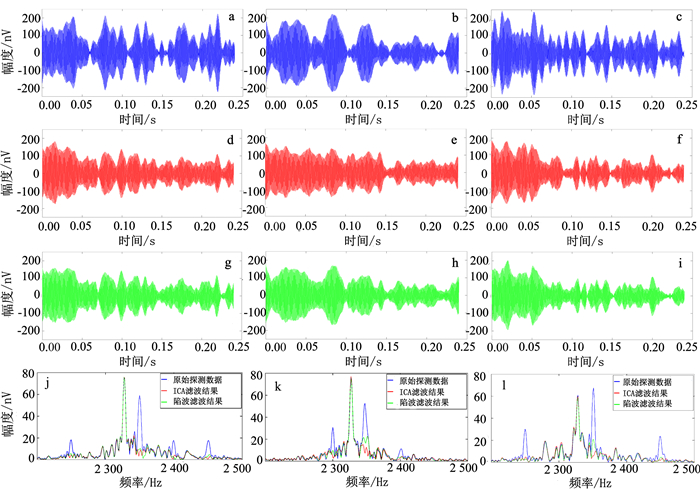
(6) 吉林大学地下水磁共振探测技术课题组利用自主研制的磁共振地下水探测仪[9, 41]在长春市烧锅镇开展了基于独立分量分析技术抑制工频谐波噪声的试验研究。采用边长为100 m的方形单匝线圈,激发频率为2 326 Hz,得到相同激发脉冲矩下三个含噪声磁共振信号的时域波形图(图 4ac);采用基于独立分量分析技术抑制工频谐波噪声后的信号如图 4df所示。为了验证算法的有效性,将独立分量分析方法与陷波法进行比较。图 4gi是陷波法去除工频谐波噪声后信号的时域波形,图 4jl是消噪前后信号的频域对比结果。经对比分析得到结论:独立分量分析技术对工频谐波噪声的抑制效果优于陷波法。
|
| ac.随机选取的三组同一脉冲矩激发下含噪声的磁共振信号;df.使用ICA方法分别抑制ac中的工频谐波噪声后的信号;gi.使用陷波法分别去除ac中工频谐波噪声后的信号;jl. ICA方法和陷波法滤波前后的频域对比结果。 图 4 抑制工频谐波噪声实例 Figure 4 Examples of power-line harmonic cancelling |
|
|
通常的磁共振信号尖峰噪声处理方法是基于统计原理找到数据中的“粗大误差”,然后进行删除或修正,正如广泛应用的统计叠加方法[42]。然而,针对干扰幅度较小的尖峰噪声,统计叠加法很难剔除。因此,利用基于能量运算的尖峰噪声抑制技术,通过计算信号的能量,可有效检测尖峰噪声并突出不易识别的小幅度尖峰噪声。主要包括三个步骤。
1)计算单次采集信号的能量,将信号由时域转化到能量域;再将计算后信号的能量通过低通滤波器。设xn为采样信号,其能量En可表示为
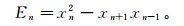 (7)
(7) 2)经过上述能量运算后,尖峰噪声被突出,此时需要选取适当的阈值进行尖峰识别并剔除。基于中位数的绝对偏差(median absolute deviation, MAD)法[43]是一种非常有效的统计学方法,定义为
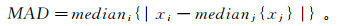 (8)
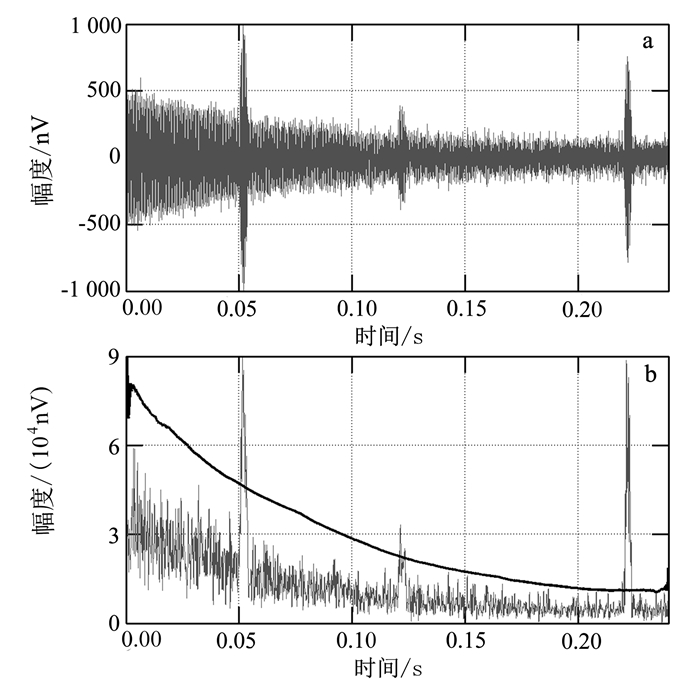
(8) 式中:xi为该时刻某次采集的数据点,xj为某一时刻所有单次采集的数据列;medianj{·}是求该数据列的中位数。计算MAD后,阈值为median{x}+k·MAD(K是常数)。根据尖峰噪声和信号在能量域中的幅值关系,阈值以能有效标记出被突出信号的能量为标准进行选取。如图 5所示,尖峰噪声在能量域中被突出,使用基于中位数的绝对偏差法确定的阈值既跟踪了信号的整体变化趋势,又有效地将幅度较小的尖峰噪声标记出。
|
| a.受尖峰噪声干扰的MRS信号;b.信号能量及阈值。 图 5 基于中位数绝对偏差法确定阈值的峰值检测实例 Figure 5 Example of spike detection based on threshold determined by MAD method |
|
|
3)将能量域中的信号与阈值进行比较,超出阈值的部分视作尖峰噪声,用该时刻无尖峰噪声数据列的中位数进行替代,以达到剔除尖峰噪声的目的。
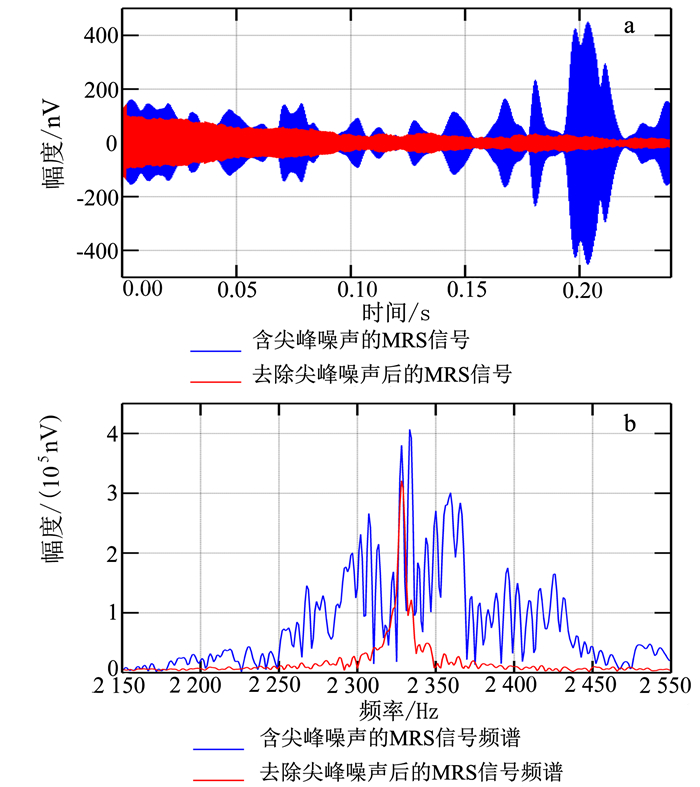
为了验证算法的实用性,在长春市郊区烧锅镇进行了野外实验。使用核磁共振地下水探测仪[9]进行信号采集。当地的拉莫尔频率为2 326 Hz,图 6a中的蓝色线为仪器采集的原始信号时域波形图。从图 6a中可以看出:该信号含有较多的尖峰噪声,并且从信号的时域波形上不能明显看出MRS信号指数型的衰减趋势。经计算,原始信号的信噪比为-37.709 0 dB。
|
| a.剔除尖峰噪声前后的时域图;b.剔除尖峰噪声前后的频域图。 图 6 基于能量运算的尖峰噪声抑制方法剔除实测数据中的尖峰噪声 Figure 6 Spikes in MRS experimental data removed by energy calculation approach |
|
|
依次操作能量运算法的三个步骤,对图 6a所示的实测数据进行尖峰噪声剔除,得到消噪后的时域信号,如图 6a中的红色线所示。可见,原始信号中的尖峰噪声被明显剔除,消噪后的信号呈现指数形式衰减。再从频域上进行比较,结果是消噪后尖峰噪声的频率分量被压制,突出了信号的频率,如图 6b所示。经计算,消噪后信号的信噪比为-29.138 0 dB,剔除尖峰噪声后信噪比提高了8.571 0 dB。
2.2 基于同步压缩小波变换和自寻优非线性阈值的补偿技术基于统计学原理识别尖峰噪声,进行数据替代时很容易损失MRS信号的有效信息,可采用基于同步压缩小波变换[44-46]和自寻优非线性阈值补偿技术[47]抑制尖峰噪声的方法同时重构MRS信号,提高信噪比。
实现同步压缩小波变换,首先要设定所要采用的小波母函数和所要划分的压缩小波域的长度,对所划分不同压缩小波域内的磁共振信号求解压缩小波系数。同步压缩小波变换表达式为
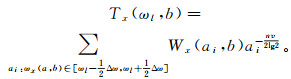 (9)
(9) 式中:Tx(ωl, b)为同步压缩小波系数;Wx(ai, b)为连续小波变换的小波系数;ai为尺度因子a的离散值;b为平移因子;ωl为中心频率,在一个连续区间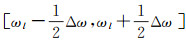
对同步压缩小波变换后信号用自寻优算法搜寻尖峰噪声在信号中的位置,并将其剔除。自寻优算法表示为
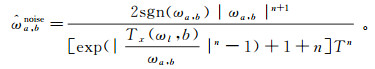 (10)
(10) 式中: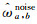
运用非线性阈值选取算法对尖峰噪声所在位置的MRS信号进行补偿,确定所需非线性阈值函数:j, k=sign(ωj, k)×[(ωj, k-k)·(ωj, k)2+λ2/(2λ+k)k],
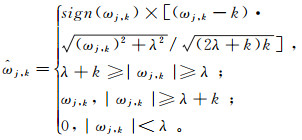 (11)
(11) 式中:ωj, k为原始数据的压缩小波系数;j, k为去除尖峰噪声后获得的新的压缩小波系数;λ为预先设定的阈值;σ为可调参数。
最后,对经过自寻优算法以及非线性阈值选取算法处理后的MRS信号进行压缩小波重构,得到最终的剔除尖峰噪声后的MRS信号。
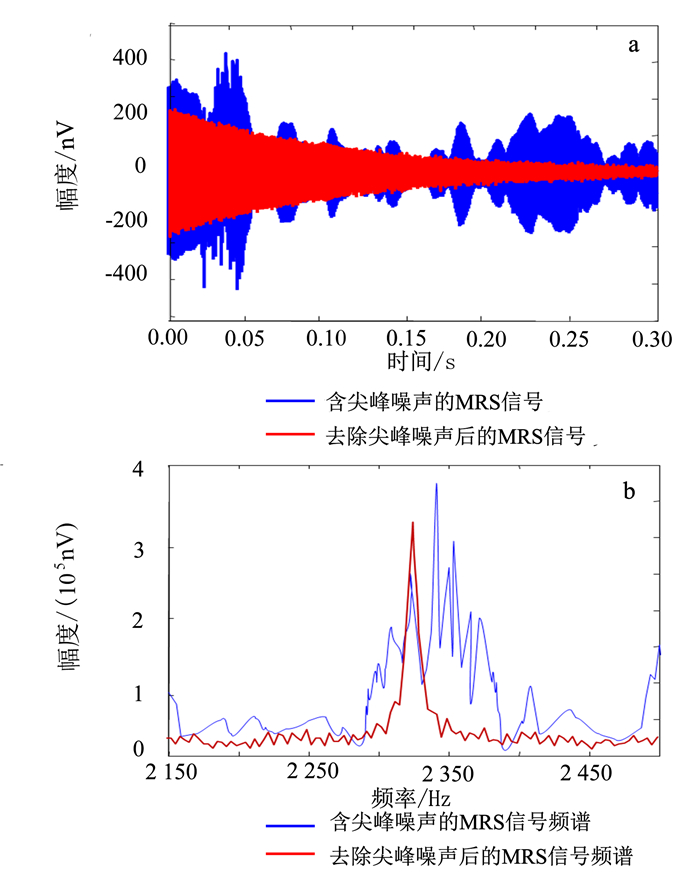
为了证明算法的有效性,在长春市净月潭进行试验。使用核磁共振地下水探测仪[9]进行信号采集。当地的拉莫尔频率2 330 Hz,图 7为应用基于同步压缩小波变换和自寻优非线性阈值补偿技术后重构的MRS信号。
|
| a.剔除尖峰噪声前后的时域图;b.剔除尖峰噪声前后的频域图。 图 7 基于同步压缩小波变换和自寻优非线性阈值补偿方法剔除实测数据中的尖峰噪声 Figure 7 Spikes in MRS experimental data removed by synchronous pressure wavelet and self-optimizing nonlinear threshold compensation |
|
|
伴随多通道磁共振探测系统的引入,使用宽频带数据采集,为进一步提高信噪比提供了更多的潜能,目前已经在地下水磁共振信号的工频谐波噪声和尖峰脉冲噪声压制方面取得了有效的研究成果和进展。然而,较宽的通频带会引入更多的随机噪声,若采用传统的叠加方法,需要增加叠加次数,且滤波效果有限,严重降低探测效率。因此,亟需研究核磁共振信号随机噪声的压制方法。
由于随机噪声在时间域中会淹没微弱的核磁共振信号,影响核磁共振信号的检测与提取,在频率域中,其功率谱分布在整个通频带范围内,与有效信号的功率谱重叠,难以在时间域或频率域内有效压制随机噪声;因此,如何把含随机噪声的信号投影到某一特定空间,进而有效区分信号和噪声,利用信号和噪声的不同特性压制随机噪声,将是磁共振地下水探测噪声压制方法未来具有挑战性的发展方向。
| [1] | Legchenko A V, Baltassat J M, Beauce A, et al. Nuclear Magnetic Resonance as a Geophysical Tool for Hydrogeologists[J]. Journal of Applied Geophysics , 2002, 50 (1/2) : 21-46. |
| [2] | Lehmann-Horn J A, Hertrich M, Greenhalgh S A, et al. Three-Dimensional Magnetic Field and NMR Sensitivity Computations Incorporating Conductivity Anomalies and Variable-Surface Topography[J]. IEEE Transactions on Geoscience and Remote Sensing , 2011, 49 : 3878-3891. DOI:10.1109/TGRS.2011.2135861 |
| [3] | Hertrich M, Green A G, Braun M, et al. High-Resolution Surface-NMR Tomography of Shallow Aquifers Based on Multi-Offset Measurements[J]. Geophysics , 2009, 74 (6) : 47-59. |
| [4] | Mueller-Petke M, Yaramanci U. QT Inversion: Comprehensive Use of the Complete Surface NMR Data Set[J]. Geophysics , 2010, 75 (4) : 199-209. DOI:10.1190/1.3471523 |
| [5] | Gunther T, Muller-Petke M. Hydraulic Properties at the North Sea Island of Borkum Derived from Joint Inversion of Magnetic Resonance and Electrical Resistivity Soundings[J]. Hydrology and Earth System Sciences , 2012, 16 : 3279-3291. DOI:10.5194/hess-16-3279-2012 |
| [6] | Legchenko A V, Valla P. A Review of the Basic Principles for Proton Magnetic Resonance Sounding Measurements[J]. Journal of Applied Geophysics , 2002, 50 (1/2) : 3-19. |
| [7] | Lubczynski M, Roy J. Hydrogeological Interpretation and Potential of the New Magnetic Resonance Sounding (MRS) Method[J]. Journal of Hydrology , 2003, 283 (1/2/3/4) : 19-40. |
| [8] | Roy J, Lubczynski M. The Magnetic Resonance So-unding Technique and Its Use for Groundwater Investigations[J]. Hydrogeol J , 2003, 11 (4) : 455-465. DOI:10.1007/s10040-003-0254-8 |
| [9] | 林君, 段清明, 王应吉, 等. 核磁共振找水仪原理与应用 [M]. 北京: 科学出版社, 2010 . Lin Jun, Duan Qingming, Wang Yingji, et al. Theory and Design of Magnetic Resonance Sounding Instrument for Groundwater Detection and Its Applications [M]. Beijing: Science Press, 2010 . |
| [10] | 潘玉玲, 张昌达. 地面核磁共振找水理论和方法 [M]. 武汉: 中国地质大学出版社, 2000 : 40 . Pan Yuling, Zhang Changda. The Theory and Methods of Water Detecting [M]. Wuhan: China University of Geosciences Press, 2000 : 40 . |
| [11] | 蒋川东.核磁共振地下水探测系统数据处理软件的设计与应用[D].长春:吉林大学, 2009. Jiang Chuandong. Design and Application of Data Processing Software in Magnetic Resonance Sounding System for Groundwater Detection[D]. Changchun: Jilin University, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10183-2009094496.htm |
| [12] | 李振宇, 潘玉玲, 张兵, 等. 利用和磁共振方法研究水文地质问题及应用实例[J]. 水文地质工程地质 , 2003, 30 (4) : 50-54. Li Zhenyu, Pan Yuling, Zhang Bing, et al. Using NMR Method Research the Hydrogeology Problems and Practical Examples[J]. Hydrogeology and Engineering Geology , 2003, 30 (4) : 50-54. |
| [13] | 张小华, 林君, 王应吉, 等. 地面核磁共振(NMR)找水仪发射机的研制[J]. 仪器仪表学报 , 2006, 27 (7) : 689-692. Zhang Xiaohua, Lin Jun, Wang Yingji, et al. Development of the Transmitter in a Surface NMR Water Investigation Instrument[J]. Chinese Journal of Scientific Instrument , 2006, 27 (7) : 689-692. |
| [14] | 王中兴.地面核磁共振找水仪关键技术的研究[D].长春:吉林大学, 2009. Wang Zhongxing. The Key Technology of Magnetic Resonance Sounding Instrument for Groundwater Investigation[D]. Changchun: Jilin University, 2009. http://www.cnki.com.cn/Article/CJFDTOTAL-CCYD200703006.htm |
| [15] | 荣亮亮.多匝线圈核磁共振找水技术研究[D].长春:吉林大学, 2009. Rong Liangliang. Study on Multi-Turn Loop Magnetic Resonance Sounding (MRS) Technique for Underground Water[D]. Changchun: Jilin University, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10183-1012366719.htm |
| [16] | Legchenko A, Valla P. Removal of Power-Line Harmonics from Proton Magnetic Resonance Sounding Measurements[J]. Journal of Applied Geophysics , 2003, 53 : 103-120. DOI:10.1016/S0926-9851(03)00041-7 |
| [17] | |
| [18] | Lange G, Meyer R, Battista M D, et al. Loop Configuration Experiments on Multiple Layered Primary Aquifers in South Africa and Germany[C]// 3rd Magnetic Resonance Sounding Workshop. Madrid: Autonomous University, 2006. |
| [19] | Walsh D O. Multi-Channel Surface NMR Instrumentation and Software for 1D/2D Groundwater Investigations[J]. Journal of Applied Geophysics , 2008, 66 (3/4) : 140-150. |
| [20] | Muller-Petke M, Yaramanci U. Improving the Signal-to-Noise Ratio of Surface-NMR Measurements by Reference Channel Based Noise Cancellation[C]// 16th European Meeting of Environmental and Engineering Geophysics. Zurich: EAGE, 2010. |
| [21] | Radic T. Improving the Signal-to-Noise Ratio of Surface NMR Data Due to the Remote Reference Technique[C]//12th European Meeting of Environmental and Engineering Geophysics. Helsinki: EAGE, 2006. |
| [22] | Dalgaard E, Auken E, Larsen J. Adaptive Noise Cancelling of Multichannel Magnetic Resonance Sounding Signals[J]. Geophysical Journal International , 2012, 191 (1) : 88-100. DOI:10.1111/gji.2012.191.issue-1 |
| [23] | Muller-Petke M, Costabel S. Comparison and Optimal Parameter Setting of Reference-Based Harmonic Noise Cancellation in Time and Frequency Domain for Surface-NMR[J]. Near Surface Geophysics , 2014, 12 : 199-210. |
| [24] | 林君, 蒋川东, 段清明, 等. 复杂条件下地下水磁共振探测与灾害水源探查研究进展[J]. 吉林大学学报(地球科学版) , 2012, 42 (5) : 1560-1570. Lin Jun, Jiang Chuandong, Duan Qingming, et al. The Situation and Progress of Magnetic Resonance Sounding for Groundwater Inverstigations and Underground Applications[J]. Journal of Jilin University (Earth Science Edition) , 2012, 42 (5) : 1560-1570. |
| [25] | Larsen J J, Dalgaard E, Auken E. Noise Cancelling of MRS Signals Combining Model-Based Removal of Powerline Harmonics and Multichannel Wiener Filtering[J]. Geophysical Journal International , 2014, 196 : 828-836. DOI:10.1093/gji/ggt422 |
| [26] | Larsen J J. Model-Based Subtraction of Spikes from Surface-NMR Data[C]// 6th Magnetic Resonance Sounding International Workshop. Arhus: [s. n.], 2015. |
| [27] | 曲永星.阵列式宽带核磁共振全波采集系统的研制[D].长春:吉林大学, 2015. Qu Yongxing. Development of Broadband Array Full Wave MRS Acquisition System[D]. Changchun: Jilin University, 2015. |
| [28] | 田宝凤, 段清明. 核磁共振信号工频谐波的自适应滤除方法[J]. 吉林大学学报(信息科学版) , 2009, 27 (3) : 223-228. Tian Baofeng, Duan Qingming. Removal Method of Industrial Frequency Harmonics in Nuclear Magnetic Resonance Signal Based on Adaptive Filter[J]. Journal of Jilin University (Information Science Edition) , 2009, 27 (3) : 223-228. |
| [29] | 田宝凤, 林君, 段清明, 等. 基于参考线圈和变步长自适应的磁共振信号噪声压制方法[J]. 地球物理学报 , 2012, 55 (7) : 2462-2472. Tian Baofeng, Linjun, Duan Qingming, et al. Variable Step Adaptive Noise Cancellation Algorithm for Magnetic Resonance Sounding Signal with a Reference Coil[J]. Chinese Journal of Geophysics , 2012, 55 (7) : 2462-2472. |
| [30] | Farhang-Boroujeny B. Adaptive Filters: Theory and Applications [M]. New York: John Wiley & Sons Inc, 1998 . |
| [31] | 郝荟萃.基于自适应参考消噪的磁共振全波信号处理方法研究[D].长春:吉林大学, 2013. Hao Huicui. Processing Method of Full Wave Magnetic Resonance Sounding Signal Based on Adaptive Reference Cancellation[D]. Changchun: Jilin University, 2013. |
| [32] | Widrow B, Glover J R, McCool J M, et al. Adaptive Noise Cancelling: Principles and Applications[J]. Proceedings of the IEEE , 1975, 63 (12) : 1692-1716. DOI:10.1109/PROC.1975.10036 |
| [33] | 高晋占. 微弱信号检测 [M]. 北京: 清华大学出版社, 2004 . Gao Jinzhan. Weak Signal Detection [M]. Beijing: Tsinghua University Press, 2004 . |
| [34] | 何振亚. 自适应信号处理 [M]. 北京: 科学出版社, 2004 . He Zhenya. Adaptive Signal Processing [M]. Beijing: Science Press, 2004 . |
| [35] | An Y W, Wang S. Study on Application of Independent Component Analysis in the CSNS/RCS[J]. Chinese Acta Physica Sinica , 2013, 37 : 037006. |
| [36] | 王文波, 张晓东, 汪祥莉. 基于独立成分分析和经验模态分解的混沌信号降噪[J]. 物理学报 , 2013, 62 (5) : 050201. Wang Wenbo, Zhang Xiaodong, Wang Xiangli. Chaotic Signal Denoising Method Based on Independent Component Analysis and Empirical Mode Decomposition[J]. Chinese Acta Physica Sinica , 2013, 62 (5) : 050201. |
| [37] | Comon P. Independent Component Analysis, A New Concept?[J]. Signal Processing , 1994, 36 (3) : 287-314. DOI:10.1016/0165-1684(94)90029-9 |
| [38] | Hyvarinen A. Fast and Robust Fixed-Point Algorithms for Independent Component Analysis[J]. IEEE Transactions on Neural Networks , 1999, 10 (3) : 626-634. DOI:10.1109/72.761722 |
| [39] | Hyvarinen A, Oja E. A Fast Fixed-Point Algorithm for Independent Component Analysis[J]. Neural Computation , 1997, 9 (7) : 1483-1492. DOI:10.1162/neco.1997.9.7.1483 |
| [40] | 付卫红, 杨小牛, 刘乃安. 基于四阶累积量的稳健的通信信号盲分离算法[J]. 电子与信息学报 , 2008, 30 (8) : 1853-1856. Fu Weihong, Yang Xiaoniu, Liu Naian. Robust Algorithm for Communication Signal Blind Separation Fourth Order Cumulant-Based[J]. Journal of Electronics and Information Technology , 2008, 30 (8) : 1853-1856. |
| [41] | 史文龙.核磁共振地下水探测全波接收系统原理样机研制[D].长春:吉林大学, 2014. Shi Wenlong. Full-Wave Receiver of MRS Groundwater Exploration System[D]. Changchun: Jilin University, 2014. |
| [42] | Jiang C D, Lin J, Duan Q M, et al. Statistical Stacking and Adaptive Notch Filter to Remove High-Level Electromagnetic Noise from MRS Measurements[J]. Near Surface Geophysics , 2011, 9 (5) : 459-468. |
| [43] | Hoaglin D C, Mosteller F, Tukey J W. Understanding Robust and Exploratory Data Analysis [M]. Wiley Classics Library Press, 2000 . |
| [44] | Chavez-Roman H, Ponomaryov V. Super Resolution Image Generation Using Wavelet Domain Interpolation with Edge Extraction via a Sparse Representation[J]. IEEE Geoscience Remote Sensing Letters , 2014, 11 (10) : 1777-1781. DOI:10.1109/LGRS.2014.2308905 |
| [45] | Iqbal M, Chafoor A, Siddiqui A. Satellite Image Resolution Enhancement Using Dual-Tree Complex Wavelet Transform and Nonlocal Means[J]. IEEE Geoscience Remote Sensing Letters , 2013, 10 (3) : 451-455. DOI:10.1109/LGRS.2012.2208616 |
| [46] | Parrilli S, Poderico M, Angelino C, et al. A Nonlocal SAR Image Denoising Algorithm Based on LLMMSE Wavelet Shrinkage[J]. IEEE Transactions on Geoscience and Remote Sensing , 2012, 50 (2) : 606-616. DOI:10.1109/TGRS.2011.2161586 |
| [47] | Demirel H, Anbarjafari G. Discrete Wavelet Transform-Based Satellite Image Resolution Enhancement[J]. IEEE Transactions on Geoscience and Remote Sensing , 2011, 49 (6) : 1997-2004. DOI:10.1109/TGRS.2010.2100401 |


