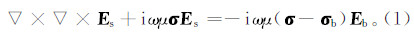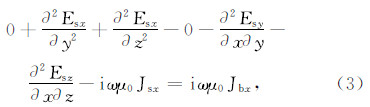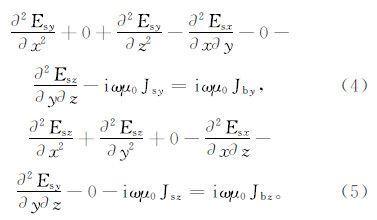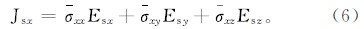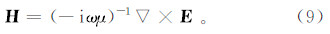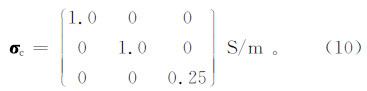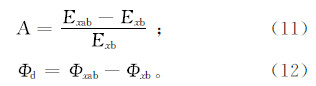2. 辽宁省水利水电勘测设计研究院, 沈阳 110006
2. Investigation and Design Institute of Water Resources and Hydropower Liaoning Province, Shenyang 110006, China
0 引言
近年来，海洋可控源电磁法(marine controlled-source electromagnetics,MCSEM)作为一种钻前储层评估的有效方法，在海洋油气勘探方面正发挥着越来越重要的作用[1]。早期利用海洋可控源电磁法进行油气勘探都是在水深大于1 km的海域进行，此时空气和海水分界面的空气波对高阻异常体返回的有用信号影响不大。然而当海水较浅时，发射源和接收器均接近海面，受空气波的影响，高阻异常体的信号会被大部分掩盖[2]，MCSEM对高阻油气层的识别能力被减弱。为了克服空气波的影响，学者们开展了大量工作。例如，David Andreis等[3]利用一维解析算法对浅海CSEM的物理特征进行分析，对地层及空气波信号进行耦合，进而提高了数据解释的精度；在浅海海洋大地电磁测量中，Løseth等[4]利用一条拖缆上的多对接收机采集MCSEM电磁数据，并对不同的场分量进行加权得到一种有效压制空气波的方法；Jiuping Chen等[5]给出3种有效压制CSEM空气波的方法并应用到二维模拟中；殷长春等[6]对前人空气波的研究做了系统总结，分析了各种方法的优缺点，提出多种压制手段并提及无空气波测量会有深远的研究意义；Sasaki[7]提出了含空气波直接反演方法等。随着空气波压制方法的不断发展及反演技术的日益提高，目前已能较好地处理与反演浅海区海洋电磁数据。为进一步提高浅海海洋电磁数据的解释水平，参考深海海洋电磁数据的解释经验，需要研究复杂介质中的浅海海洋电磁响应特征。
由于受海洋沉积环境、岩石矿物组成等因素的影响，海底往往呈现出各向异性的特征。对于深海情况，学者们开展了大量关于海底各向异性对海洋可控源电磁响应影响特征的研究，并成功用于指导深海数据反演与解释。例如，Weiss等[8]通过有限差分结果与解析解的比对，验证了利用交错网格有限差分法在三维全各向异性介质中数值模拟的可行性；Kong等[9]利用有限元法进行2.5维垂直各向异性的海洋可控源电磁法正演模拟；Weidelt[10]将三维各向异性算法应用到大地电磁正演中；Li等[11]研究了二维倾斜各向异性的海洋可控源电磁法正演模拟，分析了振幅(MVO)和相位(PVO)曲线以及海底电流的分布情况；Wiik等[12]研究了2.5维水平各向同性介质中的海洋可控源电磁法正演问题，并分析了各向异性对振幅和相位的影响；殷长春等[13]利用有限差分对三维任意各向异性介质中海洋可控源电磁法正演算法进行了系统研究，通过MVO、PVO曲线及海底电流分布分析各向异性对海洋可控源电磁法三维正演的影响。Newman等[14]开发了基于TI (transversal isotropy)模型的三维海洋电磁各向异性反演程序，并成功应用于实际数据的处理中。这些研究结果表明，在海洋电磁数据的处理当中考虑各向异性的影响可以得到更准确的反演和解释结果。
浅水区域的海洋可控源电磁信号受空气波影响很大，其各向异性影响特征较深海有较大不同；因此，开展浅海海洋可控源各向异性介质电磁响应特征研究有很大的必要性。本文在利用高精度三维正演程序计算不同模型海洋电磁响应的基础上，分析浅海情况下各向异性对海洋电磁响应的影响特征并总结其物理成因，为浅海海洋电磁数据解释提供一定参考。
1 基本理论 1.1 正演理论本文的三维频率域海洋可控源电磁正演计算基于如下二次电场偏微分方程：
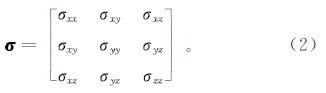
其中：μ为磁导率；σ为模型电导率；ω为角频率；Eb为发射偶极在背景电导率σb中产生的一次背景场；Es为二次电场[15]。σ和σb为对称正定3×3电导率张量，σb设为层状模型或均匀半空间模型。本文利用全空间格林函数计算方法计算背景场Eb[16]。在任意各向异性介质中，电导率张量可表示为
其中，下角标x,y,z表示Cartesian 坐标系中的3个方向。非对角线上的电导率元素将不同方向的电场和电流密度耦合起来。在实际的数值模拟中，一般假定电导率张量σ是由一个参考电导率张量经过三次欧拉旋转得到的[17]。
为求取二次电场Es，将式(1)展开成3个标量方程，即
其中：Jsx、Jsy和Jsz分别为二次电流密度x、y、z方向的分量；Jbx、Jby和Jbz分别为一次电流密度x、y、z方向的分量。利用13 点格式的有限差分技术将计算区域离散成Cartesian坐标下的网格。假设电场分量Esx、Esy和Esz位于剖分网格的棱边上，二次磁场分量Hsx、Hsy和Hsz位于剖分网格面的中心，剖分网格利用角标(i,j,k)标记，如图 1所示。黑色节点之间的电场分量被用来计算各向同性或者三轴各向异性的电流密度，只有计算任意各向异性情况的电流密度时才需要使用白色节点与黑色节点之间的电场分量。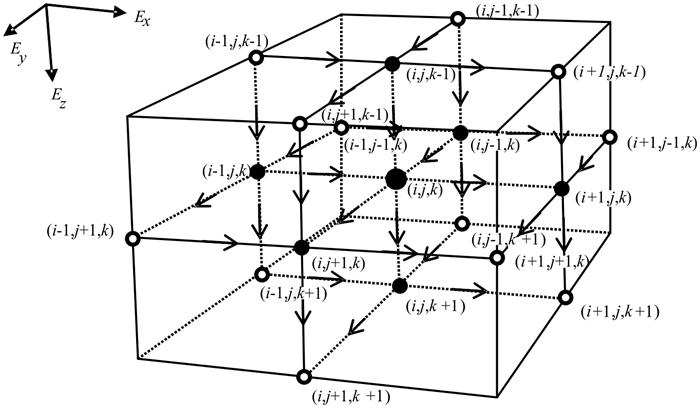
 |
| 图 1 有限差分模拟网格 Fig. 1 Grids for finite-difference modeling |
| |
为离散方程(3)(5)，需要将网格上的电导率近似到电场计算点上并计算其电流密度。在任意各向异性介质中，Jsx的表达式为
当电场分量与所计算的电流密度方向相同时，直接采用体积平均的方式求取平均电导率元素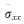
；而方程(6)右端后两项中的平均电导率元素
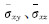则需要用电流密度空间加权平均的方式进行离散[18]。在对方程(3)(5)离散后即可得到形如
根据得到的背景电场Eb和二次电场Es即可得到总的电场：
利用法拉第定律，即可得到磁场的计算公式： 1.2 精度验证
目前，针对海底为各向异性介质的浅海海洋可控源电磁模拟研究较少，只能与深海情况下的海洋可控源各向异性电磁正演结果进行精度验证。本文利用Løseth 2007年发表的一维倾斜各向异性的正演结果[20]进行验证。精度验证模型如图 2a所示。海水深度为300 m，电导率为3.2 S/m；海底围岩电导率为1.0 S/m；高阻层为各向异性介质，参考电导率张量σ=diag(0.01,0.01,0.025) S/m，绕y轴旋转30°，位于海底1 000 m处；发射机为距海底30 m的水平电偶源，长度1 m，发射电流1 A，发射频率0.25 Hz。经过对比(图 2b、c)，本文计算结果与该一维半解析的结果最大相对误差不超过1.7%，具有较高的计算精度。
 |
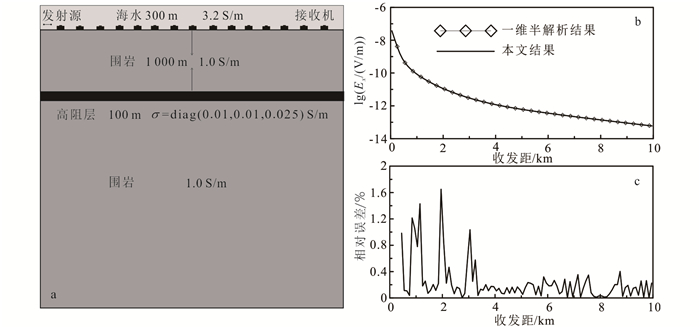| 图 2 精度验证 Fig. 2 Accuracy check of modeling algorithm |
| |
在使用水平电偶极源作为发射源进行MCSEM观测时，接收机主要接收到如图 3所示的4种电磁波，经过高阻体的导波是解译高阻储油层最有效的信号。当进行浅海区观测时，空气波的幅值要远远大于其他电磁信号，尤其是大收发距的区域，接收到的电磁信号中空气波基本会完全掩盖高阻异常体的有用信号。为利用海洋可控源电磁法研究浅海情况下海底各向异性介质的电磁响应特征，本文建立深海和浅海两种情况的三维任意各向异性模型(图 4)。
 |
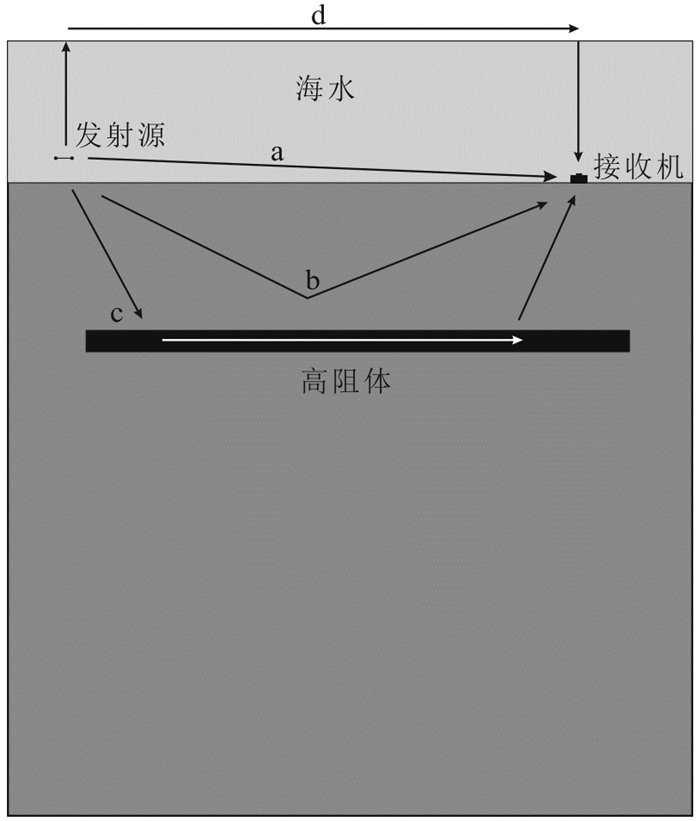| a. 海水中的直达波；b. 海底地层波；c. 高阻体中的导波；d. 空气波。 图 3 MCSEM测量中海底电磁波传播图 Fig. 3 Propagation of marine CSEM waves |
| |
 |
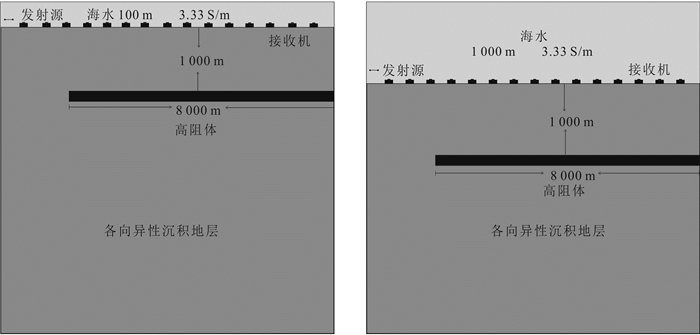| 图 4 海洋可控源电磁法三维地电模型(y=0剖面) Fig. 4 3D model of marine CSEM (y=0) |
| |
假设空气的电导率为无穷小，海水电导率为3.33 S/m，海水深度为100 m、1 000 m两种情况，参考电导率张量为
接收机布设在海底表面，发射机为距海底20 m的水平电偶源，长度1 m，发射电流1 A。设海底最左侧边缘的中心点坐标为(0，0，0)；高阻异常体距离海底1 000 m深，中心点的坐标为(6 000，0，1 000)，大小为8 000 m×4 000 m×100 m，电导率为0.01 S/m。将三维模型剖分成58×58×50个网格单元，每个单元的长、宽、高分别为200 m、200 m、50 m。为得到更精确的高阻异常体响应，将其所在位置的网格进一步细分，z方向的长度为25 m。为更直观地分析海洋可控源电磁法异常大小，定义相对异常A及相位差Φd： 其中，Exab和Φxab，Exb和Φxb分别为含有高阻体模型和背景模型的电场Ex分量的振幅和相位。 2.2 海底各向异性对浅海MCSEM电磁响应的影响 2.2.1 海底背景地层为各向同性及TI介质时的电磁响应特征
为能够分析各向异性海底地层对浅海海洋可控源电磁响应的影响，我们以同线装置(即接收机与发射机所处同一y坐标)为例对MCSEM的MVO和PVO曲线进行分析。
假设海底地层分别为各向同性电导率为σ= 
和参考电导率张量为σc=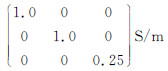 
不旋转两种情况(TI介质)，电磁响应分布如图 5、图 6所示。通过分析，我们可以得到以下几点认识：
 |
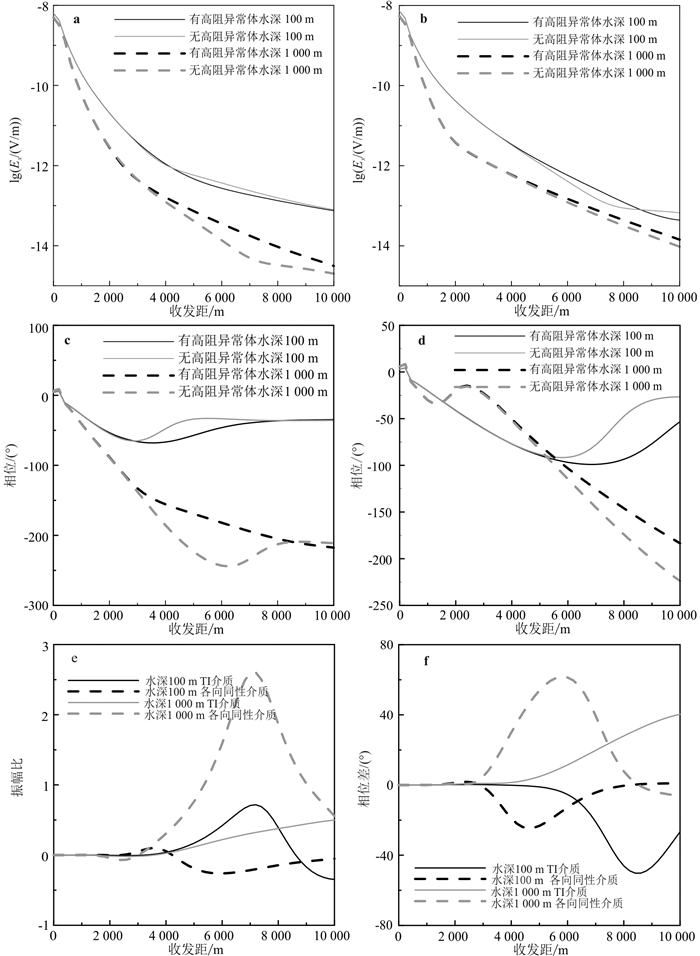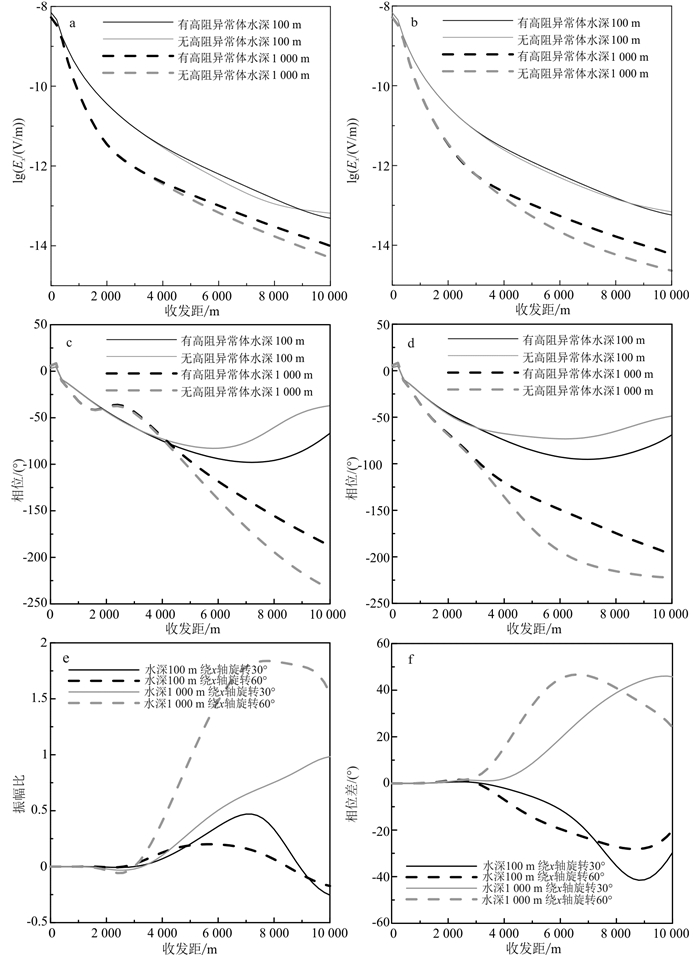
| a.各向同性海底地层的振幅响应；b.TI介质海底地层的振幅响应；c.各向同性海底地层的相位响应；d.TI介质海底地层的相位响应；e.相对振幅异常；f.相位差。 图 5 海底地层为各向同性及TI介质的Ex振幅和相位曲线 Fig. 5 Amplitudes and phases of Ex for the case of isotropic and TI seabed media |
| |
 |
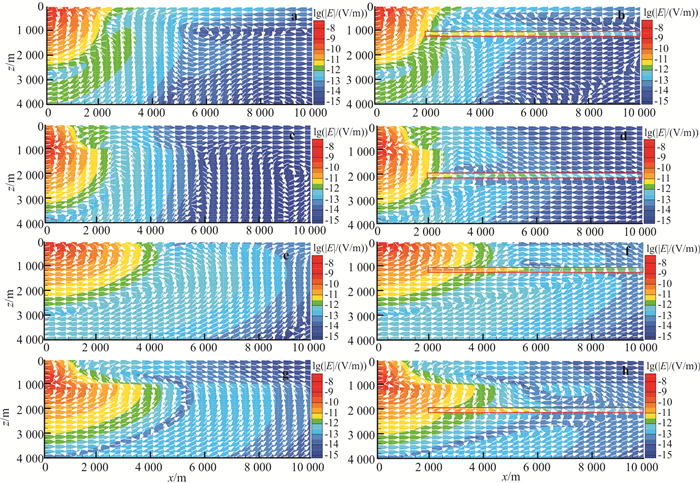| a.水深100 m各向同性介质无异常体；b.水深100 m各向同性介质有异常体；c.水深1 000 m各向同性介质无异常体；d. 水深1 000 m各向同性介质有异常体；e.水深100 m TI介质无异常体；f.水深100 m TI介质有异常体；g.水深1 000 m TI介质无异常体；h.水深1 000 m TI介质有异常体。 图 6 海底地层为各向同性及TI介质的电场及电流分布 Fig. 6 Distribution of E-field and current for anisotropic and TI seabed media |
| |
1)深海和浅海的空气波方向是相反的。空气波的方向主要取决于发射源上方海水中有限范围内的电流方向。对于浅海情况，由于海水较浅，发射源上方海水中的电流少部分从由正极反向流入负极，而大部分在海水中正向传播后经由海底地层流入负极；因此，在发射源上方有限范围内总的电流方向为正向，进而得到正向的空气波。对于深海情况，发射源上方海水中的电流大部分直接由正极流入负极，总的电流方向为负向；因此空气波为反方向。
2)在各向同性介质的大收发距处，浅海中的空气波占主导地位，并被高阻层中的导波抵消一部分，造成幅值下降；而深海中的高阻层中的导波占主导地位，并与空气波相互叠加，造成幅值增大。
3)有、无高阻异常体两种模型响应的振幅和相位曲线存在交点。在浅海情况下：高阻层中的导波与空气波和海底地层波的混合波相互作用造成幅值先增后减，导致两条有、无高阻异常体的曲线出现交点；在TI介质中海底地层波增强，高阻层中的导波随之增强，导致这种交点体现的更明显。在深海情况下，在小收发距时导波与海底地层波相比较弱，对其抵消作用较弱，导致深海情况下虽然有、无高阻异常两种模型的响应曲线也存在交点，但是不如浅海的明显。
4)海底介质从各向同性变为TI介质时，由于海底地层中电磁波衰减较各向同性情况下缓慢，各向同性情况下的电流分布在TI介质中被横向拉伸(各向同性情况下0~4 000 m内的电流分布被拉伸为TI介质情况下0~10 000 m的电流分布)。相应地，振幅与相位曲线均有类似变化。
5)当海底介质由各向同性变为TI介质时，海底地层波衰减变慢。对于浅海情况，海底附近海底地层波与空气波相互抵消造成背景模型响应在5 000~9 000 m范围内减弱；而高阻层中的导波并没有明显减弱，所以相对异常增大。对于深海情况，空气波较弱，对相对异常大小影响不明显，而海底地层波的增强使得相对异常变小。
通过上述分析，浅海情况下，当海底介质为TI介质时海洋可控源电磁信号对高阻异常体的响应明显比各向同性的情况强。在远收发距时各向同性介质中高阻体的响应基本被空气波掩盖，而由于TI介质海底地层波衰减较慢，在海底附近与空气波相互抵消，使接收机能够接收到受干扰较少的高阻体中的导波；故在TI介质中有无异常体的振幅曲线差别比较大。这对浅海中进行MCSEM观测有用信号起着促进作用。
2.2.2 海底背景地层参考电导率张量绕x轴旋转时的电磁响应特征当海底背景地层参考电导率张量绕x轴旋转时，Ex分量同线振幅、相位及相对异常和相位差曲线呈现出的变化规律如图 7所示。由于本文中所列剖面均为沿y=0 m剖面结果，所以电流分布主要取决于海底介质x和z方向的电导率分布。当参考电导率张量沿x轴旋转时，改变的为y和z方向的电导率，σxz和σzx均为0，因此这种情况下电流分布主要取决于z方向电导率的大小。由图 7和图 8可以看出：当旋转角度不同时，电场振幅与相位和电流分布均与TI介质情况时类似。当旋转角度较小时，计算结果与上节TI结果接近；当旋转角度较大时，x和z方向电导率接近相等，计算结果与各向同性情况类似。综合上节TI介质中的结果可以看出海底地层波的大小受垂向电导率的影响较大。随着参考电导率旋转角度的减小，海底介质的垂向电导率逐渐减小，地层波在向海底附近传播时衰减较慢，海底地层波增强，待传到海底时与空气波相互抵消，进而在大收发距处高阻异常响应逐渐增大。
 |
| a.参考电导率张量绕x轴旋转30°的振幅响应；b.参考电导率张量绕x轴旋转60°的振幅响应；c.参考电导率张量绕x轴旋转30°的相位响应；d.参考电导率张量绕x轴旋转60°的相位响应；e.相对振幅异常；f.相位差。 图 7 参考电导率张量绕x轴旋转同线Ex振幅和相位曲线 Fig. 7 Amplitudes and phases of Ex for reference conductivity tensor rotated around x-axis |
| |
 |
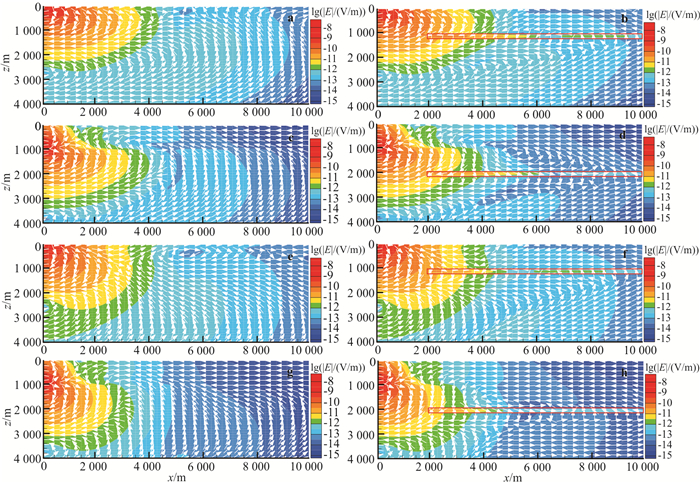| a.水深100 m参考电导率张量绕x轴旋转30°无异常体；b.水深100 m参考张量电导率绕x轴旋转30°有异常体；c.水深1 000 m参考电导率张量绕x轴旋转30°无异常体；d.水深1 000 m参考张量电导率绕x轴旋转30°有异常体；e.水深100 m参考电导率张量绕x轴旋转60°无异常体；f.水深100 m参考张量电导率绕x轴旋转60°有异常体；g.水深1 000 m参考电导率张量绕x轴旋转60°无异常体；h.水深1 000 m参考电导率张量绕x轴旋转60°有异常体。 图 8 海底地层参考电导率张量绕x轴旋转的电场及电流分布 Fig. 8 Distribution of E-field and current for reference conductivity tensor rotated around x-axis |
| |
当海底各向异性介质参考电导率张量绕y轴旋转时，电导率在xz平面内方向发生变化，σxz和σzx均有非零数值。由于海底地层波在海底接收机处方向与空气波方向一致，造成海底接收到的背景模型响应大幅度增加(图 9a、b和图 5a)。在大收发距，尤其是参考电导率旋转角度较大时，相位曲线基本趋于水平(图 9c、d)；这说明浅海情况下当背景底层的参考电导率绕y轴旋转时，大收发距处空气波对高阻体信号产生了较大干扰(图 9c、d)。对比图 10和图 8可以看出电流分布发生明显倾斜。另外，对比图 10a、e和图 6a、e可以得出结论：参考电导率张量绕y轴旋转后海底地层波增强，且其等值线与海底水平线夹角趋近于电阻率转角。对比图 5e和图 9e后认为，浅海情况TI介质中的高阻体导波最强，相对振幅异常最大。对比图 6中TI介质中的电流及电场强度分布，参考电导率绕y轴旋转后的海底地层波增强的区域更靠近海底，电流及电场分布沿横向拉伸较小，因此传到高阻层中的海底地层波没有明显增强，此时产生的相对异常变弱。随着旋转角度的增大，相对异常变得更小。与浅海情况相比，深海海洋电磁的海底地层波当旋转角较小时衰减减慢，对异常有一定掩盖作用，造成相对异常变小。随着旋转角度变大，海底地层波减弱，对异常的掩盖作用变得不明显，相对异常变大。对比前一小节分析的结果可知，在浅海情况下，当背景地层参考电导率的旋转主轴与测线方向一致时，高阻异常体的电磁响应较与测线方向垂直时强烈；故在进行数据解释时可以同时解释垂直测线方向的接收机的数据(等同于沿垂直方向进行观测)，以达到精确识别高阻异常体的目的。
 |
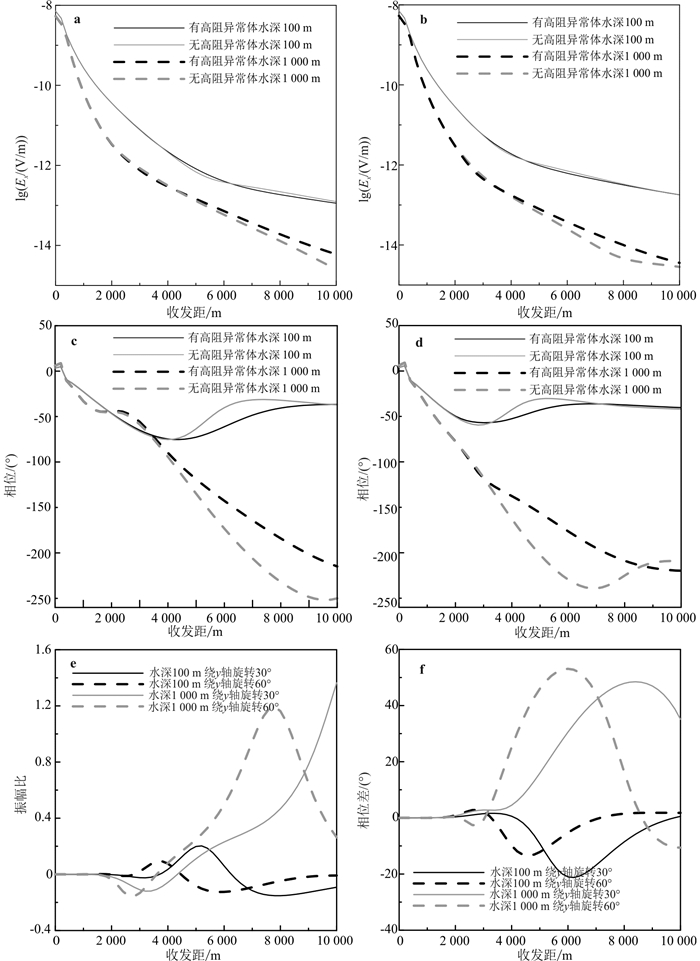| a.参考电导率张量绕y轴旋转30°的振幅响应；b.参考电导率张量绕y轴旋转60°的振幅响应；c.参考电导率张量绕y轴旋转30°的相位响应；d.参考电导率张量绕y轴旋转60°的相位响应；e.相对振幅异常；f.相位差。 图 9 参考电导率张量绕y轴旋转同线Ex振幅和相位曲线 Fig. 9 Amplitudes and phases of Ex for reference conductivity tensor rotated around y-axis |
| |
 |
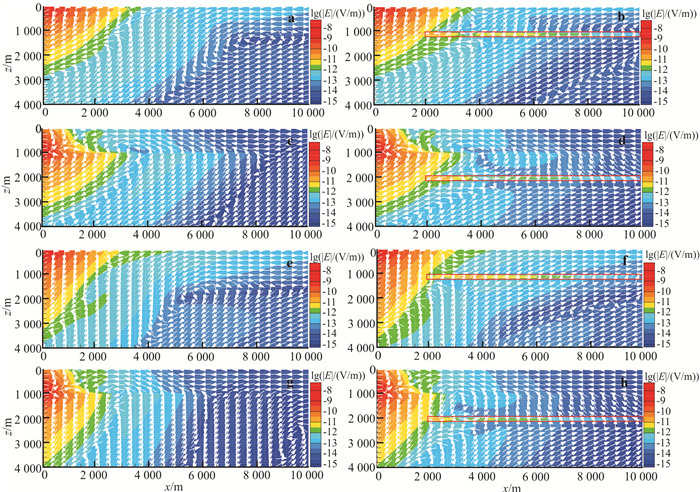| a.水深100 m参考电导率张量绕y轴旋转30°无异常体；b.水深100 m参考电导率张量绕y轴旋转30°有异常体；c.水深1 000 m参考电导率张量绕y轴旋转30°无异常体；d.水深1 000 m参考电导率张量绕y轴旋转30°有异常体；e.水深100 m参考电导率张量绕y轴旋转60°无异常体；f.水深100 m参考电导率张量绕y轴旋转60°有异常体；g.水深1 000 m参考电导率张量绕y轴旋转60°无异常体；h.水深1 000 m参考电导率张量绕y轴旋转60°有异常体。图 10 海底地层参考电导率张量绕y轴旋转的电场及电流分布 Fig. 10 Distribution of E-field and current for reference conductivity tensor rotated around y-axisLocation |
| |
本文基于有限差分技术实现了任意各向异性条件下海洋可控源电磁法的正演，并研究了任意各向异性介质中浅海区海洋电磁的响应特征。通过几组典型模型的计算可得出以下结论：
1)对于本文中100 m和1 000 m水深两种情况，空气波方向相反。
2)对于浅海情况：电磁信号中空气波占主导地位；而高阻层的导波在海底接收机处沿测线方向符号发生改变，因此其对空气波有叠加和抵消两种作用，造成无异常和有高阻异常两种情况下测量的曲线有交点，相对异常有正负。
3)电导率张量中各元素的变化对浅海和深海两种情况下海洋电磁响应相对异常大小的影响规律是相反的。
4)对比各种不同参考电导率张量旋转角的情况，浅海情况下TI介质中的高阻层导波最强，相对异常最大。
综上所述，各向异性介质中浅海与深海两种情况下的海洋电磁响应特征有较大区别，因此将深海海洋电磁数据的处理、反演和解释经验直接应用于浅海情况是不妥的。本文总结的几点结论对于海洋电磁数据的采集、处理与解释有一定指导意义，为浅海海洋电磁勘探方法的进一步发展提供了一定理论基础。
| [1] | Constable S C. Ten Years of Marine CSEM for Hydrocarbon Exploration[J]. Geophysics, 2010, 75(5):75A67-75A81. |
| [2] | Mittet R, Morten J P. The Marine Controlled-Source Electromagnetic Method in Shallow Water[J]. Geophysics, 2013, 78(2):E67-E77. |
| [3] | Andreis D, MacGregor L. Controlled-Source Electromagnetic Sounding in Shallow Water:Principles and Applications[J]. Geophysics, 2007, 73(1):F21-F32. |
| [4] | Løseth L O, Amundsen L, Jenssen A J. A Solution to the Airwave-Removal Problem in Shallow-Water Marine EM[J]. Geophysics, 2010, 75(5):A37-A42. |
| [5] | Chen J, Alumbaugh D L. Three Methods for Mitigating Airwaves in Shallow Water Marine Controlled-Source Electromagnetic Data[J]. Geophysics, 2011, 76(2):F89-F99. |
| [6] | 殷长春, 刘云鹤, 翁爱华, 等. 海洋可控源电磁法空气波研究现状及展望[J]. 吉林大学学报(地球科学版), 2012, 42(5):1506-1520. Yin Changchun, Liu Yunhe, Weng Aihua, et al. Research on Marine Controlled-Source Electromagnetic Method Airwave[J]. Journal of Jilin University (Earth Science Edition), 2012, 42(5):1506-1520. |
| [7] | Sasaki Y. 3D Inversion of Marine CSEM and MT Data:An Approach to Shallow-Water Problem[J]. Geophysics, 2012, 78(1):E59-E65. |
| [8] | Weiss C J, Constable S. Mapping Thin Resistors and Hydrocarbons with Marine EM Methods:Part II:Modeling and Analysis in 3D[J]. Geophysics, 2006, 71(6):G321-G332. |
| [9] | Kong F N, Johnstad S E, Røsten T, et al. A 2.5D Finite-Element-Modeling Difference Method for Marine CSEM Modeling in Stratified Anisotropic Media[J]. Geophysics, 2007, 73(1):F9-F19. |
| [10] | Weidelt P. 3-D Conductivity Models:Implications of Electrical Anisotropy[J]. Three-Dimensional Electromagnetics, 1999, 7:119-137. |
| [11] | Li Y, Dai S. Finite Element Modelling of Marine Controlled-Source Electromagnetic Responses in Two-Dimensional Dipping Anisotropic Conductivity Structures[J]. Geophysical Journal International, 2011, 185(2):622-636. |
| [12] | Wiik T, Ursin B, Hokstad K. 2.5 D EM Modelling in TIV Conductive Media and the Effect of Anisotropy in Normalized Amplitude Responses[J]. Journal of Geophysics and Engineering, 2013, 10(1):015006. |
| [13] | 殷长春, 贲放, 刘云鹤, 等. 三维任意各向异性介质中海洋可控源电磁法正演研究[J]. 地球物理学报, 2014, 57(12):4110-4122. Yin Changchun, Ben Fang, Liu Yunhe, et al. MCSEM 3D Modeling for Arbitrarily Anisotropic Media[J]. Chinese Journal of Geophysics, 2014, 57(12):4110-4122. |
| [14] | Newman G A, Commer M, Carazzone J J. Imaging CSEM Data in the Presence of Electrical Anisotropy[J]. Geophysics, 2010, 75(2):F51-F61. |
| [15] | Newman G A, Alumbaugh D L. Frequency-Domain Modelling of Airborne Electromagnetic Responses Using Staggered Finite Differences[J]. Geophysical Prospecting, 1995, 43(8):1021-1042. |
| [16] | 翁爱华, 刘云鹤, 贾定宇, 等. 基于电场不连续边界条件的层状介质电磁格林函数计算[J]. 吉林大学学报(地球科学版), 2013, 43(2):603-609. Weng Aihua, Liu Yunhe, Jia Dingyu, et al. Compute Green Function from Discontinuity of Trangential Electrical Fields Inside Source Contained Boundary[J]. Journal of Jilin University (Earth Science Edition), 2013, 43(2):603-609. |
| [17] | Yin C. MMT Forward Modeling for a Layered Earth with Arbitrary Anisotropy[J]. Geophysics, 2006, 71(3):G115-G128. |
| [18] | Weiss C J, Newman G A. Electromagnetic Induction in a Fully 3-D Anisotropic Earth[J]. Geophysics, 2002, 67(4):1104-1114. |
| [19] | Freund R W. A Transpose-Free Quasi-Minimal Residual Algorithm for Non-Hermitian Linear Systems[J]. SIAM Journal on Scientific Computing, 1993, 14(2):470-482. |
| [20] | Løseth L O, Ursin B. Electromagnetic Fields in Planarly Layered Anisotropic Media[J]. Geophysical Journal International, 2007, 170(1):44-80. |