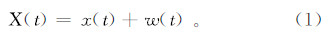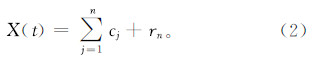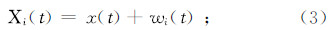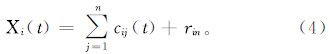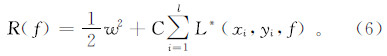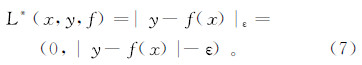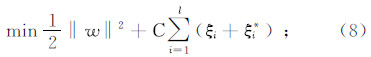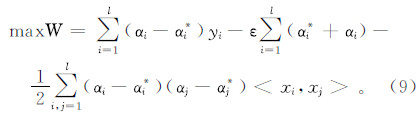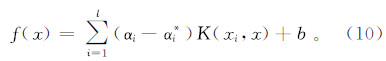Download PDF  
文章快速检索  
  高级检索
引用本文
秦喜文, 刘媛媛, 王新民, 等. 基于整体经验模态分解和支持向量回归的北京市PM2.5预测[J]. 吉林大学学报(地球科学版), 2016, 46(2): 563-568
Qin Xiwen, Liu Yuanyuan, Wang Xinmin, et al. PM2.5 Prediction of Beijing City Based on Ensemble Empirical Mode Decomposition and Support Vector Regression[J]. Journal of Jilin University(Earth Science Edition), 2016, 46(2): 563-568.
基于整体经验模态分解和支持向量回归的北京市PM2.5预测
秦喜文1,2,3, 刘媛媛2, 王新民2, 董小刚2, 张瑜2, 周红梅2    
1. 长春工业大学研究生院, 长春 130012;
2. 长春工业大学基础科学学院, 长春 130012;
3. 长春工业大学汽车工程研究院, 长春 130012
收稿日期: 2015-07-01
基金项目: 国家自然科学基金项目(11301036,11226335,51278065);吉林省教育厅科研项目(2014第127号,2013第142号)
作者简介: 秦喜文(1979-),男,副教授,主要从事HHT理论与应用方面的研究,E-mail:qinxiwen@ccut.edu.cn
通信作者: 王新民(1957),男,教授,主要从事数值分析方面的研究,E-mail:wxm@jlu.edu.cn
摘要: 为了更好地掌握大气中PM2.5浓度的变化规律,利用EEMD-SVR混合模型对该地区的PM2.5浓度值进行了短期预测。首先,通过采用整体经验模态分解(EEMD)方法分析北京市PM2.5,把原始时间序列分解成多个固有模态函数和趋势项;然后,对各阶固有模态函数进行周期性分析,揭示了北京市PM2.5的周期性变化特点;最后,对经过EEMD分解后的各阶固有模态函数和趋势项用支持向量机回归(SVR)方法进行预测。结果表明, EEMD-SVR混合模型比单一的SVR模型预测精度更高。
关键词: 整体经验模态分解     固有模态函数     周期性     支持向量机回归    
PM2.5 Prediction of Beijing City Based on Ensemble Empirical Mode Decomposition and Support Vector Regression
Qin Xiwen1,2,3, Liu Yuanyuan2, Wang Xinmin2 , Dong Xiaogang2, Zhang Yu2, Zhou Hongmei2    
1. Graduate School, Changchun University of Technology, Changchun 130012, China;
2. School of Basic Sciences, Changchun University of Technology, Changchun 130012, China;
3. Automotive Engineering Research Institute, Changchun University of Technology, Changchun 130012, China
Supported by National Natural Science Foundation of China (11301036,11226335,51278065) and Scientific Research Project of Jilin Province Department of Education (No.127 in 2014,No.142 in 2013)
Abstract: In order to obtain the pattern of variation of PM2.5 concentrations in the atmosphere in Beijing City, we build a EEMD-SVR hybrid model that can predict the PM2.5 level in a short term. Firstly, according to the ensemble empirical mode decomposition (EEMD) method to analyse the PM2.5 of Beijing City, the original time series is decomposed into the series of intrinsic mode functions (IMFs) and trend items; then, the periodic variation characteristics of PM2.5 is revealed through the periodic analysis of each intrinsic mode function;finally, we use support vector regression (SVR) to forecast all IMFs and trend items, which reflect the rationality of using SVR model. The results show that the prediction accuracy of mixed EEMD-SVR model is higher than single SVR model.
Key words: ensemble empirical mode decomposition     intrinsic mode functions (IMF)     periodicity     support vector regression    

0 引言

目前，我国处于快速发展阶段，社会的高速发展必然给环境带来诸多问题[1, 2, 3, 4]。近年来，大气环境污染问题较为严重，可吸入颗粒物对人体产生的危害也逐渐引起人们的关注[5]。尤其是PM2.5(指大气中直径小于或等于2.5 μm的颗粒物，也称为可吸入颗粒物)的污染成为近年来讨论的热点话题。虽然PM2.5只是地球大气成分中含量很少的组分，但它对空气质量和能见度等有重要的影响。与较粗的大气颗粒物相比，PM2.5直径小，富含大量的有毒、有害物质，且在大气中的停留时间长、输送距离远，对人体健康和大气环境质量的影响重大。因而，对PM2.5进行的研究有着非常重要的意义。一直以来，国内外对PM2.5的研究大都是针对其组成成分及其危害进行分析；近年来用统计分析的方法对其进行的研究也开始逐渐出现。张艺耀等[5]运用多元统计分析的方法对PM2.5进行了预测研究；张怡文等[6]采用神经网络的方法，通过O3、CO、PM10等空气污染物的观测指标，对PM2.5进行预测，并与通过多元统计的方法对PM2.5进行的预测相比较，发现运用神经网络模型的预测精度更高，但实验中也发现神经网络的预测模型要经过多次参数的调整(增加隐含层)，准确率才能得到提高，即以牺牲时间为代价来提高准确率；王敏等[7]采用BP人工神经网络模型对城市PM2.5进行预测，虽然其预测精度较高，但是其网络结构建立的优劣取决于设计者的经验知识，这给模型的建立带来很多的不确定性；Zhou Qingping等[8]在2014年采用了EEMD和GRNN混合模型对西安市的PM2.5进行预测，其预测精度虽然比只运用神经网络的方法高，但是，在对原始PM2.5数据进行分解后，再通过神经网络模型预测，依然要经过多次参数的调整，过程较为复杂，并且其预测值与真实值的相对误差大都在8%以上。

基于EEMD-SVR(ensemble empincal mode decomposition-support vector regression)方法是一种非线性、非平稳的自适应预测方法，并不需要复杂的调整参数的过程，预测精度高。本文利用EEMD-SVR混合模型对北京市的PM2.5进行短期预测，以期更好地掌握该地区短期内大气中PM2.5浓度的变化规律，为环保部门在治理PM2.5的过程中提供相关的决策建议。

1 EEMD方法

1998年，Huang Norden E等[9]提出了经验模态分解方法，本文使用的整体经验模态分解(EEMD)方法是对经验模态分解(EMD)方法的改进。此方法就是把若干均匀分布的白噪声加入原始信号，使其来补偿分解后所得固有模态函数(IMF)丢失的尺度，然后进行EMD的过程。本方法不仅抵消了加入的白噪声，还保留了原始序列的信号信息，这使得模态混合问题在一定程度上得到控制[9]。

EEMD具体步骤如下：

1)通过给待分析信号x(t)中加一组白噪声w(t)，构成信噪混合体

2)对信噪混合体X(t)进行EMD分解，分解成各个IMF分量的组合

式中：cj为第j个IMF；n为IMF的个数；rn为趋势项。

3)给待分析信号加入多组不同的白噪声wi(t)，得到

利用EMD方法分别对Xi(t)进行分解，得到不同组的IMF分量和趋势项:

式中：cij为第i组Xi(t)的第j个IMF；rin为第i组Xi(t)的趋势项。

4)对所有IMF组合相对应的IMF求平均：

其中,N表示添加白噪声序列的数目。通过上述步骤即得到最后的分解结果。而且因白噪声的零均值特性，加入噪声的次数足够多，将这些多次分解的结果取平均后，噪声最终将被互相抵消而达到消除的效果，总体平均的结果就可以被当作真实信号[10]。 2 SVR方法

支持向量机(support vector machine，SVM)是由Vapnik等[11]在1995年提出的方法，在20世纪90年代后期逐步成熟，现已广泛应用于机器学习和数据挖掘等领域。支持向量机的基本思想是：将作为输入的样本通过非线性变换到另一个更高维的特征空间，在这个特征空间中构造估计函数[12] 。本文所采用的SVR方法就是在SVM方法的推广下进行的。

SVR具体步骤：

给定l个独立同分布的样本(xi,yi),xi∈Rn,yi∈R,(i=1,2,…,l)。目标是找到一个最优函数f(x)=wx+b(其中：w，x∈Rn；b∈R)，使得泛函数R(f)取到最小值，这里，

式中：w2是结构风险；参数C是松弛因子，用来控制w的大小；L*(xi,yi,f)是ε的不敏感损失函数，定义为
其中：f是域X上的实值函数；x∈X；y∈R；ε为不敏感系数，用于控制拟合精度。引进松弛变量ξi和ξi*，则式(6)的最优化问题转化为
对应条件为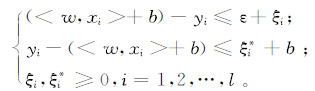
其中,<w，xi>为内积。式(8)是一个凸二次优化问题，引入拉格朗日函数，相应的对偶问题可用标准方法导出：
式中，αi，αi*为引入的拉格朗日乘子。

KKT(karush-kuhn-tucker)条件是非线性规划问题能有最优化解法的必要和充分条件，式(9)对应的KKT条件为

求解这个二次规划问题，得到最优的拉格朗日乘子αi,αi*以及b。

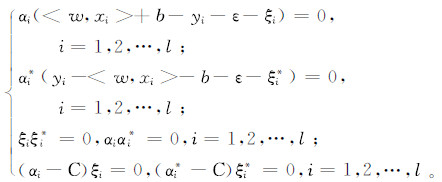
非线性时则把样本通过一个非线性映射映射到一个高维特征空间H上，将x变换为φ：Rd→H为φ(x)，然后在高维特征空间采用核函数进行回归，通过核函数，回归决策函数f(x)可直接表示为

式中，K(xi，x)为核函数。

据上述分析，求回归函数f(x)实际上可归结为求αi和αi*。可通过条件极小化f(x)确定αi和αi*。

3 基于整体经验模态分解和支持向量回归的北京市PM2.5预测 3.1 北京市PM2.5的EEMD分解

本文采用美国驻中国大使馆http://www.stateair.net/web/historical/1/1.html网站发布的2013年1月1日2014年9月29日北京市PM2.5质量浓度数据，共计638个，对其进行EEMD分解和分析。根据世界卫生组织所规定的标准[8]，每日空气质量级别和指数所对应的PM2.5日平均质量浓度见表 1。

表 1 空气质量表 Table 1 Air quality table
PM2.5日平均质量浓度(μg/m3)空气质量级别空气质量指数
0~50一级优
51~100二级良
101~150三级轻度污染
151~200四级中度污染
201~300五级重度污染
大于300六级严重污染
表选项

比较2013年和2014年的PM2.5质量浓度值(图 1)发现：2014年PM2.5质量浓度整体较2013年同期有所降低；PM2.5质量浓度在2013年11月中旬到次年3月中旬较高，这期间正好对应于北京市的法定供暖期。有关资料[13]表明：如果在冬季遇到长时间雾霾过程，通常在北方地区是由于采暖期的能源消耗排放增加，空气污染物逐渐累积导致的；而且，工业生产、机动车尾气、建筑施工等排放的二氧化硫、氮氧化物、挥发性有机物等有害颗粒物集中在一起,难以扩散，加上空气氧化性不断增强，导致污染因子活性增加，许多污染物发生复杂的化学反应生成PM2.5，也是造成PM2.5质量浓度升高的原因。而在4月份到10月份期间，PM2.5的质量浓度值都基本处于300 μg/m3以下，均未达到严重污染。

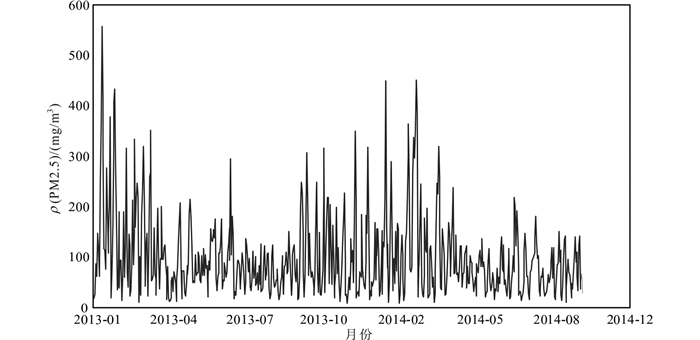图 1 北京市PM2.5数据时序图 Fig. 1 PM2.5 time series chart of Beijing City
图选项

针对2013年1月1日-2014年9月29日的PM2.5数据，利用MATLAB软件实现EEMD分解，共得到8个固有模态函数(IMF)和一个趋势项，固有模态函数需要满足如下两个条件：

1)数据极值点的数量与零点数相等或相差1个；

2)数据由极大值定义的上包络和由极小值定义的下包络的局部均值为0。

利用EEMD方法对北京市PM2.5时间序列进行处理，把原始序列分解成几个不同尺度的分量[14],并对每个分量进行研究，以便对北京市PM2.5的变化做出周期分析。从图 2可知：分解出的各阶IMF的波动频率从IMF2到IMF8逐渐降低，波动尺度越来越大，剩余的趋势项呈现出单调递减性；IMF2和IMF4的波动频率较大，反映出PM2.5的波动细节；IMF6和IMF8的波动尺度明显增大。从图 2中的趋势项还可以看出，北京市2013年1月到2014年9月期间的PM2.5数据经EEMD分解后的趋势项明显下降。

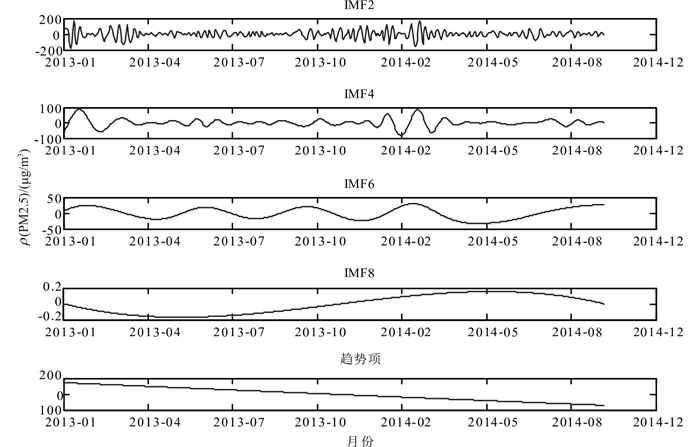图 2 部分固有模态函数和趋势项 Fig. 2 Part of the intrinsic mode function and trend
图选项
3.2 北京市PM2.5的周期性分析

本文采用平均周期法来计算经EEMD分解后的各阶IMF的周期，得到的各阶IMF的振荡周期可以更直观地观察到北京市PM2.5的周期性变化规律。平均周期法定义如下：

其中：T为变化周期；N1为总体数据数；N2为极小值点或极大值点数。笔者通过统计波峰和波谷的数量来计算北京市PM2.5的变化周期，结果如表 2所示。由表 2可知，各阶IMF的平均变化周期逐渐增大，并且北京市PM2.5的变化是按月或季度为周期变化的：IMF4的平均周期为30.23 d，说明变化周期是按月进行的；IMF6的平均周期为105.83 d，说明从长期看，周期性也是按季度变化进行的，即春夏秋冬各进行一次周期性变化。由此可知，北京市PM2.5变化的周期性非常明显。
表 2 各阶IMF的周期 Table 2 Period of each IMF
极大值数极小值数T/d
IMF11911913.32
IMF283847.60
IMF3424215.11
IMF4222130.23
IMF5131348.84
IMF666105.83
IMF733211.67
IMF833211.67
表选项
3.3 北京市PM2.5预测

本文运用MATLAB软件对前635个数据进行模拟预测，剩余的3个数据来检测模型的有效性。首先，对原始数据采用SVR方法预测；然后，采用EEMD-SVR的混合模型来对北京市PM2.5进行预测研究，即对经EEMD分解后得出的各阶固有模态函数和趋势项采用SVR方法进行模拟预测。预测结果见表 3。

表 3 SVR与EEMD-SVR预测值 Table 3 SVR and EEMD-SVR forecasting values
真实值/(μg/m3)SVR预测值/(μg/m3)误差/%EEMD-SVR预测值/(μg/m3)误差/%
85.58127.3448.8087.211.90
66.87109.9764.4568.372.24
52.33101.1293.2451.661.28
表选项

从表 3可以看出，EEMD-SVR混合模型对PM2.5进行短期预测的误差都在5.00%以下，说明预测的结果可信度高。因此，环保部门可以通过此方法来预测在未来两三天内PM2.5的质量浓度，以便对可能发生的重度环境污染带来的危害提前预警，进而调控一些社会活动。

4 结语

笔者以构建PM2.5预测模型为目标，利用EEMD方法对北京市PM2.5数据进行分解，对分解后的各阶IMF进行周期性分析，发现北京市PM2.5数据大致呈现出明显的周期性变化。各阶固有模态函数和趋势项利用SVR方法进行预测，预测结果比单纯利用SVR方法精度高。基于EEMD和SVR方法预测PM2.5具有重要的理论意义和实用价值，亦将在环境污染预测、地质灾害预测、金融风险预测等方面具有较好的推广应用。

笔者下一步将搜集空气中的二氧化硫、臭氧、API、PM10等相关指标，构建多元的PM2.5预测模型，为减轻空气中PM2.5污染提供科学依据和决策参考。

参考文献
[1] 刘贺,张弘强.基于粒子群优化神经网络算法的深基坑变形预测方法[J].吉林大学学报(地球科学版),2014,44(5):1609-1614. Liu He, Zhang Hongqiang. A Prediction Method for the Deformation of Deep Foundation Pit Based on the Particle Swarm Optimization Neural Network[J]. Journal of Jilin University(Earth Science Edition), 2014,44(5):1609-1614.
[2] 蒋玲玲,熊德琪,张新宇.大连滨海湿地景观格局变化及其驱动机制[J].吉林大学学报(地球科学版),2008,38(4):673-674. Jiang Lingling, Xiong Deqi, Zhang Xinyu. Change of Landscape Pattern and Its Driving Mechanism of the Coastal Wetland in Dalian City[J].Journal of Jilin University(Earth Science Edition),2008,38(4):673-674.
[3] 董志颖,李兵,孙晶.GIS支持下的吉林西部水质预警系统[J].吉林大学学报(地球科学版),2003,33(1):56-58. Dong Zhiying, Li Bing, Sun Jing. The Research of Forecast of Water Quality in the Western Part of Jilin Province by Means of GIS[J].Journal of Jilin University(Earth Science Edition),2003,33(1):56-58.
[4] 潘保芝, 石玉江, 蒋必辞.致密砂岩气层压裂产能及等级预测方法[J]. 吉林大学学报(地球科学版), 2015, 45(2):649-654. Pan Baozhi, Shi Yujiang, Jiang Bici.Research on Gas Yield and Level Predition for Post-Frac Tight Sandstone Reservoirs[J]. Journal of Jilin University(Earth Science Edition), 2015, 45(2):649-654.
[5] 张艺耀,苗冠鸿.影响PM2.5因素的多元统计分析与预测[J].资源节约与环保,2013(11):13-16. Zhang Yiyao, Miao Guanhong. The Factors Affecting PM2.5 and PM2.5 Forecasting Based on Multivariate Statistical Analysis[J].Resource Economization & Environment Protection, 2013(11):13-16.
[6] 张怡文,胡静宜,王冉.基于神经网络的PM2.5预测模型研究[J].江苏师范大学学报(自然科学版),2015, 33(1):63-65. Zhang Yiwen, Hu Jingyi, Wang Ran. PM2.5 Prediction Model Based on Neural Network[J].Journal of Jiangsu Normal University (Natural Science Edition), 2015, 33(1):63-65.
[7] 王敏, 邹滨, 郭宇. 基于BP人工神经网络的城市PM2.5浓度空间预测[J].环境污染与防治,2013,35(9):63-70. Wang Min, Zou Bin, Guo Yu. BP Artificial Neural Network-Based Analysis of Spatial Variability of Urban PM2.5 Concentration[J].Environmental Pollution & Control,2013,35(9):63-70.
[8] Zhou Qingping, Jiang Haiyan. A Hybrid Model for PM2.5 Forecasting Based on Ensemble Empirical Mode Decomposition and a General Gegression Neural Network[J]. Science of the Total Environment,2014, 496:264-274.
[9] Huang N E,Shen Z. The Empirical Mode Decomposition and Hillbert Spectrum for Nonlinear and Non-stationary Time Series Analysis[J]. Proceedings of the Royal Society London, 1998,454:903-995.
[10] Wu Zhaohua,Huang Norden E.A Study of the Ch-aracteristics of White Noise Using the Empirical Mode Decomposition Method[J].Proceedings of the Royal Society,2004, 460:1597-1611.
[11] Vapnik V. The Nature of Statistical Learning Theory[M]. New York:Springer-Verlag, 1995.
[12] 刘子阳,郭崇慧.应用支持向量回归方法预测胎儿体重[D].大连:大连理工大学,2005. Liu Ziyang, Guo Chonghui. Fetal Weight Prediction by Using Support Vector Regression[D].Dalian:Dalian University of Technology,2005.
[13] 范瑜,邹塞.徐州市春季PM10及PM2.5污染来源分析[J].环境科技,2014,27(2):49-52. Fan Yu, Zou Sai.Analysis of the PM10& PM2.5 Pollution Sources of Xuzhou in Spring[J].Environmental Science and Technology, 2014,27(2):49-52.
[14] 蔡赟姝,卢志明.基于经验模态分解的上证综合指数时间序列分析[J].上海大学学报(自然科学版),2012,18(4):384-389. Cai Yunshu, Lu Zhiming.The Shanghai Composite Index Time Series Analysis Based on Empirical Mode Decomposition[J].Journal of Shanghai University(Natural Science Edition),2012,18(4):384-389.
http://dx.doi.org/10.13278/j.cnki.jjuese.201602206
吉林大学主办、教育部主管的以地学为特色的综合性学术期刊
0

文章信息

秦喜文, 刘媛媛, 王新民, 董小刚, 张瑜, 周红梅
Qin Xiwen, Liu Yuanyuan, Wang Xinmin, Dong Xiaogang, Zhang Yu, Zhou Hongmei
基于整体经验模态分解和支持向量回归的北京市PM2.5预测
PM2.5 Prediction of Beijing City Based on Ensemble Empirical Mode Decomposition and Support Vector Regression
吉林大学学报(地球科学版), 2016, 46(2): 563-568
Journal of Jilin University(Earth Science Edition), 2016, 46(2): 563-568.
http://dx.doi.org/10.13278/j.cnki.jjuese.201602206

文章历史

收稿日期: 2015-07-01

相关文章

工作空间