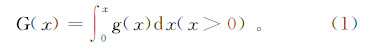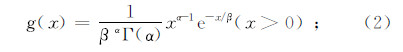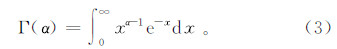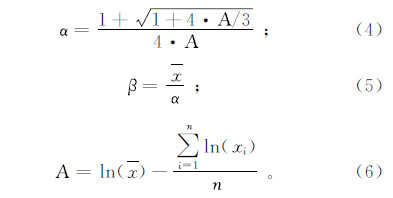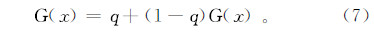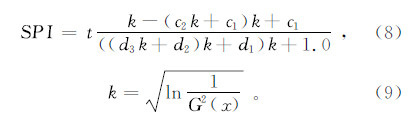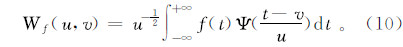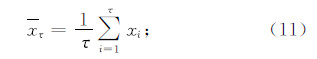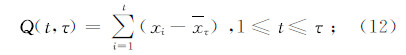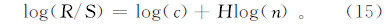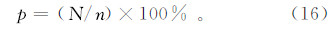0 引言
古往今来,干旱严重制约着社会经济的发展[1]。作为一种常见的自然灾害,干旱具有发生频率高、持续时间长和影响范围广的特点[2, 3]。各个学科领域对干旱定义不尽相同,一般可以把干旱分为气象干旱、农业干旱、水文干旱和社会经济干旱;气象干旱是所有干旱中发生最早的干旱,也是农业干旱的直接诱因之一[4, 5, 6]。
我国是农业大国,气象干旱长期困扰着农业生产。据报道,我国平均每年受旱面积约2 159.3万公顷,其中气象干旱约占60%,直接带来的粮食损失约100亿kg[7]。随着经济社会的迅速发展,全球气候有变暖的趋势,这将导致干旱进一步加重,从而对我国社会经济及人民生活造成严重的影响。
目前,在干旱研究方面,以标准化降水指数(standard precipitation index,SPI)为代表的气象干旱指标广泛地应用于世界各地,成为继帕默尔(Pamler)指数之后又一被广泛认可的干旱指数。SPI采用Γ函数的标准化降水量累计概率分布来划分干旱等级,资料获取容易,计算简单,能够很好地反映多时间尺度干旱的强度,使得使用同一干旱指标能够反映不同时间尺度和区域的干旱状况。R.Raja等、A.K.Mishra等、林盛吉等[8, 9, 10, 11, 12]分别应用SPI进行了干旱时空特征研究,并分析了SPI的适用性,结果表明,SPI能够很好地表征区域干旱的程度和持续时间。
吉林西部位于松嫩平原的西南部,该区十年九旱,干旱是对农业的最大威胁。然而在已有的文献报道中,鲜有基于季节性气象干旱指数法研究该区干旱的时空演化特征。因此,笔者以吉林西部为研究区,采用SPI作为气象干旱指数,利用Daubechies小波分析了研究区季节性干旱的时间演化趋势,使用R/S法分析了研究区季节性干旱的持续性,采用干旱频率法分析了研究区季节性干旱的空间分布特征,以期为研究区防旱减灾提供参考。
1 研究区概况及数据来源吉林西部位于松嫩平原西南部,地处半湿润到半干旱气候的过渡地带,兼有两个气候带的特性。地理坐标为123°09′E124°22′E,44°57′N45°46′N。全区以受内蒙古内陆气候带影响为主,具有显著的大陆性气候特征;年平均气温4.6 ℃,西南部较高,北部和东部较低;多年平均降水量为400~500 mm,受地理位置和地形地势的影响,降水时空分布不均,在时间上表现为夏季多而冬季少,夏季降水量占全年的71.2%,冬季则只占1.5%,在空间上表现为由西北向东南递增。
为研究吉林西部季节性气象干旱的时空演化特征,笔者收集了研究区6个气象站点(白城、通榆、长岭、乾安、前郭和扶余)19572010年的月降水量数据,数据来源于中国气象科学数据共享服务网。6个站点的地理位置分布及其降水序列如图 1所示。
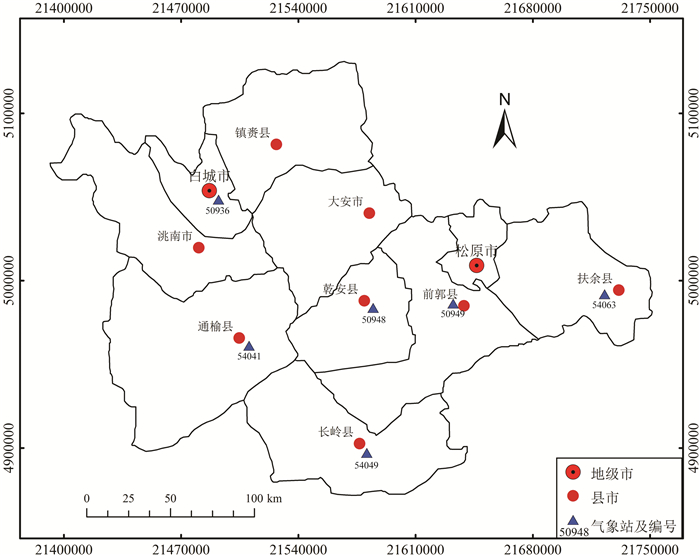 |
| 图 1 研究区气象站位置分布及其降水序列Fig.1 Distribution of meteorological stations and precipitation sequence in the study area |
标准化降水指数(SPI)是由McKee等[13]于1993年提出来的一种计算气象干旱的指标,它是实测降水量相对于降水概率分布函数的标准偏差。SPI采用Γ分布概率描述降水量的变化,将降水量进行正态标准化处理,利用累计频率表征某一时段降水量出现概率多少,最后用标准化累计频率来划分干旱等级。SPI具体计算过程及干旱等级[14, 15, 16]划分如下:
假设某一时间尺度下降水序列为x,则其累计概率可以表示为
式中:x为降水量数据;g(x)为Γ函数的概率密度函数。g(x)可以表示为
式中:α和β分别为形状参数和尺度参数;Γ(α)为Γ函数。
运用极大似然法估计α和 β的值:
式中:x为降水量的平均值;xi为某个时段内降水量;n为计算序列的长度。
由于G(x)在计算时不包含x=0的情况,而实际的降水量可以为0。因此,累计概率可以表示为
式中,q为降水量为0的概率。如果用m表示序列降水量为0的数量,则q=m/n。
累计概率G(x)通过下式转换为标准正态分布函数:
式中:t为概率密度的正负系数,当G(x)>0.5时,有G(x)=1-G(x),此时t=1;G(x)≤0.5时,t=-1。c1,c2,c3,d1,d2,d3为Γ(α)分布函数转化为累计概率的简化求解计算参数,其取值如下:
c1=2.515 517,c2=0.802 853,c3=0.010 328,
d1=0.189 269,d2=0.189 269,d3=0.001 308。
根据SPI值即可判断干旱等级[17],干旱等级划分见表 1。
| 干旱等级 | SPI |
| 无旱(1) | (-0.5,∞) |
| 轻旱(2) | (-1.0,-0.5] |
| 中旱(3) | (-1.5,-1.0] |
| 重旱(4) | (-2.0,-1.5] |
| 特旱(5) | (-∞,-2.0] |
小波变换用来分析信号的特征及性质,其实质是将信号投影到一系列小波基函数上,即将原信号分解为一系列小波基函数的组合[18, 19]:
式中:Wf(u,v)为小波变换系数;u为尺度因子;v为时间平移因子;f(t)为信号;Ψ为分析小波。
小波变换一般包括连续小波变换、离散小波变换和二进制小波变换。在实际工程中,对于时间序列处理通常使用离散小波变换。
小波分析存在低频波分析和高频波分析。一般而言,低频波用于分析时间序列整体上变化趋势,高频波则用来分析时间序列局部的变化趋势。
Daubechies小波是法国学者Daubechies根据紧支集正交小波步骤构造的一类以她姓名命名的小波,因其具有支集紧、正交性和光滑性而被广泛使用[20]。
2.3 重标极差分析重标极差分析(R/S)是英国水文专家赫斯特(Hurst)提出来的一种用于判断时间序列是随机游走还是有偏的随机游走的方法。该方法计算原理[21, 22, 23]如下:
假设某一时间序列xi,i=1,2,3,…,n,对于任意时刻τ≥1,定义该时间序列的均值序列为
在τ时刻序列xi累计离差为
极差为
标准差为
在上述计算出R(τ)和S(τ)基础上,定义R/S=R(τ)/S(τ),若R/S∝τH,则说明该序列存在Hurst现象,H即为Hurst指数。在实际计算中,H一般通过运用最小二乘回归法求解下面方程式得到:
其中,c是方程拟合过程中的常数。如果H>0.5,说明该序列未来变化与过去呈现正相关,即过程具有持久性,H愈接近1,持续性愈强;如果H=0.5,说明该序列随机游走,不存在相关性;如果H<0.5,说明序列未来变化与过去呈现负相关,即有突变跳跃逆转性,H愈接近0,突变性愈强。
3 结果与分析 3.1 标准化降水指数的时间演化特征分析根据标准化降水指数原理,利用MATLAB编制其计算程序,并计算各个站点春季(35月)、夏季(68月)、秋季(911月)、冬季(12月翌年2月)季节尺度的SPI值。使用Daubechies小波(低频波)分析了各站点季节尺度SPI在19582010年期间的变化趋势,分析结果如图 2所示。
 |
| 图 2 研究区季节性SPI的变化趋势Fig.2 Trend change of seasonal SPI in the study area |
从图 2中Daubechies小波(低频波)分析的结果可知:乾安、前郭和长岭春季和冬季的SPI有着上升趋势,夏季和秋季有降低趋势;扶余冬季的SPI有上升趋势,其他3个季节的SPI有降低趋势;白城和通榆秋季的SPI有降低趋势,而其他3个季节的SPI有上升趋势。值得注意的是:各站点在冬季SPI均有上升趋势,这意味着冬旱将随着时间推移得到减轻;而各站点在秋季SPI均表现为下降趋势,这表示秋旱将随着时间推移逐步加重。在分析了各站点季节性SPI趋势后,接着使用R/S法分析SPI在时间上的可持续性,分析结果见表 2。
| 站点 | H | |||
| 春季 | 夏季 | 秋季 | 冬季 | |
| 乾安 | 0.719 7 | 0.854 9 | 0.850 8 | 0.615 8 |
| 前郭 | 0.723 1 | 0.862 9 | 0.792 5 | 0.751 5 |
| 扶余 | 0.690 1 | 0.719 6 | 0.700 6 | 0.756 0 |
| 白城 | 0.733 7 | 0.659 4 | 0.729 3 | 0.652 3 |
| 通榆 | 0.850 8 | 0.909 1 | 0.845 8 | 0.592 7 |
| 长岭 | 0.779 9 | 0.890 1 | 0.643 7 | 0.698 5 |
由表 2可以看出,研究区6个站点各个季节的Hurst指数均大于0.500 0;这说明研究区的干旱状况呈现出长期持续性特征,即意味着研究区易出现多年无旱涝灾害或者多年持续性灾害。乾安(夏季和秋季)、前郭(夏季)、通榆(春季、夏季和秋季)和长岭(夏季)的Hurst指数均明显高于这些地区的其他季节和其他地区(白城市和扶余县)的4个季节;说明这些地区(季节)出现多年无旱涝灾害或者多年持续性灾害更加强烈。
3.2 标准化降水指数的空间分布特征分析为了讨论研究区季节性干旱状况的空间分布特征,首先统计出各站点4个季节发生干旱(包括轻旱、中旱、重旱和特旱)的次数;然后再计算出其发生的频率(表 3),并绘制各站点各季节干旱频率柱状图(图 3);最后使用arcgis绘制研究区4个季节干旱发生频率的空间分布图(图 4)。本文各站点各季节干旱的频率可用下式进行计算:
| 季节 | 干旱 等级 | 乾安 | 前郭 | 扶余 | 白城 | 通榆 | 长岭 | ||||||
| 次数 | 频率/% | 次数 | 频率% | 次数 | 频率% | 次数 | 频率% | 次数 | 频率% | 次数 | 频率% | ||
| 春季 | 轻旱 | 4 | 7.55 | 10 | 18.87 | 11 | 20.75 | 3 | 5.66 | 6 | 11.32 | 6 | 11.32 |
| 中旱 | 4 | 7.55 | 1 | 1.87 | 5 | 9.43 | 5 | 9.43 | 2 | 3.77 | 2 | 3.77 | |
| 重旱 | 1 | 1.87 | 2 | 3.77 | 1 | 1.87 | 1 | 1.87 | |||||
| 特旱 | 1 | 1.87 | |||||||||||
| 夏季 | 轻旱 | 10 | 18.87 | 9 | 16.98 | 12 | 22.64 | 7 | 13.21 | 9 | 16.98 | 7 | 13.21 |
| 中旱 | 1 | 1.87 | 3 | 5.66 | 4 | 7.55 | 5 | 9.43 | 1 | 1.87 | 2 | 3.77 | |
| 重旱 | 1 | 1.87 | 1 | 1.87 | 1 | 1.87 | 1 | 1.87 | |||||
| 特旱 | |||||||||||||
| 秋季 | 轻旱 | 12 | 22.64 | 8 | 15.09 | 5 | 9.43 | 10 | 18.87 | 9 | 16.98 | 4 | 7.55 |
| 中旱 | 5 | 9.43 | 7 | 13.21 | 5 | 9.43 | 4 | 7.55 | 5 | 9.43 | 9 | 16.98 | |
| 重旱 | 4 | 7.55 | 2 | 3.77 | 1 | 1.87 | 4 | 7.55 | 6 | 11.32 | 4 | 7.55 | |
| 特旱 | 2 | 3.77 | 2 | 3.77 | 5 | 9.43 | 3 | 5.66 | 1 | 1.87 | |||
| 冬季 | 轻旱 | 5 | 9.43 | 8 | 15.09 | 11 | 20.75 | 12 | 22.64 | 7 | 13.21 | 10 | 18.87 |
| 中旱 | 4 | 7.55 | 6 | 11.32 | 6 | 11.32 | 4 | 7.55 | 3 | 5.66 | 6 | 11.32 | |
| 重旱 | 1 | 1.87 | 2 | 3.77 | 2 | 3.77 | 2 | 3.77 | 2 | 3.77 | 7 | 13.21 | |
| 特旱 | 1 | 1.87 | 1 | 1.87 | 1 | 1.87 | 1 | 1.87 | 1 | 1.87 | |||
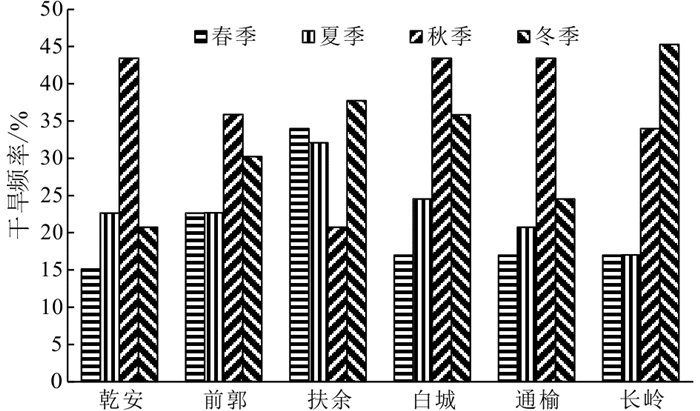 |
| 图 3 研究区季节性干旱发生频率柱状图Fig.3 Seasonal drought frequency histogram in study area |
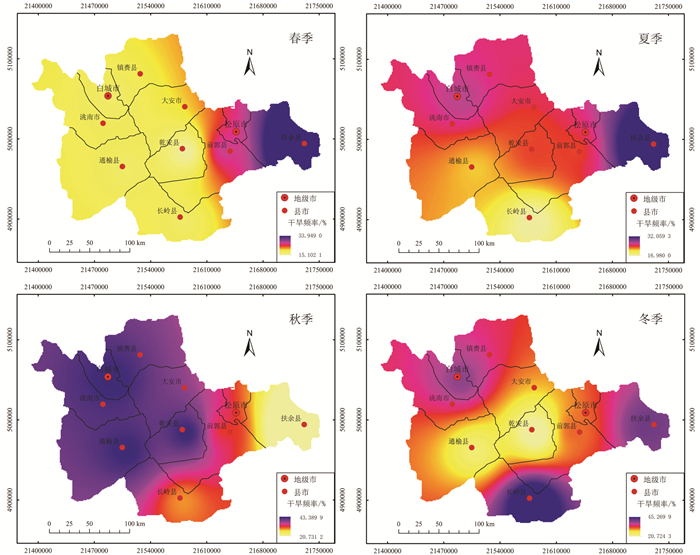 |
| 图 4 研究区季节性干旱频率空间分布图Fig.4 Spatial distributions of seasonal drought frequency in the study area |
式中:p为各种干旱发生的频率;N为各种干旱发生的次数。
由图 3和图 4可以看出:吉林西部春季干旱发生频率由西向东逐渐增大,干旱发生频率较高的地区为扶余;夏季干旱发生频率由西南向东北逐渐增大,干旱发生频率较高地区为扶余和白城;秋季干旱发生频率由东向西逐渐增大,干旱发生频率较高地区为白城、通榆、乾安、前郭和长岭;冬季干旱发生频率四周高,中间低,干旱发生频率较高为扶余、长岭和白城。由图 3和图 4还可以看出秋季是多个站点干旱发生的高频时期,这与SPI指数趋势分析结果基本一致。
SPI是根据降水的特点和变化特征,通过研究降水量统计分布规律定义的指数,该指数仅需降水量数据即可反映干旱强度和干旱持续性。但是该指数存在两处不足:其一是它未考虑蒸发、温度等其他气象因子;其二是它未通过干旱机理来反映干旱涉及的各个物理过程,如土壤水分蒸发、地表径流和地表水分补给等。限于篇幅限制,本文SPI指数结果未与通过干旱机理的多指标干旱指数(如Palmer干旱指数)进行对比,笔者会在以后研究中补充这一点。
4 结论1)研究区各站点冬旱整体上有减轻趋势,而秋旱有加重趋势。各站点干旱状况呈现出持续性特征,乾安(夏季和秋季)、前郭(夏季)、通榆(春季、夏季和秋季)、长岭(夏季)干旱持续性更加强烈。研究区春旱高频区为扶余,夏旱高频区为扶余和白城,秋旱高频区为白城、通榆、乾安、前郭和长岭,冬旱高频区为扶余、长岭和白城。
2)随着全球气候变暖,研究区气象干旱的时空分布产生新的变化,干旱可能会进一步加重。农业部门应当重视上述季节性气象干旱高频区以及气象干旱趋势加重季节,及早制定抗旱措施,以防干旱影响吉林西部农业生产发展。
| [1] | 蔡晓军, 茅海祥, 王文. 多尺度干旱指数在江淮流域的适应性研究[J]. 冰川冻土, 2013, 35(4):978-989. Cai Xiaojun, Mao Haixiang, Wang Wen. Study of the Adaptability of Multiscale Drought Indices in Yangtse-Huaihe River Basins[J]. Journal of Glaciology and Geocryology, 2013, 35(4):978-989. |
| [2] | 王莺, 李耀辉, 胡田田. 基于SPI指数的甘肃省河东地区干旱时空特征分析[J]. 中国沙漠, 2014, 34(1):244-253. Wang Ying, Li Yaohui, Hu Tiantian. Analysis on Spatial and Temporal Patterns of Drought Based on Standardized Precipitation Index in Hedong Area in Gansu Province[J]. Journal of Desert Research, 2014, 34(1):244-253. |
| [3] | 于磊, 杨井泉, 徐丽梅, 等. 气候变化背景下海河流域干旱特征及趋势[J]. 吉林大学学报(地球科学版), 2014, 44(5):1615-1624. Yu Lei, Yang Jingquan, Xu Limei, et al. Trend and Drying Characteristics of Haihe River Basin Under the Background of Climate Change[J]. Journal of Jilin University(Earth Science Edition), 2014, 44(5):1615-1624. |
| [4] | 陈社明, 卢文喜, 罗建男, 等. 吉林西部气象干旱的多标度分形特征[J]. 吉林大学学报(地球科学版), 2013, 43(1):245-250. Chen Sheming, Lu Wenxi, Luo Jiannan, et al. Multifractal Characteristic of Meteorological Drought in Western of Jilin Province[J]. Journal of Jilin University(Earth Science Edition), 2013, 43(1):245-250. |
| [5] | 詹存, 梁川, 赵璐. 川中丘陵区季节性干旱时空分布特征及成因分析[J]. 农业工程学报, 2013, 29(21):82-90. Zhan Cun, Liang Chuan, Zhao Lu. Temporal and Spatial Distribution Characteristics and Causes Analysis of Seasonal Drought in Hilly Area of Central Sichuan[J]. Transactions of the CSAE, 2013, 29(21):82-90. |
| [6] | 刘艳丽, 王国庆, 顾颖, 等. 基于改进的标准化降水指数的黄河中游干旱情势研究[J]. 干旱区资源与环境, 2013, 27(10):75-80. Liu Yanli, Wang Guoqing, Gu Ying, et al. Drought Trend Estimation Based on Improved Standard Precipitation Index for the Middle Reaches of Yellow River[J]. Journal of Arid Land Resources and Environment, 2013, 27(10):75-80. |
| [7] | 袁文平, 周广胜. 标准化降水指数与Z指数在我国应用的对比分析[J]. 植物生态学报, 2004, 28(4):523-529. Yuan Wenping, Zhou Guangsheng. Comparision Between Standardized Precipitation Index and Z Index in China[J]. Acta Phytoecologica Sinica, 2004, 28(4):523-529. |
| [8] | 黄晚华, 杨晓光, 李茂松, 等. 基于标准化降水指数的中国南方季节性干旱近58 a演变特征[J]. 农业工程学报, 2010, 26(7):50-59. Huang Wanhua, Yang Xiaoguang, Li Maosong, et al. Evolution Charateristics of Seasonal Drought in the South of China During the Past 58 Years Based on Standardized Precipitation Index[J]. Transactions of the CSAE, 2010, 26(7):50-59. |
| [9] | Raja R, Nayak A K, Panda B B, et al. Monitoring of Meteorological Drought and Its Impact on Rice(Oryza Sativa L.)Productivity in Odisha Using Standardized Precipitation Index[J]. Archives of Agronomy and Soil Science, 2014, 60(12):1701-1715. |
| [10] | 侯威, 张存杰, 高歌. 基于标准化降水指数的多尺度叠加干旱监测指标及其等级划分[J]. 干旱区研究, 2013, 30(1):74-88. Hou Wei, Zhang Cunjie, Gao Ge. Research on Multi-Scale Superposed Drought Index and Its Classification Based on Standardized Precipitation Index[J]. Arid Zone Research, 2013, 30(1):74-88. |
| [11] | Mishra A K, Desai V R. Drought Forecasting Using Stochastic Models[J]. Stoch Environ Res Risk Assess, 2005, 19:326-339. |
| [12] | 林盛吉, 许月萍, 田烨, 等. 基于Z指数和SPI指数的钱塘江流域干旱时空分析[J]. 水力发电学报, 2012, 31(2):20-26. Lin Shengji, Xu Yueping, Tian Ye, et al. Spatial and Temporal Analysis of Drought in Qiantang River Basin on Z Index and SPI[J]. Journal of Hydroelectric Engineering, 2012, 31(2):20-26. |
| [13] | 杜灵通. 基于多源空间信息的干旱监测模型构建[D]. 南京:南京大学, 2013. Du Lingtong. Drought Monitoring Model Based on Multi-Source Spatial Information and Its Application[D]. Nanjing:Nanjing University, 2013. |
| [14] | 任余龙, 石彦军, 王劲松, 等. 19612009年西北地区基于SPI指数的干旱时空变化特征[J]. 冰川冻土, 2013, 35(8):938-947. Ren Yulong, Shi Yanjun, Wang Jinsong, et al. Spatial and Temporal Variation Characteristics of Drought in Northwest China During 1961-2009 with Standardized Precipitation Index[J]. Journal of Glaciology and Geocryology, 2013, 35(8):938-947. |
| [15] | 刘艳平, 蔡焕杰. 三种干旱指标在径惠渠灌区的适用性分析[J]. 干旱地区农业研究, 2014, 32(4):236-241. Liu Yanping, Cai Huanjie. Suitability Analysis of Three Drought Indices in Jinghuiqu Irrigation District[J]. Agricultural Research in the Arid Areas, 2014, 32(4):236-241. |
| [16] | 马海娇, 严登华, 翁白莎, 等. 典型干旱指数在滦河流域的适用性评价[J]. 干旱区研究, 2013, 30(4):728-734. Ma Haijiao, Yan Denghua, Weng Baisha, et al. Applocability of Typical Drought Indexes in the Luanhe River Basin[J]. Arid Zone Research, 2013, 30(4):728-734. |
| [17] | GB/T 20481-2006气象干旱等级[S]. 北京:中国标准出版社, 2006. GB/T 20481-2006 Classification of Meterological Drought[S]. Beijing:China Standard Press, 2006. |
| [18] | Singh R, Khare A. Fusion of Multimodal Medical Images Using Daubechies Complex Wavelet Tran-sform:A Multiresolution Approach[J]. Information Fusion, 2014,19:49-60. |
| [19] | 孙德刚. 基于Daubechies小波和证据理论的声目标识别[J]. 中南大学学报(自然科学版), 2010, 41(4):1491-1496. Sun Degang. Acoustic Targets Fusion Identification Based on Daubechies Wavelet Transform and D-S Evidential Theory[J]. Journal of Central South University(Science and Technology), 2010, 41(4):1491-1496. |
| [20] | 陈东菊, 范晋伟, 张飞虎. 基于Daubechies小波和工件面形误差的机床导轨误差相关性分析[J]. 设计与研究, 2011(7):69-73. Chen Dongju, Fan Jinwei, Zhang Feihu. Correlation Analysis of the Guideway Error Based on the Daubechies Wavelet and Flatness of Workpiece[J]. Design and Research, 2011(7):69-73. |
| [21] | 万丽, 邓小成, 王庆飞, 等. 基于Hurst指数的矿化度强度识别:以山东大尹格庄金矿为例[J]. 吉林大学学报(地球科学版), 2013, 43(1):87-92. Wan Li, Deng Xiaocheng, Wang Qingfei, et al. Identification of Mineral Intensity Based on Hurst Index in Dayin'gezhuang Gold Deposit, Shandong Province, China[J]. Journal of Jilin University(Earth Science Edition), 2013, 43(1):87-92. |
| [22] | 周寅康, 张婕, 王腊春, 等. 长江下游地区近五百年洪涝序列的R/S分析[J]. 自然灾害学报, 1997, 6(2):78-83. Zhou Yinkang, Zhang Jie, Wang Lachun, et al. Rescaled Range Analysis of Flood Series in the Downstream Area of Yangtze River for Last 500-Years Period[J]. Journal of Natural Disasters, 1997, 6(2):78-83. |
| [23] | 冯新灵, 罗隆诚, 冯自立. 中国近50年降水变化趋势及突变的Hurst指数试验[J]. 干旱区地理, 2009, 32(6):859-866. Feng Xinling, Luo Longcheng, Feng Zili. Hurst Index Experiment on Precipitation Change Trend and Mutation of China in the Near 50 Years[J]. Arid Land Geography, 2009, 32(6):859-866. |