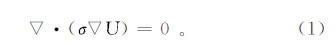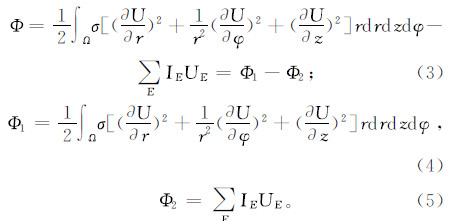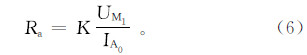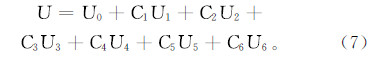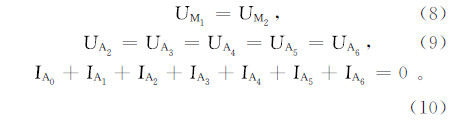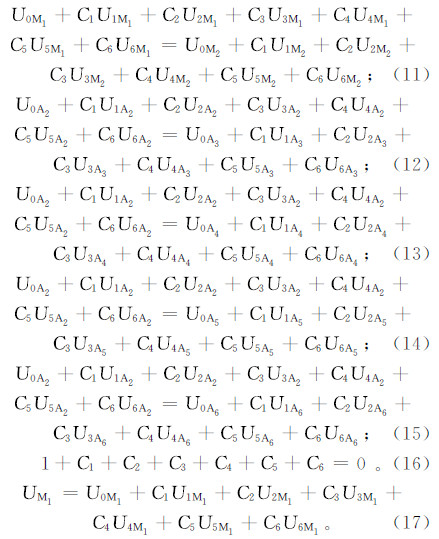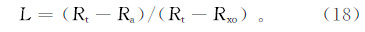2. 中国电波传播研究所, 河南 新乡 453003;
3. 大庆钻探工程公司测井公司, 黑龙江 大庆 163412;
4. 重庆地质矿产研究院, 重庆 400042
2. China Research Institute of Radiowave Propagation, Xinxiang 453003, Henan, China;
3. Wireline Logging Company, Daqing Drilling Engineering Company, Daqing 163412, Heilongjiang, China;
4. Chongqing Institute of Geology&Mineral Resources, Chongqing 400042, China
0 引言
水平井/大斜度井技术是油气勘探开发的重要技术，已经成为各大石油公司的重大战略措施之一。在水平井/大斜度井中，地层不具有旋转轴对称性，不能将问题简化到子午面上；原有混合法、解析方法等已经不适用于三维地层中，三维有限元方法可以有效地求取三维地层中的阵列侧向仪器响应[1, 2, 3, 4, 5]。对于阵列侧向测井而言，水平井/大斜度井中阵列侧向测井响应特征与直井下的阵列侧向测井响应差异较大。因此，对阵列侧向测井仪进行数值模拟不仅可以认识仪器的探测特征，为仪器研发提供一定的理论依据,而且可以为测井分析者更加清楚地认识测井曲线提供理论依据。笔者利用三维有限元方法计算阵列侧向测井响应，并对水平井/大斜度井中的阵列侧向测井响应特征进行分析。
1 阵列侧向电极系结构斯伦贝谢公司于1998年推出高分辨率新型阵列侧向测井仪(图 1)。仪器中间是主电流发射电极A0，两侧分别布置12对对称电极。在A0和屏蔽电极A1、A’1之间，有2对监督电极M1、M’1，M2、M’2；在屏蔽电极A1、A’1和A2、A’2之间，有2对监督电极M3、M’3，M4、M’4；在屏蔽电极A2、A’2和A3、A’3之间，有2对监督电极M5、M’5，M6、M’6；向外依次为A4、A’4，A5、A’5，A6、A’6。同命名号的电极等电位，例如M1与M’1等电位，以下不再赘述。
 |
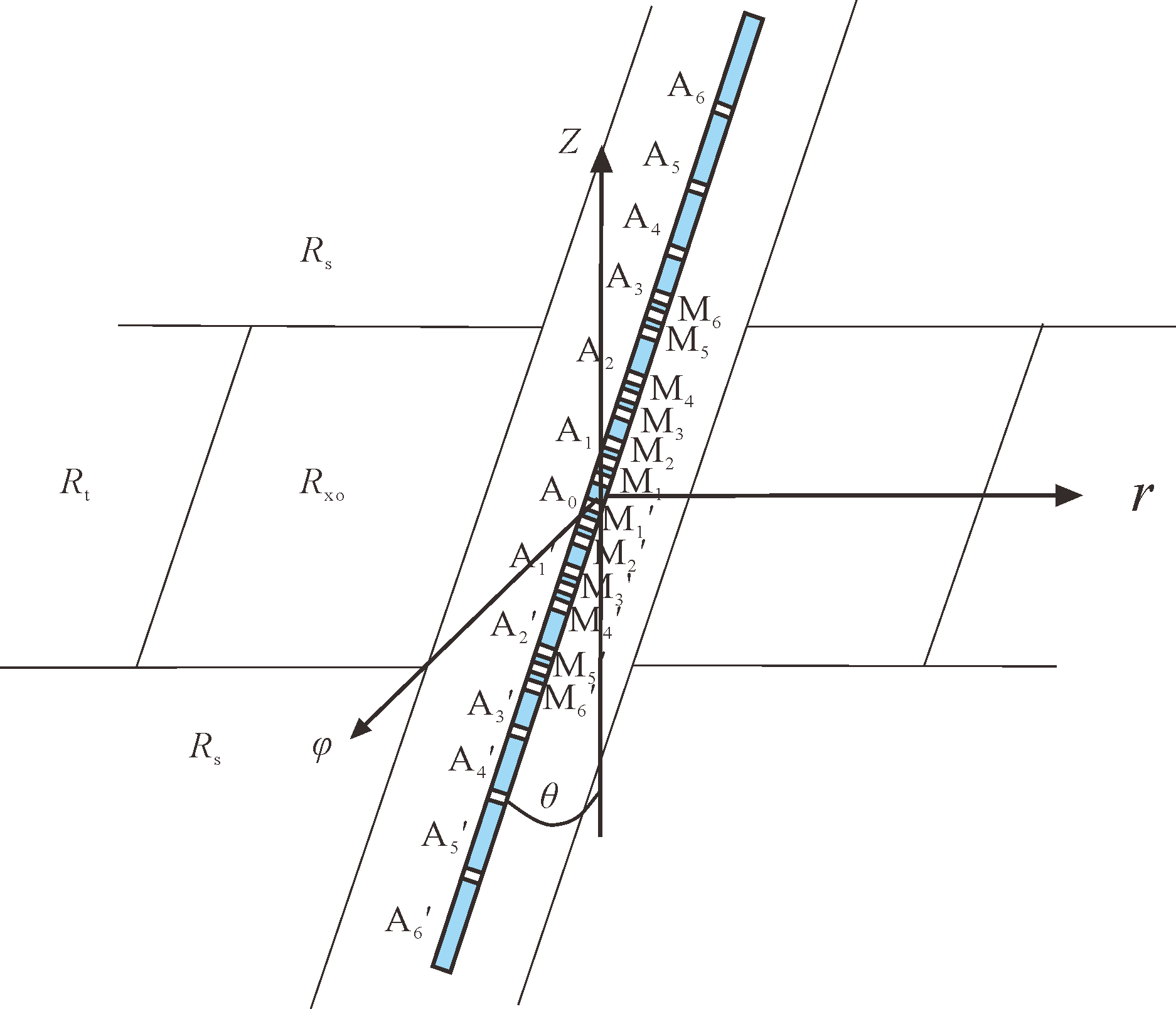| 图 1 阵列侧向仪器及地层模型Fig.1 Array lateral instruments and stratigraphic model |
当A0发射电流，其他屏蔽电极为回路电极时，测量得到泥浆电阻率RA0；从A0向两侧每增加1对屏蔽电极为发射电极时，得到探测深度不同的响应RA1、RA2、RA3、RA4、RA5。阵列侧向可以测量得到6条不同探测深度的电阻率曲线，其中探测最浅的主要反映泥饼电阻率的影响[6, 7, 8]。
图 1中给出了仪器与地层之间的关系。仪器与地层之间的夹角为θ，井眼大小为dh，泥浆电阻率为Rm，上下围岩电阻率为Rs，储层冲洗带电阻率为Rxo，目的层电阻率为Rt。
2 阵列侧向测井响应三维数值计算方法 2.1 泛函构造直流电测井采用低频交流电作为供电电源，由于其频率较低，阵列侧向测井响应可以归结为稳定电流场计算。阵列侧向测井的电场可由微分方程表示[9, 10, 11, 12, 13]：
式中：σ为地层电导率；U为测量电位。在柱坐标系(r,φ,z)下，可以表示为
第一类边界条件：在恒流电极上，U为未知常数；在恒压电极表面上，U为已知常数；在无穷远边界上，U=0。第二类边界条件：在恒流电极上，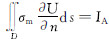
(IA为供电电极A的供电电流，σm是泥浆电导率，D为电极的表面，s为积分变量)；在绝缘边界面上，
。
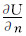为求取方程(2)，需将偏微分方程问题转化成求泛函的极值问题[14, 15]：
式中：IE，UE是各电极上电流和电位；E为电极的边界；Ω为所求取地层的边界。通过有限元方法求得电位后，阵列侧向测井响应值满足
式中：K为仪器电极系常数；UM1为M1电极上的电位值；IA0为仪器A0电极发射电流强度；Ra为不同条件下的视电阻率。
2.2 电场叠加在求解阵列侧向电位分布时，采用电场叠加原理，将其化为多个相应场的电位函数迭加。
第一个分场只有A0电极发射单位电流I=1，其他电极均不发射电流；从第二个分场开始，第n个分场只有An－1、An－1’电极发射单位电流I=1，其他电极均不发射电流，An－1、An－1’电极等电位(2≤n≤7)。依次计算得到第一到第七分场电位U0(x,y,z)、U1(x,y,z)、U2(x,y,z)、U3(x,y,z)、U4(x,y,z)、U5(x,y,z)、U6(x,y,z)，则阵列侧向电位为
式中：C1、C2、C3、C4、C5、C6为聚焦合成系数。
下面以RA1为例对阵列侧向工作模式的约束条件进行论述，其约束条件为
式中：UM1，UM2为电极M1、M2的电位值；UA2，UA3，UA4，UA5，UA6为电极A2、A3、A4、A5、A6的电位值；IA0，IA1，IA2，IA3，IA4，IA5，IA6为电极A1、A2、A3、A4、A5、A6的电流值。
利用式(8)(10)的约束条件，可以求出各分场的聚焦合成系数：
式中： UiM1、UiM2、UiA2、UiA3、UiA4、UiA5、UiA6为第i1分场下各个电极的电位值。
将公式(6)代入公式(11)中可以得到视电阻率RA1的电阻率值，通过不同的聚焦方法可以得到RA2、RA3、RA4、RA5的电阻率值。
2.3 均匀地层电场分布模拟条件：均匀地层电阻率为1 Ω·m，仪器半径为0.045 m。由模拟结果(图 2)可知，随着屏蔽电极数的增多，在相同的位置处地层的电位值逐渐增大，仪器的探测范围也逐渐增大。
 |
| a.RA5响应；b.RA4响应；c.RA3响应；d.RA2响应；d.RA1响应。图 2 均匀地层下不同测量方式的电位分布Fig.2 Electric potential distribution of different measurement of homogeneous formation |
根据表 1所示的地层模型，井径dh=20.32 cm，计算阵列侧向测井的伪几何因子，并确定其探测深度。伪几何因子为
| 地层类型 | Rt/(Ω·m) | Rxo/(Ω·m) | Rm/(Ω·m) |
| 地层1(低侵) | 1 | 10 | 0.1 |
| 地层2(高侵) | 50 | 10 | 0.1 |
| 注：H为目的层厚度；Rb为围岩电阻率。 | |||
以50%伪几何因子来定义仪器的探测深度，如图 3所示。阵列侧向测井在高侵模拟条件下5种探测方式的探测深度分别为：RA5 0.70 m，RA4 0.45 m，RA3 0.37 m，RA2 0.29 m，RA1 0.23 m。阵列侧向测井在低侵模拟条件下5种探测方式的探测深度分别为：RA5 0.75 m，RA4 0.54 m，RA3 0.45 m，RA2 0.38 m，RA1 0.30 m。
 |
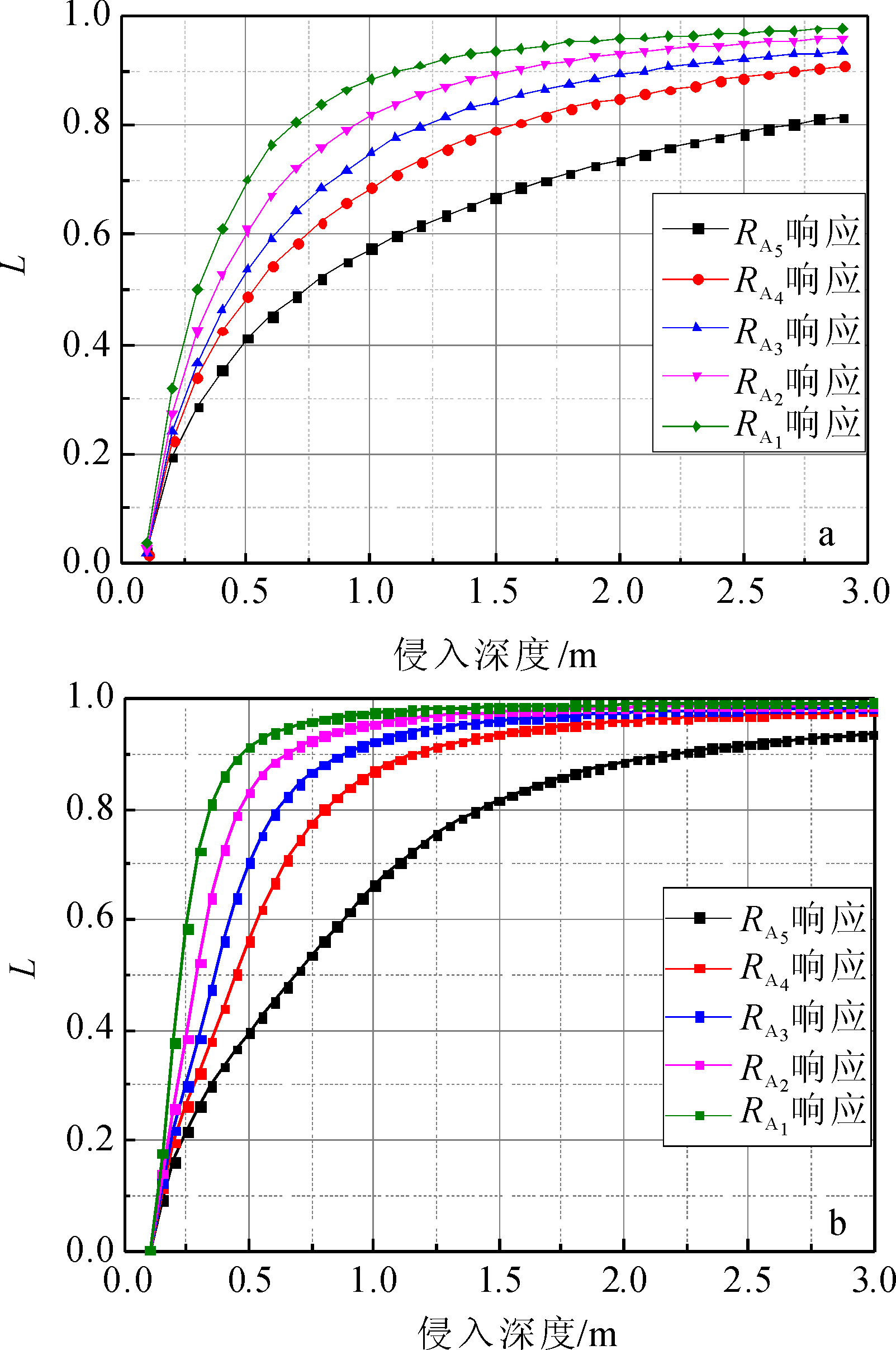| 图 3 低侵地层(a，地层1)和高侵地层(b，地层2)阵列侧向伪几何因子Fig.3 Array lateral pseudo geometrical factor of low invasion formation (a,Formation 1) and high invasion formation (b,Formation 2) |
阵列侧向测井探测深度要小于斯伦贝谢CSU(cyber service unit)深侧向测井的探测深度(1.27 m)，但是阵列侧向测井优势在于反映地层电阻率径向的渐变，可以在径向进行电阻率剖面成像。
3.2 井斜影响根据表 2所示的地层模型，模拟两种地层模型在不同井斜条件下的阵列侧向测井响应。井斜依次为0°、15°、30°、45°、60°、75°、90°，模拟结果见图 4、图 5。表 2 地层模型
| 地层类型 | Rt/ (Ω·m) | H/ m | Rb/ (Ω·m) | Rm/ (Ω·m) |
| 地层3(低侵) | 20 | 1 | 3 | 1 |
| 地层4(高侵) | 3 | 1 | 20 | 1 |
| 注：H为目的层厚度；Rb为围岩电阻率。 | ||||
从图 4中可以看出，对于1 m厚的地层，在井斜为0°时为直井，由于阵列侧向测井具有分辨率高的优势(分辨率为0.4 m)，可以很好地反映地层信息，探测深度最深的RA5响应值为18.1 Ω·m。随着仪器探测深度的降低，探测深度浅的仪器受井眼和围岩的影响较大，从而使RA4、RA3、RA2、RA1测量值依次下降。当井斜小于15°时，井斜对阵列侧向测井响应的影响可以忽略；随着井斜角度的逐渐增大，地层中点的阵列侧向电阻率明显降低；在井斜超过60°时，阵列侧向测井响应值下降为直井中的阵列侧向响应的70%，运用此时的电阻率信息代入到阿尔奇公式计算含水饱和度，必定会带来极大的误差。井斜的增大对探测深度最深的RA5影响最大，对探测深度最浅的RA1影响最小。
 |
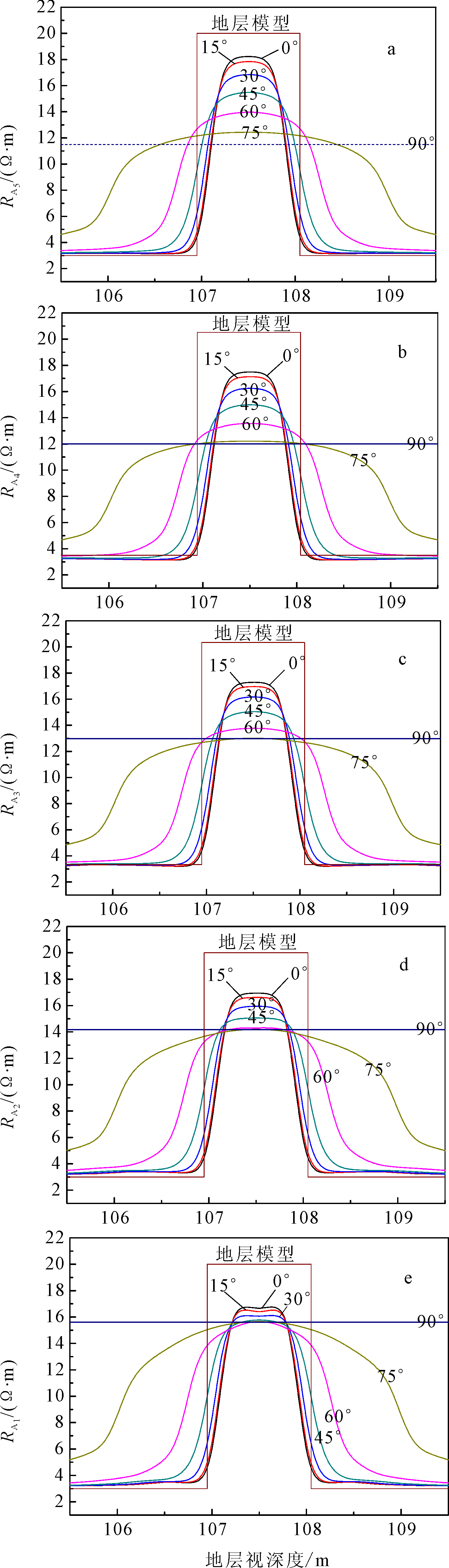| 图 4 厚1 m的高电阻率地层(地层3)阵列侧向测井响应Fig.4 Array lateral log response of 1 m thick and high resistivity formation(Formation 3) |
从图 5中可以看出，对于低电阻率泥岩层，当地层厚度为1 m、井斜为0°时，探测深度最深的RA5响应曲线测量值接近目的层的电阻率，而随着探测深度的减小，RA4、RA3、RA2、RA1测量值受围岩影响较大，响应值依次增大。当井斜小于15°时，井斜对于阵列侧向响应的影响可以忽略；随着井斜角度的增大，地层中点的阵列侧向电阻率也逐渐增大，阵列侧向测井响应受围岩的影响变大；井斜同样对于探测深度最大的RA5影响最大，对于探测深度最小的RA1影响较小。
 |
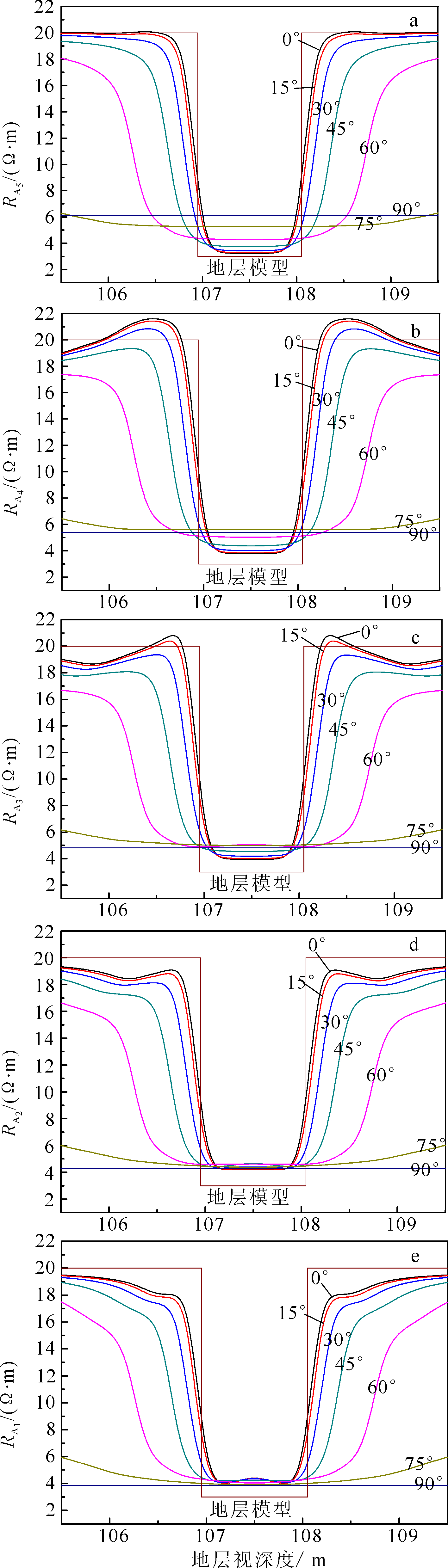| 图 5 厚1 m的低电阻率地层(地层4)阵列侧向测井响应Fig.5 Array lateral log response of 1 m thick and low resistivity formation(Formation 4) |
对于斜井中，测井资料校正一般仅是对地层视厚度进行校正，对于井斜与侵入纵向影响研究较少。下面主要考虑不同倾斜井中阵列侧向测井响应值和侵入深度及井斜角的关系，地层模型如表 3所示。
| 地层类型 | Rt/ (Ω·m) | H/ m | Rb/ (Ω·m) | Rm/ (Ω·m) | Rxo/ (Ω·m) |
| 地层5(低侵) | 20 | 1 | 3 | 1 | 7 |
| 地层6(高侵) | 7 | 1 | 3 | 1 | 20 |
井斜依次为0°、15°、30°、45°、60°、75°、90°，侵入半径0~1.9 m，地层5、6模拟结果如图 6、图 7所示。
 |
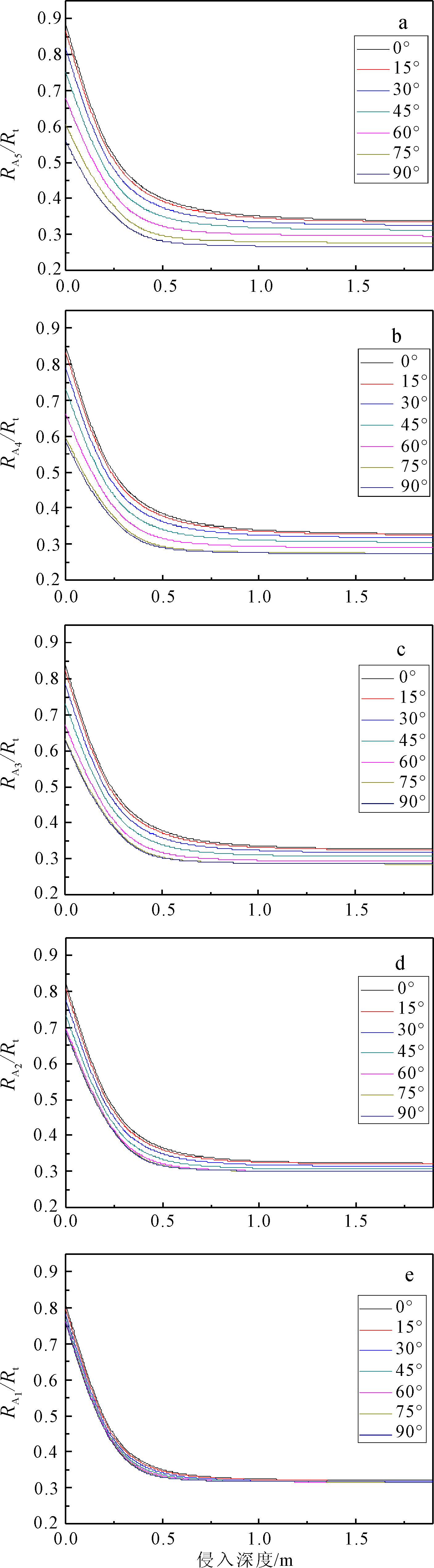| 图 6 厚度1 m的低侵地层(地层5)阵列侧向测井响应Fig.6 Array lateral log response of 1 m thick and low invasion formation(Formation 5) |
 |
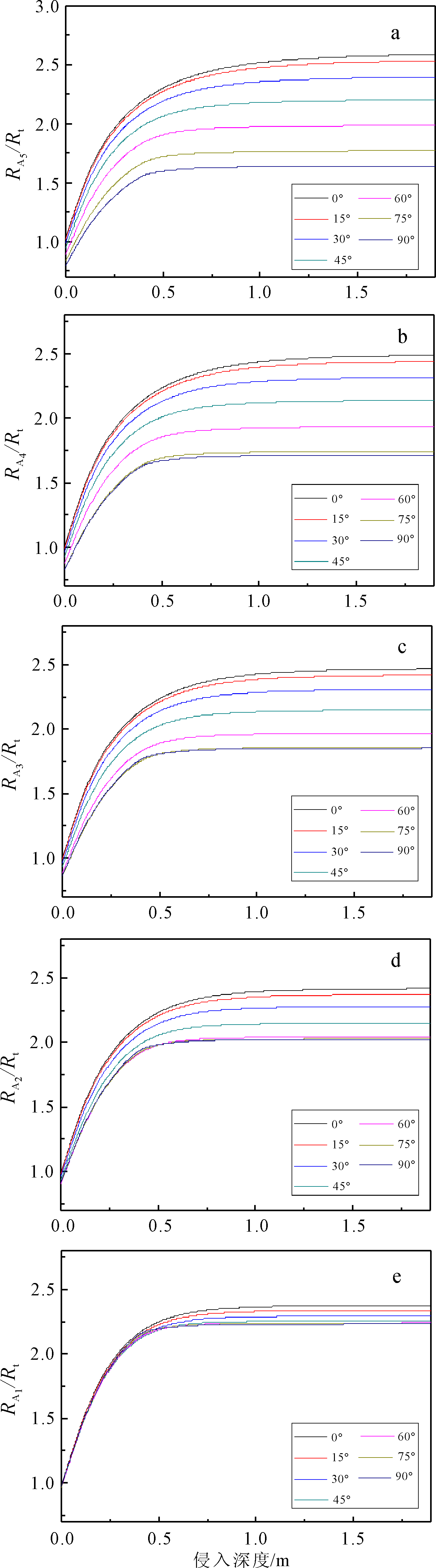| 图 7 厚度1 m的高侵地层(地层6)阵列侧向测井响应Fig.7 Array lateral log response of 1 m thick and high invasion formation(Formation 6) |
由图 6可见，对于低侵地层，在井斜小于15°范围以内，即使存在侵入，井斜角的影响可以忽略。随着侵入深度的增大，视电阻率与地层电阻率的比值逐渐降低；在同样的侵入深度，随着井斜角的增大，视电阻率与地层电阻率的比值同样出现单调下降的趋势。在低侵地层中的阵列侧向5条响应曲线，RA5受井眼与井斜的影响最大，RA1受井眼井斜的影响最小。由图 7可见，对于高侵地层，在井斜小于15°范围以内，井斜角的影响同样可以忽略。随着侵入深度的增大，视电阻率与地层电阻率的比值逐渐增大；在同样的侵入深度，随着井斜角的增大，视电阻率与地层电阻率的比值出现单调增大的趋势。在高侵地层中的阵列侧向5条响应曲线，RA5受井眼与井斜的影响最大，RA1受井眼井斜的影响最小。
4 结论1)三维有限元方法可以计算水平井/大斜度井中的阵列侧向测井响应，可以进行三维地层环境中的影响因素分析。
2)阵列侧向探测深度要小于CSU深侧向探测深度，但是阵列侧向可以在径向进行电阻率剖面成像，从而更加直观地反映地层电阻率变化过程。
3)井斜对于阵列侧向测井响应的影响主要体现在地层的分界面附近，随着井斜角的增大，围岩影响也逐渐增大，井斜对探测深度最深的响应曲线影响要大于探测深度最小的响应曲线。
4)在井斜小于15°存在侵入时，水平井/大斜度井中井斜影响可以忽略。
5)在水平井/大斜度井中，必须进行井斜校正，否则会影响到计算含水饱和度的准确性。
| [1] | 李善军,肖永文,汪涵明,等.裂缝的双侧向测井响应的数学模型及裂缝孔隙度的定量计算[J].地球物理学报,1996,39(6):845-852. Li Shanjun,Xiao Yongwen,Wang Hanming,et al. Mathematical Model of Dual Laterolog Response to Fracture and Quantitative Interpretation of Fracture Porosity[J]. Acta Geophysica Sinica, 1996, 39(6): 845-852. |
| [2] | 李善军.用三维有限元素法反演单一灰岩裂缝性储层的裂缝孔隙度和裂缝倾角[J].测井技术,1998,22(6):412-415. Li Shanjun.Inverting Fracture Porosity and Dip of Limestone Fractured Reservior Using 3-D FEM[J].Well Logging Technology, 1998, 22(6): 412-415. |
| [3] | 刘福平,李善军,张庚骥.利用积分方程法计算双侧向测井仪的井眼校正曲线[J].地球物理学报,1997,40(6):857-866. Liu Fuping,Li Shanjun,Zhang Gengji.Computation of Borehole Correction Curves of Dual Laterolog Tool by Integral Equation Method[J]. Acta Geophysica Sinica, 1997, 40(6): 857-866. |
| [4] | 刘振华,胡启,张建华.用有限元法计算侵入条件下双侧向测井仪器响应[J].石油仪器,1994,8(3):149-152. Liu Zhenhua,Hu Qi,Zhang Jianhua.Calculating Intrusion by the Finite Element Method Under the Condition of Dual Laterolog Tool Response[J]. Petroleum Instruments, 1994, 8(3): 149-152. |
| [5] | Chemali R, Gianzero S, Su S M.The Dual Laterolog in Common Complex Situations[C]// SPWLA 29th Annual Logging Symposium. San Antonio: [s.n.], 1988: 5-8. |
| [6] | Chen Y H, Chew W C, Zhang H J. A Novel Array Latero Log Method[J]. Log Analyst, 1998, 39(1): 23-30. |
| [7] | Smits J W, Dubourg I, Luling M G, et al. Improved Resistivity Interpretation Utilizing a New Array Laterolog Tool and Associated Inversion Processing[C]//Annual Technical Conference and Exhibition of the Society of Petroleum Engineers. New Orleans: SPE, 1998: 831-844. |
| [8] | 邓少贵,李智强,陈华.煤层气储层裂缝阵列侧向测井响应数值模拟与分析[J].煤田地质与勘探,2010,38(3):55-60. Deng Shaogui,Li Zhiqiang,Chen Hua.The Simulation and Analysis of Lateral Log Response of Fracture in Coalbed Methane Reservior[J]. Coal Geology & Exploration, 2010, 38(3): 55-60. |
| [9] | 李智强,范宜仁,邓少贵,等.基于改进差分进化算法的阵列侧向测井反演[J].吉林大学学报:地球科学版,2010,40(5):1199-1204. Li Zhiqiang,Fan Yiren,Deng Shaogui,et al. Inversion of Array Laterolog by Improved Difference Evolution[J]. Journal of Jilin University: Earth Science Edition, 2010, 40 (5): 1199-1204. |
| [10] | 朱大伟,邓少贵,范宜仁,等.大斜度井双侧向测井响应数值模拟研究[J].测井技术,2005,29(3):208-211. Zhu Dawei, Deng Shaogui, Fan Yiren, et al. Numerical Simulation of Dual Laterolog Response in Highly Deviated Wells[J]. Well Log Technology, 2005, 29(3): 208-211. |
| [11] | 李大潜.有限元素法在电法测井中的应用[M].北京:石油工业出版社,1980:72-129. Li Daqian. Finite Element Method in the Application of the Electrical Logging[M]. Beijing: Petroleum Industry Press, 1980: 72-129. |
| [12] | Clavier C.The Challenge of Logging Horizontal Wells[J]. Log Analyst, 1991, 32(2): 63-84. |
| [13] | Sibbit A M, Faivre O. The Dual Laterolog Response in Fractured Rocks[C]// SPWLA 26th Annual Logging Symposium. Dallas: [s.n.], 1985: 17-20. |
| [14] | 张庚骥.电法测井[M].东营:石油大学出版社,1996. Zhang Gengji. Electrical Logging[M]. Dongying: University of Petroleum Press, 1996. |
| [15] | 高杰,谢然红.大斜度井侧向测井三维正演数值模拟及曲线快速校正方法研究[J].石油勘探与开发,2000,27(2):69-71. Gao Jie, Xie Ranhong. 3D Numerical Forward Modeling and Fast Correction of Dual-Laterolog for High Angle Deviated Wells[J]. Petroleum Exploration and Development, 2000, 27(2): 69-71. |