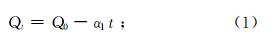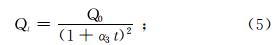2. 国土资源部岩溶动力学重点实验室, 广西 桂林 541004
2. Key Laboratory of Karst Dynamics, Ministry of Land Resources, Guilin 541004, Guangxi, China
0 引言
岩溶含水系统的高度非均质性和各向异性使得定量计算含水层水文地质参数十分困难。传统的野外方法如抽水试验、注水试验和微水试验等方法能够描述孔隙介质含水层特性,而对岩溶管道含水系统却难以准确刻画[1, 2]。由于岩溶区泉流量衰减曲线是岩溶含水层形态特征和水力特性的综合反映,因此研究流量衰减曲线是推求岩溶水文地质参数的重要手段。1965年,Schoeller[3]针对岩溶系统,根据不同介质类型分析了岩溶泉流量曲线特征;1997年,Eisenlohr等[4]通过数值模型模拟了岩溶泉流量曲线,结果表明运用不同物理方程描述曲线的不同阶段能够更好地体现岩溶泉流量特点;2003年,Dewandel等[5]对泉流量衰减的机制和理论工作进行了总结,但在水文地质参数估算方面有所欠缺;2011年,Fiorillo[6]利用水箱模型研究了岩溶泉流域衰减曲线,并于2014年[7]总结分析了岩溶泉流量衰减曲线的经验公式和物理模型,对岩溶泉流量衰减的过程和机理进行了系统的阐述。国内对这方面的研究相对较少:1984年,林敏[8]探讨了流量衰减方程系数的物理意义;2010年,张艳芳等[9]基于Boussinesq方程计算了后寨河流域的水文地质参数;2015年,束龙仓等[10]利用物理模型和数值模拟技术研究了岩溶泉流量影响因素和作用机制。然而,以上研究在运用泉流量衰减曲线估算水文地质参数方面仍有所欠缺。笔者应用流量衰减分析理论,针对岩溶区特点,计算寨底岩溶地下河系统水文地质参数,以期为该地区地下水的科学管理和资源评价提供依据。
1 理论方法在岩溶发育地区,一次完整的泉流量曲线包括5个阶段[7](图1):第一阶段(①)表明在没有补给情况下,泉流量有逐渐下降趋势;第二阶段(②)是在一次强降雨过程后,由于地表入渗至岩溶含水层而表现的一次流量峰值;第三阶段(③)泉流量主要来源于岩溶管道内的水量;第四阶段(④)泉流量主要来源于岩溶裂隙内的水量;第五阶段(⑤)泉流量主要来源于基岩孔隙内的水量。
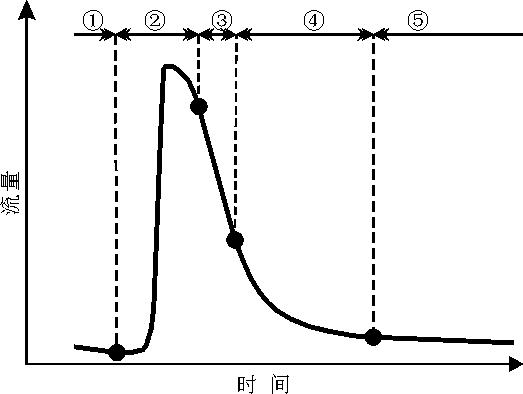 |
| 图 1 泉流量曲线 Fig.1 Hydrograph of spring discharge |
流量曲线分析理论主要研究在没有补给情况下流量的变化特征,即图1中第三、四、五阶段。第三阶段由于流量来源于岩溶管道,不符合达西定律。Kovacs等[11]使用线性方程描述这一过程,并指明流量衰减系数是管道导水性能和给水度的函数。方程为:
式中:Qt表示t时刻的泉流量(m3/d);Q0表示初始时刻的泉流量(m3/d);t表示时间(s);α1表示流量衰减系数,无量纲;Kc表示岩溶管道导水性(m3/d);f表示管道空间分布频率(1/m);Sm表示基岩给水度;A表示流域面积(m2)。
第四阶段由于没有外部补给,泉流量逐渐减少,流速很小,满足达西定律,Baedke等[12]用指数方程描述这一过程,并指明流量衰减系数是导水系数和给水度的函数。方程为:
式中:Tf表示岩溶裂隙导水系数(m2/d);Sf表示岩溶裂隙给水度,无量纲;L表示距离(m);α2表示流量衰减系数。
第五阶段泉流量来源于基岩孔隙内的水量,Dewandel等[5]用双曲线方程更加精确地描述了这一过程:
式中:Tm表示基岩导水系数;α3表示流量衰减系数。
2 研究区概况研究区位于桂林市灵川县寨底地下河流域内,是西南典型岩溶流域之一。流域面积约31.05 km2,多年平均降水量为1 601.1 mm,年平均气温为17.5 ℃。地表溪沟和地下管道非常发育,大部分区域属于峰丛洼地,地形高程260~820 m。根据含水介质特征,寨底地下河系统分为孔隙水、裂隙水和岩溶地下水。岩溶区面积 32.5 km2,其中碎屑岩区面积3.53 km2。汇水区域所包围的东村组(D3d)、桂林组(D3g)、塘家湾组(D2t)等岩溶区岩性为灰岩、白云质灰岩或白云岩,构成一个岩溶含水系统,其间未发现存在一定厚度的隔水岩层或相对隔水层。寨底地下河出口G047为唯一总排泄口(图2)。
 |
| 图 2 寨底水文地质图 Fig.2 Hydrogeological map of ZhaiDi basin |
为获取G047地下河出口流量衰减曲线,在距离出口100 m处修建薄壁堰,使用Mini Diver自动水位计分别监测薄壁堰上下游水位变化,1 h监测一次,并利用水力学公式计算地下河日流量变化。自2013年1月15日24:00至2014年1月15日24:00连续获取8 784组地下河流量数据,并使用LS-3雨量自动监测仪监测寨底降雨量变化。为减少流量衰减分析过程中降雨对流量衰减系数的影响,笔者选取一次特大降雨即2013年9月25日3:00暴雨后至10月13日17:00期间降雨较少的446组流量数据作为研究对象(图3)。从图3中可看出该时间段内仅10月1日有少量降雨,因此本文运用流量衰减分析理论计算寨底流域水文地质参数。
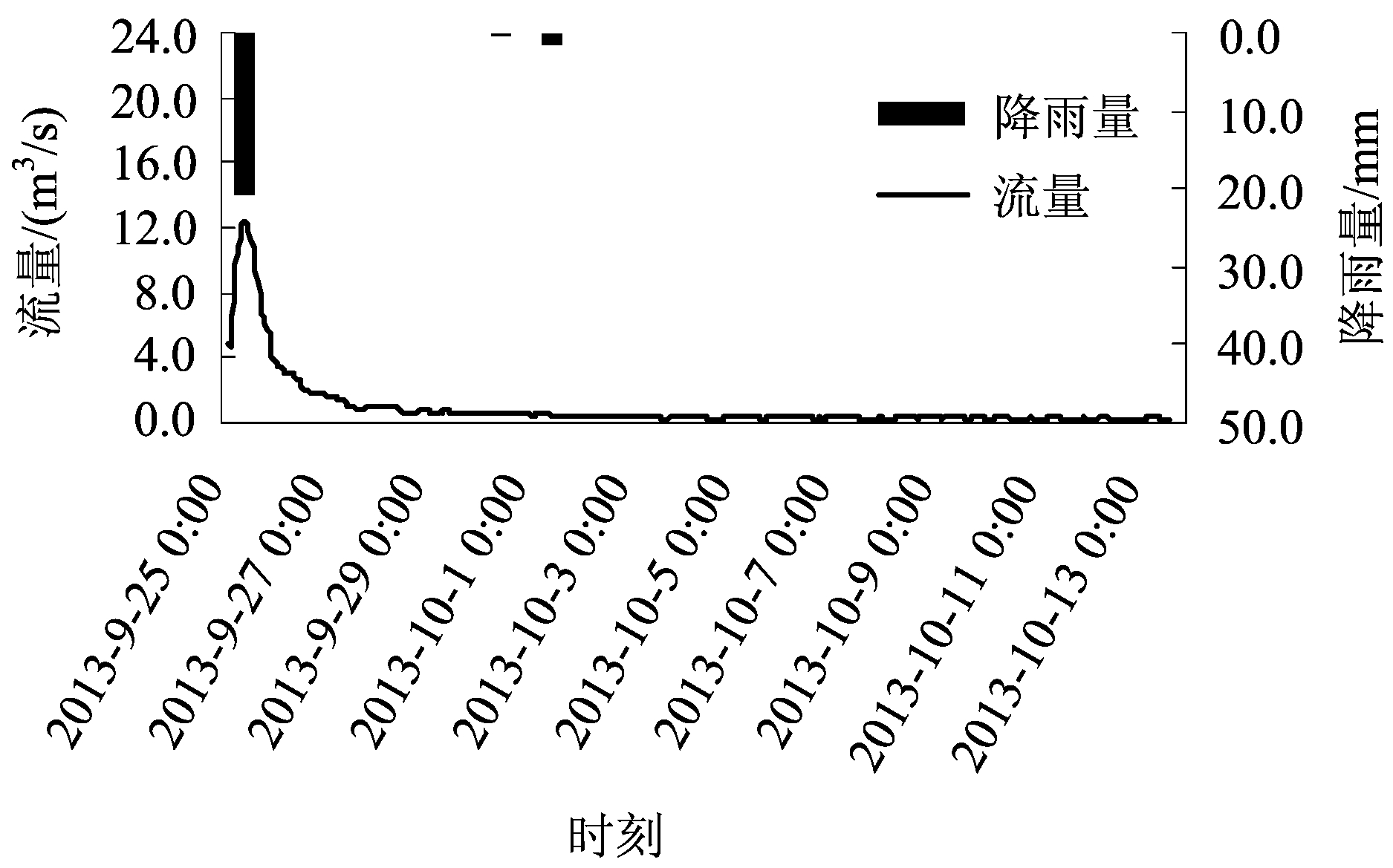 |
| 图 3 降雨量-流量曲线 Fig.3 Relationship between discharge and rainfall |
流量衰减系数是岩溶含水层参数的综合反映,通过已知方程拟合实测流量曲线,可分别确定不同阶段流量衰减系数。本文利用MATLAB对实测流量曲线分段拟合,每段拟合方程及曲线见图4。
 |
| a.第三阶段;b.第四阶段;c.第五阶段。 图 4 不同阶段曲线拟合结果 Fig.4 Flux fitting-curve for the different stages |
第四、五阶段相较第三阶段流量曲线拟合误差较大,可能原因是枯水期流量数值较小,在实际测量过程中有一定误差而波动较大。不同阶段曲线拟合结果及确定的流量衰减系数见表1,表1中R2是确定系数,越接近1.000 0表明拟合效果越好;RMSE是均方根误差,越接近0.000 0表明拟合效果越好。
| 不同阶段 | R2 | RMSE | 衰减系数 |
| 第三阶段 | 0.989 2 | 0.311 0 | 0.642 5 |
| 第四阶段 | 0.944 7 | 0.186 8 | 0.025 8 |
| 第五阶段 | 0.867 8 | 0.032 3 | 0.001 5 |
响水岩天窗至寨底出口地下河长度L约2.3 km,子系统面积A约22 697 m2,表2给出了寨底流域内子系统地下河径流距离。
| 地下河子系统 | 径流距离L/m |
| 钓岩地下河 | 1 400 |
| 琵琶塘岩溶泉 | 1 600 |
| 水牛轭地下河 | 1 150 |
| 东究地下河 | 1 050 |
| 豪猪岩地下河 | 2 350 |
| 空连山潜流 | 1 900 |
| 大坪地下河 | 1 200 |
| 响水岩地下河 | 2 300 |
| 大小浮地下河 | 1 880 |
| 总和 | 14 830 |
式(2)中管道空间分布频率f可用流域内地下河径流距离与流域总面积的比值确定。计算得知管道分布频率f为0.477 6‰,因此根据式(2)和第三阶段流量衰减系数计算得出岩溶管道导水性和基岩给水度的比值Kc/Sm为45 800 321.92 m3/d;根据式(4)和第四阶段流量衰减系数计算得出岩溶裂隙导水系数和裂隙给水度的比值Tf/Sf为55 228.31 m2/d;根据式(6)和第五阶段流量衰减系数计算得出导水系数和基岩给水度的比值Tm/Sm为3 125.89 m2/d。
为进一步确定岩溶含水层水文地质参数,使用裂隙率代替含水层给水度。因此本文通过实测裂隙宽度及线密度分布确定研究区裂隙率。岩溶裂隙发育地带,北东(NE10°)方向发育裂隙宽度为1.0 cm,线密度为7条/m,裂隙面积约0.070 m2,近似等于岩溶裂隙给水度Sf;岩溶裂隙相对较小地带,北西(NW330°NW340°)方向发育裂隙宽度约0.1 cm,线密度为13条/m,裂隙面积约0.013 m2,近似等于岩溶基岩给水度Sm。根据计算所得的比值,确定岩溶管道导水性Kc为595 404.19 m3/d,岩溶裂隙导水系数Tf为3 865.98 m2/d,岩溶基岩导水系数Tm为40.64 m2/d。岩溶管道的导水性Kc是管道几何形态的综合反映,是表征管道直径、粗糙度、长度等参数的综合函数。若假设岩溶管道横截面面积不变,则管道的导水系数Tc可用导水性能Kc与长度L的比值确定,为258.87 m2/d。
4 结语本研究选取了一次暴雨后小时流量过程作为对象,通过对比分析岩溶流量衰减的三个阶段发现不同阶段的流量衰减系数表征不同岩溶含水介质(管道介质、裂隙介质、基岩介质)的几何形态和水动力特征。流量衰减方法难点在于确定不同阶段流量拐点,需反复拟合流量衰减方程。笔者利用446组实测流量数据拟合计算不同阶段衰减系数,估算出寨底岩溶含水层不同介质的导水性能和给水度,为将来进行该流域水资源评价及水动力过程模拟提供了依据。
在实际工作中,估算流量衰减系数并结合岩溶裂隙率计算含水介质水文地质参数,相对抽水试验、注水试验等方法野外工作量少,具有可操作性,适用于缺乏水文地质参数的岩溶地区。但是由于岩溶地下河管道的复杂性和不确定性,运用流量衰减分析应注意管道分布频率和径流距离存在的误差。
| [1] | 董贵明,束龙仓,田娟,等. 西南岩溶地下河系统水流运动数值模型[J]. 吉林大学学报:地球科学版,2011, 41(4):1136-1143. Dong Guiming, Shu Longcang, Tian Juan, et al. Numerical Model of Groundwater Flow in Karst Underground River System, Southwestern China[J]. Journal of Jilin University:Earth Science Edition, 2011, 41(4): 1136-1143. |
| [2] | John J Q, David T, James A K. Modeling Complex Flow in a Karst Aquifer[J]. Sedimentary Geology, 2006, 184:343-351. |
| [3] | Schoeller H. Hydrodynamics of the Karst[J]. Hydrology of Fractured Rocks, 1965, 1: 3-20. |
| [4] | Eisenlohr L, Kiraly L, Bouzelboudjen M, et al. Numerical Simulation as a Tool for Checking the Interpretation of Karst Spring Hydrographs[J]. Hydrology, 1997, 193: 306-315. |
| [5] | Dewandel B, Lachassagne P, Bakalowicz M, et al. Evaluation of Aquifer Thickness by Analyzing Recession Hydrographs[J]. Hydrology, 2003, 274: 248-269. |
| [6] | Fiorillo F. Tank-Reservoir Drainage as a Simulation of the Recession Limb of Karst Spring Hydrographs[J]. Hydrogeology Journal, 2011, 19: 1009-1019. |
| [7] | Fiorillo F. The Recession of Spring Hydrographs, Focused on Karst Aquifers[J]. Water Resour Manage, 2014, 28: 1781-1805. |
| [8] | 林敏. 泉流量衰减方程中α系数物理意义的探讨[J]. 勘察科学技术,1984(5) :6-10. Lin Min. Discussion for the Physical Significance of Coefficient in Spring Flow Attenuation Equation[J]. Site Investigation Science and Technology, 1984 (5): 6-10. |
| [9] | 张艳芳,陈喜,程勤波,等. 基于流量衰减过程的岩溶地区水文地质参数推求方法[J]. 水电能源科学,2010, 28(11):55-58. Zhang Yanfang, Chen Xi, Cheng Qinbo, et al. Estimation of Hydrogeological Parameters for Karst Basin Based on Flux Depression Analysis[J]. Water Resources and Power, 2010, 28(11): 55-58. |
| [10] | 束龙仓,范建辉,鲁程鹏,等. 裂隙管道介质泉流域水文地质模拟实验[J]. 吉林大学学报:地球科学版,2015, 45(3): 908-917. Shu Longcang, Fan Jianhui, Lu Chengpeng, et al. Hydrogeological Simulation Test of Fissure Conduit Media in Springs Watershed[J]. Journal of Jilin University:Earth Science Edition, 2015, 45(3): 908-917. |
| [11] | Kovacs A, Perrochet P, Kiraly L, et al. A Quantitative Method for the Characterization of Karst Aquifers Based on Spring Hydrograph Analysis[J]. Journal of Hydrology, 2005, 303: 152-164. |
| [12] | Baedke S J, Krothe N C. Derivation of Effective Hydraulic Parameters of a Karst Aquifer from Discharge Hydrograph Analysis[J]. Water Resources Research, 2001, 37(1): 13-19. |