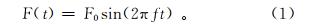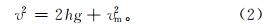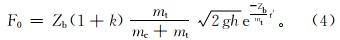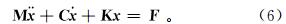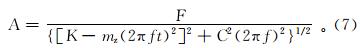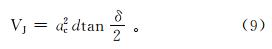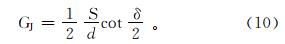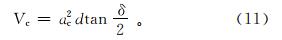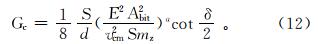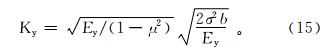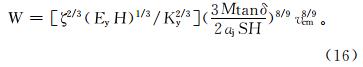2. 西南交通大学机械工程学院, 成都 610031
2. School of Mechanical Engineering, Southwest Jiaotong University, Chengdu 610031, China
0 前言
如何进行高效的破岩是石油钻探行业关注的焦点,使用高频微幅冲击振动钻具已成为当前深井、超深井钻进硬地层应用最多且效果最好的一种高效破岩技术,其在深部硬地层破岩中发挥了无可替代的优势[1, 2, 3]。
到目前为止,国内外专家学者针对冲击破岩进行了大量的研究,例如:考虑岩石疲劳损伤,利用LS-DYNA建立空气冲旋钻井钻头-岩石的互作用模型,通过仿真进行破岩的数值模拟研究[4, 5];通过破岩实验与数值模拟相结合的方法,进行单粒子的破岩分析并利用有限元建立单粒子破岩的物理模型[6, 7];针对单粒子破岩与粒子冲击钻井的真实工况存在的差异,采用无量纲化分析方法,对双粒子联合冲击破岩展开的破岩仿真研究[8];利用三牙轮钻头仿真理论,建立的冲击旋转钻井系统仿真模型[9, 10];在塔河油田进行了冲击器配合聚晶金刚石复合片(PDC)钻头提速的现场试验[11, 12, 13];根据岩石破碎的基本理论,提出的一种基于破碎比功的岩石冲击破碎效率评价方法[14]。
综上所述,现有研究主要从数值模拟、有限元仿真和现场试验入手来分析冲击破岩,并没有考虑到简谐振动激振下钻头对岩石的破岩机理的研究,也没有考虑到冲击振动作用下不同载荷频谱与岩石破碎之间的关系。因此,笔者基于以上研究岩石破碎方法的缺陷与不足,提出了考虑高频微幅冲击振动作用下岩石破碎行为计算方法,该计算方法对于提高破岩效率与进行高频微幅冲击振动破岩的理论研究具有重要的意义。研究结论可为现场的应用提供理论支撑。
1 计算分析模型高频微幅冲击振动钻具配合PDC钻头在保持旋转剪切破岩的同时,轴向冲击对岩石的破坏也起到了决定性的作用,能够实现对岩石的高频微幅纵向冲击,降低岩石抵抗破坏的能力,达到高速破岩的效果。以垂直井为例,将高频微幅冲击振动钻具进行简化,建立如图1所示的理论模型(x为横坐标,y为纵坐标,h为冲锤的行程,δ为钻头的压入角),对钻井的影响因素进行适当的简化和假设:钻头轴线与钻杆的轴线、井眼中心线等完全重合;钻杆为均质弹性直杆并忽略钻杆的弯曲和扭转变形;忽略钻杆与井眼的摩擦以及钻井液的影响等。
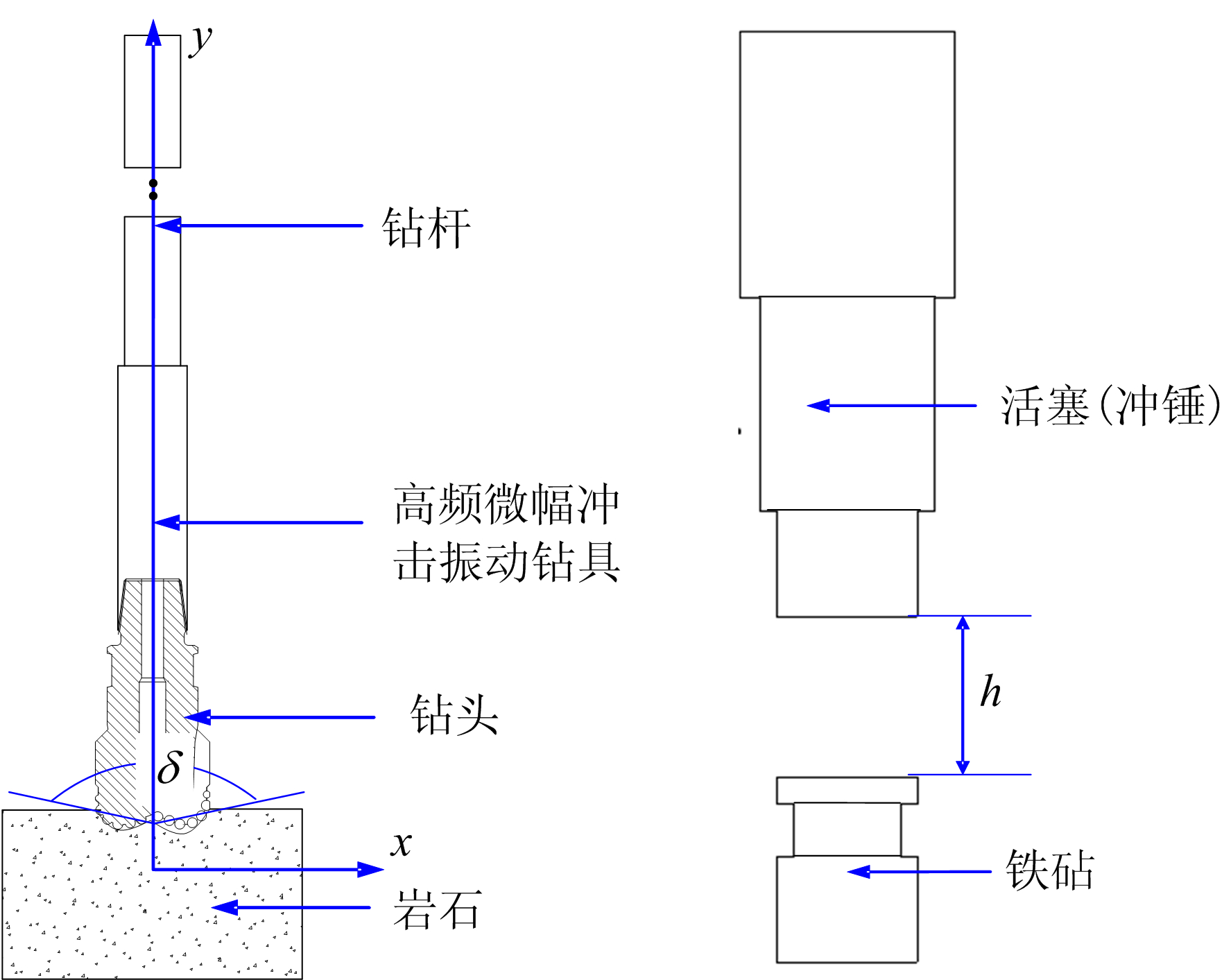 |
| 左图. 冲击模型;右图. 高频微幅冲击振动钻具简化模型。 图 1 高频微幅冲击振动模型 Fig.1 Impact vibration model of high frequency and micro amplitude |
当高频微幅冲击振动钻具和钻压推动钻头冲击岩石时,在有限的深度范围内岩石会受到一定程度上的振动响应,高频微幅冲击振动钻具向钻头传递的力为简谐力,可用如下公式表示:
式中:t为时间,s;f为冲击频率,Hz;F0为冲锤作用在铁砧面上的冲击力,N;F(t)为t时刻高频微幅冲击振动钻具输出的冲击力,N。
由经典冲击理论和自由落体运动公式可求得冲击高度与冲击速度之间的关系为
式中:v为冲锤冲击铁砧的速度,m/s;h为冲锤的行程,mm;g为重力加速度,取10 m/s2;vm为冲锤与铁砧的撞击速度,m/s,该值由感应式线速度测量法获得。
假定冲锤和铁砧的轴线是重合的,忽略高频微幅冲击振动钻具内的摩擦阻力,由经典碰撞理论可以求得冲锤冲击铁砧的实际速度vs为:
式中:k为恢复系数,由经验可取0.556;mt为铁砧的质量,kg;mc为冲锤的质量,kg。
根据力与速度、加速度之间的关系以及公式(2)、(3),可求得作用在铁砧面上的冲击力F0为:
式中:Zb为钻杆的波阻抗,Zb=ρc,ρ为钻杆的密度,g/cm3,c为钻杆的纵波传播速度,m/s; t′为冲击周期,s。
将公式(4)代入公式(1)可求得在任意时刻高频微幅冲击振动钻具所输出的冲击力为
由于钻头受到高频微幅冲击振动钻具的作用力而产生的受迫振动和作用在钻头上的钻压,使岩石受到巨大的冲击,通过离散化的方法建立整个系统的微分振动方程,可写成如下矩阵形式:
式中:M为系统的总质量矩阵;C为阻尼矩阵;K为系统的总刚度矩阵;x为节点位移向量;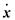 为节点速度向量;
为节点速度向量;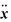 为节点加速度向量;F为整体载荷向量,包括冲击力和钻压。
为节点加速度向量;F为整体载荷向量,包括冲击力和钻压。
由公式(6)可求出在冲击载荷作用下的幅值A,即
式中:F为钻具对岩石的冲击力,N;K为钻具的刚度,N/m;mz为钻具的质量,kg; C为阻尼系数。
破岩体积和破岩比功是衡量岩石破碎效率的两个重要指标,如何准确的求出这两个指标是进行钻头破岩分析的前提和基础。钻头吃入岩石时,其抗吃入系数S(单位吃入岩石所需要的载荷)为:
式中,ac为吃入深度,mm。
在静载(钻压)作用下岩石破碎的破碎体积VJ为
式中,d为复合片的直径,mm。
岩石的破碎比功GJ为:
当高频微幅冲击振动钻具对钻头产生强烈的冲击时,随着冲击频率和幅值的变化,岩石的损伤和破坏程度也在发生着变化。在高频微幅冲击作用下岩石的破碎体积Vc的计算公式与VJ相同,即
根据波动凿入理论和公式(6)求得的钻头在冲击作用下对岩石产生的吃入深度、冲击末速度,可求得在冲击作用下岩石的破碎比功Gc为:
式中:E为钢材的弹性模量,MPa;Abit为钻头的横截面面积,mm2;vcm为冲击末速度,m/s;a=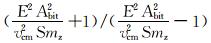 。
。
在断裂力学中,岩石的单位面积上的表面能γ(MPa·μm)的计算是极其复杂的,通常采用试验或查表的方式获得。但根据断裂力学中固体的强度理论知识也可求得,即
式中:σ为岩石的断裂强度,MPa;b为岩石原子间的间距,μm;Ey为岩石的弹性模量,MPa。
由经典的Griffith能量理论可求得岩石裂纹扩展的断裂能Lw为:
将公式(13)、(14)代入断裂能与断裂韧性的关系公式可得:
式中:μ为岩石的泊松比;Ky为岩石的断裂韧性,MPa·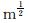 。
。
式中:ζ为与岩石性质和钻头形状无关的无量纲量,常取值为1×103~5×103;H为岩石的硬度(莫氏硬度),MPa;aj为钻头的直径,mm。
2 算例分析根据建立的计算方法进行算例分析。利用给定的参数,进行高频微幅冲击振动作用下冲击时间、冲击频率、冲击力的计算和分析。本文选用典型的阀式正作用液动冲击器,选取特定的冲击频率,研究在不同的冲击频率下PDC钻头对岩石的吃入深度、冲击末速度产生的影响,以及不同的冲击频率、幅值对岩石的破岩体积、破岩比功的求解和分析;将计算结果与静载下求得的破岩体积和破岩比功的计算结果进行对比分析;然后在假定频谱一定的条件下,研究不同的岩石性能参数与裂纹长度的关系。算例参数如表1所示。为了验证计算方法的准确性与可靠性,利用实验参数代入计算方法进行求解与分析。
| 参数名称 | 结果 |
| 钻杆的长度/m | 10 |
| 钻杆的内径/mm | 112 |
| 钻杆的外径/mm | 127 |
| 钻杆的纵波传播速度/(m/s) | 1 000 |
| 钻杆的密度/(g/cm3) | 7.85 |
| 钻压/kN | 10 |
| 冲锤的行程/cm | 15 |
| 冲锤的质量/kg | 35 |
| 铁砧的质量/kg | 25 |
| 冲击振动钻具的刚度/(N·m) | 150×106 |
| 冲击振动钻具的质量/kg | 100 |
| 钢材的弹性模量/MPa | 210×103 |
| 钻头的直径/mm | 152 |
| 复合片的直径/mm | 14 |
| 钻头的压入角/rad | 2.094 |
| 钻头的质量/kg | 24.5 |
| 阻尼系数 | 0.1 |
根据理论分析、计算方法和算例参数,可求得冲击时间与冲击频率、冲击频率与冲击力的关系曲线,如图2、图3所示。
 |
| 图 2 冲击时间与冲击频率关系曲线 Fig.2 Relation curve between the impact time and impact frequency |
 |
| 图 3 冲击力与冲击频率关系曲线 Fig.3 Relation curve between the impact force and impact frequency |
由图2、图3可以看出:随着冲击频率的增加,冲击时间的周期在不断减小,而冲击力却在显著地增加,在高频微幅振动冲击中,冲击时间与冲击频率呈反比的关系,冲击频率与冲击力呈正比的关系。
根据图3中的计算结果选取特定的点以及上述计算方法对其进行分析,可得到在不同的冲击频率下,PDC钻头对岩石的吃入深度、冲击末速度所产生的影响,见图4、图5;然后将所得时域图向频谱图转化,进行频谱分析,如图6、图7所示。
 |
| 图 4 不同频率下吃入深度时域图 Fig.4 Time domain chart of bit penetration under different frequency |
 |
| 图 5 不同频率下冲击末速度时域图 Fig.5 Time domain chart of final impact velocity under different frequency |
 |
| 图 6 不同冲击力对应的吃入深度下的频谱图 Fig.6 Frequency spectrogram of bit penetration under different impact forces |
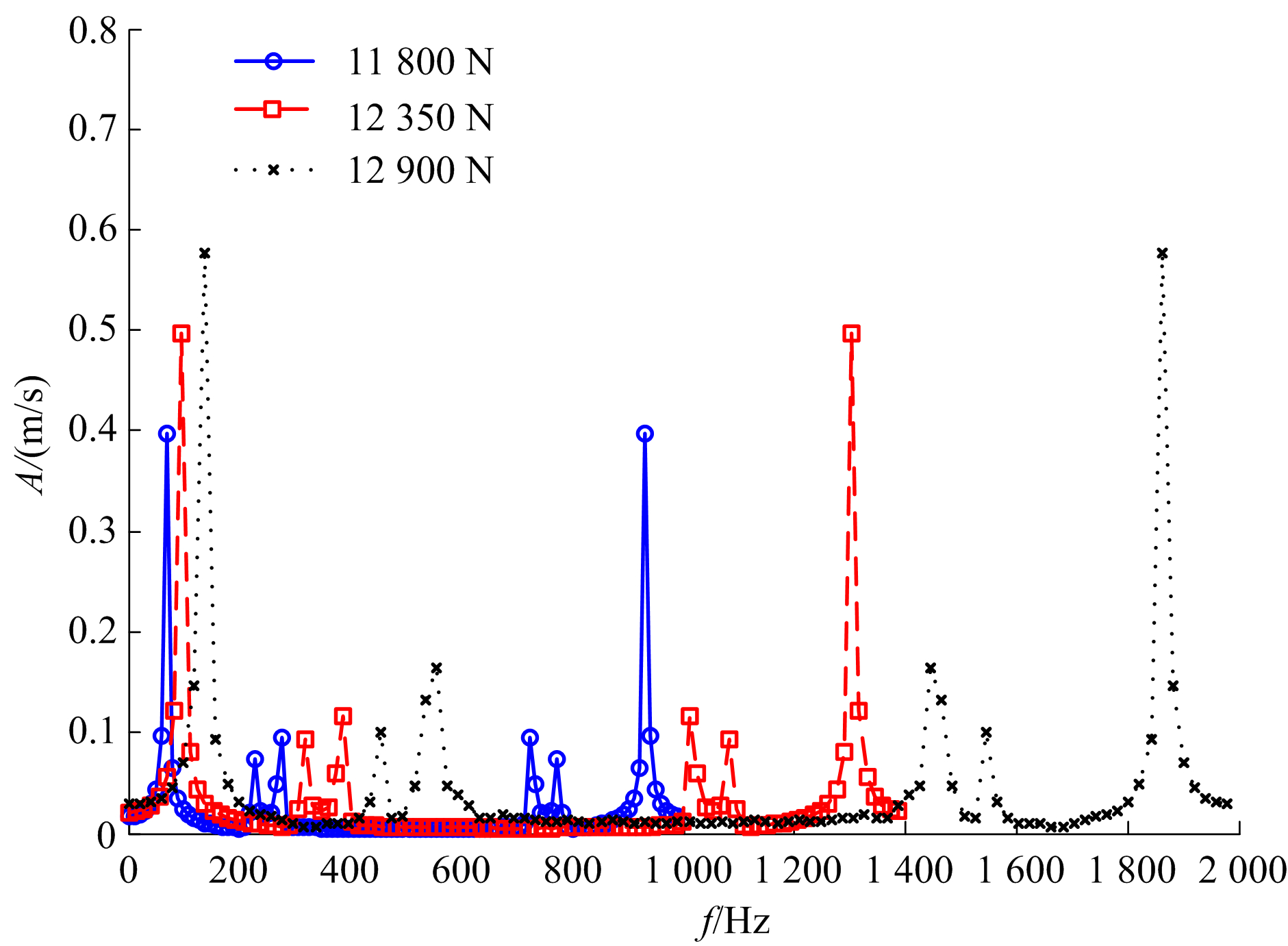 |
| 图 7 不同冲击力对应的冲击末速度下的频谱图 Fig.7 Frequency spectrogram of final impact velocity under different impact forces |
由图4、图5可知:在高频微幅冲击振动钻进过程中,PDC钻头对岩石的吃入深度、冲击末速度与冲击频率有着密切的关系,随着冲击频率的增加,PDC钻头吃入岩石的深度以及对岩石产生的冲击末速度也在增加。由图6、图7的频谱图可以看出,在高频冲击的情况下幅值都比较小(不超过0.6m/s),并且幅值的变化规律大多都以冲击频率为中心呈对称分布。
破岩体积、破岩比功是衡量破岩效率的重要指标。根据计算方法以及上述的计算结果,对破岩效率进行求解和分析,在计算分析中,关于岩石的参数仍然采用试验中所用岩石参数,具体参数如表2所示。
| 参数名称 | 结果 |
| 灰岩弹性模量/MPa | 31.2×103 |
| 灰岩单位面积上的表面能/(MPa·μm) | 0.067 66 |
| 砂岩1号弹性模量/MPa | 11.54×103 |
| 砂岩1号单位面积上的表面能/(MPa·μm) | 0.030 24 |
| 砂岩2号弹性模量/MPa | 5.22×103 |
| 砂岩2号单位面积上的表面能/(MPa·μm) | 0.017 65 |
根据动静载荷的破岩体积、破岩比功计算公式(8)-(12)和具体参数,可求得在静载(钻压)、不同冲击频率下压入角与破岩体积、破岩比功的关系,如图8、图9所示。
 |
| 图 8 动、静载荷的破岩体积图 Fig.8 Rock-breaking volume under dynamic and static loads |
 |
| 图 9 动、静载荷的破岩比功图 Fig.9 Rock-breaking work ratio under dynamic and static loads |
由图8、图9可以看出,随着压入角的增加,破岩体积也在增加,而破岩比功却在减小。当压入角为一定值时:在高频微幅冲击振动作用下对岩石的破岩体积要高于静载条件下对岩石的破岩体积,随着冲击频率的增加,岩石的破岩体积也在增加;但在静载(钻压)的作用下对岩石产生的破岩比功要明显高于高频微幅冲击下对岩石的破岩比功,随着冲击频率的增加,破岩比功在不断地减小。即:在高频微幅冲击振动作用下,冲击频率越高,破岩体积越大,破岩比功越小;与静载相比,动载的破岩体积大、破岩比功小,有利于提高破岩效率。利用岩石裂纹长度计算公式和具体参数,选定冲击频率为2 000 Hz以及在特定的岩石弹性模量下,计算和分析不同的岩石硬度、泊松比对岩石裂纹长度的影响,结果如图10所示。
由图10可以看出:一定的冲击频率、幅值条件下,随着弹性模量、泊松比、岩石硬度的增加,岩石的裂纹长度在不断减小;当岩石的弹性模量为5.22 GPa、泊松比为0.10、岩石的硬度100 MPa时,岩石的裂纹长度达到最大值,破岩效率达到最佳状态。
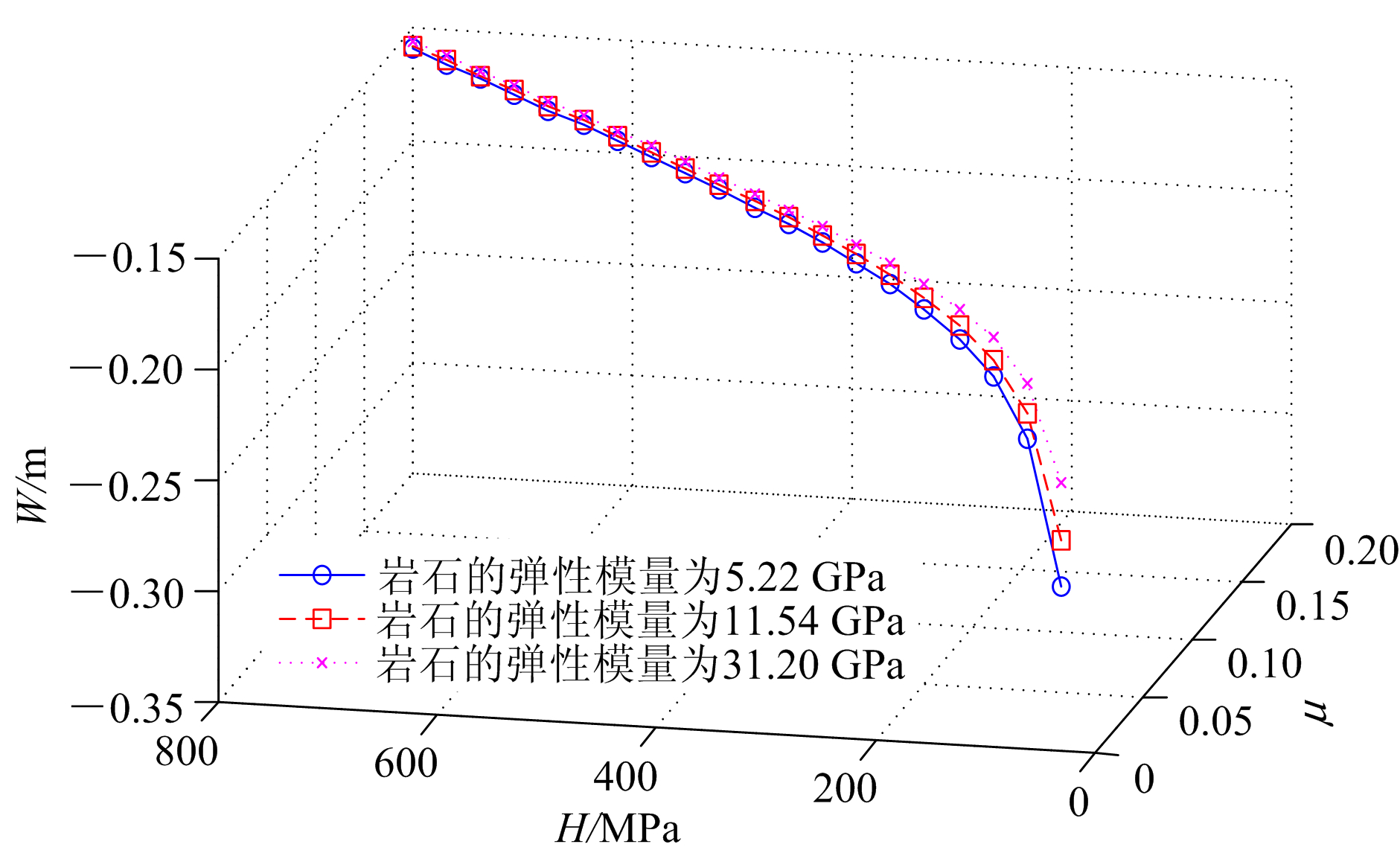 |
| W的负号代表反方向。μ为泊松比。 图 10 不同的岩石性能对中间、径向裂纹长度的影响 Fig.10 Effects of different rock properties on middle and radial crack length |
为了验证计算方法的准确性,进行试验测试与结果分析。采用算例中的参数进行试验设计,包括冲击时间、冲击频率、冲击力、破岩效率测试等内容。试验的岩石材料主要有灰岩、砂岩2号,具体参数如表3所示。试验设备主要为动静组合载荷岩石破碎多功能试验机、声发射检测系统、高清晰度的摄像机等。首先,针对算例中的冲击参数,模拟高频微幅冲击振动测试系统,利用动静组合载荷岩石破碎多功能试验机进行冲击时间、冲击力的测试,然后配合声发射检测系统进行连续检测并获得冲击时间,测试结果如图11所示。采用高速摄像仪摄录不同岩石在静载和受不同冲击频率下的岩石破碎情况、部分岩石裂纹扩展情况,以及当冲击频率一定时不同岩石的岩石裂纹扩展情况,并进行对比分析。测试结果如图12a、b、c所示,根据测试结果进行不同岩性破岩效率的对比分析,如图12d所示。
| 岩石 | 灰岩 | 砂岩2号 |
| 单轴抗压强度/MPa | 105.951 | 50.565 |
| 弹性模量/GPa | 31.20 | 5.22 |
| 泊松比 | 0.171 | 0.111 |
| 抗拉强度/MPa | 6.758 | 2.836 |
| 抗剪强度/MPa | 17.72 | 11.69 |
| 内摩擦角/rad | 0.76 | 0.60 |
| 硬度/MPa | 1 523.6 | 541.3 |
| 塑性系数 | 1.32 | 4.09 |
| PDC钻头可钻性级值 | 7.01 | 3.05 |
| 钻头的压入角/rad | 2.094 | 2.094 |
| 岩石的抗吃入系数 | 8 690 | 4 320 |
| 复合片的直径/mm | 14 | 14 |
| 钻头的横截面面积/m2 | 146×10-3 | 146×10-3 |
| 冲击末速度/(m/s) | 0.58 | 0.58 |
| 钢材的弹性模量/MPa | 210×106 | 210×106 |
| 试验系统的总质量/kg | 125 | 125 |
 |
| 图 11 冲击频率的测试结果 Fig.11 Test results of impact frequoncy-time,force-time and force-frequency |
 |
| a. 破岩效率的测试结果;b.灰岩的岩石裂纹扩展情况;c. 冲击频率为2 000 Hz时不同岩石的裂纹扩展情况;d. 同一频率下不同岩石的破岩效率对比。 图 12 试验结果 Fig.12 Test results |
对试验过程中测得的冲击时间、冲击频率、冲击力的精确度与关系进行分析,结果与算例中的基本吻合,试验测试数据与理论计算数据误差在5%以内,并且随着冲击时间的增加,冲击力与冲击频率都在减小。通过改变试验参数,对比不同的测试结果可知:与静载相比,高频微幅冲击振动对岩石的破碎效果更明显,并且随着冲击频率和幅值的变化,破岩体积、破岩比功、破岩效率也在发生着变化。对于砂岩2号:当冲击频率为2 000 Hz时的破岩体积为213.4 mm3,破岩比功为3.12 kJ·m-4;当为静载作用时的破岩体积为92.3 mm3,破岩比功为7.2 kJ·m-4。即冲击频率为2 000 Hz的破岩体积大约是静载时的2.3倍。对于灰岩:冲击频率为2 000 Hz时的破岩体积为121.6 mm3,破岩比功为6.3 kJ·m-4;当为静载作用时的破岩体积为65.37 mm3,破岩比功为11.4 kJ·m-4。即冲击频率为2 000 Hz的破岩体积大约是静载时的1.86倍。岩石的裂纹长度也与冲击频率的大小有着密切的关系。当岩性相同时,随着冲击频率的增加,岩石的裂纹长度也在不断地增加(图12b)。岩石的破坏形式为剪切破坏,岩石的裂纹扩展总是沿着45°方向进行发展;当冲击频率(频谱)为定值时,岩石的裂纹长度也与弹性模量、泊松比、岩石硬度有着密切的关系。当冲击频率为2 000 Hz时,砂岩2号的岩石裂纹长度远大于灰岩,并且砂岩2号已经发生了断裂(图12c)。在一定的冲击频率下,随着弹性模量、泊松比、岩石硬度、可钻性等参数的变化,不同岩石的破岩效率也在发生变化,图12d中砂岩2号的上述岩性参数要明显低于灰岩,而对砂岩2号的破岩效率明显高于灰岩的破岩效率。
4 结论1)根据现有岩石破碎研究的现状与不足,提出了一种新的岩石破碎计算方法,建立了高频微幅冲击振动模型,分析冲击频率、冲击时间、冲击力等参数的关系,并据此建立了破岩体积、破岩比功、破岩裂纹长度的计算模型。
2)与静载相比,高频微幅冲击振动对岩石的破碎效果更明显,破岩体积更大,岩石的裂纹更长,但破岩比功更小。
3)随着冲击频率和幅值的变化,破岩体积、破岩比功、破岩效率也在发生着变化,当冲击频率和幅值增加时,破岩体积不断增加,但破岩比功不断减小。
4)岩石的裂纹长度不仅与冲击频率的大小有关,而且与岩石的弹性模量、泊松比、硬度有密切的关系,随着弹性模量、泊松比、岩石硬度的增加,岩石的裂纹长度不断减小。
5)实际钻井过程中,不仅存在着纵向冲击振动,还存在着扭转振动和横向振动,而这些振动都会影响着岩石的破碎效果,对于纵向、横向、扭转振动之间的耦合对岩石破碎效果的影响有待进一步的深入研究。
| [1] | Li Zifeng. Criteria for Jet Cavitation and Cavitation Jet Drilling[J]. International Journal of Rock Mechanics & Mining Sciences, 2014, 71: 204-207. |
| [2] | Barani A, Amini S, Paktinat H, et al. Built-Up Edge Investigation in Vibration Drilling of Al2024-T6[J]. Ultrasonics, 2014, 54: 1300-1310. |
| [3] | Aron D, Ryan W, Abhijeet N, et al. Application of a Torsional Impact Hammer to Improve Drilling Efficiency[C]//Society of Petroleum Engineers. SPE Annual Technical Conference and Exhibition. Denver: SPE, 2011:1-11. |
| [4] | 殷其雷, 殷琨, 柳鹤, 等. 潜孔锤反循环钻进技术在某水电站的试验应用[J]. 吉林大学学报:地球科学版, 2014, 44 (3): 961-968. Yin Qilei, Yin Kun, Liu He, et al. Application Test of DTH Hammer Reverse Circulation Drilling Technique in a Hydropower Station[J]. Journal of Jilin University: Earth Science Edition, 2014, 44(3): 961-968. |
| [5] | 况雨春, 朱志谱, 蒋海军, 等. 单粒子冲击破岩实验与数值模拟[J].石油学报, 2012, 33(6): 1059-1063. Kuang Yuchun, Zhu Zhipu, Jiang Haijun, et al. Experimental Study and Numerical Simulation of Single-Particle Impacting Rock[J]. Acta Petrolei Sinica, 2012, 33(6):1059-1063. |
| [6] | Zhu Haiyan, Deng Jingen, Xie Yuhong, et al. Rock Mechanics Characteristic of Complex Formation and Faster Drilling Techniques in Western South China Sea Oilfields[J]. Ocean Engineering, 2012, 44:33-45. |
| [7] | 伍开松, 荣明, 李德龙, 等. 双粒子联合冲击破岩仿真研究[J]. 岩土力学,2009, 30(增刊1): 19-23. Wu Kaisong, Rong Ming, Li Delong, et al. Simulation Study of Impacting Breaking Rock by Double Particle[J]. Rock and Soil Mechanics, 2009, 30(Sup.1):19-23. |
| [8] | 石旭飞, 张文静, 王寒梅, 等. 人工回灌过程中的水-岩相互作用模拟[J]. 吉林大学学报: 地球科学版, 2013, 43 (1): 220-227. Shi Xufei, Zhang Wenjing, Wang Hanmei, et al. Modeling of Water-Rock Interaction During the Artificial Recharge[J]. Journal of Jilin University: Earth Science Edition, 2013, 43 (1): 220-227. |
| [9] | 朱海燕, 刘清友, 邓金根, 等. 冲旋钻井条件下的岩石破碎机理[J]. 应用基础与工程科学学报, 2012, 20(4): 622-630. Zhu Haiyan, Liu Qingyou, Deng Jingen, et al. Rock-Breaking Mechanism of Rotary-Percussive Drilling[J].Journal of Basic Science and Engineering, 2010, 20(4):622-630. |
| [10] | Tan Songcheng, Fang Xiaohong, Yang Kaihua, et al.A New Composite Impregnated Diamond Bit for Extra-Hard, Compact, and Nonabrasive Rock Formation[J].Journal of Refractory Metals and Hard Materials, 2014, 43:186-192. |
| [11] | Liu Songyong, Liu Zenghui, Cui Xinxia, et al. Rock Breaking of Conical Cutter with Assistance of Front and Rear Water Jet[J]. Tunnelling and Underground Space Technology, 2014, 42:78-86. |
| [12] | 李广国, 索忠伟, 王金荣, 等. 塔河油田液动射流冲击器+PDC钻头提速技术[J]. 石油钻探技术, 2013, 41(5): 71-75. Li Guangguo, Suo Zhongwei, Wang Jinrong, et al. Improve ROP with Hydraulic Percussion Hammer and PDC Bit in Tahe Oilfield[J].Petroleum Drilling Techniques, 2013, 41(5):71-75. |
| [13] | 孙友宏, 高科, 张丽君, 等. 耦合仿生孕镶金刚石钻头高效耐磨机理[J]. 吉林大学学报:地球科学版, 2012, 42(增刊3): 220-225. Sun Youhong, Gao Ke, Zhang Lijun, et al. High Drilling Efficiency and Wear-Resistant Mechanism of Coupling Bionics Impregnated Diamond Bit[J]. Journal of Jilin University: Earth Science Edition, 2012, 42(Sup.3):220-225. |
| [14] | 闫铁, 李玮, 毕雪亮, 等.一种基于破碎比功的岩石破碎效率评价新方法[J]. 石油学报, 2009, 30(2): 291-294. Yan Tie, Li Wei, Bi Xueliang, et al. A New Evaluation Method for Rock-Crushing Efficiency Based on Crushing Work Ratio[J]. Acta Petrolei Sinica, 2009, 30(2):291-294. |
| [15] | Lu Yiyu, Tang Jiren, Ge Zhaolong, et al. Hard Rock Drilling Technique with Abrasive Water Jet Assistance[J]. International Journal of Rock Mechanics & Mining Sciences, 2013, 60: 47-56. |