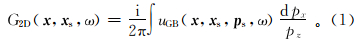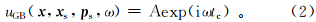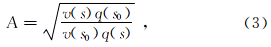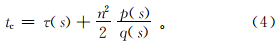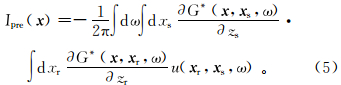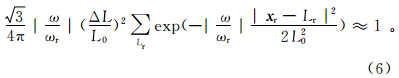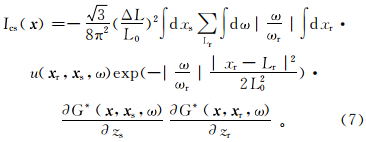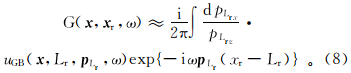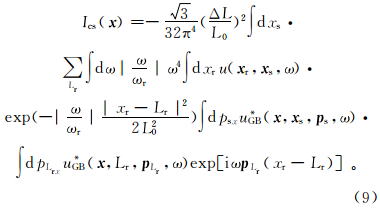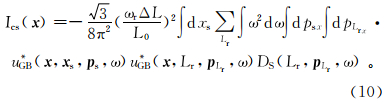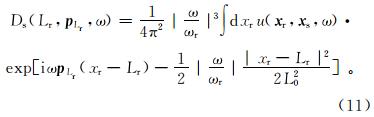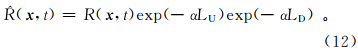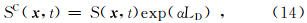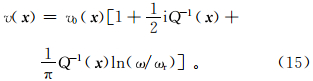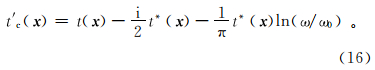2. 中国石油大学(北京)海洋石油勘探国家工程实验室, 北京 102249
2. National Engineering Laboratory for Offshore Oil Exploration, China University of Petroleum, Beijing 102249, China
0 引言
地下介质的黏滞性造成地震波的振幅衰减和相位畸变,尤其是在气云这样的高衰减区。对这类数据偏移时,气云和它下方的构造不能很好地成像[1]。为了提高偏移成像分辨率,需要补偿这类衰减效应。
早期的吸收补偿是对地震道做反Q(品质因子)滤波[2, 3, 4],但是其基于一维波动方程对地震记录逐道补偿,不能适应复杂构造。实际上,Q值是空间变化的,吸收衰减对地震信号的影响与波的传播路径有关[5]。所以,理想的补偿方法应该根据其实际传播路径,在偏移成像的过程中进行[6]。过去的二十几年中,有许多学者利用频率域的单程波方程补偿上、下行波的衰减和频散效应[7, 8, 9, 10]。概括来说,这些方法通常是把衰减表示为复相速度的虚部,因此可以灵活处理任意衰减模型。
基于波动方程偏移的衰减补偿能对复杂构造进行更准确的成像,但是计算效率较低。Kirchhoff偏移在补偿衰减的过程中不需要输出每一个CIG(共成像点)道集,计算速度快,不足的地方是存在多值走时问题。高斯束偏移[11, 12, 13, 14, 15, 16, 17]是近年来发展的一种优秀的偏移算法,不仅具有接近于波动方程偏移的成像精度,而且保留了Kirchhoff 积分法高效灵活的优点,能够有效处理多初至。
本文在高斯束偏移的基础上,研究基于吸收衰减补偿的高斯束叠前深度偏移。首先给出共炮域高斯束叠前深度偏移原理;然后推导补偿吸收衰减的表达式,校正Q引起的振幅衰减和相位畸变,实现衰减补偿的高斯束叠前深度偏移;最后用数值算例证明该方法的有效性和优越性。
1 方法原理高斯束方法的核心是格林函数的合成。利用格林函数可以得到地震波场,描述地震波的传播过程。因此,这里首先介绍格林函数的合成方法,然后直接给出由格林函数表示的共炮道集高斯束叠前深度偏移公式。
1.1 高斯束积分表示的格林函数在高斯束方法中,二维格林函数G2D( x,x s,ω)是通过一系列由源点出射的具有不同出射角θ的高斯束叠加积分表示的[18]。其中:ω是圆频率; x =(x,z)和 x s=(xs,zs)是地下任意一点和震源点的坐标,如图 1所示。
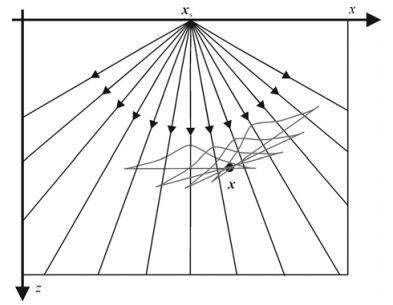 |
| 图 1 格林函数的高斯束叠加合成 Fig.1 Green function in terms of Gaussian beams summation |
从源点 x s处以不同的角度出射中心射线束,每条中心束附近波场值用高斯束方法求取。地下介质中 x 点的波场值由与其临近的多条高斯束叠加而得,则高斯束表示的格林函数公式为[12, 16]
式中: p s=( px,pz)为中心射线的参数矢量,px和pz 分别表示射线参数的水平分量和垂直分量;uGB( x,x s,p s,ω) 为高斯束方法求取的波场位移,
式中,A,t c分别是高斯束的复值振幅和复值旅行时,且 式中:s0是射线追踪的起点;s是射线路径;v(s)是沿射线的速度;τ(s)是沿着射线的旅行时;p(s)和q(s)是动力学射线追踪方程组的复值解[18],它们决定了高斯束的能量分布;n表示沿射线法线方向的距离。高斯束构建的格林函数由多条中心射线附近有限区域的局部波场叠加得到,利用不同的波束叠加可以解决多值走时问题。采用Hill[11]给定的初始值求解动力学射线追踪方程组,可以保证高斯束是正则的,因而由高斯束所表示的格林函数也是处处正则的,避免了复杂构造下的焦散问题。
1.2 共炮集高斯束叠前深度偏移高斯束叠前偏移由上行波场和下行波场的互相关得到,原理如图 2所示。在震源和束中心处分别以不同的射线参数 p s和 p L r出射高斯束进行波场计算。其中: s表示震源位置;Lr表示束中心位置。
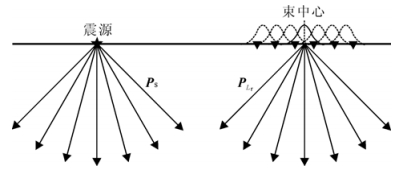 |
| 图 2 共炮道集高斯束叠前深度偏移原理图 Fig.2 Sketch of common shot Gaussian beam prestack depth migration |
利用高斯束积分表征的格林函数来描述上、下行波场,则共炮道集高斯束叠前成像公式[19]为
式中: u( x r,x s,ω)是记录波场; x s=(xs,zs)表示震源坐标,x r=( x r,z r)表示检波点坐标;G*是格林函数的共轭,其对z的偏导数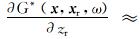 -iωpLrzG*( x,x r,ω) ; I pre( x )为最终的叠前成像值。
-iωpLrzG*( x,x r,ω) ; I pre( x )为最终的叠前成像值。
高斯函数具有如下性质:
式中:ωr为参考频率;ΔL为束中心间隔;L0表示ωr下的初始束宽[11, 13]。将式(6)代入式(5),得到 式中: I cs(x)表示 x 点的共炮偏移成像值;震源格林函数 G( x,x s,ω )用式(1)表示;束中心Lr有效范围内接收点的格林函数 G( x,x r,ω )用下式表示:将这两个格林函数分别代入式(7)可得
式(9)进一步简化为
式(10)即为最终的叠前共炮点道集高斯束偏移公式。其中: p Lr=(pLrx,pLrz)是接收点射线参数;Ds(Lr,p Lr,ω) 为地震记录的加窗局部倾斜叠加。
1.3 衰减介质共炮集高斯束叠前深度偏移图 3为衰减介质中的正演与偏移示意图。图 3a中,由于品质因子Q的存在,波从震源到反射点、再到检波点,沿整个传播路径的累积衰减量为exp(-αLU)exp(-αLD)(α是衰减系数,LU和LD分别为上行波和下行波的传播距离),则衰减后的检波点波场为
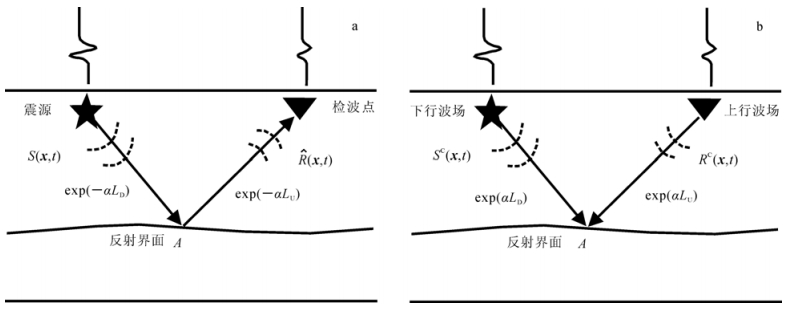 |
| a. 正演;b. 偏移。S(x,t)为参考震源波场;R(x,t)为参考检波点波场(即无衰减地震波场)。 图 3 衰减介质中的正演与偏移示意图 Fig.3 Schematic of forward modeling and migration in an attenuating medium |
为了实现对检波点波场的完全补偿,检波点的校正量应该为exp(αLU)exp(αLD)。然而在互相关成像中,传播距离为LU(检波点到反射点)的检波点补偿算子为exp(αLU),补偿后的检波点波场为
因此,还需要同时补偿下行(震源)波场。沿着射线路径、传播距离为LD(震源到反射点)的震源补偿算子为exp(αLD),补偿后的震源波场为
如图 3b所示。这样补偿后的互相关成像剖面才能达到与参考偏移剖面相当的效果。
波在黏声波介质中传播可认为是复速度的波在声波介质中传播,复速度的实部是声波介质中的速度 ,品质因子Q代表衰减。如果衰减小(1/Q≤1),则复速度可以表示为[20, 21]
其中:Q不依赖于频率;速度的虚部引起沿射线路径的指数衰减;速度的实部包含频散项,确保波动方程解的因果性。当1/Q≤1时,对于一阶项,射线路径保持不变。因此,衰减只通过依赖于频率的复值旅行时影响波形。复值旅行时为
式中: t( x )是声波介质中的旅行时; t*( x )= ,ray表示沿射线积分。
,ray表示沿射线积分。
用式(16)的t′c( x )替换式(4)中的tc( x ),再将得到的格林函数代入叠前偏移公式,即可得到衰减介质中的高斯束偏移公式。
2 模型算例分析 2.1 两层模型笔者设计了简单的两层模型。模型大小为3 000 m×3 000 m,如图 4所示。震源采用主频为20 Hz的Ricker子波,坐标为(1 500 m,0 m),共设计了301个检波点,布置在地表0~ 3 000 m处,道间距为10 m,接收记录长度为2 s,时间采样间隔是0.001 s。
 |
| 图 4 两层介质速度和Q值模型 Fig.4 Two layer model with velocity and Q values |
为了更直观地反映衰减和补偿过程,将分别输出界面附近某一时刻的参考、未补偿和补偿后的震源、检波点波场快照以及互相关成像剖面。震源波场由点源出射的高斯束正向延拓得到;检波点波场由检波点处束中心局部倾斜叠加后的平面波反向外推得到;互相关成像剖面为单炮偏移结果。如图 5,6和7所示,炮点位于(1 500 m,0 m),图中虚线为界面位置(深度1 500 m)。
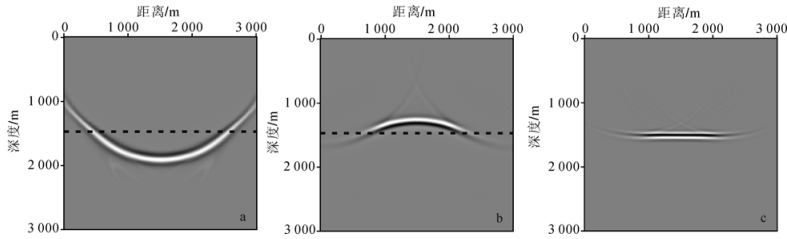 |
| a. 震源波场;b. 检波点波场;c. 互相关结果。 图 5 参考的震源、检波点波场以及互相关成像剖面 Fig.5 Reference source wavefield, receiver wavefield and cross-correlation results |
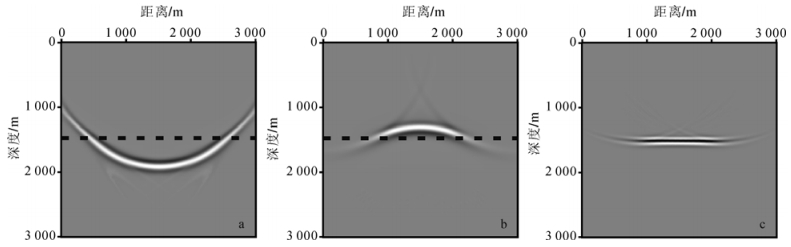 |
| a. 震源波场;b. 检波点波场;c. 互相关结果。 图 6 未补偿的震源、检波点波场以及互相关成像剖面 Fig.6 Noncompensated source wavefield, receiver wavefield and cross-correlation results |
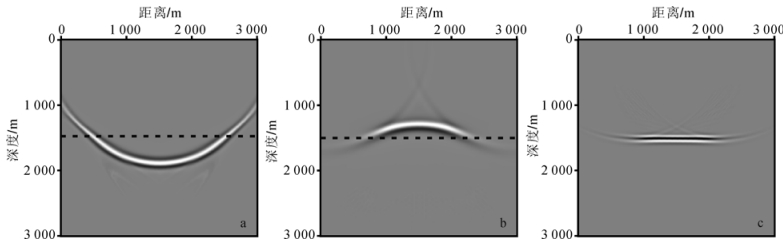 |
| a. 震源波场;b. 检波点波场;c. 互相关结果。 图 7 补偿后的震源、检波点波场以及互相关成像剖面 Fig.7 Compensated source wavefield, receiver wavefield and cross-correlation results |
图 5为参考波场,没有考虑吸收衰减。图 6是未补偿的波场:图 6a与图 5a相同;6b是检波点波场,其输入为黏声波地震记录,与参考波场图 5b相比,存在明显的振幅衰减和相位畸变(能量较弱,同一时刻的波场位置下移)。图 7是补偿后的结果:与未补偿的(图 6)相比,补偿后的震源(图 7a)和检波点波场(图 7b)振幅均得到加强,相位得到校正(位置上移,图 7b、c恢复到图 5b、c的位置)。对比互相关结果(图 5c,图 6c,图 7c)可以看出,本文方法在偏移过程中有效地补偿了地震记录的能量衰减,补偿后的成像效果(图 7c)与参考结果(图 5c)相当。
图 8是从图 5c,6c和7c中抽取的单道记录对比结果。从图 8中也可以看出,黏声波高斯束叠前深度偏移有效地补偿了地下介质对地震波的吸收。
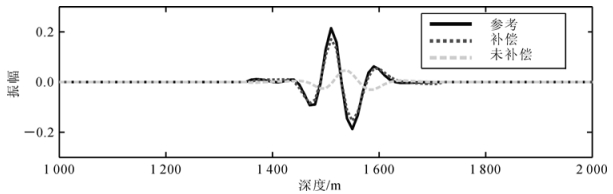 |
| 图 8 从成像剖面(图5c,6c和7c)中抽出的单道波形对比(水平距离1 500 m处) Fig.8 Comparison of the single trace waveforms (at lateral distance 1 500 m) extracted from image results (Figure 5c, 6c and 7c) |
在第二个例子中,我们考虑实际的衰减模型。图 9是气云速度模型和相应的Q模型(BP模型的一部分[22])。模型的顶部偏中是由于气云的存在导致的低速和高衰减区。模型网格数为398×161,网格大小是10 m×10 m。共40炮,震源采用主频为15 Hz的Ricker子波,炮间距为100 m,每一炮都是全地表等距(10 m)接收。接收记录长度为3 s,时间采样间隔为0.001 s。
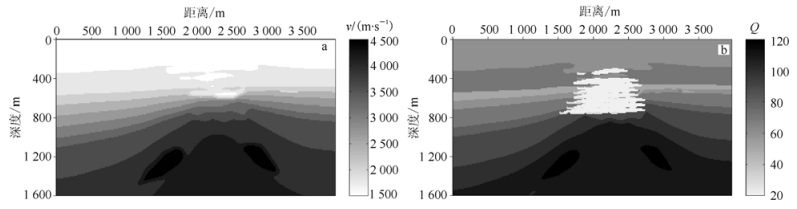 |
| 图 9 气云速度和Q模型 Fig.9 Gas chimney model with velocity and Q values |
采用高阶交错网格有限差分方法合成声波和黏声波地震记录。如图 10所示,选取一炮的正演结果,炮点位于1 000 m处。从图 10中可以看出,黏声波记录反射波的同相轴能量较弱,且同相轴的波形较宽;表明介质的黏滞性对地震波能量的吸收和衰减作用明显。图 11是对40炮记录所做的偏移结果。从图 11中可以看出,补偿后的能量强于没补偿的偏移剖面,接近参考偏移剖面,尤其在深部,并且补偿后的同相轴更连续。图 12是分别从图 11a,b,c的剖面上抽出的第100道(横向距离1 000 m处)和第200道(横向距离2 000 m处)的单道记录对比结果,由图可知,补偿后的振幅增强,相位得到校正。图 13为图 12对应的振幅谱,从频谱对比可以看到,黏滞声波高斯束叠前深度偏移有效地补偿了地震波的能量,尤其是中高频能量成分得到了加强,即相对声波叠前深度偏移结果,黏滞声波叠前深度偏移的分辨率要更高些。
 |
| a. 声波;b. 黏声波。 图 10 单炮记录(炮点位于水平距离1 000 m处) Fig.10 Synthetic data of one shot (at a distance of 1 000 m) |
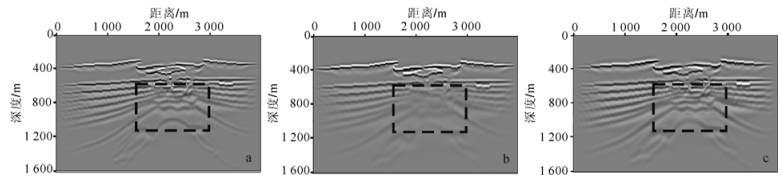 |
| a. 参考(声波正演,声波偏移);b. 未补偿(黏声波正演,声波偏移);c. 补偿后(黏声波正演,黏声波偏移)。 图 11 气云模型偏移叠加剖面 Fig.11 Migration results of Gas chimney model |
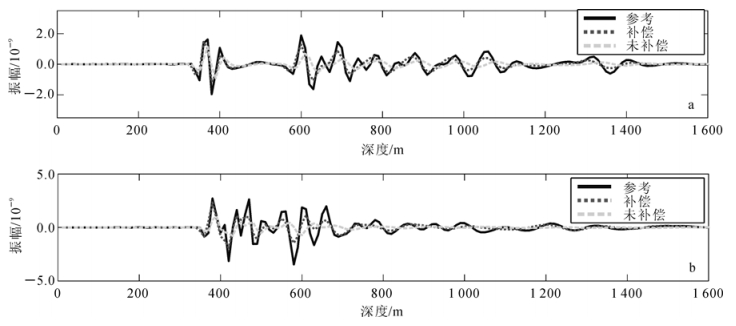 |
| a. 第100道;b. 第200道。 图 12 偏移剖面的单道波形对比 Fig.12 Comparison of the single trace waveforms extracted from image results |
高斯束偏移是一种优秀的偏移算法,基于高斯束偏移方法进行吸收衰减补偿,不仅具有Kirchhoff 偏移方法灵活高效的优点,而且具有接近于波动方程偏移的成像精度。笔者提出的黏滞声波高斯束叠前深度偏移可以补偿衰减对成像结果的影响。实算表明,新方法能有效提高分辨率,获得更好的成像剖面,尤其对于强吸收区域。
| [1] | Zhou J,Birdus S,Hung B,et al.Compensating Attenuation Due to Shallow Gas Through Q Tomography and Q-PSDM: A Case Study in Brazil[C]//81st Annual International Meeting. San Antonio: SEG, 2011: 3332-3336. |
| [2] | Bickel S H, Natarajan R R. Plane-Wave Q Deconvolution[J]. Geophysics, 1985, 50(9): 1426-1439. |
| [3] | Hargreaves N D, Calvert A J. Inverse Q Filtering by Fourier Transform[J]. Geophysics, 1991, 56(4): 519-527. |
| [4] | Wang Y H.Inverse Q Filter for Seismic Resolution Enhancement[J]. Geophysics, 2006, 71(3): 51-60. |
| [5] | 冯晅, 张瑾, 刘财, 等. 基于改进的 Kolsky 模型波场延拓公式的纵波Q值, 横波Q值估计[J]. 吉林大学学报:地球科学版, 2014, 44(1): 359-368. Feng Xuan, Zhang Jin, Liu Cai, et al. Estimation of P-and S-Waves Quality Factors Based on the Formula of the Wave-Field Continuation in Modified Kolsky Model[J]. Journal of Jilin University: Earth Science Edition, 2014, 44(1): 359-368. |
| [6] | Zhang C H, Ulrych T J. Refocusing Migrated Seismic Images in Absorptive Media[J]. Geophysics, 2010, 75(3): 103-110. |
| [7] | Mittet R, Sollie R, Hokstad K. Prestack Depth Migration with Compensation for Absorption and Dispersion[J]. Geophysics, 1995, 60 (5): 1485-1494. |
| [8] | Zhang J, Wapenaar K. Wavefield Extrapolation and Prestack Depth Migration in Anelastic Inhomogeneous Media[J]. Geophysical Prospecting, 2002, 50(10): 629-643. |
| [9] | Mittet R. A Simple Design Procedure for Depth Extrapolation Operators that Compensate for Absorption and Dispersion[J]. Geophysics, 2007, 72(2): 105-112. |
| [10] | Zhang J, Wu J, Li X. Compensation for Absorption and Dispersion in Prestack Migration: An Effective Q Approach[J]. Geophysics, 2013, 78(1): 1-14. |
| [11] | Hill N R. Gaussian Beam Migration[J]. Geophysics, 1990, 55: 1416-1428. |
| [12] | Hill N R. Prestack Gaussian-Beam Depth Migration[J]. Geophysics, 2001, 66: 1240-1250. |
| [13] | Hale D. Migration by the Kirchhoff, Slant Stack and Gaussian Beam Methods[R]. Golden: Colorado School of Mines Center for Wave Phenomena, 1992. |
| [14] | Hale D. Computational Aspects of Gaussian Beam Migration[R]. Golden: Colorado School of Mines Center for Wave Phenomena, 1992. |
| [15] | Gray S H. Gaussian Beam Migration of Common-Shot Records[J]. Geophysics, 2005, 70(4): 71-77. |
| [16] | Gray S H, Bleistein N. True-Amplitude Gaussian-Beam Migration[J]. Geophysics, 2009, 74(2): 11-23. |
| [17] | Popov M M, Semtchenok N M, Popov P M, et al. Depth Migration by the Gaussian Beam Summation Method[J]. Geophysics, 2010, 75(2): 81-93. |
| [18] | Cerveny V. A Note on Dynamic Ray Tracing in Ray-Centered Coordinates in Anisotropic Inhomogeneous Media[J]. Studia Geophysica et Geodaetica, 2007, 51: 411-22. |
| [19] | 岳玉波. 复杂介质高斯束偏移成像方法研究[D]. 青岛: 中国石油大学, 2011. Yue Yubo. Study on Gaussian Beam Migration Methods in Complex Medium[D]. Qingdao: China University of Petroleum, 2011. |
| [20] | Xie Y, Notfors C, Sun J, et al. 3D Prestack Beam Migration with Compensation for Frequency Depen-dent Absorption and Dispersion[C]//72nd EAGE Conference & Exhibition Incorporating SPE EUROPEC. Barcelona: [s. n.], 2010. |
| [21] | Keers H, Vasco D W, Johnson L R. Viscoacoustic Crosswell Imaging Using Asymptotic Waveforms[J]. Geophysics, 2001, 66: 861-870. |
| [22] | Zhu T Y, Harris J M, Biondi B. Q-Compensated Reverse-Time Migration[J]. Geophysics, 2014, 79(3): 77-87. |