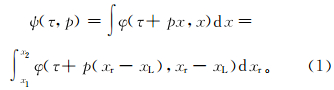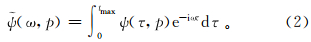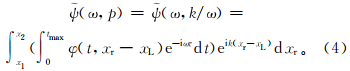2. 国土资源部应用地球物理综合解释理论实验室, 长春 130026
2. Laboratory for Integrated Geophysical Interpretation Theory, Ministry of Land and Resources, Changchun 130026, China
0 引言
平面波分解是在共炮道集或者共炮检距道集上,以最左端或者最右端为参考点所设置的绝对炮检距上进行的。沿着以一定射线参数和纵坐标轴截距时间所构成的叠加直线,将不同炮间距的振幅叠加,这样就实现了波场的平面波分解[1, 2, 3, 4, 5]。局部平面波分解是将共炮点道集或者是共炮检距道集上的一个接收点设为参考点(窗口中心道),并选取在参考点附近一定范围(窗口)内的其他接收道来进行平面波分解。在这个过程中以不同射线参数对原始的地震记录进行分选,一个射线参数对应一道的地震信息及每一道对应着一个入射角的平面波。新得到的道集,横坐标为射线参数,纵坐标为叠加直线在原坐标系纵轴上的截距时间[6, 7, 8, 9, 10]。因此,可以通过局部平面波分解将接收点处所接收到的波场分解为不同方向上的平面波波场,并且进行地震波场的反向延拓。局部平面波分解在偏移中也往往具有重要的意义:可以通过局部平面波分解来进行平面波偏移,同时它也是高斯波数偏移中的一个重要步骤,通过局部平面波分解可使高斯波数偏移具有方向选择性,从而提高偏移的成像精度[11, 12, 13, 14]。
局部平面波分解在提高成像效果的同时,也给计算机实现带来了很多困难。其中最大的困难是如何在高效地进行平面波分解的同时,精确地给出慢度方向和求取该慢度方向上每个时刻所对应的地震记录值,以减少后续偏移工作中的偏移噪声。局部平面波分解一般使用的是τ-p变换方法,在实现过程中包括3种实现方式:时间域下的实现方式、频率域下的实现方式和频率波数域下的实现方式。时间域下的局部平面波是直接将采集到的地震数据进行τ-p变换,从而获得不同慢度对应的地震记录。频率域下的局部平面波分解是先用傅里叶变换将地震记录变换到频率域下,然后将变换完的不同接收道的地震数据叠加为不同慢度所对应的频率数据,最后将这些频率数据再傅里叶反变换回时间域。频率波数域局部平面波分解是首先对地震记录做两次傅里叶变换,转换到频率波数域中,利用从频率域变换到波数域时的傅里叶变换来代替不同地震道的叠加,然后进行插值和重采样,求取不同慢度所对应的频率数据,最后将数据进行傅里叶反变换回时间域,得到倾斜叠加后的数据。相较于频率域和频率波数域下的局部平面波分解,时间域局部平面波分解不需要进行傅里叶变换和傅里叶反变换,但是却需要计算相似函数以减小计算误差。虽然频率波数域局部平面波分解可以用第二次的傅里叶正变换来替代不同地震道的叠加以达到减少计算量的目的,但是在进行插值重采样的时候,也增加了程序实现时的复杂性。
笔者根据这3种局部平面波分解算法的计算结果,对这些方法在实现过程中的计算精度和计算速度进行了讨论。简单介绍了局部平面波分解的理论基础;对于不同的地震记录,给出了不同局部平面波分解所得到的计算结果和用时;并对计算结果进行计算效率的分析、讨论和对比,以便在以后的实际应用中能够选择一种有效的局部平面波分解方法。
1 不同局部平面波分解方法的理论与实现对比根据波动理论,球面波可以被分解为无穷多的平面波;反之,平面波可以合成出球面波。如果球面波波前面远离点源,它总可以局部地视为一个平面波前。因此,尽管理论上平面波在现实世界中不存在,但我们可以用平面波的概念解释很多物理现象。近似地解决很多物理问题[1]。
1.1 时间域局部平面波分解原理在x-t域中,共炮点记录用φ(t,x)表示,x为每个接收道与中心道的距离,t为时间。一个共炮点记录包括N道记录,每道记录有M个采样点,可以看成一个二维数组,有N×M个数据。时间t对x的导数即为慢度p。通过p可以确定一条斜线,该斜线与t轴相交于一点,则有一个截距时间τ[1]。时间域局部平面波分解即为时间域τ-p变换,可表示为
式中:t=τ+px;x1、x2分别表示窗口左端和右端接收道的横坐标;xL为窗中心道的位置;xr为接收道的位置。式(1)的意义即沿t=τ+px的直线求和,将所得到的值放入τ-p坐标系内相应的点上。x-t域中的一条线,在τ-p坐标系内就成了一个点[1]。 1.2 频率域局部平面波分解原理频率域局部平面波分解是将地震记录通过傅里叶变换变到频率域内,对数据进行倾斜叠加,然后对数据进行傅里叶反变换,将其变回到时间域下。对式(1)中等号左端的τ做傅里叶变换:
其中:[0,tmax]为整个时间序列的定义域;ω为频率。将τ=t-px带入到式(2)中有

再用式(1)代替ψ(τ,p)即可得到
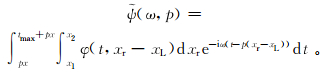
改变积分次序可得到
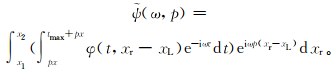
在实际应用中,时间序列是有限长的,因此会假设时间序列本身呈周期性,周期长度为序列长度。当原点的位置确定不变时,对序列[px,tmax+px]做傅里叶变换即等价于对[0,tmax]做傅里叶变换,故可以得到
式(3)中括号内的积分表示先对地震记录做傅里叶变换,使地震记录变到频率域下;括号外的积分表示对频率域的数据在不同地震道上做叠加。最后对φ(ω,p)做傅里叶反变换就能得到倾斜叠加的结果[5]。
1.3 频率波数域局部平面波分解原理由于频率波数域局部平面波分解是利用从频率域变换到波数域时的傅里叶变换来代替不同地震道的叠加,将波数k=ωp带入到(3)式中的e指数位置,可得到如下形式:
式(4)中括号内的积分表示先对地震记录做傅里叶变换,使地震数据变到频率域下;括号外的积分表示对频率域的地震记录做空间域的傅里叶反变换。由于频率波数域下的数据并不是p的函数,只存在p=k/ω的关系式,因此在求取p所对应的频率数据时,需要进行插值重采样。最后对插值重采样后的数据φ(ω,p)进行时间域傅里叶反变换就得到了频率波数域局部平面波分解的最后结果[8]。
1.4 不同方法的程序实现对比在时间域局部平面波分解的程序实现中,不需要对原始的时间域数据进行傅里叶变换,只需要在接中心接收道处先确定出一个慢度和一个截距时间,构造一个斜截式方程t=τ+px,求出该方程在不同接收道位置处所对应的时间;然后将(x, t)对应的能量加到τ-p域中(p,τ)所对应的位置即可。
在频率域局部平面波分解的程序实现中,首先要对原始的时间域数据进行傅里叶变换,将x-t的数据变换为x-ω的数据。然后在中心接收道处确定一个慢度,根据每一个接收道与中心道之间的距离确定每一个接收道的相移项(相位校正项)e-iωpx。此时,每一个固定的接收道中,不同的频率相移项是相同的。再将所有做完相移的接收道叠加到p-ω域中当前慢度所对应道。最后,对做完所有慢度叠加后的p-ω域数据进行傅里叶反变换,就可得到频率域局部平面波分解的结果。
在频率波数域局部平面波分解中,首先要对原始的时间域数据进行傅里叶变换,将x-t域的数据变换为x-ω域的数据。然后将x-ω域的数据以中心接收道为原点,对x进行一次傅里叶反变换,得到k-ω域的数据。此时,数据中ω是从正到负,而k都为正值。根据k=ωp,每一个确定的频率和确定的慢度都可以确定一个波数。然而波数是非连续性的,同时波数所对应的k-ω域内的数据也是震荡性的(在较小的定义域内存在有多个极值点),从而增加了插值的难度。一般需要进行sinc函数插值,将插值后得到数值映射到p-ω域内(p, ω)所对应的位置。最后将p-ω域的数据做傅里叶反变换,就可得到频率波数域局部平面波分解的结果。
对比3种方法可以发现,时间域局部平面波分解不需要进行傅里叶变换,而频率域和频率波数域局部平面波分解则需要进行傅里叶变换,将时间域下的地震记录变为频率域或者是频率波数域的地震记录进行计算。因此,时间域局部平面波分解是在时间域下进行不同道的叠加;频率域的局部平面波分解则在频率域下对不同道的记录进行叠加;频率波数域局部平面波分解也要比频率域局部平面波分解多一次傅里叶变换,通过多的这一次傅里叶变换来替代对不同道的叠加,然后进行插值重采样得到最后的计算结果。
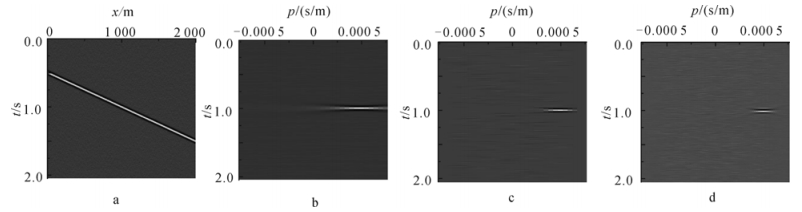
2 模型试算对比为了研究上述3种算法的计算精度和效果,给出一个慢度为0.000 5 s/m的同相轴的地震记录(图 1a)。地震记录共201道,道间距为10 m,采样时长为2.048 s,时间采样间隔为0.002 s。中心道取在1 000 m处,窗口长600 m。图 1b为时间域局部平面波分解的计算结果。可以看出,由于时间域是在地震记录上直接提取各慢度方向对应的地震记录,所以在接收时刻,每个慢度方向上都有能量显示,在正确的慢度方向上能量最大。图 1c为频率域局部平面波分解的计算结果,图 1d为频率波数域局部平面波分解的计算结果。由图 1可以看出:3种计算方法都能够很好地提取出波前到达接收点处的时间;但频率域和频率波数域的计算结果相对于时间域的计算结果具有明显的优势,能量更向正确的慢度方向上集中,而在正确的慢度方向两侧能量衰减更快。频率域和频率波数域局部平面波分解中,频率波数域局部平面波分解的效果更好。
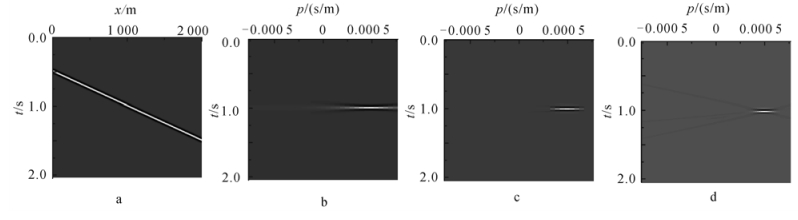 |
| a. 同相轴地震记录;b. 时间域倾斜叠加结果;c. 频率域倾斜叠加结果;d. 频率波数域倾斜叠加结果。图 1 p为0.000 5 s/m同相轴地震记录的局部平面波分解结果对比 Fig.1 1 Local plane wave decomposition comparison with the seismic data when p is 0.000 5 s/m |
图 2a为Marmousi理论模型第100炮的模拟数据。共96道,道间距为25 m,采样时长为2.900 s,时间采样间隔为0.004 s。局部平面波分解的窗口宽度为600 m,窗口中心取在300 m处。通过图 2b、c和d可以看出,3种方法都能够很好地计算出波前到达接收点处的时间以及入射的方向,相对来说时间域局部平面波分解的效果不如其他两种方法,能量团收敛相对不集中。由于没有在时间域的局部平面波分解的计算过程中加衰减窗,而是直接使用式(1)中的计算公式,所以时间域局部平面波分解的结果较频率域和频率波数域局部平面波分解的结果能量强。频率域和频率波数域局部平面波分解的计算效果差别不大,相对来说频率波数域局部平面波分解的计算结果中的能量团比频率域局部平面波分解中的结果更集中。
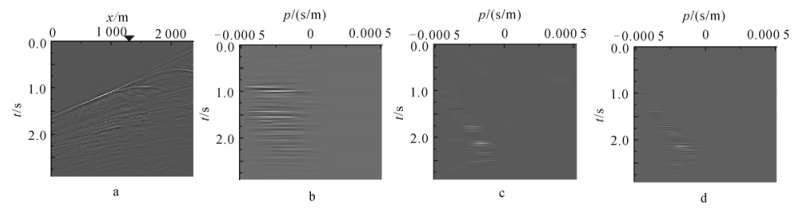 |
| a. 地震记录;b. 时间域倾斜叠加结果;c. 频率域倾斜叠加结果;d. 频率波数域倾斜叠加结果。 图 2 Marmousi模型第100炮地震记录在1 300 m处的局部平面波分解结果对比 Fig.2 Local plane wave decomposition comparison at 1 300 m with the 100th SP Marmousi data |
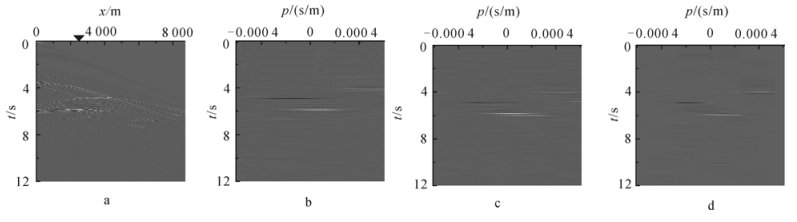
图 3是BP理论模型的第700炮的模拟数据。共1 201道,道间距为12.5 m,采样时长为12 s,时间采样间隔为0.006 s,其中局部平面波分解的窗口中心位于12 500 m处,窗口宽300 m。在图 3b、c和d中对应图 3a中近似双曲线的同相轴的位置上可以看到较为明显的同相轴,频率波数域局部平面波分解在能量聚焦效果上要优于其他两种方法。
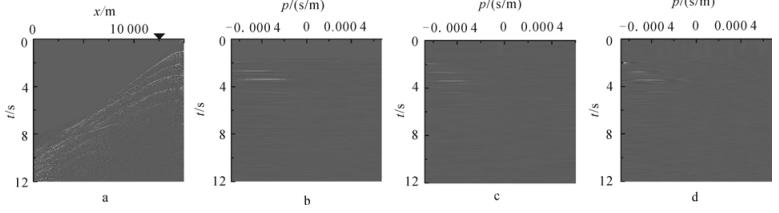 |
| 图 3 BP模型第700炮地震记录在12 500 m处的局部平面波分解结果对比 Fig.3 Local plane wave decomposition comparison at 12 500 m with the 700th SP BP data |
图 4是Sigsbee理论模型的第300炮的模拟数据。共348道,道间距为12.5 m,采样时长为12 s,时间采样间隔为0.008 s,其中局部平面波分解的窗口中心位于2 500 m处,窗口宽300 m。在图 4a中,中心道上既有斜率为正的同相轴,也有斜率为负的同相轴。在图 4b、c和d中,可以看出3种方法都能够很好地区分出不同能量团所对应的慢度和时间,而在能量团的收敛效果上同图 2和图 3类似,频率波数域的效果要优于另两种方法。为了检验3种方法的抗噪性,以图 1a中的数据为基础增加了高斯噪声。高斯噪声的频率为5~60 Hz。图 5a为慢度为0.000 5 s/m的同相轴地震记录。图 5b、c和d分别为时间域局部平面波分解、频率域局部平面波分解和频率波数域局部平面波分解的计算结果。由图 5可见:在计算效果上,图 5同图 1所得到的计算结果一致;而在抗噪性方面,3种方法都有着较好的抗噪能力,在能量聚焦的强弱方面和能量所对应时间和慢度的准确性上都没有受到噪声的干扰,依然能够很好地区分出能量团所对应的时间和慢度。
 |
| a. 地震记录;b. 时间域倾斜叠加结果;c. 频率域倾斜叠加结果;d. 频率波数域倾斜叠加结果。 图 4 Sigsbee模型第300炮地震记录在2 500 m处的局部平面波分解结果对比 Fig.4 Local plane wave Decomposition comparison at 2 500 m with the 300th SP Sigsbee data |
 |
| a. 同相轴地震记录;b. 时间域倾斜叠加结果;c. 频率域倾斜叠加结果;d. 频率波数域倾斜叠加结果。 图 5 增加了高斯噪声的p为0.000 5 s/m的同相轴地震记录局部平面波分解结果对比 Fig.5 Local plane wave decomposition comparison of the seismic data with p is 0.000 5 s/m and Gaussian noise |
为了对比3种算法的计算效率,分别计算了慢度为0.000 5 s/m的同相轴地震记录、Marmousi模型第100炮的地震记录、BP模型第700炮的地震记录和Sigsbee模型第300炮的地震记录。表 1显示了3种算法在计算不同地震记录时的CPU耗时。通过分析可以发现:频率波数域局部平面波分解的计算效率最高,其次是频率域局部平面波分解;计算效率最差的是时间域局部平面波分解。这是因为频率波数域局部平面波分解更多地使用了快速傅里叶变换来代替求和,从而减少了计算时间。频率域局部平面波分解虽然也使用了快速傅里叶变换,但是在计算过程中依然存在大量的求和过程,故而比频率波数域局部平面波分解的计算量大。
| s | |||
| 计算的数据 | 时间域 倾斜叠加 | 频率域倾斜叠加 | 频率波数域倾斜叠加 |
| p为0.000 5的 同相轴地震记录 | 0.296 | 0.246 | 0.082 |
| Marmousi模型第100炮 地震记录1 300 m处 | 0.288 | 0.235 | 0.079 |
| BP模型第700炮 地震记录12 500 m处 | 0.875 | 0.828 | 0.282 |
| Sigsbee模型第300 炮 地震记录2 500 m处 | 0.375 | 0.250 | 0.080 |
笔者介绍了时间域、频率域和频率波数域下3种局部平面波分解算法的特点,分析对比其在倾斜叠加方法中的实现方法,并对这些方法的计算结果进行对比分析。可以得到如下结论:
1)在时间域、频率域和频率波数域3种局部平面波分解算法中,频率波数域局部平面波分解算法的精度是最高的。
2)不同域下的局部平面波分解算法,由于采用的实现方法不同,计算效率也不相同。采用时间域和频率域局部平面波分解算法,在同一数据的计算用时相差不大,而频率波数域局部平面波分解算法则具有明显的计算速度优势。
综上所述,在倾斜叠加的过程中,局部平面波分解算法的选择直接影响着计算的精度和效率,选择一种既能满足计算精度又能满足计算效率的算法是十分关键的。从总体上讲:频率波数域局部平面波分解在计算精度和效率上优于时间域局部平面波分解,但是频率波数域局部平面波分解需要进行插值重采样,这个过程增加了计算的复杂性;频率域局部平面波分解的计算精度和计算效率均居中。
| [1] | 吴律. τ-p变换及应用[M].北京: 石油工业出版社, 1993. Wu Lü. Theory and Application of τ-p Transform[M]. Beijing: Petroleum Industry Press, 1993. |
| [2] | 孙成禹. 球面波分解理论及其倾斜叠加方法的实现[J]. 石油地球物理勘探, 2000,35(6): 723-729. Sun Chengyu. Theory of Spherical Wave Decomposition and Realization of Dip Stack[J]. Oil Geophysical Prospecting, 2000,35(6): 723-729. |
| [3] | Treitel S,Gutowski P,Wagner D.Plane-Wave Decomposition of Seismograms[J]. Geophysics, 1982,47(10): 1375-1401. |
| [4] | Yilmaz O.Seismic Data Processing[M].Tulsa: Society of Exploration Geophysicists, 1987. |
| [5] | Mithal R, Vera E. Comparison of Plane-Wave Decomposition and Slant Stacking of Point-Source Seismic Data[J]. Geophysics, 1987,52(12): 1631-1638. |
| [6] | Claerbout J F. Earth Soundings Analysis: Processing Versus Inversion[M]. Cambridge: Blackwell Scientific Publications, 1992. |
| [7] | Fomel S. Applications of Plane-Wave Destruction Filters[J]. Geophysics, 2002, 67(6): 1946-1960. |
| [8] | Fomel S. Shaping Regularization in Geophysical-Estimation Problems[J]. Geophysics, 2007, 72(2): 29-36. |
| [9] | 刘财,崔芳姿,刘洋,等. 基于低信噪比条件下新型Seislet变换的阈值去噪方法[J]. 吉林大学学报:地球科学版,2015,45(1):291-301. LiuCai,CuiFangzi,LiuYang,etal.ThresholdDenoi-singMethodBasedonNewSeisletTransformintheConditionofLow SNR[J].JournalofJilinUniversity:EarthScienceEdition,2015,45(1):293-301. |
| [10] | Schleicher J, Costa J, Santos L, et al. On the Estimation of Local Slopes[J]. Geophysics, 2009, 74(4): 25-33. |
| [11] | Hill N R. Gaussian Beam Migration[J]. Geophysics, 1990, 55(II): 1416-1428. |
| [12] | Tiernan H. Improving Plane-Wave Decomposition and Migration[J]. Geophysics, 1997, 62(1): 195-205. |
| [13] | Fomel S. Velocity-Independent Tme-Domain Seismic Imaging Using Local Event Slopes[J]. Geophysics, 2007, 72(3): 139-147. |
| [14] | Gray S H, Bleistein N. True-Amplitude Gaussian-Beam Migration[J]. Geophysics,2009, 74(2): 11-23. |