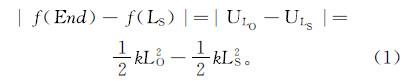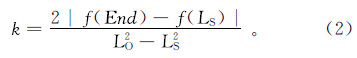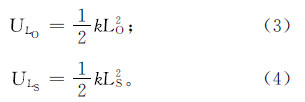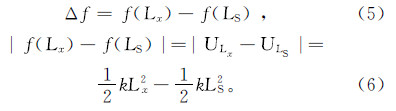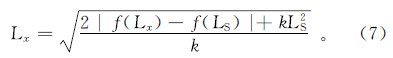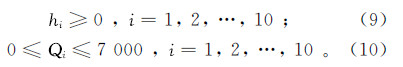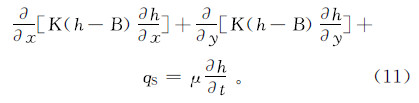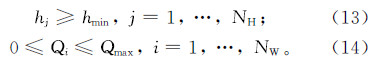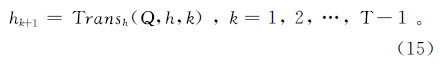2. 北京大学工学院水资源研究中心, 北京 100871
2. Center for Water Research, College of Engineering, Peking University, Beijing 100871, China
0 引言
地下水管理模型的求解是地下水资源科学管理的重要问题。地下水管理模型是寻求最少的社会经济环境成本来满足既定的管理目标[1, 2]。长期以来用于地下水管理模型求解的方法如单纯形法、最速下降法、高斯-牛顿法等都是针对连续的、可导的目标函数的,处理的问题比较简单,优化结果的质量强烈依赖初始解。由于遗传算法(genetic algorithm,GA)[3, 4, 5, 6]、禁忌搜索算法[7]、模拟退火算法[8]、粒子群优化算法[2, 9]、蚁群优化算法[10]、模拟谐振子算法(simulated harmonic oscillator algorithm,SHOA)[11, 12, 13]等人工智能算法不受优化问题满足连续性和可导性的限制,且具有一定的全局寻优能力,因而逐渐被应用到地下水优化管理模型求解的领域。然而地下水管理模型常常表现出多维、非线性等复杂特征,因此开发针对地下水优化管理问题的高效算法十分必要。
笔者针对遗传算法和模拟谐振子算法的不足,结合传统的模拟谐振子算法和遗传算法的优点,首次提出了一种新型的谐振子遗传算法(harmonic oscillator genetic algorithm,HOGA),将其与地下水管理模型相结合;并将HOGA分别应用于理想算例和华北平原典型区地下水资源管理模型的算例中进行对比,以期了解其在地下水管理模型方面的应用前景。
1 谐振子遗传算法 1.1 谐振子遗传算法的基本原理遗传算法属于进化算法的一种,它通过模仿自然界的选择与遗传的机理来寻找最优解,McKiney和Lin[3]首先将其应用到地下水管理模型的求解中,取得了很好的效果。遗传算法具有良好的全局搜索能力,可以快速地搜索解空间,从而不会陷入局部最优解的快速下降陷阱。但是遗传算法的局部搜索能力较差,导致单纯的遗传算法比较费时,在进化后期搜索效率较低。在实际应用中,遗传算法容易产生早熟收敛的问题。采用何种选择方法既要使优良个体得以保留,又要维持群体的多样性,一直是遗传算法中较难解决的问题。
模拟谐振子算法(SHOA)是由模拟自然谐振子的物理规律而得到的一种通用的随机搜索算法[11]。对于图1所示的谐振子,当弹簧质点运动到左右端点位置时,弹性势能达到最大,等于系统的总能量;当弹簧质点处于振源位置时,弹性势能最小(等于0)。将弹簧质点的势能状态与优化问题中的目标函数相对应,当弹簧质点到达振源位置时,势能处于最小值的基态,对应的目标函数值即为找到的最优解。SHOA既具有良好的局部搜索能力,又具有较好的全局搜索能力。它在整个解空间范围内广泛地随机搜索近似最优解,而且以一定的规则接受差解,使领域解在局部山峰间平行跳跃,从而有效地控制了算法在全局范围内搜索的随意性[11, 12, 13],但因此也给算法的寻优效率带来了问题。针对遗传算法和模拟谐振子算法的不足,笔者综合模拟谐振子算法和遗传算法的优点,提出了一种新的算法谐振子遗传算法(HOGA)。HOGA利用模拟谐振子算法中的能级接受准则,对遗传算法中种群的选择策略进行了改进,同时利用模拟谐振子的领域解在局部山峰间的平行跳跃能力,有效地控制了遗传算法的早熟问题。
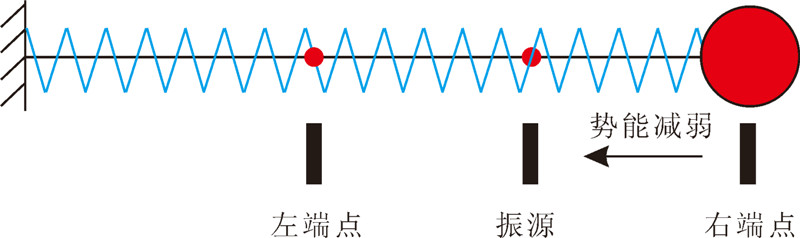 |
| 图 1 简谐振动谐振子示意图 Fig. 1 Oscillator of a simple harmonic oscillation |
| |
设谐振子遗传算法求解的是最大值问题,则求解地下水管理模型的步骤为:
1)随机产生种群规模为p的初始群体P(m),m为进化代数,同时确定谐振子的振幅A,初始步长LO、基态步长LS。
2)调用水流模型/运移模型计算适应度值。
3)根据群体适应度的最优值和最差值建立谐振子模型,确定谐振子端点End和振源Init。振子端点End处的势能ULO对应适应度的最差值f(End);基态步长处的势能为ULS,对应为适应度的最优值f(LS)。通过最优值和最差值之差的绝对值来确定谐振子的弹性系数k:
即求出k之后,就可以确定端点处势能和基态步长处的势能:
4)计算种群内所有染色体对应的能级Lx,对其中任意一条染色体,其适应度值为f(Lx),则
则其在谐振子中对应的位置,也就是能级为5)若Δf≥0,则该染色体不需要经过遗传算法的选择、交叉、变异,直接进入下一代;若Δf < 0,且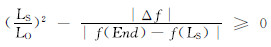 ,即Lx <
,即Lx < 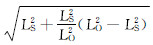 ,则该染色体也不需要经过遗传算法的选择、交叉、变异,直接进入下一代;否则,对第1条到第p(1-LS/LO)条染色体需要经过遗传算法的选择、交叉、变异之后再进入下一代,对第p(1-LS/LO)+1条到第p条染色体需要以概率(LS/LO)进行随机变异之后再进入下一代种群。
,则该染色体也不需要经过遗传算法的选择、交叉、变异,直接进入下一代;否则,对第1条到第p(1-LS/LO)条染色体需要经过遗传算法的选择、交叉、变异之后再进入下一代,对第p(1-LS/LO)+1条到第p条染色体需要以概率(LS/LO)进行随机变异之后再进入下一代种群。
6)终止条件判断,若不满足终止条件,则m=m+1,形成下一代种群,转移到第2)步,继续进行谐振子遗传算法相关的能级判断、选择、交叉、变异等操作过程;若满足终止条件,则输出当前最优个体,算法结束。
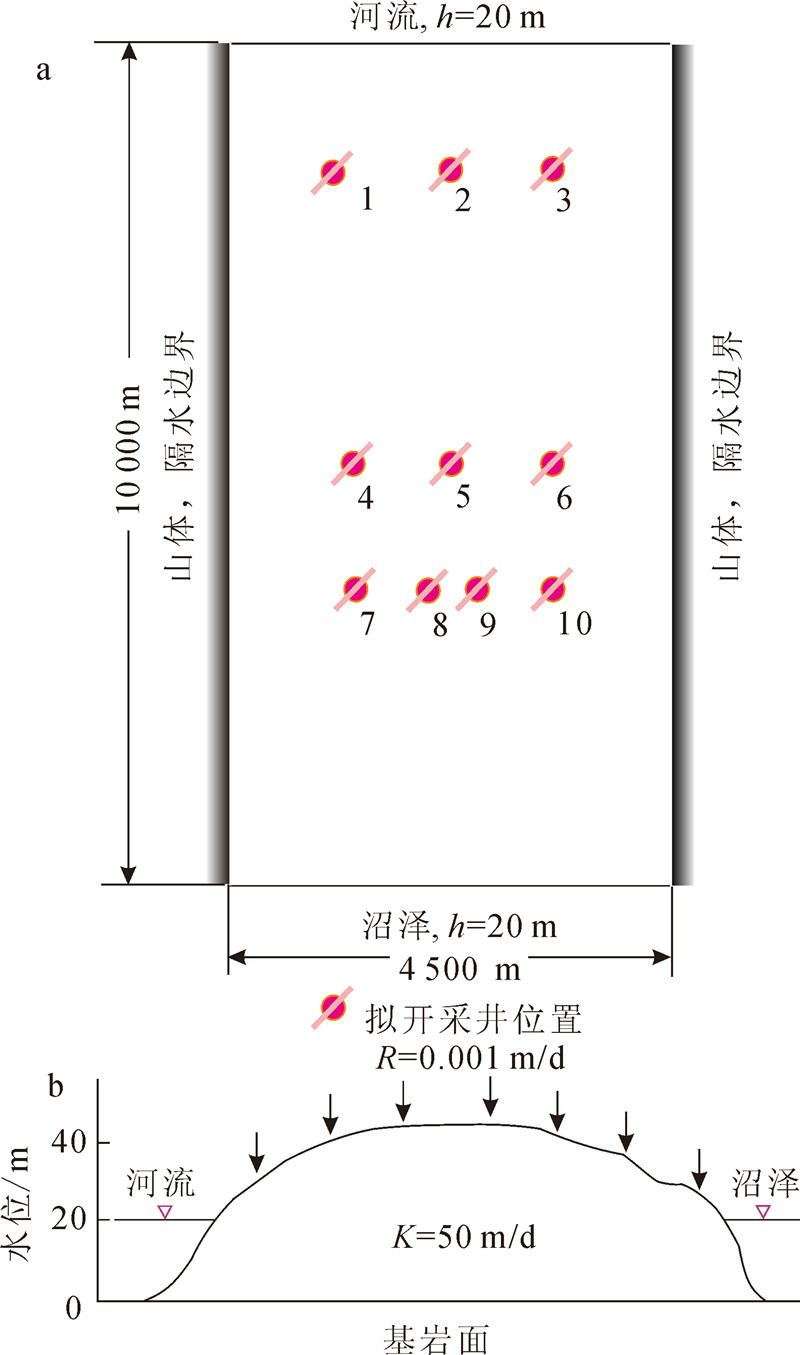
2 算例应用 2.1 理想算例在某潜水含水层上拟建一水源地,含水层中地下水为二维稳定流[3],如图2。含水层底板水平,其南部和北部边界分别为水沼地和河流,其水位均为20m,可作为第一类边界;东部和西部边界都为山体,作为隔水边界。设含水层介质均质各向同性,渗透系数K=50 m/d,单位面积上的补给量R=0.001 m/d,共有10眼拟开采井,假设每口井的允许开采量为7 000 m3/d,求满足该水源地含水层不致疏干情况下的最大可供水量(不考虑水井本身的释水能力)。 管理模型可表示为:
约束条件为: 其中:Qi为单井的抽水量(m3/d); hi为水位(m)。这个例子的目标函数是个线性的决策变量,当水头用hi2来进行约束时,约束条件也是线性的[3],McKiney和Lin用传统线性规划的方法求得最优解为59.3×103m3/d。本研究中,为增加算例的复杂性,含水层在空间上剖分成1 001行和451列,模拟时间设为899 000 d,总共1 000个应力期。GA和HOGA最大代数均设为120,种群数设为100,为了便于对比,SHOA目标函数每计算100个解后统计一次最优结果,搜索新解的上限为12 000个,采用GA、SHOA和HOGA分别求解的优化过程及结果如图3,最大抽水量、收敛代数和计算时间的结果如表1。管理模型的优化结果表明:相比于SHOA,GA的寻优速度更快,计算时间更短,在第70代找到了最优解,但容易陷入局部最优解的陷阱中; SHOA的寻优速度比GA慢,在第101代才找到最优解,但全局寻优性能优于GA,最后找到了比GA更好的解; HOGA在第46代即找到了最优解,寻优速度最快,是SHOA寻优速度的2.14倍,而且有极强的全局寻优能力,最优解优于GA和SHOA,比GA增加了供水量1.1×103m3/d,比SHOA增加供水量0.2×103m3/d。
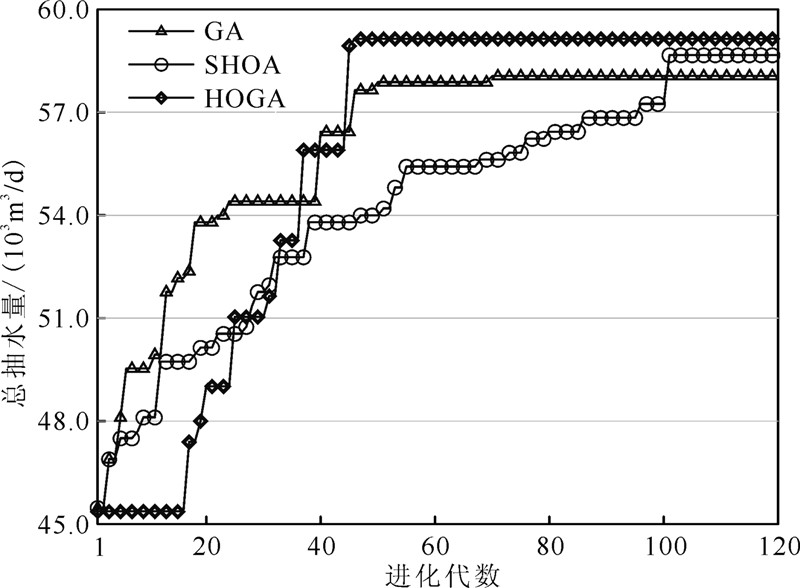 |
| 图 3 不同算法在最大化抽水量算例中的求解进化过程 Fig. 3 Evolution of the total pumping rates over the generations of the different algorithms |
| |
华北平原主要是指黄河以北、西倚太行山、东临渤海的广大平原地区;行政区划分属北京市、天津市和河北省,并涉及山东、河南两省的部分地域,面积约13.9 万km2,是我国北方重要的粮棉产地。该区大部分地区特别是大中城市处于地下水超采或严重超采状态,水资源匮乏和水环境恶化已经成为制约社会经济发展的主要因素。为此,Liu等[14]以石家庄市(包括城区和7个郊县)作为典型地区建立了该区地下水的水流模型,该水流模型不但刻画了研究区开采前的天然状态(补排均衡阶段),而且再现了研究区不同开采时期(包括漏斗形成和发展阶段[14])的水位变化过程,具有比较高的可信度,并从水量的角度建立了该区基于遗传算法的地下水资源可持续利用的管理模型。笔者采用HOGA对Liu等[14]建立的研究区地下水管理模型进行求解,并与GA和SHOA的求解效率进行对比,进一步验证HOGA在地下水管理模型中的可行性。
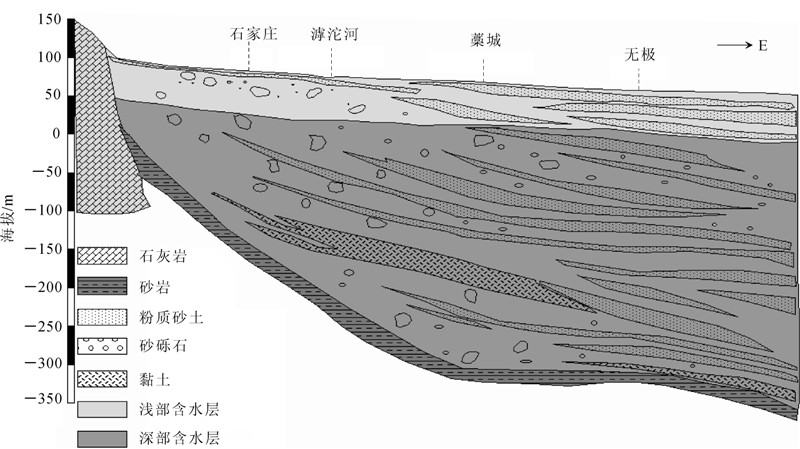
研究区包括石家庄市市区及正定、滦城、无极、藁城、赵县、元氏和晋州7县的部分区域(图4),位于太行山南麓,属于滹沱河冲洪积扇的中上部地带,地势西高东低,由西向东缓慢倾斜,面积约为4 000 km2。研究区处于滹沱河以黄壁庄为顶点的冲积扇的中上部,地下水主要赋存于第四系松散岩层孔隙中,自上而下可分为:全新统(Q4)、上更新统(Q3)、中更新统(Q2)和下更新统(Q1)共4个含水层组。上部的两个含水层组之间无连续的隔水层,水力联系密切,统称为浅部含水层;下部的两个含水层组岩性主要为含黏土卵砾石、砾石夹土层,分选性和富水性都很差,统称深部含水层,如图5所示。从总体上看:研究区含水层在水平方向上,由西向东含水层总厚度由薄变厚,粒度由粗变细,层次由少增多,单层厚度变薄,分选性由差变好,富水性由强变弱;在垂直方向上,含水层上下部粒度较细,厚度较小,中部粒度较粗,厚度也较大。随着开采规模的不断扩大,实际上以上各含水层之间都存在着密切的水力联系。
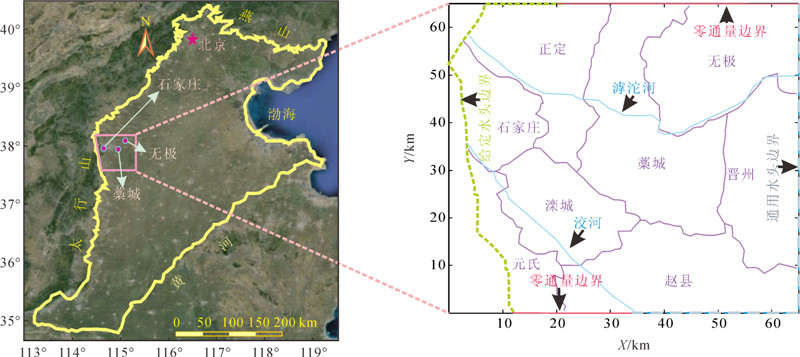 |
| X、Y分别表示东西方向和南北方向的距离。 图 4 研究区位置及水文地质概念模型 Fig. 4 Location of the study area and the hydrogeological conceptual model |
| |
地下水的补给主要有大气降水、地表水的入渗、侧向补给及农田灌溉回归水等。1965年前,石家庄市区内地下水处于天然状态下,由西或西北方向往东或东南方向流动,且自西向东,含水层介质颗粒由粗变细,含水单层由厚变薄,含水层数由少变多,水量和水力坡降由大变小,补给径流条件和水质由好变差,具典型的平原水文地质特点。之后随着地下水开采量的增大,地下水的排泄方式逐渐转变为以人工开采为主,其次为向下游的侧向径流排泄。随着市区地下水降落漏斗范围的扩大和地下水位埋藏深度的增加,人工开采几乎已成为目前唯一的地下水排泄方式[14, 15, 16, 17, 18, 19]。
2.2.2 研究区地下水模拟-优化管理模型诸多研究[13, 14, 15, 16, 17]表明研究区浅层地下水和深层地下水之间具有统一的水力联系,因此整个含水系统可以概化为单层的非均质各向同性的二维水流运动。在边界上,含水系统接受外界侧向补给或往外排泄;在裸露区接受大气降水入渗或农业灌溉回渗,同时在区域内最主要的排泄方式为人工开采。1960年以前,研究区地下水流处于天然状态,人工开采可忽略不计,地下水流可近似认为做稳定流动;1960年以后,随着地下水开采规模的加大,研究区地下水流不再处于天然状况,而是对应于不同边界条件和源汇项的非稳定运动。相应地,描述研究区地下水流运动的微分方程可表示为
其中:h为水头(m); t为时间(d); B为含水层的底板标高(m);qS为源汇项(d-1); μ为给水度(无量纲)。再加上相应的初始条件,这样,微分方程与边界条件和初始条件一起就构成了描述研究区地下水流运动的数学模型[13]。模拟时间从1959年到2004年,总共63个应力期;模型在空间上剖分成130行和135列,每个网格的边长均为500 m。用MODFLOW[20]对模型进行求解,详细的水流模型参见文献[14]。
基于以上地下水模拟模型的最大化开采量的管理模型可表述为
约束条件: 式中:Qmax表示抽水井i的最大出水能力(m3/d);hj表示约束点j处的水位(m);hmin表示在点j处的水位最低约束值(m);NT为管理期的数目;NH,NW分别表示水位约束点和抽水井的数目;Δtk表示每个管理期的时长(d)。当然,管理模型还要耦合上述地下水模拟模型(微分方程(11)及其定解条件),可简单地表示为
式中:hk表示研究区地下水在k时段的水位分布;Transh代表水头由k时段到k+1时段的状态转移函数;T为时段总数。式(15)表示系统在(k+1)时刻的状态变量h是其k时刻状态变量h及其决策变量Q两者的函数。 2.2.3地下水优化管理模型的求解求解管理模型时,GA和HOGA最大代数均设为100,种群数设为1 000,为便于比较,SHOA目标函数每计算1 000个解后统计一次最优结果,搜索新解的上限为10万个,采用GA、SHOA和HOGA分别求解的优化过程及结果如图6,最大抽水量、地下水超采量、收敛代数和计算时间的结果如表2。
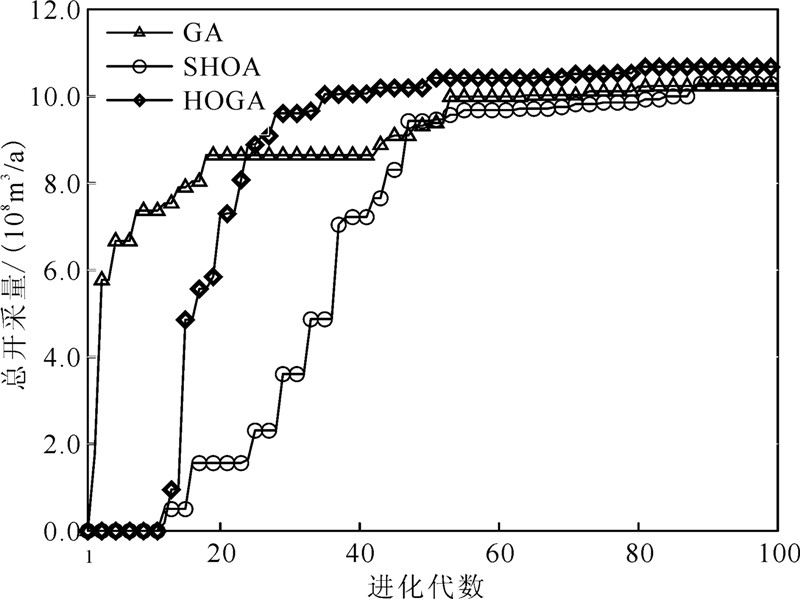 |
| 图 6 不同算法在华北平原地下水管理模型优化算例中的求解进化过程 Fig. 6 Evolution of the total pumping rates over the generations of the different algorithms in North China Plain |
| |
| 对比项目 | 优化方法 | |||
| GA | SHOA | HOGA | ||
| 最优解/(108 m3/a) | 10.22 | 10.29 | 10.69 | |
| 地下水超采量/(108 m3/a) | 4.75 | 4.67 | 4.27 | |
| 达到最优解的计算代数 | 80 | 89 | 80 | |
| 计算时间/h | 43.35 | 88.97 | 43.57 | |
GA和HOGA都在约80代达到最优解,而SHOA则在第89代达到最优解,表明HOGA的搜索速度和计算效率继承了遗传算法的优点,比原来的SHOA有了很大的提高。GA最优解为10.22×108 m3/a,和2004年实际开采量[13]的14.97×108 m3/a对比,地下水超采量达到4.75×108 m3/a;SHOA最优解为10.29×108 m3/a,地下水超采量达4.67×108 m3/a;HOGA的最优解为10.69×108 m3/a,地下水超采量为4.27×108 m3/a,相比GA增加供水量0.47×108 m3/a,相比SHOA增加供水量0.40×108 m3/a,地下水超采量得到较大降低。由此表明HOGA的全局搜索能力有了极大的提高,均强于GA和SHOA的搜索能力。
3 结论针对模拟谐振子算法和遗传算法的不足,提出一种新型的谐振子遗传算法。谐振子系统势能收敛到基态所特有的物理性质能保证谐振子遗传算法最后的收敛性,并通过谐振子对新解的接受准则来对使种群朝着最优的方向进化,使得谐振子遗传算法优化寻优结果的质量和计算效率均有很大提高。
谐振子遗传算法应用于地下水管理模型的求解结果表明:对于理想算例,谐振子遗传算法表现出了很强的全局寻优能力和搜索效率;在华北平原典型区地下水资源的优化算例中,谐振子遗传算法全局寻优能力在很大程度上超过了遗传算法和模拟谐振子算法,相对于模拟谐振子算法,搜索效率也有很大的提高。表明谐振子遗传算法不仅对理想算例的寻优具有很好的效果,而且对区域性复杂算例的地下水资源优化问题也有很强的优势。
谐振子遗传算法融合了遗传算法和模拟谐振子算法的优点,对初始解没有太大的依赖性,通用性较强,可推广应用于水文地质参数识别、地下水污染源识别、地下水污染修复等优化管理领域。
| [1] | 杨蕴,吴剑锋,吴吉春. 两种智能算法在求解地下水管理模型中的对比[J].吉林大学学报:地球科学版, 2009, 39(3):474-502.Yang Yun, Wu Jianfeng, Wu Jichun. A Comparative Study of Two Intelligent Optimization Techniques for Groundwater Management Modeling[J]. Journal of Jilin University:Earth Science Edition, 2009, 39(3): 474-502. |
| [2] | 骆乾坤,王佩,朱国荣. 水文地质参数识别的快速和谐搜索算法[J].水文地质工程地质, 2011, 38(4):14-19.Luo Qiankun,Wang Pei, Zhu Guorong. Fast Harmony Search Algorithm and Its Application to Hydrogeological Parameters Identification[J]. Hydrogeology & Engineering Geology, 2011, 38(4):14-19. |
| [3] | McKinney D C, Lin M D. Genetic Algorithm Solution of Groundwater Management Models[J]. Water Resources Research, 1994, 30(6): 1897-1906. |
| [4] | 吴鸣,吴剑锋,林锦,等.地下油罐泄漏区污染源的自动识别[J].环境科学学报, 2013, 33(12): 3251-3259.Wu Ming, Wu Jianfeng, Lin Jin, et al. Automated Identification of the Unknown Contaminant Source in Groundwater at a Leaking Underground Storage Tank Site[J]. Acta Scientiae Circumstantiae, 2013, 33(12): 3251-3259. |
| [5] | 吴剑锋,朱学愚,钱家忠,等. GASAPF方法在徐州市裂隙岩溶水资源管理模型中的应用[J]. 水利学报, 2000, 31(12):7-13.Wu Jianfeng, Zhu Xueyu, Qian Jiazhong, et al. Application of GASAPF to Optimization Model for Fracture Karst Water Resources Management[J]. Journal of Hydraulic Engineering, 2000,31(12): 7-13. |
| [6] | 林锦,郑春苗,吴剑锋,等. 基于遗传算法的变密度条件下地下水模拟优化模型[J]. 水利学报, 2007,38(10):1236-1244.Lin Jin, Zheng Chunmiao, Wu Jianfeng, et al. Ground Water Simulation Optimization Model Based on Genetic Algorithm Under Variable Density Conditions[J]. Journal of Hydraulic Engineering, 2007,38(10): 1236-1244. |
| [7] | 杨蕴,吴剑锋,于军,等. 基于参数不确定性的地下水污染治理多目标管理模型[J]. 环境科学学报, 2013, 33(7):2059-2067.Yang Yun, Wu Jianfeng, Yu Jun, et al. A Multi-Objective Simulation-Optimization Model for Optimal Design of Groundwater Remediation Systems Under Uncertainty[J]. Acta Scientiae Circumstantiae, 33(7): 2059-2067. |
| [8] | 高利平,何敬宇. 模拟退火算法在边坡稳定分析中的应用研究[J].内蒙古农业大学学报, 2010, 31(4):218-221.Gao Liping, He Jingyu. The Application and Investigation of Simulated Annealing Method in the Analysis of Slope Stability[J]. Journal of Inner Mongolia Agricultural University, 2010, 31(4): 218-221. |
| [9] | 刘贺,张弘强,刘斌. 基于粒子群优化神经网络算法的深基坑变形预测方法[J].吉林大学学报:地球科学版, 2014, 44(5):1609-1614.Liu He, Zhang Hongqiang, Liu Bin. A Prediction Method or the Deformation of Deep Foundation Pit Based on the Partical Swarm Optimization Neural Network[J]. Journal of Jilin University: Earth Science Edition, 2014,44(5): 1609-1614. |
| [10] | 秦永波,王鹏,肖黎彬,等. 量子谐振子蚁群算法[J]. 计算机应用, 2011, 31(2):54-69.Qin Yongbo, Wang Peng, Xiao Libin, et al. Ant Colony Optimization of Quantum Harmonic Oscillators[J]. Journal of Computer Applications, 2011, 31(2): 54-69. |
| [11] | 倪霖,段超,钟辉. 基于模拟谐振子算法的多项目调度[J]. 计算机应用, 2011,31(9):2559-2562.Ni Lin, Duan Chao, Zhong Hui. Multi-Project Scheduling Based on Simulated Harmonic Oscillator Algorithm[J]. Journal of Computer Applications, 2011, 31(9): 2559-2562. |
| [12] | 王培崇,钱旭. 模拟谐振子算法及其全局收敛性分析[J]. 计算机工程, 2013,39(3):209-212.Wang Peichong, Qian Xu. Simulated Harmonic Oscillator Algorithm and Its Global Convergence Analysis[J]. Computer Engineering, 2013,39(3): 209-212. |
| [13] | 程勖,李文辉,刘裕斌. 基于模拟谐振子算法的服务调度技术[J].大连海事大学学报. 2013, 39(2):78-81.Cheng Xu, Li Wenhui, Liu Yubin. Service Scheduling Technique Based on Simulated Harmonic Oscillator Algorithm[J]. Journal of Dalian Maritime University, 2013,39(2): 78-81. |
| [14] | Liu J, Zheng C M, Li Z, et al. Ground Water Sustainability: Methodology and Application to the North China Plain[J]. Ground Water, 2008, 46(6):897-909. |
| [15] | Cao G L, Zheng C M, Scanlon B R, et al. Use of Flow Modeling to Assess Sustainability of Groundwater Resources in the North China Plain[J]. Water Resources Research, 2013, 49: 1-17. |
| [16] | Wang B G, Jin M G, Nimmo J R, et al. Estimating Groundwater Recharge in Hebei Plain, China Under Varying Land Use Practices Using Tritium and Bromide Tracers[J]. Journal of Hydrology, 2008, 356:209-222. |
| [17] | 张光辉,费宇红,张行南,等. 滹沱河流域平原区地下水流场异常变化与原因[J].水利学报. 2008, 39(6):747-752.Zhang Guanghui, Fei Yuhong, Zhang Xingnan, et al. Abnormal Variation of Groundwater Flow Field in Plain Area of Hutuo River Basin and Analysis on Its Cause[J]. Journal of Hydraulic Engineering, 2008, 39(6):747-752. |
| [18] | 冯慧敏,张光辉,王电龙,等.近50年来石家庄地区地下水流场演变驱动力分析[J].水利学报. 2014, 45(2):180-186.Feng Huimin, Zhang Guanghui, Wang Dianlong, et al. Analysis on Driving Force for Groundwater Flow Field Evolution in Shijiazhuang Area in Recent 50 Years[J]. Journal of Hydraulic Engineering, 2014, 45(2):180-186. |
| [19] | 费宇红,张光辉,刘克岩,等.华北平原河道地下调蓄与利用潜力[J].吉林大学学报:地球科学版, 2011, 41(增刊1):265-271.Fei Yuhong, Zhang Guanghui, Liu Keyan, et al. The Adjustment of Groundwater Storage and Utilization Potential of River Channel in North China Plain[J]. Journal of Jilin University: Earth Science Edition, 2011, 41(Sup.1):265-271. |
| [20] | Harbaugh A W. MODFLOW-2005, The US Geological Survey Modular Ground-Water Model:The Ground-Water Flow Process[R]. Reston: U S Geological Survey, 2005. |