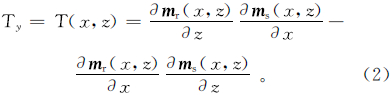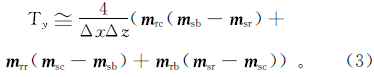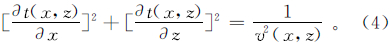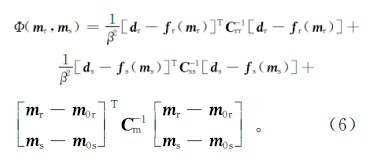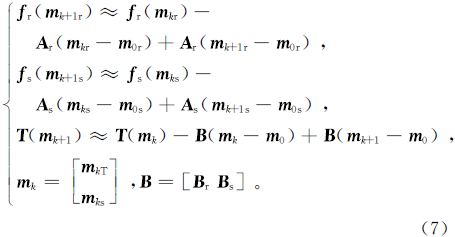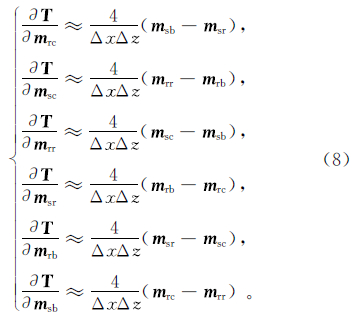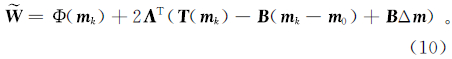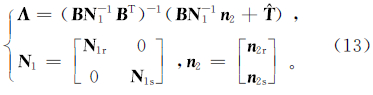2. 金策工业综合大学资源探测工学系, 朝鲜 平壤 999093
2. Resource Exploration and Engineering Department, Kimchaek University of Technology, Pyongyang 999093, Korea
0 引言
单一的地球物理方法仅反应相应的物性分布,且每种地球物理方法的物理模型修复特征不同。联合反演是结合多种地球物理场数据,通过反演地下的物性参数和几何形态得到相同地质体[1, 2]。联合反演的参数耦合基本分为2类:1)基于物性的耦合。像直流电阻率法与大地电磁法同一物性的联合反演,或利用经验及分析岩石物理关系的联合反演,如文献[3, 4]实现了大地电磁测深法和重力以及地震数据间的二维联合反演。2)空间分布结构性耦合,与物性梯度方向无关的结构约束联合解释是以曲率差为约束条件进行反演[5, 6]。如文献[7]实现了直流电阻率和地震数据的联合反演,将交叉梯度加入到目标函数中用来约束不同参数之间的关系,该方法不依赖先验信息即可耦合本质上不同的地球物理资料并进行解释;文献[8]完成了对magnetotelluric(MT)和地震间的三维交叉梯度联合反演。
笔者先从交叉梯度数学的算法出发,对其基本理论进行剖析;再编写大地电磁测深和地震初至波走时联合反演程序,模拟研究大地电磁测深和地震初至波走时二维联合反演,并将联合反演结果和单独反演结果进行对比。
1 基本理论和算法 1.1 交叉梯度将交叉梯度函数应用于电阻率和速度间的联合反演中,定义函数为
其中:▽为梯度;mr为电阻率的对数;ms为速度或慢度; ▽mr(x,y,z)和▽ms(x,y,z)分别为电阻率对数和慢度在点(x,y,z)处的梯度。物性参数的梯度表示在该点变化最快的方向,其大小为变化率。若模型参数mr和ms在(x,y,z)处的夹角为0°或180°,则函数值[9]为

若▽mr(x,y,z)和▽ms(x,y,z)中有1个为0,则T=0。
1.2 交叉梯度的离散化交叉梯度函数是二阶非线性方程,不存在不连续点和奇异点。令地质体走向沿y方向。此时模型参数对y求偏导数均为0,因此T仅在y分量上有函数值,Tx=Tz=0,则式(1)可表示为
式中,Tx、Ty、Tz分别为T在x,y,z三个方向上的分量。
地下2D网格化模型结构如图 1所示:Δx和Δz分别为单元的宽度和高度;mrc,mrr,mrb,msc,msr,msb分别为中心块、右边块、下边块的电阻率的对数和慢度。采用前向差分法[10]对公式(2)进行离散化处理,可得
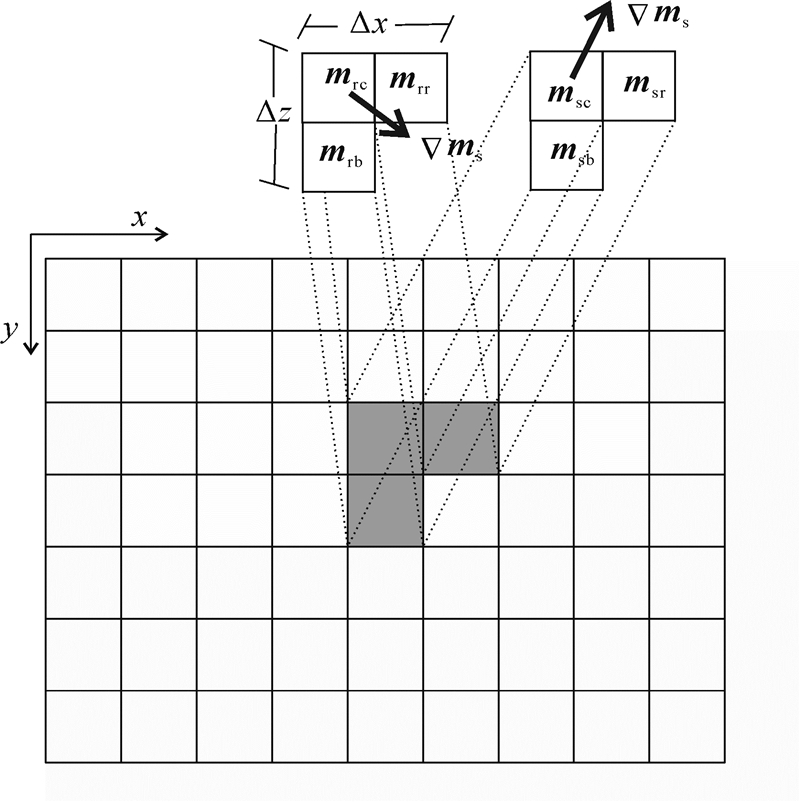 |
| 图 1 地下2D网格化模型结构 Fig. 1 Underground 2D grid model structure |
| |
地震波走时可通过对Eikonal方程
数值求解得到。式中:t为时间;v为速度。本文采用有限差分法[11, 12]求解方程(4)。
雅克比矩阵是由走时对模型慢度求导所得,对于一个给定的射线,走时的表达式为
其中:lj为第j个单元内的射线长度;msj为第j个单元内的慢度。由式(5)可见,雅克比矩阵可通过计算射线路径求得。本文地震走时采用FAST(first arrival seismic tomography)程序,该程序可计算二、三维的初至波走时和雅克比矩阵。
1.3.2 大地电磁法二维正演和雅克比矩阵由电磁理论可知,在非均匀地电结构中,大地电磁场由一次场和二次场组成。其中一次场为背景产生的场,二次场为异常体产生的场。由二次场的麦克斯韦方程可得两种模式transverse electric polarization(TE)和transverse magnetic polarization(TM)的表达式,通过推导麦克斯韦方程可得两种模式下二次场的赫姆霍兹方程。再用有限元法求解偏微分方程[13]即可实现大地电磁二维正演。文献[14]给出了大地电磁二维有限元正演的算法并编程实现,由于正演的计算需要有限单元网格,因此对地下模型进行了网格化,且每个网格内的电导率是均匀的。
利用互换原理[15]计算地下电导率的大地电磁测深响应的雅克比矩阵,对赫姆霍兹方程中每个反演单元的电导率求导,结果与分布在网格节点新场源下的亥姆霍兹方程结果相似。根据电磁互换原理,将原正演和观测点作为单位新场源正演求得的场值用在雅克比矩阵计算中;辅助场的雅克比矩阵是沿走向方向的场通过麦克斯韦方程的近似计算求得;视电阻率和视相位的雅克比项需要沿走向的场和辅助场的雅克比矩阵计算求得。文献[16]给出了MT反演中求取拉格朗日乘子的方法。
在大地电磁正演和雅克比矩阵计算采用Occam2DMT(v3.0)程序[17, 18]进行。
1.4 联合反演目标函数传统的联合反演目标函数包含对最小二乘数据的拟合和平滑约束,平滑约束帮助克服了非唯一解问题和不稳定问题。不同的是本文增加了交叉梯度算法,该算法在每次反演迭代中,地震波速度的更新需使目标函数的数据拟合和正则化项最小化,且下次反演迭代中电阻率模型的更新需兼顾上次反演迭代中生成的地震波速度模型,直到满足期望的拟合差。目标函数由数据拟合差和模型方差组成。定义目标函数为
约束条件为
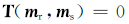
其中:d表示观测数据(dr为观测对数视电阻率,ds为观测地震旅行时间);fr(mr)为MT正演模型响应;fs(ms)是地震正演模型响应;C-1rr为电阻率观测数据的协方差;C-1ss为速度观测数据的协方差; C-1m为模型协方差矩阵;m0r和m0s为先验模型参数向量;β为辅助阻尼因子。
首先,通过泰勒级数展开法处理模型正演响应和约束条件可得
其中:k为迭代次数;Ar和As分别为fr和fs的雅克比矩阵;B为交叉梯度函数的导数,在二维情况下,可通过离散化求得:
然后,将式(7)代入到式(6)可得
约束条件为

其中:
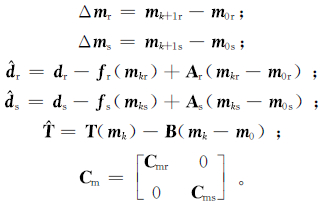
其次,利用拉格朗日乘子方法,将约束条件加入到目标函数中可得
其中,Λ为拉格朗日算子。
对式(10)求导乘以1/2得
式中,mi为第i个单元的模型参数。
最后,在约束条件下由式(11)=0,可得
将式(12)代入式(11)中可得
通过上述过程可求得目标函数结果。
1.5 程序流程交叉梯度联合反演主要通过两个循环完成:内循环和外循环。外循环主要进行地震初至波走时和MT的正演、雅克比矩阵的计算,并在给定的一个较大的β初始值下逐渐减小,进行数据拟合,得到最小二乘模型。内部循环进行交叉梯度约束的联合反演,主要计算拉格朗日算子,得到模型更新量,并对反演后的模型相似度进行判定,判断模型是否达到拟合程度,最终得到反演模型(图 2)。
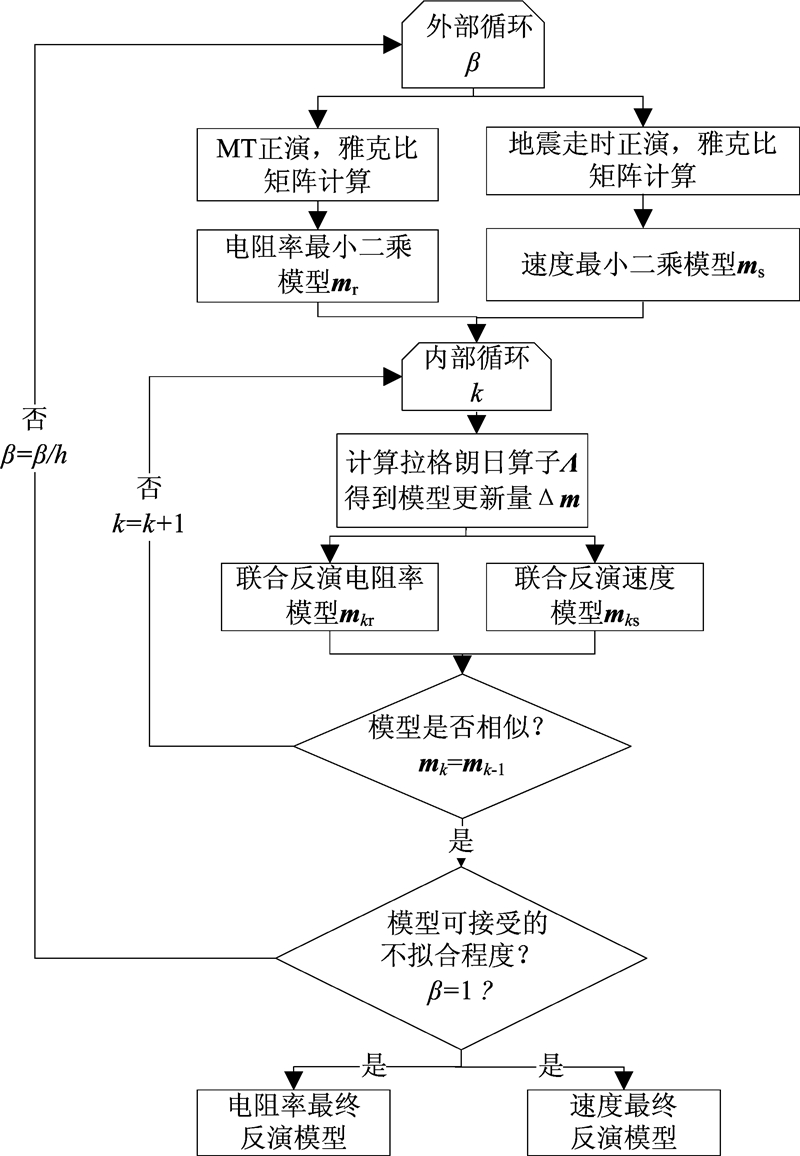 |
| 图 2 交叉梯度联合反演算法 Fig. 2 Algorithm of the crossgradient joint inversion |
| |
本文设计了2个理论模型,模型一如图 3所示。在MT电阻率模型(图 3a)中:左侧低阻异常体电阻率为1×101.5 Ω·m,其顶部和底部分别位于地下0.3和0.7 km;右侧高阻高速异常体电阻率为1×104 Ω·m,其顶部和底部分别位于地下0.3和1.2 km;均匀半空间背景场电阻率为1×102.5 Ω·m。在地震速度模型(图 3b)中:左侧为低速异常体,速度为3 000 m/s;右侧为高速异常体,速度为6 000 m/s ;均匀半空间背景场速度为4 000 m/s。MT电阻率模型和地震速度模型采用相同的均匀网格化,水平节点125个,垂直节点61个,网格节点间距为50 m。MT电阻率模型观测点为7个,间距为1 km,分布于地表;频率为1~1 000 Hz,共10个频率(对数间隔)。地震速度模型为地表放炮,共7个炮点,炮间距为1 km,检波器间距为0.2 km,位于两口井中,水平位置分别为1.5,4.5 km,每口井内有10个检波器。
 |
| R为电阻率;vP为纵波速度。 图 3 MT电阻率(a)和地震速度(b)理论模型一 Fig. 3 MT resistivity (a)and seismic velocity (b)theory model 1 |
| |
模型一反演结果如图 4所示,其中MT和地震两者的初始模型均为图 3理论模型中没有异常体的背景场。由图 4a、b可见,单独反演结果可确定异常体大概的位置,但反演异常体的准确值效果明显一般,并且几何形态也与真实的异常体(图中白框所示)差别很大。而且,图 4b中高速体周围产生的异常明显,且深部异常体明显差于浅层异常体的反演效果,深部反演出的异常体真实值较差。这是由射线均集中到模型的上边中心部分,走时数据对模型的两边和底部不敏感所致(图 5)。由图 4c、d可见,交叉梯度联合反演明显优于单独反演,反演出的异常体几何形态更接近真实异常体,反演出的异常体值与真实值很相似,并且地震深部的反演效果得到了提高。
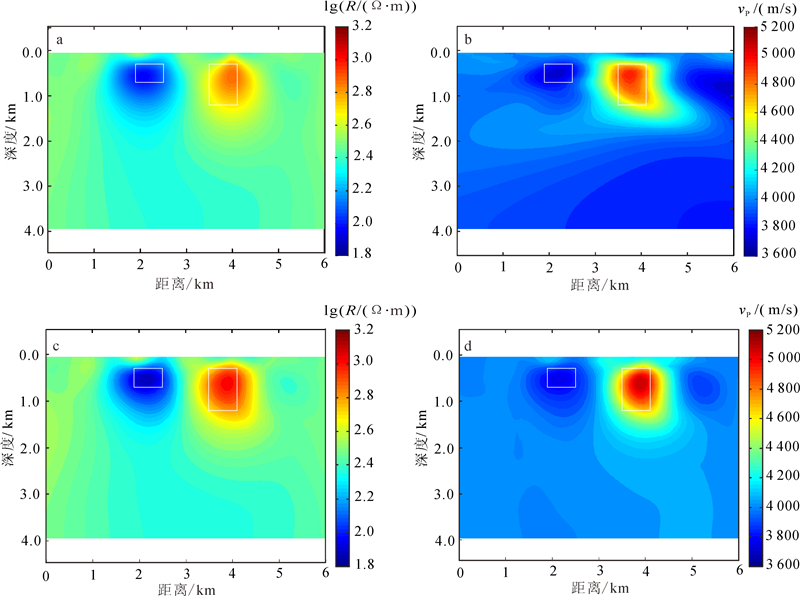 |
| 图 4 模型一单独反演(a、b)和联合反演(c、d)结果 Fig. 4 Separate inversion (a、b) and joint inversion (c、d) in model 1 |
| |
 |
| 图 5 模型一地震速度射线分布 Fig. 5 Distribution of rays in seismic velocity in model 1 |
| |
模型一联合反演和单独反演的速度和电阻率交叉梯度值如图 6所示。由图 6可见,联合反演远小于单独反演的交叉梯度值,表明联合反演后速度模型和电阻率模型的结构相似度较高。模型一电阻率和速度的交绘图如图 7所示。由图 7可见,联合反演推断的物性间相互关系比单独反演明显。
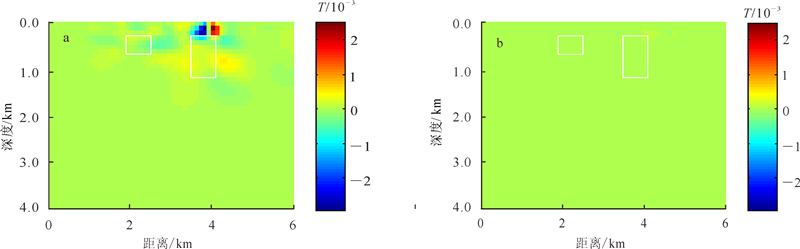 |
| 图 6 模型一单独反演(a)和联合反演(b)的电阻率和速度交叉梯度值 Fig. 6 Cross-gradients values of separate inversion (a) and joint inversion (b) of resistivity and seismic velocity in model 1 |
| |
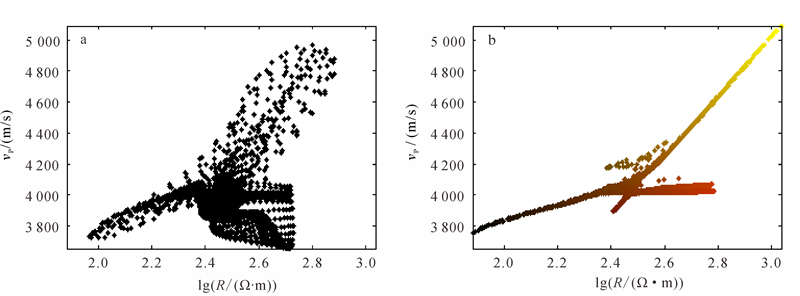 |
| 图 7 模型一单独反演(a)和联合反演(b)电阻率、速度交绘图 Fig. 7 Crossplots of separate inversion (a) and joint inversion (b) resistivity and seismic velocity in model 1 |
| |
模型二中的异常体具有相同的速度和不同的电阻率,如图 8所示。在MT电阻率模型(图 8a)中,异常体为2个大小相同的长方形板块体,电阻率分别为1×105 Ω·m和10 Ω·m,背景场电阻率为1×103.5 Ω· m,顶部和底部距地表分别为2.5 km和9 km;地表分布了间距为9 km的9个观测测点;频率为0.01~300 Hz,共8个频率(对数间隔)。在地震速度模型(图 8b)中,背景场速度为4 000~5 700 m/s,从地表逐层递增,异常体为2个相同的长方形板块体,速度均为6 000 m/s;共10个地震炮点置于地下0.5 km处,49个间距为2 km的检波器位于地表。模型二中2个模型采用相同的均匀网格化,水平节点205个,垂直节点51个,网格节点间距500 m。
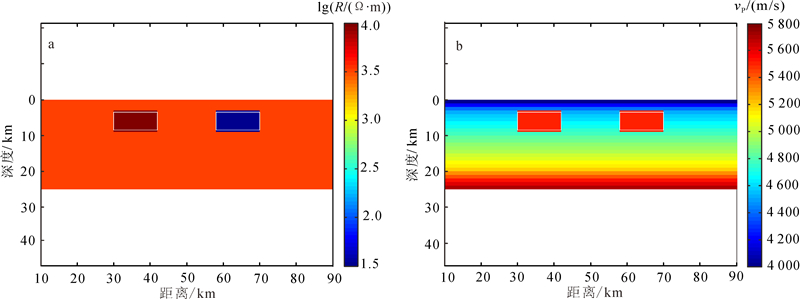 |
| 图 8 MT电阻率(a)和地震速度(b)理论模型二 Fig. 8 MT resistivity (a) and seismic velocity (b) theory model 2 |
| |
模型二反演结果如图 9所示,其中MT、地震初始模型均为没有异常体的背景场。由图 9a可见,MT电阻率单独反演结果在物性参数和几何形态上均与实际结果有偏差,且在异常体之间和周围围岩中出现假异常体的现象较严重。图 9b可见,深部异常体明显差于浅层异常体的反演效果,在速度单独深部反演出的异常体真实值较差。这是由于射线均集中至模型的上边中心部分,走时数据对模型的底部不敏感所致,如图 10所示。由图 9c和d可知,交叉梯度联合反演明显优于单独反演效果,如恢复异常体的几何形态和物性参数,并对地震深部的异常进行恢复。
 |
| 图 9 模型二单独反演(a、b)和联合反演(c、d)结果 Fig. 9 Separate inversion (a、b) and joint inversion (c、d) in model 2 |
| |
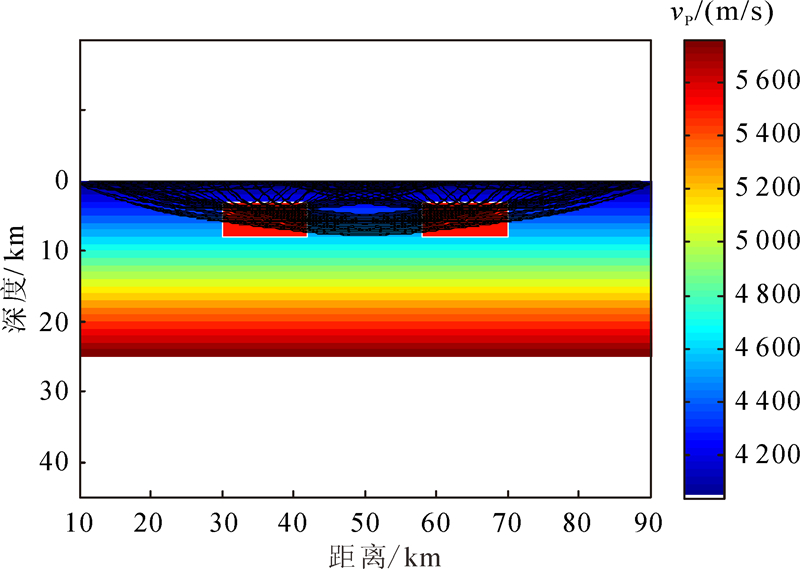 |
| 图 10 模型二地震速度射线分布 Fig. 10 Distribution of rays in seismic velocity in model 2 |
| |
模型二中单独反演和联合反演的电阻率和速度交叉梯度值如图 11所示。由图 11可见,联合反演远小于单独反演的交叉梯度值,表明联合反演后不同物性模型的结构相似度更高。模型二中电阻率和速度的交叉绘图如图 12所示。由图 12可见,联合反演比单独反演推断物性间的相互关系更明显。
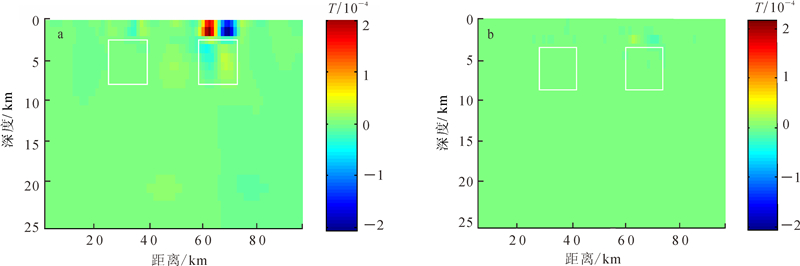 |
| 图 11 模型二单独反演(a)和联合反演(b)的电阻率和速度交叉梯度值 Fig. 11 Cross-gradients values of separate inversion (a) and joint inversion (b) of resistivity and seismic velocity in model 2 |
| |
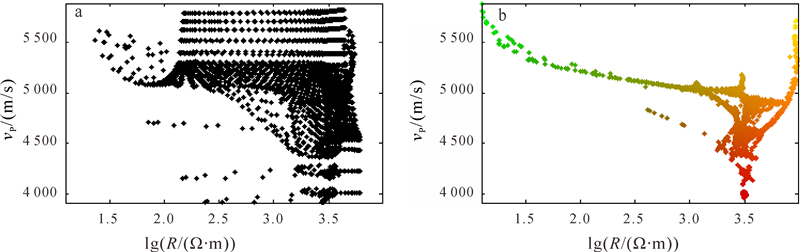 |
| 图 12 模型二单独反演(a)和联合反演(b)电阻率、速度交绘图 Fig. 12 Crossplots of separate inversion (a) and joint inversion (b) resistivity and seismic velocity in model 2 |
| |
综上,笔者研究了交叉梯度的基本理论,建立了2个模型,通过模拟实验分别得到单独反演和联合反演结果,从而证明了交叉梯度适合应用于联合反演中,可较好地改善单独反演的几何形态和物性参数。由2个模型实验对比可知,电阻率和速度不是同向变化的异常体,但通过交叉梯度联合反演可同时改善大地电磁和地震走时的单独反演结果;表明交叉梯度联合反演与岩石物性无关,仅取决于地下结构相似性。我们还可以通过联合反演的交叉绘图得到不同物性参数间关系,进一步证明了地下地质体中,不同物性具有一定的关系。将交叉梯度联合反演方法应用于地球物理勘探中,可以更好地解决非唯一解问题和更准确地寻找地下目标体。
不足之处在于本文采用的是规则网格,在反演效果上差于不规则网格,希望在以后研究中解决上述问题。
| [1] | 杨辉,戴世坤,宋海斌,等.综合地球物理联合反演综述[J].地球物理学进展,2002,17(2):262-271. Yang Hui, Dai Shikun, Song Haibin, et al. Integrated Geophysical Joint Inversion Review[J]. Progress in Geophysics, 2002, 17(2): 262-271. |
| [2] | 于鹏,王家林,吴健生,等.地球物理联合反演的研究现状和分析[J].勘探地球物理进展,2006,29(2):87-93. Yu Peng, Wang Jialin, Wu Jiansheng, et al. Research Status and Analysis of Joint Inversion[J]. Progress in Exploration Geophysics,2006,29(2):87-93. |
| [3] | Heincke B, Hobbs R. Joint Inversion of MT, Gravity and Seismic Data Applied to Sub-Basalt Imaging[C]//Annual Meeting. New Orleans: SEG, 2006: 784-787. |
| [4] | Colombo D, Stefano M D. Geophysical Modeling via Simultaneous Joint Inversion of Seismic Gravity, and Electromagnetic Data: Application to Prestack Depth Imaging[J]. The Leading Edge, 2007, 26(3): 326-331. |
| [5] | Haber E, Oldenburg D. Joint Inversion: A Structural Approach Inverse Problems[J]. IOP Science, 1997, 13: 63-77. |
| [6] | Zhang J, Morgan F D. Joint Seismic and Electrical Tomography[C]// Symposium on the Application of Geophysics to Engineering and Environmental Problems. [S.l.]: SEG,1997: 391-396. |
| [7] | Gallardo L A, Meju M A. Characterization of Heterogeneous Near-Surface Materials by Joint 2D Inversion of DC Resistivity and Seismic Data[J]. Geophysical Research Letters, 2003, 30(13): 1658-1661. |
| [8] | 彭淼,谭捍东,姜枚,等.基于交叉梯度耦合的大地电磁与地震走时资料三维联合反演[J].地球物理学报,2013,56(8):2728-2738. Peng Miao, Tan Handong, Jiang Mei, et al. Three-Dimension Joint Inversion Magnetotelluric and Seismic Travel Time Data with Cross-Gradient Constraints[J]. Chinese Journal of Geophysics, 2013, 56(8):2728-2738. |
| [9] | 王俊,孟小红,陈朝曦,等.交叉梯度理论及其在地球物理联合反演中的应用[J].地球物理学进展,2013, 28(4):2094-2103. Wang Jun, Meng Xiaohong, Chen Zhaoxi, et al. The Theory of Cross-Gradient and Its Application in Geophysical Joint Inversion[J]. Progress in Geophysics, 2013, 28(4):2094-2103. |
| [10] | Gallardo L A, Meju M A. Joint Two-Dimensional DC Resistivity and Seismic Travel Time Inversion with Cross-Gradients Constraints[J]. Jouranl of Geophsical Research, 2004, 109: 3311. |
| [11] | Vidale J. Finite-Difference Calculation of Travel-Ti-mes in Three Dimenisons[J]. Geophysics, 1990, 55: 521-526. |
| [12] | Zelt C A, Barton P J. Three-Dimensional Seismic Refraction Tomography: A Comparison of Two Methods Applied to Data from the Faeroe Basin[J]. Geophys Res, 1998, 103: 7187-7210. |
| [13] | 刘小军,王家林,于鹏,等.基于二次场的二维大地电磁有限元法数值模拟[J].同济大学学报:自然科学版,2007,35(8):1113-1117. Liu Xiaojun, Wang Jialin, Yu Peng, et al. Numerical Simulation of Two-Dimensional Magnetotelluric Secondary Field Based on the Finite Element Method[J]. Journal of Tongji University:Natural Science, 2007, 35 (8):1113-1117. |
| [14] | Wannamaker P E, Stodt J A, Rijo L. A Stable Finite Element Solution for Two-Dimensional Magnetotelluric Modeling[J]. Geophys J R,1987, 88: 277-296. |
| [15] | de Lugao P P, Wannamaker P E. Calculating the Two-Dimensional Magnetotlluric Jacobian in Finite Elements Using ReciProcity[J]. Geophys J,1996, 127: 806-810. |
| [16] | 朴英哲,李桐林,刘永亮,等.在大地电磁二维Occam反演中求取拉格朗日算子方法的改进[J].吉林大学学报:地球科学版,2014,44(2):660-667. Pak Yongchol, Li Tonglin, Liu Yongliang, et al. Improvement of Choosing Lagrange Multiplier on MT 2D Occam Inversion[J]. Journal of Jilin University : Earth Science Edition, 2014, 44(2): 660-667. |
| [17] | de Groot-Hedlin C D, Constable S C. Occam's Inversion to Generate Smooth, Two-Dimensional Models from MagnetotelluricData[J]. Geophysics, 1990, 93: 1613-1624. |
| [18] | Constable S C, Parker K L, Constable C G. Occam's Inversion a Practical Algorithm for Generating Smooth Models from EM Sounding Data[J]. Geophysics,1987, 52: 289-300. |