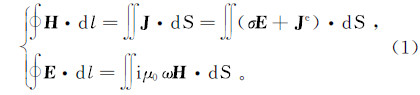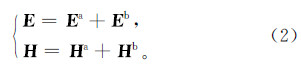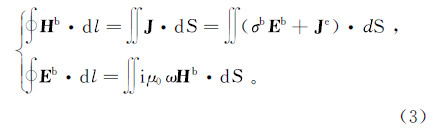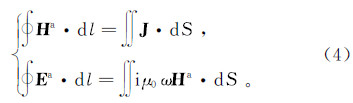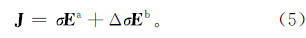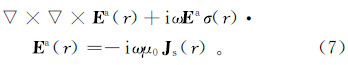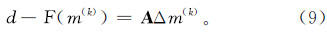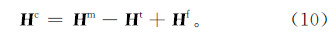2. 吉林大学地球探测与信息技术学院, 长春 130026
2. College of GeoExploration Science and Technology, Jilin University, Changchun 130026, China
0 引言
目前,航空电磁法地形校正还处于探索阶段,主要原因是航空电磁法探测数据量大,需要很高的计算速度和很大的内存才能完成。随着计算机技术的发展,对航空电磁法重点探测区域进行地形校正已逐步成为可能,有利于对重点成矿地区进行精细解释,提高解释效果。在国际上,Liu等[1]采用边界元的方法评价了地形对直升机航空电磁法的测量影响,认为在平缓起伏地形的测量中,地形产生的电磁响应影响达到10%左右;Newman等[2]采用3D有限元方法模拟二维地形条件下直升机航空电磁测量的响应,由于采用简单的地形而提高了计算的效率;Sasaki等[3]在总结前人研究的基础上,采用有限差分方法对二维地形电磁响应进行了模拟,模拟结果表明,在高地形或低地形上分别产生高阻和低阻异常,并提出了基于电磁响应的地形校正方法和带地形的反演方法等,提高了直升机航空电磁法的解释精度。目前国内还没有航空电磁法地形影响和校正方法研究的报道,但在地面电法中的地形影响处理方法已经得到一定程度的应用,取得了较好的效果,并成为一种实用技术。如阮百尧等[4]对大地电磁的二维地形影响进行了研究,研究结果表明,二维地形对Hx电磁波的影响十分严重,对Ex电磁波的影响却很小;徐世浙等[5]用边界单元法研究过同一问题,得到了同相的结论,即愈陡峭的倾斜地形,其观测值与区域值的均方相对偏差也愈大,而且随倾角的加大,倾斜地形影响急剧上升;徐世浙[6]用边界元法计算大地电磁Hx电磁波二维地形影响,并用有限元法计算了起伏地形水平层介质的大地电磁响应,用边界元法的结果对畸变后的大地电磁响应进行了地形改正,基本恢复了水平地形条件下层状介质的大地电磁响应,并最后给出了物理意义明确、形式简单的视电阻率和阻抗相位的地形改正公式;同年,徐世浙等[7, 8]又用边界单元法,发展了三维地形影响的改正方法研究,边界元法可以降低数值模拟的空间维数,具有解算位场问题所需要的方程组维数低、数据量少、计算速度快、精度高等优点,因此,该方法拟合地形能达到比较高的精度,是电阻率法点源二维、三维地形改正的一种实用的、有效的方法[9]。这些算法为航空电磁法的地形影响与改正方法研究提供了基础。
吊舱式直升机频率域电磁系统利用直升机拖吊电磁探头飞行测量,安装有偶极线圈装置的电磁探头在飞行过程中发射一次场,并接收大地中的二次场。根据电磁激发和感应原理分析感应电流分布规律方法分析,认为电磁线圈偶极装置在山坡上受地形的影响较小,而在山谷和山脊地形区域对感应电流分布影响较大,增加了异常的复杂程度;另外,直升机航空电磁系统在山区飞行作业,由于地形起伏变化较大,往往很难保持稳定的电磁探头飞行高度,而飞行高度的变化对电磁响应的影响较大。因此,研究复杂地形对电磁偶极场的影响程度,以及如何准确提取由于地形产生的电磁场,对于提高直升机频率域航空电磁法的解释精度具有一定的现实意义。 1 复杂地形频率域航空电磁响应计算方法
航空电磁法地形影响及校正方法研究,根据实际情况主要采用一维、二维和三维方法。一维方法主要是将地形产生的电磁响应以一维的形式补偿到实测数据中,以便实现地形的简单校正,这种方法在测量区域较大且地形起伏较小时具有较好的效果,但在地形起伏较大的区域应用效果受到限制。二维校正方法实际上是将地形简化为二维的形式,计算二维地形的电磁响应,并在二维的基础上进行地形数据校正。由于三维方法计算数据量较大,目前主要应用在范围不大的区域进行地形数据校正。
电磁数值计算方法主要包括有限差分法、有限元法和积分方程法[10, 11]。其中积分方程法因只需对有限大小的异常体进行离散,对层状介质中三维有限大小异常体的模拟速度快而被广泛关注,但对复杂模型模拟的不适应性使得该方法没有被广泛应用。有限元法和有限差分法被认为比积分方程法更适合模拟任意复杂模型[12, 13, 14, 15, 16],但这两种算法都需对全空间离散,对计算机资源要求很高。随着计算机技术的发展,国际上已开始采用二维和三维有限差分方法模拟二维或三维地形条件下的直升机航空电磁响应和进行地形校正方法研究[17, 18, 19],并取得了好的应用效果。频率域航空电磁系统的工作方式是采用独立发射的多种装置、多频率分量进行观测,因此采用频率域有限差分方法可以模拟接近实际的频率域航空电磁系统工作方式,并对每次单独发射的固定频率信号进行模拟。
频率域航空电磁法工作频率范围为870~23 250 Hz,可以忽略位移电流,同时地下介质的磁导率μ近似等于真空中的磁导率μ0。设电磁场随时间变化的因子为exp(iωt),则麦克斯韦方程组的积分表达式为
式中:E为电场强度矢量;H为磁场强度矢量;ω为圆频率;σ为介质的电导率;J为电流密度;Je为位移电流密度;t为时间;l为长度;S为面积。麦克斯韦方程组离散化后得到的线性方程组是相同的。通常的方式将总场分解为背景场(一次场)和感应场(二次场),背景场(一次场)利用快速汉克尔变换求取,感应场(二次场)采用数值计算求解。将总场表示为一次场和二次场的和: 式中:Ea和Eb分别为二次场和背景场的电场强度;Ha和Hb分别为二次场和背景场的磁场强度。经过总场分离后,背景场满足的麦克斯韦方程积分形式为 式中:σb为背景场介质的电导率。将总场所满足的麦克斯韦方程(1)减去背景场所满足的麦克斯韦方程(3),即得到二次场满足麦克斯韦方程的积分形式:
其中:J与Ea、Eb和电导率的关系为 式中,Δσ为剩余电导率: 把公式(4)写成微分形式,即 式中:r为空间距离;Js为面电流密度。利用交错网格有限差分方法可以求解(7)。先将式(7)中的旋度公式表示为偏微分的格式,然后将偏微分按照图 1所示的交错差分方法离散。
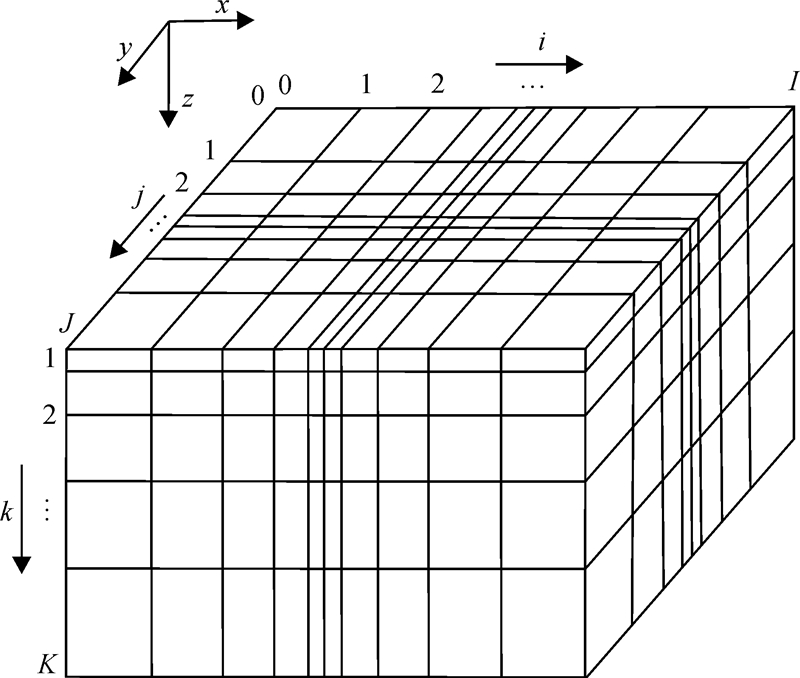 |
| 图 1 Yee非均匀网格剖分示意图Fig. 1 Schematic plot for Yee non-uniform grid generation |
经过上述变换后,频率域航空电磁数值模拟问题即转化为背景场和二次场的求解,背景场可以通过快速汉克尔变换求解,二次场采用三维交错采样有限差分法进行数值计算[20]。将得到的背景场值加上二次场值即为磁偶源激发下的三维频率域航空电磁场分布。在有限差分网格剖分方面,采用非均匀变化交错网格[21, 22],这样可以在满足计算精度的前提下尽量扩大模型尺寸,达到更好的应用效果(图 1)。
2 频率域航空电磁法地形响应校正算法
航空电磁法在测量过程中,不仅可以获得不同频率的实、虚分量数据,而且还可以获得测区所有点的飞行高度[23]和数字地形图,这为研究和消除由于地形起伏原因引起的电磁影响创造了条件。即可以采用不同测点的飞行高度和地形,在电阻率反演的基础上,计算由于飞行高度和地形变化所产生的电磁响应。
在进行电磁场的计算时,首先利用频率域有限差分实现2.5维电磁场的计算,这种方法可以模拟比较复杂的地质断面,对比较复杂的起伏地形模拟计算非常实用。通过理论模型的计算,可以分析计算结果的稳定性和可靠性,并分析不同地形对频率域航空电磁法的影响程度,以及研究消除地形影响的算法和方法。其次进行3维电磁场的计算,3维地质体的航空电磁响应计算可以更加精确地分析地形影响和地质体的电磁响应,可以提高对复杂形态地质体或重点异常的解释精度。具体计算内容包括:
1)在2D条件下,且地形起伏较小的情况下,沿水平面测量情况下的地形影响;
2)在2D条件下,且地形起伏较大的情况下,沿起伏地形测量情况下的地形影响;
3)在3D条件下,且地形起伏较小的情况下,沿水平面测量情况下的地形影响;
4)在3D条件下,且地形起伏较大的情况下,沿起伏地形测量情况下的地形影响。
在以上4种地形计算模型的条件下,可以分析不同飞行高度、不同地下介质电性、不同地形起伏大小与电磁响应的关系。
在2.5维和3维的电磁响应计算中,根据介质的物性参数随频率变化的模型如Cole-Cole模型或Debye模型,计算多频航空电磁测量情况下的介质电磁响应。具体步骤包括:
1)根据航空电磁法在实际测量过程中获得的地理位置和高程数据,建立地形计算模型和确定网格划分方法。
2)根据半空间模型,采用频率域航空电磁法反演方法对实测数据进行电阻率计算,并采用线性统计的方法将其均匀化的电阻率作为大地介质的背景电阻率,并根据实测数据中记录的高程数据,建立由任意实测高程数据生成的、以反演视电阻率为背景的均匀大地背景计算模型。然后取区域电阻率的平均值,代入1)模型中的每个网格,根据频率域有限差分方法计算纯地形的影响。同时计算局部介质电阻率由于地形的起伏产生的电磁响应。
3)在获得由于地形和局部地质体的电磁响应后,将分析能够消除电磁响应中地形影响的方法。但在上述计算过程中,地形体的电阻率值是根据具有地形影响下的电磁响应获得的,其中必然还存在一定的误差,而且将起伏地形转化为水平地形时也有误差。因此需要采用精确的方法来消除目标体由于起伏地形转化为水平地形时的影响。上述方法获得地形改正的结果可以作为初步的结果,其优点是计算效率较高,可用于大面积数据处理和解释。
4)如果局部区域需要提高地形改正结果的精度,可采用迭代高斯-牛顿方法。电磁响应可表示为
式中:d为测量的电磁响应;m为模型参数,其中包括电阻率的分布;F为正演模型函数,其中包括地形的水平化。求解该问题,采用线性近似的迭代高斯-牛顿方法,即可以表示为 式中:m(k)是第k次模型迭代值;Δm(k)是模型的修改值;A是正演函数F的雅克比矩阵。收集航空电磁法测量区域可能涉及的地下介质参数的变化范围,以及不同飞行高度、不同工作频率下均匀半空间模型二次场与介质参数、高度、频率的关系,并形成关系数据表。该数据表可作为数据预处理中高度变换及高度校正的理论依据。以下是地形改正的表达式:
式中:Hc是校正后的电磁异常响应;Hm是测量电磁数据;Ht是均匀的具有地形起伏时的电磁响应;Hf是地表水平时的电磁响应。在地形校正中,根据航空电磁测量数据反演方法所获得的电阻率结果计算平均值或局部平均值,以该平均值为电性参数,计算水平均匀半空间和起伏地形的电磁响应,起伏地形与均匀半空间的电磁响应之差即为由地形引起的电磁响应,以该差值进行地形补偿校正。
根据地形校正量,以及区域已知目标的探测结果,来分析地形校正的准确程度,然后修改模型的电磁参数,进行迭代计算,直到满足要求为止(图 2)。
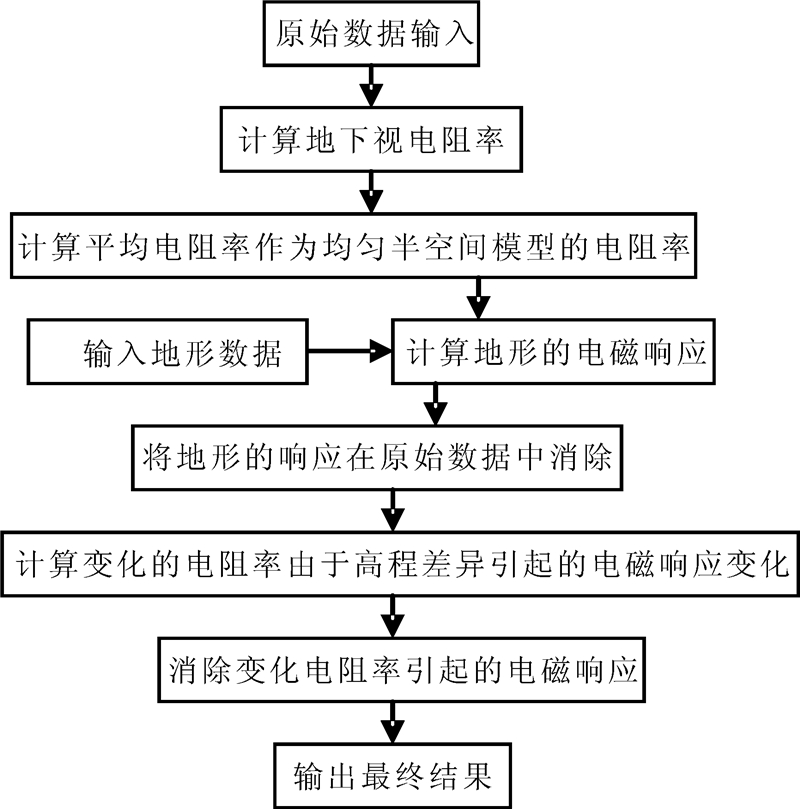 |
| 图 2 地形电磁响应计算和分析框图Fig. 2 Diagram of calculation and analysis of topographic electromagnetic response |
频率域航空电磁响应二维算法比三维计算速度快,便于快速分析频率域航空电磁测量的地形影响程度,因此首先利用频率域有限差分方法计算频率域航空电磁法二维地形的电磁响应。
图 3a为纯凹地形模型(类似山沟),地下介质相对介电常数和相对磁导率设为1,电导率为0.002 S/m。图 3b为含有一个直立长方形低阻体的凹地形模型,其中介电常数、磁导率、 地下介质电导率与图 3a相同,直立长方形低阻体高200 m,宽100 m,电导率为0.1 S/m。电磁系统收发线圈测量高度为35 m,收发线圈间距为5 m。分别采用水平共面(HCP)和垂直同轴(VCX)两种线圈收发装置进行二维剖面电磁正演模拟。
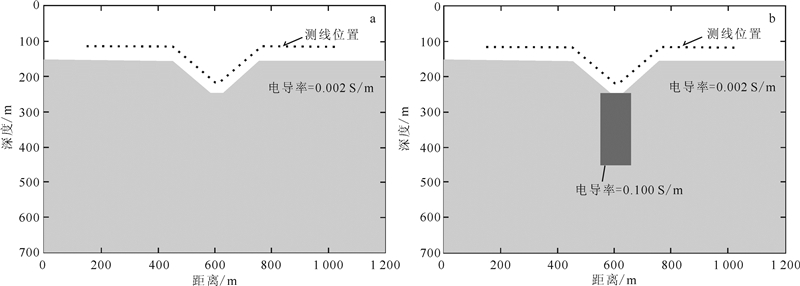 |
| a.纯凹地形模型;b. 含一个直立长方形低阻体的凹地形模型。 图 3 二维凹地形正演模型Fig. 3 Forward model of 2D concave relief |
由地形(图 3a)和地形加低阻目标体(图 3b)条件下的电磁响应曲线特征对比(图 4)可以看出:凹地形可以产生正的电磁异常,而且同轴装置受凹地形的影响程度大于共面装置,在凹地形的低点附近,同轴装置实分量由地形产生的电磁响应,甚至超过了良导体引起的异常幅度。如果凹地形介质中含有良导体,凹地形引起的电磁异常与良导体引起的电磁异常容易混淆,并增大了良导体引起的异常幅度,给异常解释带来很大的误差。
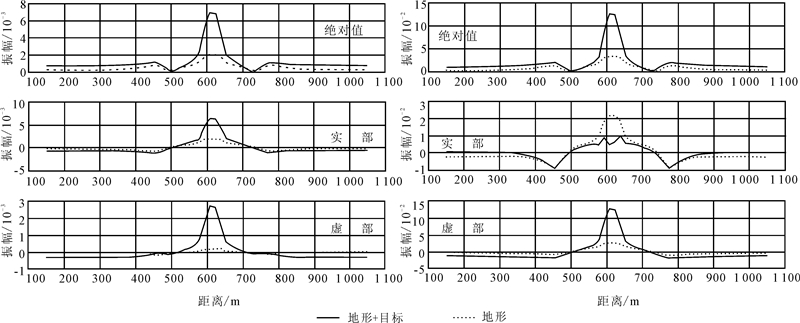 |
| 左图HCP, 23 25 0 Hz;右图VCX , 21 750 Hz。 图 4 二维凹地形电磁响应曲线特征Fig. 4 Electromagnetic response of 2D concave relief |
对凹地形加高阻或低阻目标体的电磁响应特征进行研究,结果(图 5)表明:含高阻体凹地形在校正前的实虚分量曲线表现为明显的升高电磁异常,而地形校正后的高阻体电磁异常表现为低缓的降低值电磁响应,说明升高的电磁异常主要由凹地形引起,地形影响基本掩盖了高阻体引起的异常,因此,在凹地形的低点位置,地形影响是非常大的。同理,右图含低阻体地形校正前的实虚分量曲线强度远远大于孤立低阻体引起的升高电磁异常,而地形校正后的低阻体电磁异常幅度明显变小,表现为低缓的升高电磁异常。由此可见,地形对目标体电磁异常影响较大,可使目标地质体电磁异常畸变,甚至表现为幅度相反的电磁异常特征。
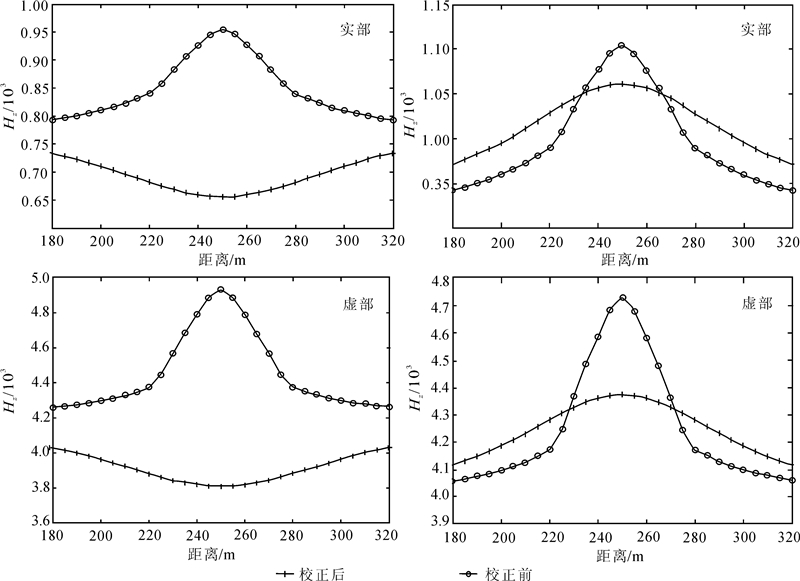 |
| 图 5 共面装置凹地形中高阻体(左)和低阻体(右)电磁响应特征及校正结果Fig. 5 Response and correction results of resistive object (left) and conductive object (right) below the concave relief |
4.1 不同坡度起伏模型的电磁响应特征
为了研究地形起伏程度对频率域航空电磁响应的影响,设计如图 6所示的台阶模型,台阶坡角分别为0°,9°,18°,26°,33°,地下介质电导率为0.01 S/m,电磁收发线圈离地高度35 m。通过对两种收发线圈装置的电磁响应进行模拟计算,分析不同电磁收发线圈装置在此种地形模型条件下对电磁响应的影响程度。
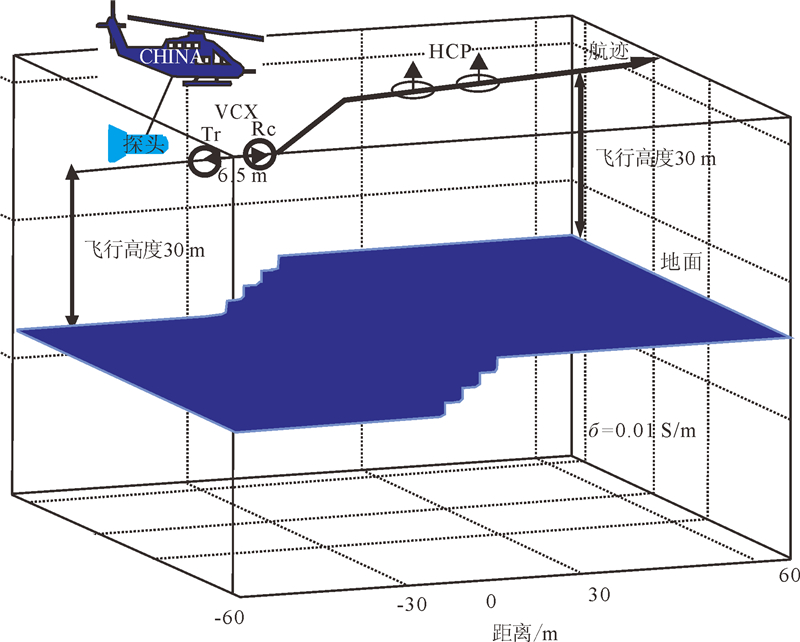 |
| Tr.发射线圈;Rc.接收线圈。 图 6 不同坡角台阶模型示意图Fig. 6 Different slope angle of stair-step model |
从图 7、8可以看出,不管是水平共面装置、还是垂直同轴装置,Hx、Hz的实、虚分量响应随着地形坡度角度的变化也存在明显的变化,地形起伏对各个装置的不同分量影响程度也不同,其中虚分量随地形坡角的变化较大。HCP装置随地形坡度的增大,电磁响应曲线变化较小,Hz实分量受地形影响最小;而VCX装置的Hx虚分量受地形影响最大,当坡角变化到33°时,与水平地形的电磁响应曲线相比,电磁响应差异可达20×10-6左右。由此可以看出,在频率域航空电磁法实际应用中,应注重分析地形对不同收发线圈装置的电磁响应曲线影响特点,以便采取合适的地形校正方法,尤其应注意对VCX装置虚分量采用合理的地形校正方法。
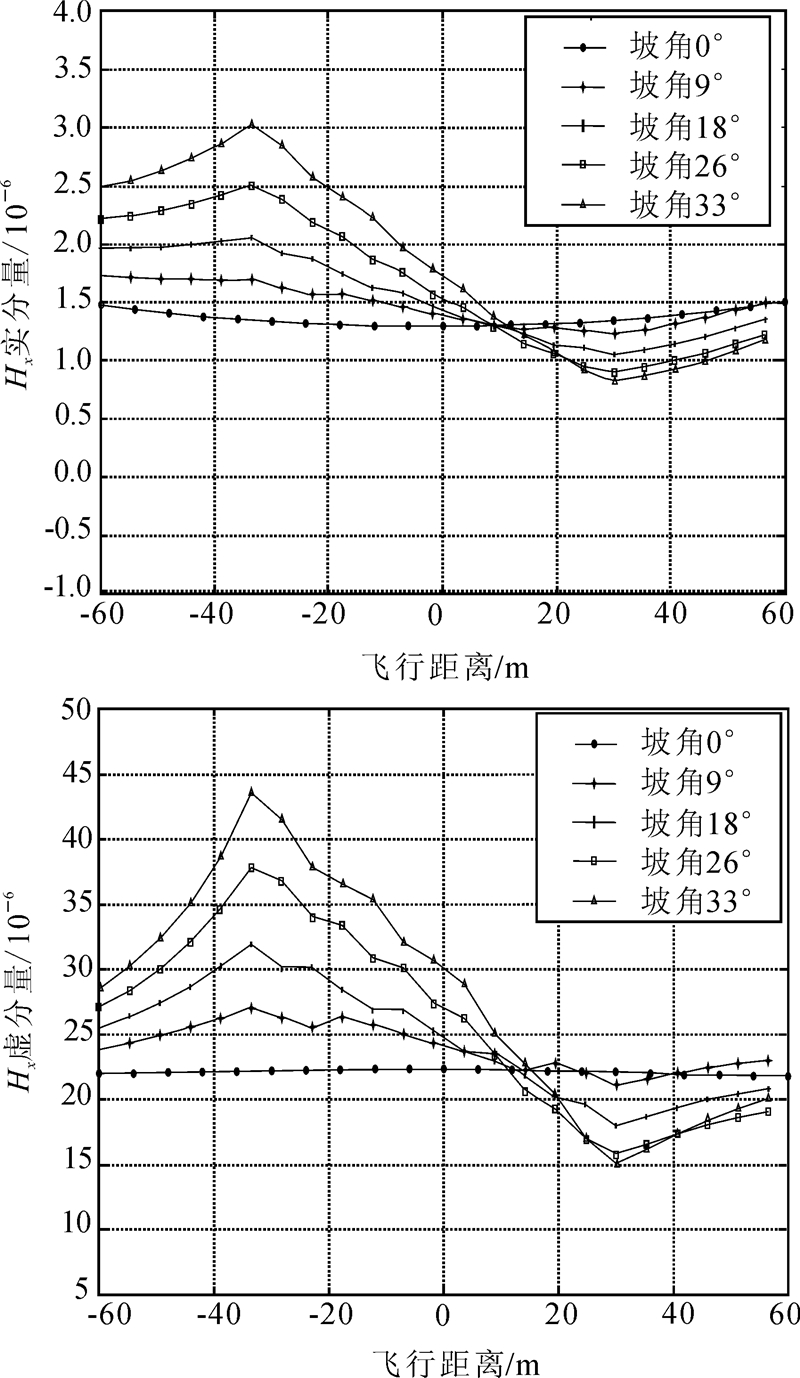 |
| 图 7 VCX装置Hx实虚分量在不同坡角变化条件下的电磁响应信号对比曲线Fig. 7 Contrast of vertical coaxial system electromagnetic response signal at different slope angle |
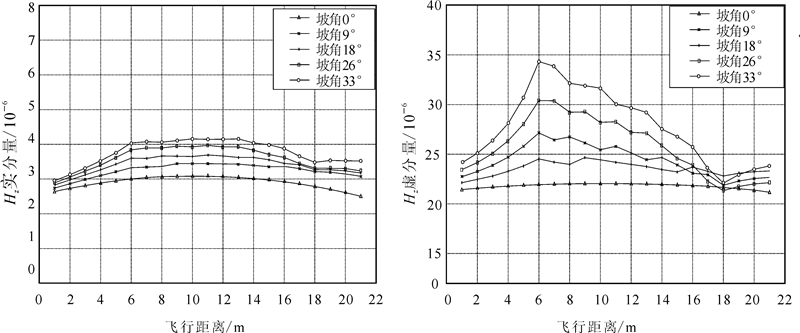 |
| 图 8 HCP装置Hz实、虚分量在不同坡角变化条件下的电磁响应信号对比曲线Fig. 8 Contrast of horizontal coplane system electromagnetic response signal at different slope angle |
在频率域航空电磁法实际飞行测量中,为了检查仪器的观测精度,经常开展某一测线同一方向和不同方向在同一高度的重复线测量。而对于同一起伏地形,当飞机沿不同方向飞行测量时,根据电磁偶极收发线圈的激发原理,相同地形、相同地电条件下不同飞行方向的电磁响应会存在一定的差异。如图 9所示的起伏阶梯模型,地下介质电导率为0.01 S/m,直立相对良导圆柱体电导率为0.03 S/m,电磁收发线圈离地高度35 m。由图 10中两种装置不同飞行方向的电磁响应曲线中可以看出,HCP和VCX装置不同飞行方向的电磁响应曲线,在此种地形起伏条件下存在一定差异,根据这一地形电磁响应特点,研究地形对不同飞行方向电磁响应的影响程度,可以提高实测航空电磁数据处理、地形校正,以及对航空电磁测量重复线的评价精度。
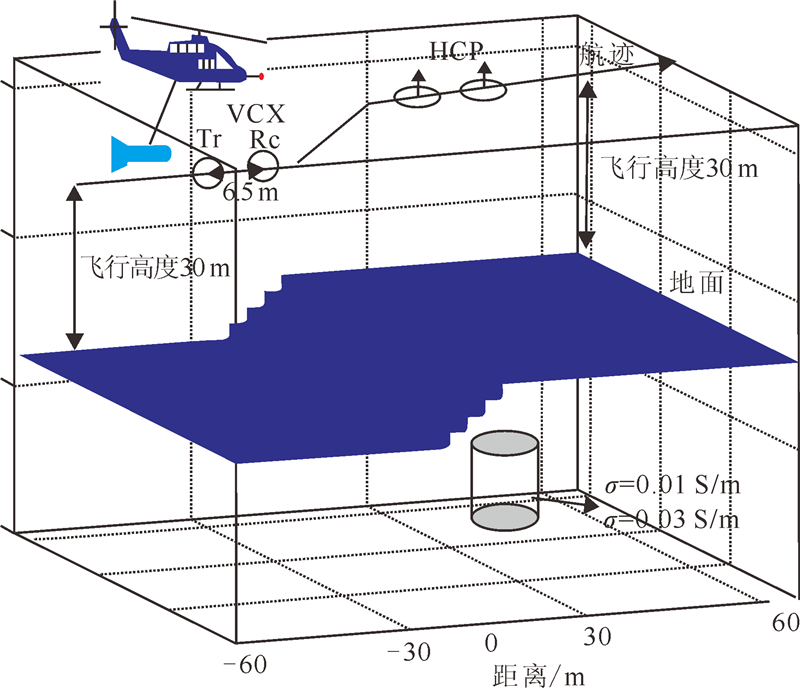 |
| 图 9 不同坡角起伏地形地电模型(含有良导直立圆柱体)不同飞行方向示意图Fig. 9 Different direction flight upon rugged topographic geoelectric model (the model contains a conductive vertical cylinder) with different slope angle |
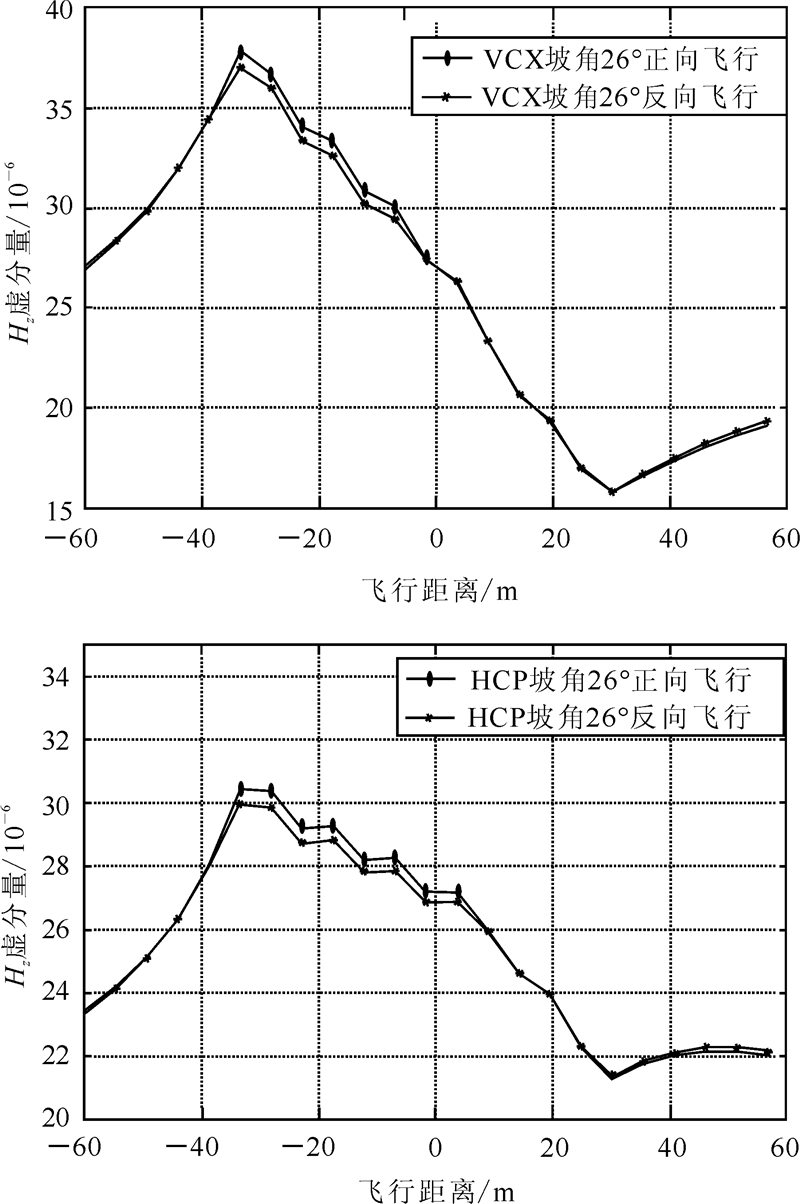 |
| 图 10 不同飞行方向两种装置电磁响应信号对比曲线Fig. 10 Electromagnetic response contract for the two systems with different flight direction |
以国内现有的吊舱式频率域直升机航空电磁系统为例,令两种收发线圈装置分别发射3个频率:水平共面装置发射频率930、4 650 、23 250 Hz,垂直同轴置发射频率870、4 350、21 750 Hz。设计模型如图 11所示的复杂起伏地形模型,采用三维频率域有限差分程序对该模型进行模拟计算。
 |
| 图 11 复杂起伏地形地电模型(含有良导直立圆柱体)示意图Fig. 11 Complex rugged topographic geoeletric model(the model contains a conductive vertical cylinder) |
在二维频率域有限差分地形校正研究中,由于采用二维模型模拟计算,边界反射对于目标信号会产生一定的干扰,而且二维算法在计算精度上也比三维低,因此,三维频率域有限差分计算复杂起伏地形的电磁响应和校正效果较好。计算结果如图 12所示。从同轴装置三个频率的二次磁场响应曲线(图 12左图)可以看出,频率越高受地形影响程度越大、目标体电磁响应曲线畸变越大,以至于根据电磁响应曲线特征无法区分目标体异常和地形起伏引起的异常,给解释工作带来困难。因此,对地形引起的异常进行校正是十分必要的。图 12右图是针对图 11所示模型的同轴收发装置21 750 Hz电磁响应和校正后的结果,可以看出:校正前电磁虚分量曲线呈多峰值,与孤立良导直立圆柱体的电磁响应特征不符,电磁异常受地形影响产生了严重畸变;而地形校正后曲线基本消除了因地形起伏引起的虚假异常,电磁虚分量呈单个峰值,基本上反应了孤立良导直立圆柱体的电磁响应特征。
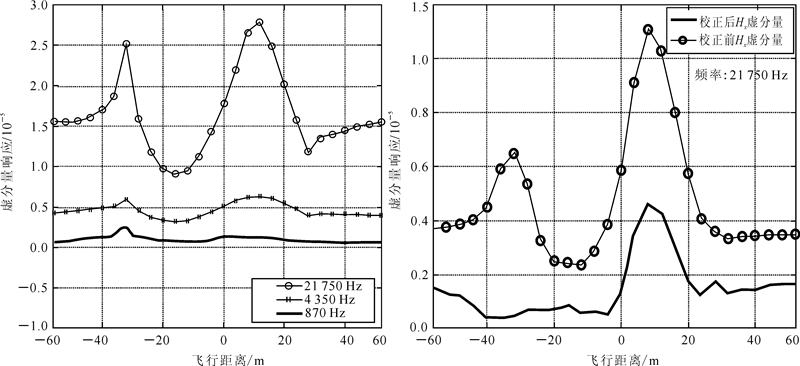 |
| 左图.同轴装置3个频率的虚分量;右图.21 750 Hz虚分量校正前后对比曲线。 图 12 垂直同轴装置在复杂起伏地形条件下的电磁响应及校正结果Fig. 12 Response and correction result of vertical coaxial system with complex rugged topography |
为了验证本次研制的地形校正方法的有效性,选取2003年11月在北京密云地区实测的10号线频率域航空电磁数据进行地形校正。图 13a是采用实测数据高程所生成的纯地形模型,数据测线长度为1 200 m,大地均匀介质视电阻率为55 Ω·m。图 13b为直升机航空电磁系统垂直同轴装置870 Hz虚分量的地形校正结果对比曲线。由图 13可看出:校正前实测的电磁响应数据与纯地形模型正演曲线特征曲线特征类似,反应了实测电磁数据明显受地形起伏高低的影响;而校正后的虚分量电磁曲线特征与地形无关,对实测数据中因地形引起的局部干扰起到了明显的压制作用,与地下介质地电特征相符。
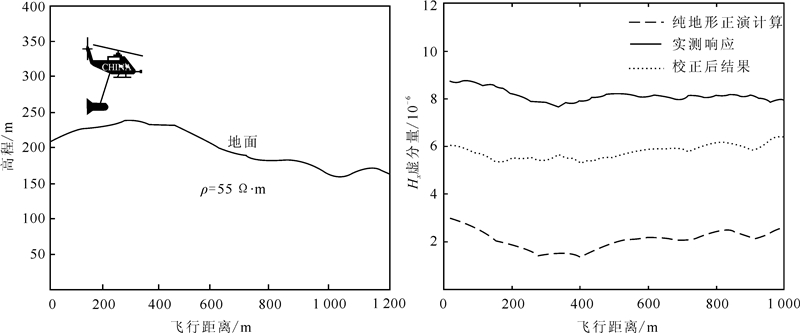 |
| a.北京密云地区实测高程数据正演计算模型;b.870 Hz虚分量地形校正结果对比曲线。 图 13 直升机航空电磁地形校正结果对比曲线Fig. 13 Contract of topographic correction for helicopter airborne electromagnetic method |
1)在充分调研国内外电磁法地形影响和数值模拟计算方法的基础上,推导出了二维和三维频率域航空电磁场的数值计算算法,实现了对二维、三维起伏地形的数值响应模拟计算。
2)选择典型频率域航空电磁数据模型进行地形影响和地形校正方法技术分析,通过研究分析认为地形对频率域航空电磁测量结果具有较大影响,特别是在地形局部变化较大的区域,如山顶、沟谷等部位地形影响最大。
3)建立了频率域航空电磁法地形校正的计算方法,通过二维和三维频率域航空电磁法地形校正方法对模型和实测数据进行校正,能够有效压制地形对电磁异常的影响,取得了好的应用效果。
| [1] | Liu G, Becker A. Evaluation of Terrain Effects in Aem Surveys Using the Boundary Element Method[J]. Geophysics, 1992, 57: 272-278. |
| [2] | Newman G A, Alumbaugh D L. Frequency-Domain Modelling of Airborne Electromagnetic Responses Using Staggered Finite Differences[J]. Geophys Prosp, 1995, 43: 1021-1042. |
| [3] | Sasaki Yutaka,Nakazato Hiroomi.Topographic Effects in Frequency-Domain Helicopter-Borne Electromagne-tics[J]. Exploration Geophysics, 2003, 34, 24-28. |
| [4] | 阮百尧,徐世浙,戴世坤,等. 二维大地电磁测深曲线的快速反演[J]. 桂林工学院学报, 1998,18(1): 53-56. Ruan Baiyao, Xu Shizhe, Dai Shikun,et al. Rapid Inversion of 2D Magnetotelluric Sounding Date[J]. Journal of Guilin Institute of Technology, 1998,18(1): 53-56. |
| [5] | 徐世浙,于涛. 电导率分块连续变换的二维MT有限元模拟[J]. 高校地质学报,1995,2(2): 65-73. Xu Shizhe, Yu Tao. The Finite Element Method for Modeling 2-D MT Field on a Geoelectrical Model with Continuous Variation of Conductivity Within Each Block[J]. Geological Journal of China Universities, 1995,2(2): 65-73. |
| [6] | 徐世浙. 电导率分层连续变化的水平层的大地电磁正演[J]. 地球物理学报,1995,38(2): 262-268. Xu Shizhe. A Numerical Method for Calculating MT Field on a Layered Model with Continuous Change of Conductivity in Each Layer[J]. Chinese Journal of Geophysics, 1995, 38(2): 262-268. |
| [7] | 徐世浙, 阮百尧, 周辉,等. 用边界元法模拟三维地形对MT场的影响[J]. 科学通报, 1996,41(23): 2162-2164. Xu Shizhe,Ruan Baiyao,Zhou Hui,et al. Modeling 3-D Terrain Effect on MT by the Boundary Element Method[J]. Chinese Science Bulletin, 1996, 41(23): 2162-2164. |
| [8] | 徐世浙,阮百尧,周辉,等. 大地电磁场三维地形影响的数值模拟[J]. 中国科学:D辑:地球科学, 1997, 27(1): 15-20. Xu Shizhe, Ruan Baiyao, Zhou Hui, et al. The Electromagnetic Field Numerical Simulation of Three-Dimensional Terrain Effect[J]. Science in China:Serious D:Earth Sciences, 1997, 27(1): 15-20. |
| [9] | 黄兰珍,田宪谟. 电阻率法地形改正及其在工程地质勘查中的应用[J]. 物探化探计算技术, 1997, 19(03):238-241. Huang Lanzhen, Tian Xianmo, Topographic Correction for Resistivity Method and Its Application to Engineering Geological Prospecting[J]. Computing Techniques for Giophysical and Geochenical Exploration, 1997, 19(03):238-241. |
| [10] | 戴世坤,徐世浙. MT二维和三维连续介质快速反演[J]. 石油地球物理勘探, 1997,32(3): 305-317. Dai Shikun, Xu Shizhe. MT 2-D and 3-D Continuum Rapid Inversion[J]. Oil Geophysical Prospecting, 1997, 32(3): 305-317. |
| [11] | 晋光文,赵国泽,徐常芳,等. 二维倾斜地形对大地电磁资料的影响与地形校正[J]. 地震地质,1998,20(04): 454-458. Jin Guangwen,Zhao Guoze,Xu Changfang,et al. The Affection and Oorrection on Magnetotelluric Response Data for Inclination Two-Dimension Terrainseismology and Geology[J]. Seismology and Geology, 1998,20(04): 454-458. |
| [12] | 熊盛青. 航空伽玛能谱异常解释中地形影响及校正方法研究[J]. 地学前缘, 1998,5 (2):341. Xiong Shengqing. Study of Topographic Influence and Correction Method in the Airborne Gamma Spectrum Anomaly Interpretation[J]. Earth Science Frontiers, 1998, 5(2): 341. |
| [13] | 范正国,于长春. 航空伽马能谱地形改正新方法及应用[J] 物探与化探, 2005,29(1): 28-33. Fan Zhengguo, Yu Changchun. The Application of Electric Logging Curve to Calculating Mineralization Degree of Formation Water Geophysical and Geochemical Exploration[J]. 2005,29(1): 28-33. |
| [14] | 何继善,任宝琳. 用样条函数插值的电阻率地形改正方法[J]. 地质与勘探, 1984,24(7):39-43. He Jishan,Ren Baolin. Resistivity Terrain Correction Method Using Spline Function Interpolation[J]. Geology and Prospecting,1984,24(7) :39-43. |
| [15] | 张宗岭. 自然电位地形改正探讨[J]. 地质与勘探, 1989, 25(11):28-42. Zhang Zongling. Topographic Correction for Natural Potential Method[J]. Geology and Prospecting, 1989, 25(11):28-42. |
| [16] | 周明平. 瞬变电磁法测量中地形改正方法探讨[J]. 贵州地质, 2004, 21(2):117-120. Zhou Mingping. A Discussion on the Landform Rectified Way in Themeasurement of Transient Electromagnetic Method[J]. Guizhou Geology, 2004, 21(2):117-120. |
| [17] | Mackie R L, Smith J T, Madden T R. Three-Dimensional Electromagnetic Modeling Using Finite Difference Equations[J]. The Magnetotelluric Example: Radio Science, 1994, 29: 923-935. |
| [18] | Sasaki Y. Full 3d Inversion of Electromagnetic Data on Pc[J]. Journal of Applied Geophysics, 2001, 46: 45-54. |
| [19] | Smith J T. Conservative Modeling of 3d Electromagnetic Fields: Part I: Biconjugate Gradient Solution and an Accelerator[J]. Geophysics, 1996, 61: 1319-1324. |
| [20] | 谭捍东, 余钦范, Booker J, 等. 大地电磁法三维交错采样有限差分数值模拟[J]. 地球物理学报, 2003, 46(5): 705-711. Tan Handong, Yu Qinfan, Booker J, et al. Magnetotelluric Three-Dimensional Modeling Using the Staggered-Grid Finite Difference Method[J]. Chinese Journal of Geophysics, 2003,46(5): 705-711. |
| [21] | 顾观文,吴文鹂,李桐林. 大地电磁场三维地形影响的矢量有限元数值模拟[J]. 吉林大学学报:地球科学版,2014,44(5):1678-1686. Gu Guanwen, Wu Wenli, Li Tonglin. Modeling for the Effect of Magnetotelluric 3D Topography Based on the Vector Finite-Element Method[J]. Journal of Jilin University: Earth Science Edition, 2014, 44(5):1678-1686. |
| [22] | 史明娟,徐世浙. 大地电磁二次函数插值的有限元法正演模拟[J]. 地球物理学报, 1997, 40(3) :421-430. Shi Mingjuan, Xu Shizhe. Fintte Element Method Using Quadratic Etement in MT Forward Modeling[J]. Chinese Journal of Geophysics, 1997, 40(3) :421-430. |
| [23] | 王卫平, 曾昭发. 基于磁导率的频率域航空电磁法双频反演方法[J]. 地质科技情报, 2013,32(2): 181-186. Wang Weiping, Zeng Zhaofa. Frequency Domain Airborne Electromagnetic Dual-Frequency Inversion Method Based on Magnetic Permeability[J]. Geological Science and Technology Information,2013,32(2): 181-186. |