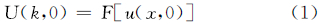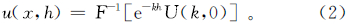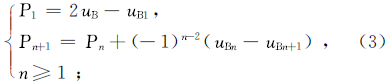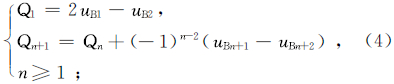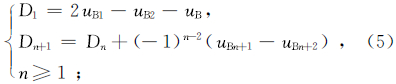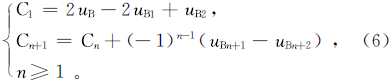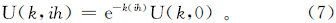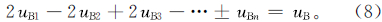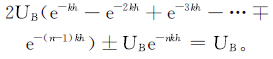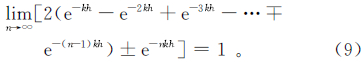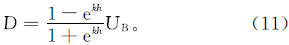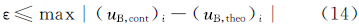0 引言
通过快速傅里叶变换(FFT)实现位场向下延拓是在重、磁资料处理中常用的方法,但向下延拓的不稳定性十分明显。频率域向下延拓一般只能向下延拓二三个资料点距。为了改善向下延拓的稳定性,提高延拓距离,许多地球物理学家提出了种种方法,包括改进的方法[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]。已有文献[11, 12, 13]对此做过详细介绍,在此不赘述。其中,徐世浙院士[7, 8]对重磁位场向下延拓这一课题进行了系统的研究,提出了全新的位场向下延拓方法。其主要步骤是:将水平观测面上的位场实测值垂直投影至下部的延拓水平面上,作为该水平面上的位场初值;再根据该水平面上的初值,通过向上延拓计算观测面上的位场值;最后用观测面上的实测值与计算值的差值对延拓面上的位场值进行校正。如此反复迭代,直至观测面上的实测值与计算值的差值小到可以忽略。针对大数据量的网格数据,可将向下延拓深度提高到10~20倍点距。此后,不断有人对该方法进行补充完善,主要进展有:
刘东甲等[11]把迭代下延法的空间域迭代过程变换到波数域(频率域),得到了位场向下延拓的波数域迭代法,并从波数域迭代公式出发证明了其收敛性,即当迭代次数n趋于无穷时,第n次迭代的位场波谱趋于向下延拓场的波谱。
骆遥[12]提出了一个下延异常逐次分离的过程,阐述了该过程即为迭代法下延的物理实质。通过对可下延异常逐次进行分离,将位场分离成可下延的区域场(信息)和剩余异常(噪声)两部分,并对分离出的区域场进行向下延拓,其累计向下延拓结果的频谱逼近于频率域下延谱。剩余异常的频谱经不断分离而被压制,说明迭代过程本身是不断收敛的。研究者认为如何减少剩余异常的噪声水平是迭代法下延中有待深入探讨和解决的问题。
姚长利等[13]认为迭代法是近来在研究中受到普遍重视的方法技术,虽然也取得了较好的成果,但也存在对迭代法研究还不够深入、对其存在的缺点认识不够充分和客观等问题。其推导了迭代法的通式,并分析了对迭代法收敛性影响的各种因素后指出:映射函数决定着迭代法是否收敛;增加迭代次数虽然能够使计算收敛到FFT直接计算理论结果,但如果该理论结果本身就是不稳定的,则迭代法计算如果收敛,也是收敛到一个不稳定的结果。所以针对位场处理转换中一些不稳定计算采用迭代法,并没有从根本上解决计算的不稳定性问题。研究者[13]突出了“向下延拓迭代法主要过程是向上延拓而不是向下延拓”这一概念,笔者认为这一概念代表了问题的本质。
通过研究我们认为,为了深刻理解方法的本质,应该对“向上延拓而不是向下延拓”做详细的剖析,同时还应该突出“迭代的结果趋近于观测值”这一实际操作过程,并证明其收敛性。因此,研究迭代数据在空间域的变化规律以及迭代数据与观测值之间的关系,就成了必要的事情。为了简便起见,并不失一般性,在本文中,笔者以剖面磁异常向下延拓为例,按照向下延拓迭代法的步骤,通过追踪迭代过程中数据的变化(研究迭代过程与观测值之间的动态关系),得到了迭代数据在空间域的变化规律;并从不同途径证明空间域迭代法的收敛性,用模型试验结果说明迭代的位场初值可以任意给定;最后,对实际操作中可能出现的、不能达到误差标准的情况进行了探讨。
以上工作将使得位场向下延拓迭代法理论更加完善。
1 迭代法位场向下延拓原理简述迭代法位场向下延拓原理和步骤[7]简述如下。
ΓA与ΓB之间是无源空间(图 1)。用u(x,0)代表高度ΓA(z=0)的位。用
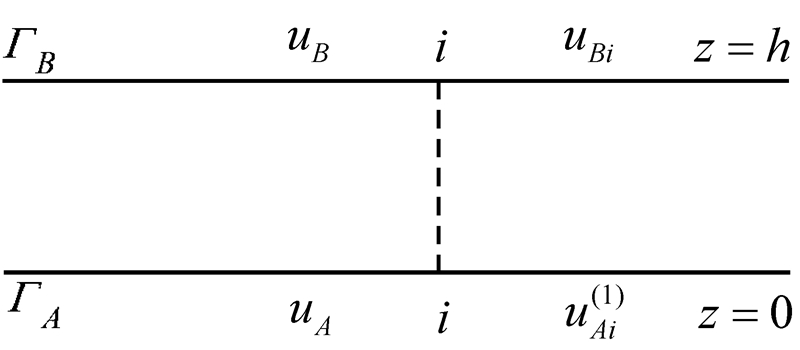 |
| 图 1 观测高度ΓB 与延拓高度ΓA的位置 Fig. 1 Location of observation height ΓB and continuation height ΓA |
| |
表示u(x,0)的傅里叶变换。其中,k是波数。则高度ΓB (z=h)上的位是
其中,F-1是傅里叶反变换。式(2)是频率域的延拓公式。当h>0 时,为向上延拓,延拓很稳定;当h<0时,为向下延拓,延拓很不稳定。
设ΓB高度的位uB是已知的,其下ΓA高度的位uA是待求的,ΓA,ΓB之间没有场源。迭代法向下延拓的步骤如下:
1)将ΓB上的位uB垂直放置在ΓA的对应点上,作为uA的初值。
2)从uA的初值,用公式(2)计算ΓB上的位,也可以用其他空间域的方法计算。
3)根据ΓB上原始值与计算值的差值,对ΓA上的uA进行校正。
4)如此反复迭代,直至观测高度上的实测值与计算值的差值小到可以忽略。一般迭代20~50次即可。
这种方法的位场向下延拓比简单的FFT稳定得多,可以向下延拓较大的距离。
2 向下延拓迭代法的数据流分析及收敛性 2.1 迭代法向下延拓的具体操作过程为了分析向下延拓迭代法的收敛性,先分析其具体操作过程。
将ΓB上的位uB(或写作uB0)作为uA的初值,用公式(2)计算ΓB上的位。于是迭代法向下延拓在空间域的具体执行 (数据追踪) 情况如表 1所示。表 1中各符号的意义如图 2所示。
| 迭代次数 | uA的初值 | 上延结果 | 差 |
| 0 | uB | uB1 | uB1-uB |
| 1 | 2uB-uB1 | 2uB1-uB2 | 2uB1-uB2-uB |
| 2 | 2uB-2uB1+uB2 | 2uB1-2uB2+uB3 | 2uB1-2uB2+uB3-uB |
| 3 | 2uB-2uB1+2uB2-uB3 | 2uB1-2uB2+2uB3-uB4 | 2uB1-2uB2+2uB3-uB4-uB |
| | | | |
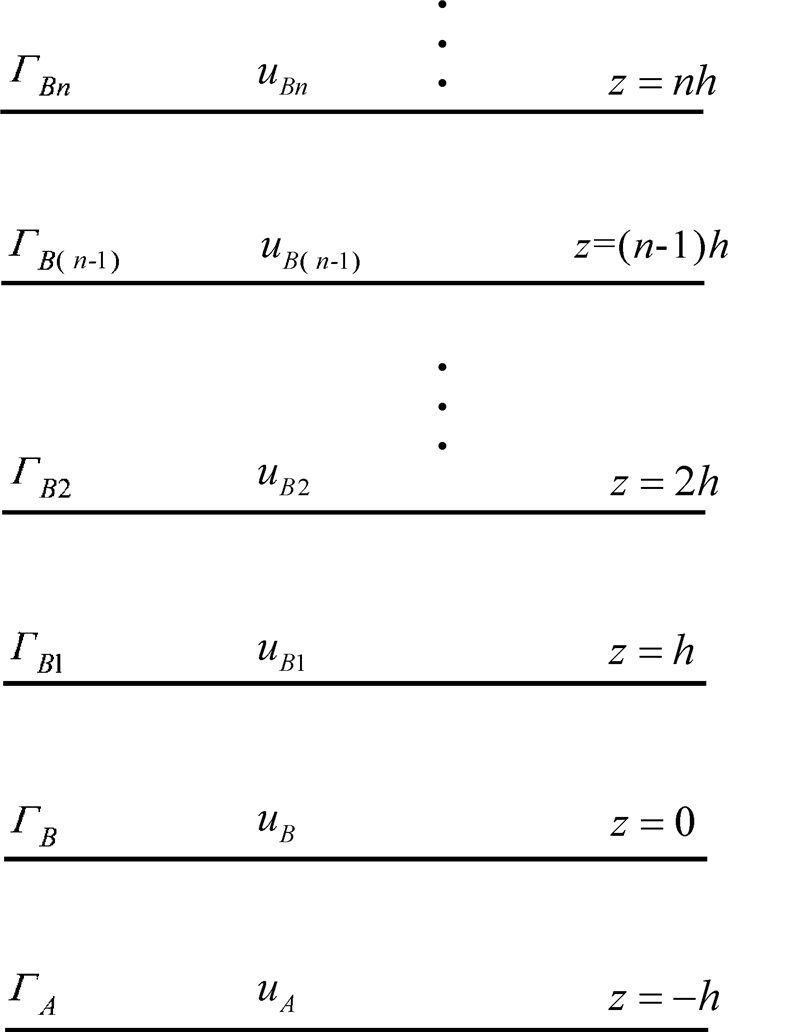 |
| 图 2 迭代过程中涉及的各个高度 Fig. 2 Altitude involved in iteration |
| |
一般地,设uA的初值为P,上延结果为Q,原始值与计算值的差为D,用原始值与计算值的差对计算值进行校正后的值为C,则对于每一次迭代有
式中,n为迭代次数。
从上面的分析可知: 1)用迭代法将观测高度的位场向下延拓一个深度h,实际上是通过不同高度的向上延拓来实现的,迭代次数增加一次,涉及的上延平面就增大一个h高度的平面。一般地,迭代次数n与上延高度h的关系为n~(n+1)h。 2)如果观测高度上的实测值与计算值的差值小到可以忽略,则将本次迭代使用的初值作为向下延拓的结果(根据向下延拓的步骤 4))。
2.2 向下延拓迭代法的收敛性根据公式(1)和公式(2),有
式中:h≥0;i=0,1,2,…,n。式(7)说明,在频率域,随着i递增,U(k,ih)递减。而由表 1可见,在空间域中,初值、上延结果、差以及每一次校正后的结果都能以一个交错级数表示,而且结合傅里叶变换的性质和根据场论分析满足下列条件:1) uBi≥uBi+1 ;2) limi→∞uBi=0 ;i=1,2,…,n。根据莱布尼兹定理,表 1中每一次上延结果都是收敛的,且其和Q≤uB。
也可以从另一方面论述迭代法的收敛性。因为迭代法是以“观测高度上的实测值与计算值的差值小到可以忽略”为标准,从表 1(或式(4))我们期望有
两边做傅里叶变换得
即期望有
而式(9)中公比为e-kh的交错级数的无穷等比数列的和为
其中,k的取值范围为〔0,∞〕。故也能推出上延结果的和Q≤uB的结论。
因此,当迭代次数趋近于无穷时,原始值与计算值的差为
可以推论,对于有限的任意初值,每一次的上延结果是收敛的,且其和Q≤uB。
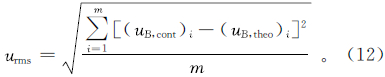
3 关于向下延拓迭代法的误差标准和初值给定根据迭代法步骤 4),向下延拓迭代法的均方误差可以写成(用于模型试验,主要与模型和计算精度有关)
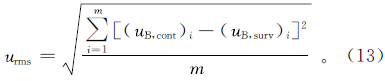
式中: uB,cont和uB,theo分别是ΓB高度上的位场延拓值和理论值;m是计算所用的点数。或者,均方误差也可以写成(用于实测值,主要与实测值精度以及异常的复杂程度有关)
式中: uB,surv是ΓB高度上的位场实测值。
对于式(12),根据需要也可以在绝对误差
的约束下用模型试验来检验迭代法的收敛速度、结果的可信程度(例如最大值之比)等。显然,式(14)较式(12)要严格得多。
图 3即是一个板状磁性体模型利用不同的误差标准得到的算例。板体的倾角为60°,磁化倾角为45°。板体半宽度为20 m,上顶埋深为200 m,点距为10 m,剖面长度为1 280 m。把磁性体上方200 m高度的磁异常向下延拓到磁性体上方50 m高度。试验中所用的不同误差标准和误差公式对应的迭代次数、计算异常最大值与理论异常最大值之百分比列于表 2,迭代初值为观测高度上的理论异常值(也试验了迭代初值为常数或0值的情况,结果相同)。从表 2看出,给定的误差标准越严格,向下延拓结果与理论曲线越逼近,但迭代次数增多。
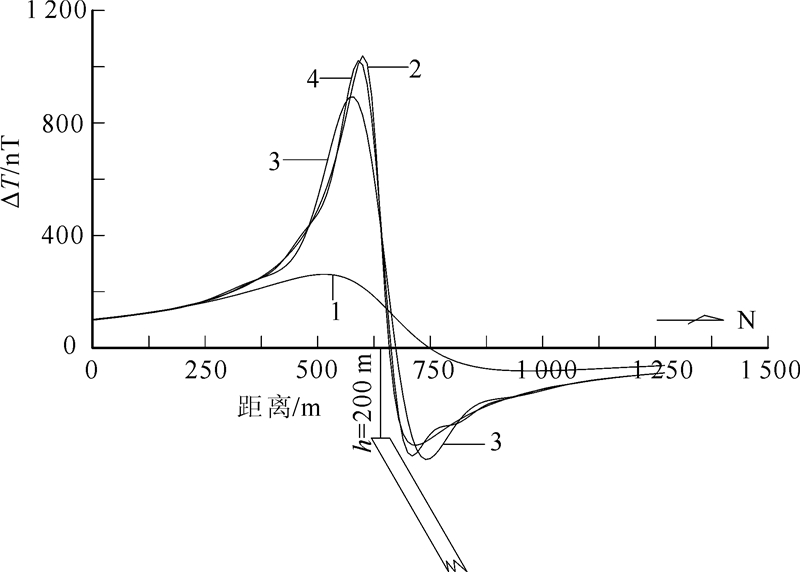 |
| 1.理论磁异常(h=200 m);2.理论磁异常(h=50 m);3.向下延拓磁异常(h=50 m,ε=1.0 nT);4.向下延拓磁异常(h=50 m,ε=0.01 nT)。 图 3 板体模型磁异常向下延拓算例 Fig. 3 Example of magnetic anomaly downward continuation by a dike model |
| |
| urms/ nT | 按照式(12) | 按照式(14) | ||
| n | E/% | n | E/% | |
| 1.0 | 40 | 80 | 89 | 85 |
| 0.1 | 224 | 91 | 503 | 94 |
| 0.01 | 1 262 | 97 | 2 866 | 98 |
| 注:E为计算异常最大值与理论异常最大值之百分比。 | ||||
图 4a为一个球状磁性体模型按照式(12)给定的误差标准为0.1 nT、迭代初值数据组为0得到的算例。球体半径为100 m,中心深度为500 m,磁化倾角为50°,磁化偏角为0°,线距和点距均为50 m,计算了边长为5 000 m 的方形面积的磁异常。图 4b为从平面图中心部位截取的剖面示意图(图中纵横距离单位未按比例)。把磁性体中心上方500 m高度平面的磁异常向下延拓到磁性体上方300 m高度的平面(即下延200 m)。图 4a中计算值与理论异常值符合得相当好,因此曲线没有用不同线条来表示。图a边部的0值等值线,是计算产生的噪声。
 |
|
a.平面等值线图 ; b.剖面示意图。 1.理论磁异常(h=500 m);2.理论磁异常(h=300 m);3.向下延拓磁异常(h=300 m,Urms=0.1 nT)。 图 4 球体模型磁异常向下延拓算例 Fig. 4 Example of magnetic anomaly downward continuation by a spherical model |
| |
对于该球状磁性体模型,利用不同的初值以及按照式(12)给定不同的误差标准进行试验,试验结果列于表 3。表 3也说明,给定的误差标准越严格,向下延拓结果与理论曲线越逼近,但迭代次数增多。板状体二维模型和球体三维模型算例还说明,迭代初值不一定必须用地面观测值uB,可使用任意有限数据,包括常数(包括0值),即从不同的初值出发,把磁性体上方的磁异常向下延拓到磁性体上方某个高度,都能得到收敛的结果:迭代法不受初值的model影响。这与第3节的数学推论是一致的。在用式(12)、式(13)或者式(14)给定误差标准时,要考虑既不会因过于严格而造成迭代误差标准得不到满足,又不会因过于宽松而“欠迭代”从而造成向下延拓“不到位”的结果。显然,在迭代法实际应用中,误差标准、实测值精度以及异常的复杂程度,都是影响迭代次数和向下延拓结果的重要因素。对于式(13),定性地讲:受偶然误差影响的实测值可以用较小的误差标准,受系统误差影响的实测值就要用较大的误差标准;对于简单异常可以用较小的误差标准,对于复杂异常就要用较大的误差标准。
| urms/ nT | 迭代初值: 理论异常值 | 迭代初值: 100 nT | 迭代初值: -400 nT | 迭代初值: 0 nT | ||||
| n | E/% | n | E/% | n | E/% | n | E/% | |
| 10 | 3 | 45 | 3 | 45 | 3 | 45 | 3 | 45 |
| 5 | 5 | 59 | 5 | 59 | 5 | 59 | 5 | 59 |
| 1 | 13 | 80 | 13 | 80 | 13 | 80 | 13 | 80 |
| 0.1 | 47 | 94 | 47 | 94 | 47 | 94 | 47 | 94 |
| 0.04 | 92 | 97 | 93 | 97 | 93 | 97 | 92 | 97 |
1)迭代法向下延拓是通过不同高度的向上延拓来实现的,随着迭代次数的增加,涉及的上延高度增大。一般地,迭代次数n与上延高度h的关系为n~(n+1)h。
2)迭代过程形成一系列交错级数,每一次上延结果都是收敛的,且其和Q≤uB。模型试验说明,随着迭代次数的增加,迭代结果收敛于观测高度上的实测值。
3)数学推论和模型试验还说明迭代初值可使用任意有限数据,迭代法的收敛性与初值无关。
4)误差标准关联着迭代次数。误差标准越严格,下延结果会更“到位”,而迭加次数也会增加。值得注意的是,实际中存在着达不到误差标准的情况。
5)在迭代法实际应用中,误差标准、实测值精度以及异常的复杂程度,都是影响迭代次数和向下延拓结果的重要因素,这在实际应用中需引起注意,也值得今后进一步研究。
| [1] | Fedi M,Florio G.A Stable Downward Continuation by Using the ISVD Method[J].Geophysical Journal International,2002,151(1):146-156. |
| [2] | Cooper G.The Stable Downward Continuation of Potential Field Data[J].Exploration Geophysics,2004,35(2):260-265. |
| [3] | 刘保华,焦湘恒,王重德.位场向下延拓的边界单元法[J].石油地球物理勘探,1990,25(4):495-499. Liu Baohua,Jiao Xiangheng,Wang Chongde.Boundary Element Method for Continuation of Potential Field[J]. Oil Geophysical Prospecting, 1990,25(4):495-499. |
| [4] | 毛小平,吴蓉元,曲赞.频率域位场下延的振荡机制及消除方法[J].石油地球物理勘探,1998,33(2):230-237. Mao Xiaoping,Wu Rongyuan,Qu Zan. Oscillation Mechanism of Potential Field Downward Continuation in Frequency Domain and Its Elimination[J]. Oil Geophysical Prospecting, 1998,33(2):230-237. |
| [5] | 徐世浙,沈晓华,邹乐君,等.将航磁异常从飞行高度向下延拓至地形线[J].地球物理学报,2004,47(6):1127-1130. Xu Shizhe,Shen Xiaohua,Zou Lejun,et al.Downward Continuation of Aeromagnetic Anomaly from Flying Altitude to Terrain[J].Chinese Journal of Geophysics,2004,47(6):1127-1130. |
| [6] | 徐世浙.位场延拓的积分-迭代法[J].地球物理学报,2006,49(4):1176-1182. Xu Shizhe.The Integral-Iteration Method for Continuation of Potential Fields[J].Chinese Journal of Geophysics,2006,49(4):1176-1182. |
| [7] | 徐世浙.迭代法与FFT法位场向下延拓效果的比较[J].地球物理学报,2007,50(1):285-289. Xu Shizhe.A Comparison of Effects Between the Iteration Method and FFT for Downward Continuation of Potential Fields[J].Chinese Journal of Geophysics,2007,50(1):285-289. |
| [8] | 徐世浙,余海龙.位场曲化平的插值-迭代法[J].地球物理学报,2007,50(6):1811-1815. Xu Shizhe, Yu Hailong.The Interpolation-Iteration Method for Potential Field Continuation from Undulating Surface to Plane[J].Chinese Journal of Geophysics,2007,50(6):1811-1815. |
| [9] | 王彦国,王祝文,张凤旭,等. 位场向下延拓的导数迭代法[J].吉林大学学报:地球科学版,2012,42(1): 240-245. Wang Yanguo,Wang Zhuwen,Zhang Fengxu,et al. Derivative-Iteration Method for Downward Continuation of Potential Fields[J]. Journal of Jilin University:Earth Science Edition, 2012,42(1): 240-245. |
| [10] | 张志厚,吴乐园. 位场向下延拓的相关系数法法[J].吉林大学学报:地球科学版,2012,42(6): 1912-1919. Zhang Zhihou,Wu Leyuan. Corelation Coefficient Method for Downward Continuation of Potential Fields[J]. Journal of Jilin University:Earth Science Edition, 2012,42(6): 1912-1919. |
| [11] | 刘东甲,洪天求,贾志海,等.位场向下延拓的波数域迭代法及其收敛性[J].地球物理学报,2009,52(6):1599-1605. Liu Dongjia,Hong Tianqiu,Jia Zhihai,et al.Wave Number Domain Iteration Method for Downward Continuation of Potential Fields and Its Convergence[J].Chinese Journal of Geophysics,2009,52(6):1599-1605. |
| [12] | 骆遥.位场迭代法向下延拓的地球物理含义:以可下延异常逐次分离过程为例[J].地球物理学进展,2011,26(4):1197-1200. Luo Yao.The Integral-Iteration Method for Continuation of Potential Fields: A Case by Computing Regional Anomaly Can be Continued Downward[J].Progress in Geophysics,2011,26(4):1197-1200. |
| [13] | 姚长利,李宏伟,郑元满,等.重磁位场转换计算中迭代法的综合分析与研究[J].地球物理学报,2012,55(6):2062-2078. Yao Changli, Li Hongwei, Zheng Yuanman, et al. Research on Iteration Method Using in Potential Field Transformations[J]. Chinese Journal of Geophysics,2012,55(6):2062-2078. |