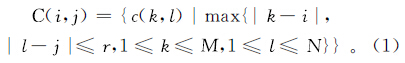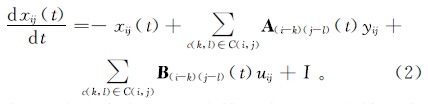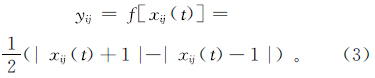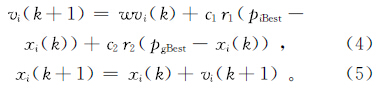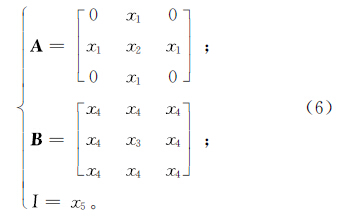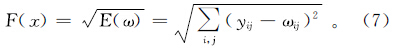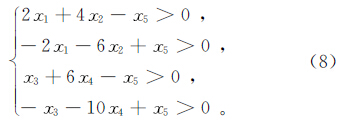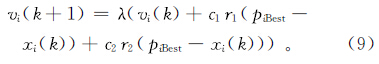2. 青岛海洋地质研究所国土资源部海洋油气资源与环境地质重点实验室, 山东 青岛 266071
2. The Key Laboratory of Marine Hydrocarbon Resources and Environment Geology, Qingdao Institute of Marine Geology, Qingdao 266071, Shandong, China
0 引言
油气储层往往比围岩密度小,会在其上方产生重力低异常值,但油气产生的重力异常普遍很微弱,而且被背景构造产生的重力异常掩盖,难以识别。国内外学者利用不同方法从不同角度进行了油气重力异常的提取研究,如归一化总梯度方法[1]、插值切割法[2]、小波提取法[3, 4]等,可是这些方法对于微弱的油气异常提取效果并不好。
细胞神经网络(cellular neural network,CNN)是L. O. Chua在1988年提出的[5]。Muhittin等[6, 7]首次将CNN用于重力异常的分离,说明该方法能够突出浅层异常、压制区域异常。刘展等[8]使用拟BP算法改进了CNN方法,对花沟地区火成岩重力异常进行提取,并且总结了CNN方法的适用条件。但以上方法存在参数设置比较复杂,容易陷入局部极小解等缺点。针对以上不足,笔者将粒子群算法应用到CNN模板设计中。粒子群优化(particle swarm optimization,PSO)算法是由Jim Kennedy 于1995年提出的随机全局优化方法[9],同其他算法相比较,其优势为没有过多参数需要调整,能比较快速地找到最优解[10, 11, 12, 13, 14, 15]。在本文中,笔者结合CNN动态性能分析,使用粒子群算法优化设计CNN的模板参数,并对油气重力异常信息进行提取,用粒子群算法对CNN模板参数优化并进行油气重力异常信息提取,通过对比分析说明得到参数的合理性和有效性。 1 细胞神经网络原理
细胞神经网络中的一个细胞仅与它的近邻细胞相连接,近邻细胞可以彼此直接相互作用,因为神经网络连续时间动力学的传播效应,非近邻细胞不直接连接[16]。细胞神经网络中细胞的邻域C(i,j)定义为
式中:r为半径;M,N分别为横坐标和纵坐标方向的搜索最大值。则状态方程为 其中:xij为状态变量;yij为输出变量;uij为输入变量;I为偏量;A为反馈系数矩阵;B为控制吸收系数矩阵;t为模型参数。输出方程为 其中,f(x)为分段线性函数,通过对A、B、I的设计优化实现油气重力异常信息提取。 2 粒子群算法原理PSO中,每个优化问题的解都是搜索空间的一个“粒子”的状态,所有粒子都由一个适应函数(fitness function)决定适应值(fitness value),每个粒子还有一个速度直接影响它们的飞翔方向和距离,粒子根据当前自身情况和粒子群情况在解空间中搜索[17]。假设在D维搜索空间中,有m个粒子,其中第i个粒子的位置和速度分别是xi=(xi1,xi2,…,xiD),vi=(vi1,vi2,…,viD),i=1,2,…,m,将vi带入目标函数可计算其适应值。记第i个粒子搜索到的最优位置为piBest=(pi1,pi2,…,piD),整个粒子群搜索到的最优位置为pgBest=(pg1,pg2,…,pgD),则根据公式(4)和(5)可更新粒子的速度和位置:
其中:ω是非负常数,称为惯性因子,w也可以随着迭代线性地减少;学习因子c1和c2是非负常数;r1和r2是[0, 1]之间的随机数;vi∈[vmin,vmax],vmin和vmax由人为设定。迭代中止条件为最大迭代次数或粒子群迄今为止搜索到的最优位置满足阈值。 3 基于粒子群算法的细胞神经网络模板学习方法 3.1 种群参数的确定由于细胞神经网络具有空间不变性,因此进行油气重力异常信息提取时,采用如下模板格式:
由模板可知,需要用PSO算法对x1,x2,x3,x4,x5五个参数进行优化。 3.2 适应度函数将细胞神经网络输出端误差E(ω)的平方根作为PSO算法的适应度函数[18, 19, 20]:
式中:y3是指神经网络的输出;ωij是期望输出。 3.3 带约束条件的粒子群算法(C-PSO)优化CNN模板参数通过对CNN的动态性能分析[21, 22, 23, 24],得到用于油气重力异常信息提取的五个模板参数有如下关系:
将式(8)作为一种约束对CNN模板进行优化,可以使种群较快地收敛到最优值。此外,为了提高收敛速度,对式(4)引入收缩因子λ:
其中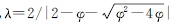 ,,φ=c1+c2,且φ > 4。
3.4 C-PSO算法的实现
,,φ=c1+c2,且φ > 4。
3.4 C-PSO算法的实现
基于粒子群优化细胞神经网络模板的流程图如图1所示。
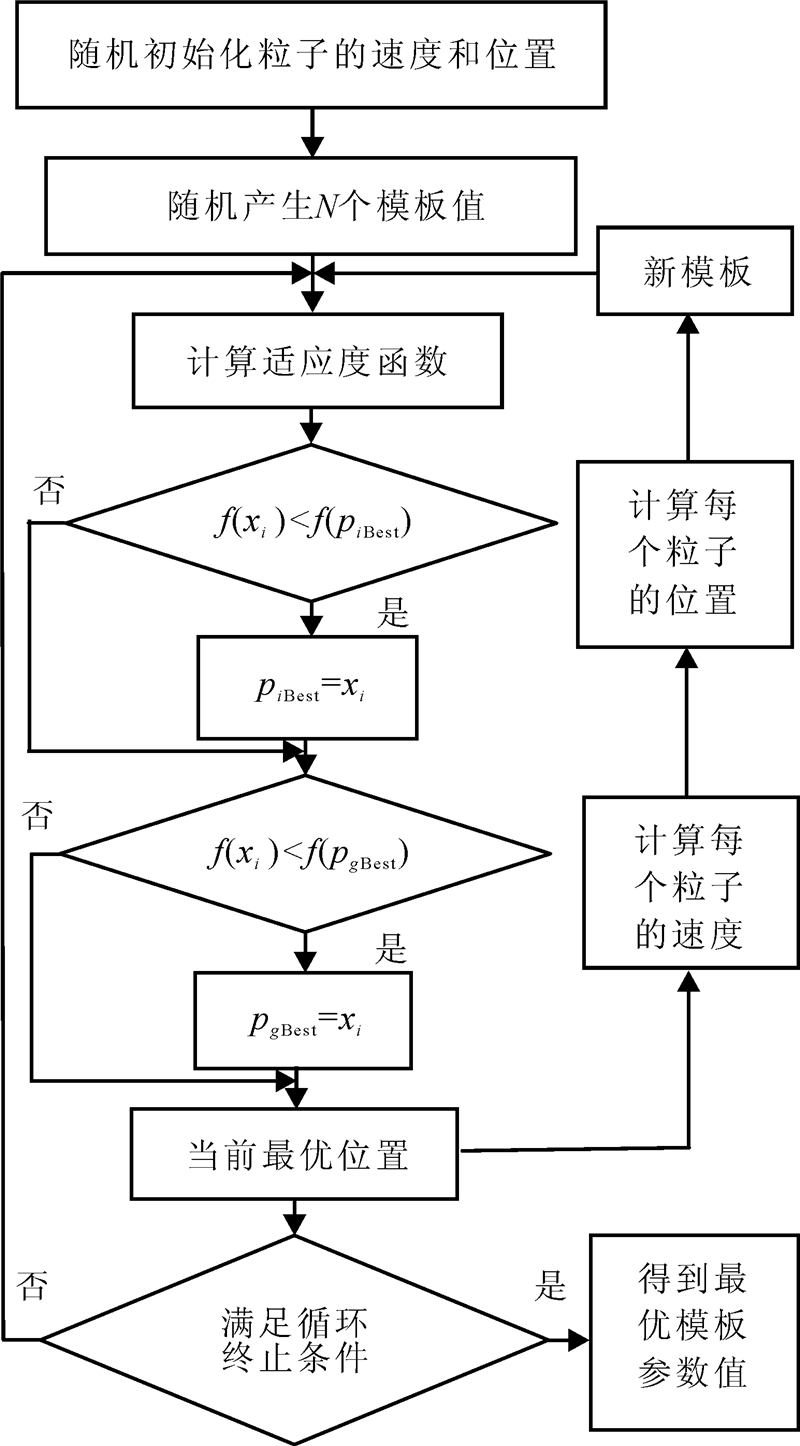 |
| 图 1 基于粒子群优化细胞神经网络模板的流程图Fig. 1 Flow chart of templates of CNN based on PSO |
为了验证方法的有效性,首先建立三球体模型:用一个放置在深部的球体(球1)模拟区域异常,在浅层放置两个较小的球体(球2、球3)模拟局部异常,参数如表1所示。此三球体模型的叠加重力异常如图2a所示,图2b为两个浅层球体(球2、球3)的叠加重力异常。将浅部小球球2和球3的叠加重力异常作为细胞神经网络的期望输出,使用拟BP、PSO、C-PSO三种算法分别对模板参数进行优化。表2为三种算法得到的提取重力异常信息的模板,表3为三种算法的迭代次数和时间。从表3可以看出,C-PSO算法寻找最优值的迭代次数和迭代时间都明显小于拟BP和PSO算法。
| 球体 | 球心坐标/km | 球心埋深/m | 半径/m | 密度/ (g/cm3) |
| 球1 | (80,80) | 2 000 | 1 000 | 0.10 |
| 球2 | (40,80) | 1 800 | 700 | 0.08 |
| 球3 | (40,40) | 1 500 | 400 | 0.06 |
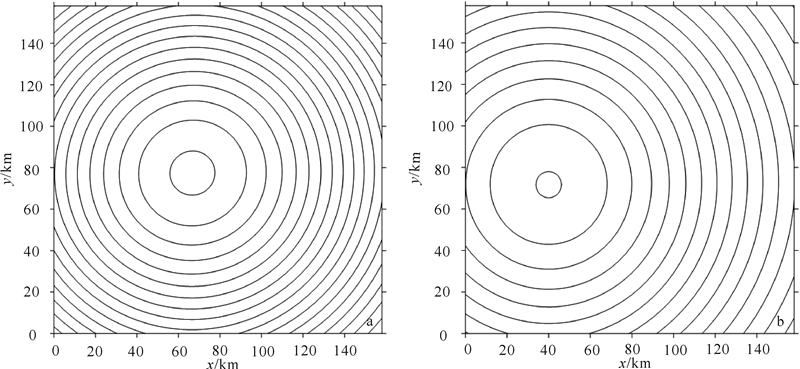 |
| 图 2 三个(a)和两个(b)浅层球体重力叠加异常Fig. 2 Gravity anomaly of three spheres (a) and two shallow spheres (b) |
| 拟BP算法 |  |
| PSO算法 |  |
| C-PSO算法 | 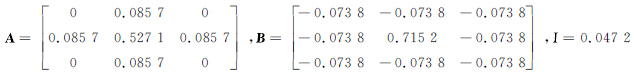 |
| 迭代次数 | 迭代时间/s | |
| 拟BP算法 | 73 | 33 |
| PSO算法 | 32 | 11 |
| C-PSO算法 | 17 | 7 |
建立四球体模型,参数如表4所示。使用表1中的三个模板对模型进行重力异常信息提取,结果如图3所示。从图3可以看出:C-PSO算法优化模板提取的重力异常信息明显要比拟BP算法的准确,抗噪性更好;而与PSO算法对比,两者得到的结果几乎一致。但由4.1节知C-PSO算法要比PSO算法快。综上所述,C-PSO算法在优化提取重力异常信息CNN模板时要优于其他两种算法。
| 球体 | 球心坐标/km | 球心埋深/m | 半径/m | 密度/(g/cm3) |
| 球1 | (80,80) | 2 000 | 1 000 | 0.10 |
| 球2 | (91,93) | 1 800 | 700 | 0.08 |
| 球3 | (68,94) | 1 500 | 400 | 0.06 |
| 球4 | (69,66) | 1 500 | 600 | 0.09 |
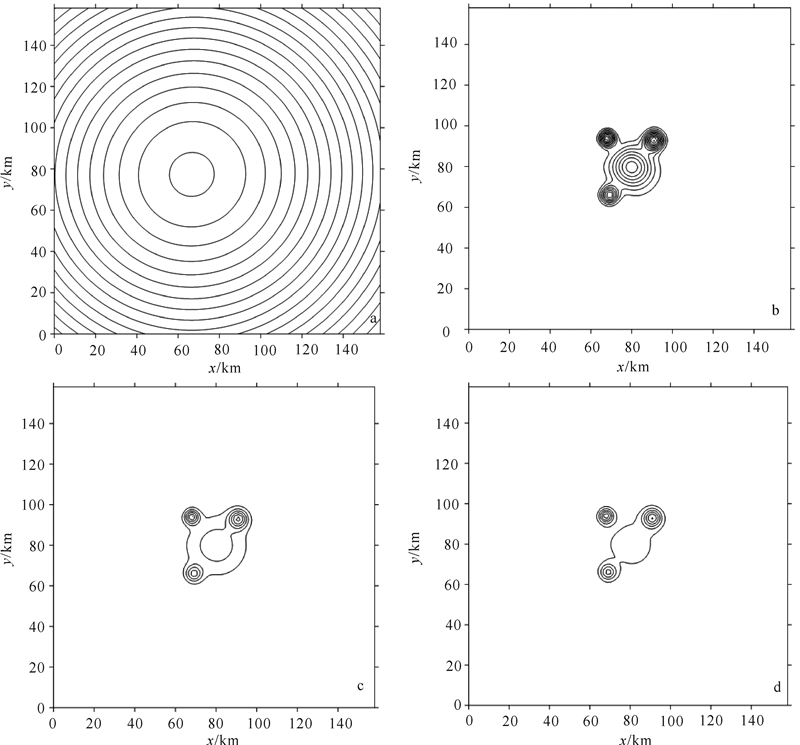 |
| a. 四球模型叠加重力异常;b. 拟BP算法处理结果;c. PSO算法处理结果;d. C-PSO算法处理结果。 图 3 四球体模型原始重力异常及三种方法提取的异常Fig. 3 Original gravity anomaly of four spheres and the anomaly extracted by three methods |
建立背斜油气藏模型,纵向和横向长度均为100 km,油气储层位于第三层,剩余密度为-0.10 g/cm3,从上向下各层剩余密度依次为0.50、0.75、1.00、1.50 g/cm3。图4为在y=50 km处、平行于横轴的模型横切面图。
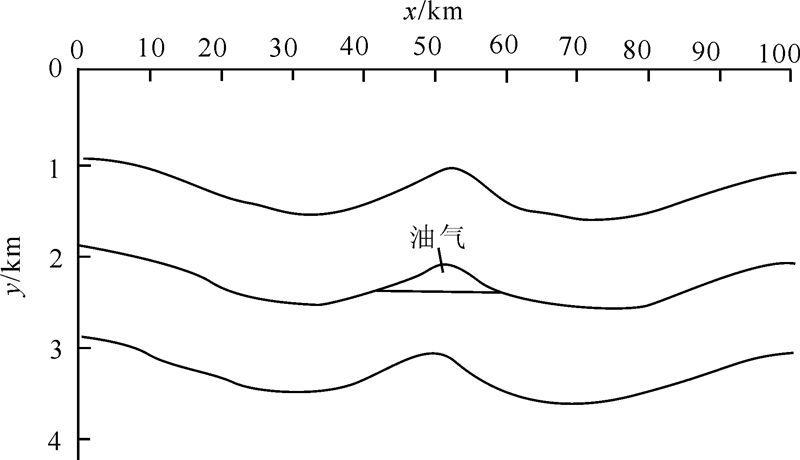 |
| 图 4 油气藏模型横切面图Fig. 4 Cross-sectional diagram of reservoir model |
图5a为油气藏模型产生的重力异常。由于区域异常的掩盖,在图5a中看不出油气异常信息。使用表2中C-PSO算法得到的模板进行油气异常信息提取,结果如图5b所示。从图5b中可以看出,背斜构造引起的区域异常被消除,提取的相对重力负异常对应储层位置。说明该方法能够提取油气异常信息,消除区域异常干扰。
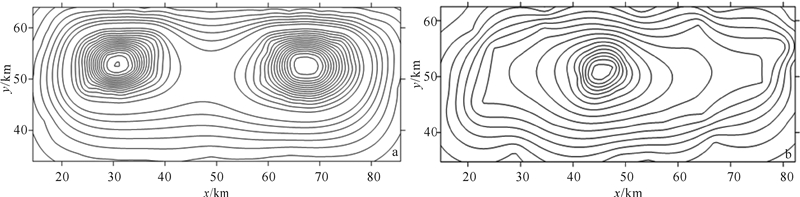 |
| 图 5 原始重力异常(a)及C-PSO算法提取的异常(b)Fig. 5 Original gravity anomaly (a) and the anomaly extracted C-PSO algorithm (b) |
笔者利用C-PSO算法优化的CNN模板对柴达木盆地三湖地区涩北实测重力资料进行油气重力异常信息提取。该地区天然气主要产自第四系湖相沉积地层,气田区地层密度比周围同一套地层密度低0.10 g/cm3左右,是典型的背斜油气藏。因此,使用本文4.3节中的模型进行模板训练,得到的模板为
图6a为涩北的实测重力异常,气田区地层密度比周围地层密度低,因此在其上方产生相对重力低;但由于构造等因素的影响,并不能确定气田范围。使用模板(10)对涩北勘探区进行油气重力异常信息提取,结果如图6b所示。从图6b中可以看出提取的油气重力异常信息与已知的工业气井有很好的对应关系;说明该方法能够压制区域异常,提取油气异常信息,圈定油气边界,并且有较强的抗干扰能力。
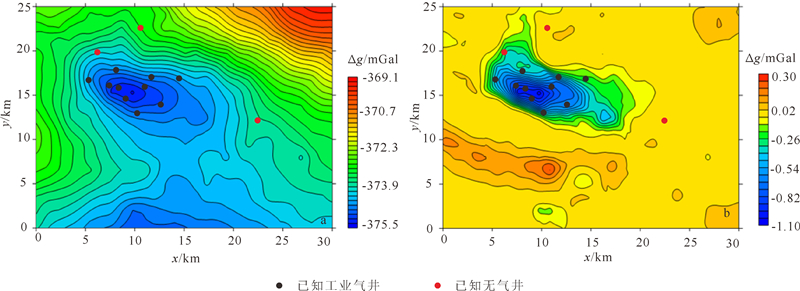 |
| Δg为重力异常。 图 6 涩北原始重力异常(a)及C-PSO算法处理结果(b)Fig. 6 Gravity anomaly of Sebei (a) and reservoir gravity anomaly extracted by C-PSO (b) |
本文提出的C-PSO算法优化细胞神经网络模板在提取重力异常信息时,无论是在迭代步数、时间、搜索精度上均优于拟BP和PSO算法,该算法能够根据自己的期望训练模板,更精准地提取油气重力异常信息,消除或减弱其他干扰。
需要指出的是,在提取油气重力异常信息时,该方法需要大量初始模型训练模板,因此要足够多的先验信息才能够保证结果的准确性。后续工作中,我们将重点研究如何在保证精度的前提下,减小方法对先验信息的依赖。
| [1] | 张凤旭,孟令顺,张凤琴,等.利用Hilbert变换计算重力归一化总梯度[J].地球物理学报,2005,48(3):704-709. Zhang Fengxu, Meng Lingshun, Zhang Fengqin, et al. Calculating Normalized Full Gradient of Gravity Anomaly Using Hilbert Ttransform[J]. Chinese Journal of Geophysics, 2005,48(3):704-709. |
| [2] | 张刚. 油气重磁异常识别及提取方法研究[D].青岛: 中国石油大学, 2011. Zhang Gang. The Method Rresearch of Identification and Extraction of Oil Gravity and Magnetic Anomalies[D]. Qingdao: China University of Petroleum, 2011. |
| [3] | 耿喜哲,张春华. 综合小波分析与分形方法进行弱磁异常识别[J].物探与化探, 2002, 26(2): 126-130. Geng Xizhe, Zhang Chunhua. The Application of Wavelet Analysis and Fractal Technique to the Recoganion of Micro-Magnetic Anomaly[J]. Geophysical & Geochemical Exploration, 2002, 26(2): 126-130. |
| [4] | 宋双, 刘天佑, 苏俊青. 重磁小波多尺度分解及在火山岩识别中的应用[J]. 工程地球物理学报, 2008, 5(6): 675-679. Song Shuang, Liu Tianyou, Su Junqing. The Wavelet Multi-Scale Decomposition of Gravity and Magnet and Its Application in the Identification of Volcanic Rock[J]. Chinese Journal of Engineering Geophysics, 2008, 5(6): 675-679. |
| [5] | Chua L O, Yang L. Cellular Neural Networks:Theory[J]. IEEE Trans on Circuits, 1988,35(5): 1273-1290. |
| [6] | Albora A M,Ucan O N,Ozmen A,et al. Septaration of Bouguer Anomaly Map Using Cellular Neural Network[J]. Journal Applied Geophysics, 2001, 46:129-142. |
| [7] | Albora A M,Ozmen A. Wavelet Based Design of Dynamical Neural Networks for Magnetic Map Processing[R].Istanbul:University of Istanbul Press,2002:133-140. |
| [8] | 刘展,刘茂成,魏巍,等.重力异常分离的细胞神经网络方法研究[J].中国石油大学学报:自然科学版,2010,31(1):31-34. Liu Zhan, Liu Maocheng, Wei Wei, et al. A Gravity Anomaly Separation Method Based on Cellular Neural Network[J]. Journal of China University of Petroleum: Edition of Natural Science, 2010, 31(1): 31-34. |
| [9] | Kennddy J, Eberhart R. Particle Swarm Optimization[C]// Proceedings of IEEE International Conference on Neutral Networks. Perth: IEEE, 1995:1942-1948. |
| [10] | Eberhart R C, Shi Y. Particle Swarm Optimization: Developments, Applicationgs and Resources[C]// Pro Congress on Evolutonary Computation 2001. Piscataway: IEEE, 2001: 81-86. |
| [11] | 卢珊萍,于盛林.基于粒子群算法的细胞神经网络模板参数设计[J].计算机技术与发展,2009,19(4):83-86. Lu Shanping, Yu Shenglin. A Template Design Method for Cellular Neural Network Based Particle Swarm Optimizer Algorithm[J]. Computer Technology and Development, 2009,19(4):83-86.[HQ] |
| [12] | Karakuzu C. Parameter Tuning of Fuzzy Sliding Mode Controller Using Particle Swarm Optimization[J]. International Journal of Innovative Computing Information and Control, 2010, 6(10): 4755-4770. |
| [13] | 马国庆,黄大年,杜晓娟,等.Hartley变换在位场(重、磁)异常导数计算中的应用[J].吉林大学学报:地球科学版,2014,44(1):328-335. Ma Guoqing, Huang Danian, Du Xiaojuan, et al. Hartley Transform in the Application of the Derivatives Date[J]. Journal of Jilin University: Earth Science Edition, 2014, 44(1):328-335. |
| [14] | 管志宁,侯俊胜.重磁异常反演的拟BP神经网路方法及其应用[J].地球物理学报,1998,41(2):242-251. Guan Zhining, Hou Junsheng. Inversion of Gravity and Magnetic Anomalies Using Pseudo-BP Neural Network Method and Its Application[J]. Chinese Journal of Geophysics, 1998,41(2):242-251. |
| [15] | 曾琴琴,王永华,吴文贤.二维磁异常的粒子群快速成像方法及其应用[J].吉林大学学报:地球科学版,2013,43(2):616-622. Zeng Qinqin, Wang Yonghua, Wu Wenxian. Fast Imaging of 2D Magnetic Anomaly by Particle Swarm Optimization and Its Application[J]. Journal of Jilin University: Earth Science Edition, 2013, 43(2): 616-622. |
| [16] | Chua L, Thiran P. An Analytic Method for Designing Simple Cellular Neural Networks[J]. IEEE Trans on Circuits and Systems, 1991, 38(11):1332-1341. |
| [17] | 范正国,刘前坤,黄旭钊,等.自适应重磁对应分析[J].吉林大学学报:地球科学版,2012,42(6):1904-1919. Fan Zhengguo, Liu Qiankun, Huang Xuzhao, et al. Adaptive Correlative Analysis Between Aeromagnetic and Gravity Anomaly[J]. Journal of Jilin University: Earth Science Edition, 2012, 42(6): 1904-1919. |
| [18] | Zarandy A, Stoeffets A K, Roska T,et al. Implementation of Binary and Gray-Scale Mathematical Morphology on the CNN Universal Machine[J]. IEEE Trans on CAS, 1998,45(2): 163-168. |
| [19] | 侯遵泽,杨文采.中国重力异常的小波变换与多尺度分析[J].地球物理学报,1997,40(1):85-95. Hou Zunze, Yang Wencai. Wavelet Transform and Multi-Scale Analysis on Gravity Anomalies of China[J]. Chinese Journal of Sinica, 1997,40(1):85-95. |
| [20] | 杨文采,施志群,侯遵泽,等.离散小波变换与重力异常多重分解[J].地球物理学报, 2001,44(4):534-541. Yang Wencai, Shi Zhiqun, Hou Zunze, et al. Discrete Wavelet Transform for Multiple Decomposition of Gravity Anomalies[J]. Chinese Journal of Geophysics, 2001,44(4):534-541. |
| [21] | Hinze W J, Aiken C V,Brozena J M,et al. New Standard for Reducing Gravity Data: The North American Gravity Database[J]. Geophysics, 2005,70(4): 346-365. |
| [22] | Wu Jianshe, Jiao Licheng. Synchronization in Dynamic Networks with Nonsymmetrical Time-Delay Coupling Based on Linear Feedback Controllers[J]. Physica, 2008, 387(3): 2111-2119. |
| [23] | Zhong W S, Stefanovski J D,Dimirovski G M,et al. Decentralized Control and Synchronization of Time-Varying Complex Dynamical Network[J]. Physica, 2009, 142(7): 151-167. |
| [24] | Krink T, Vesterstrom J S, Riget J. Particle Swarm Optimization with Spatial Particle Extension[C]//Proceeding of International Conference on Evolutionary Computation.[S.l.].IEEE, 2002: 1474-1497. |