0 引言
我国西南岩溶地区分布面积广阔的连片裸露碳酸盐岩[1],裂隙-管道是其主要的储水空间和导水通道。该地区降雨充沛,水资源丰富,但可利用量少;可溶岩成土速率缓慢,容许土壤流失量低,水土流失危险程度高。开展西南岩溶地区裂隙-管道含水介质中地下水运动规律的研究,为水资源合理利用和管理提供理论支撑,对推动岩溶水运动规律研究有重要意义。
裂隙-管道介质具有高度非均质性和各向异性,水动力过程极其复杂,并且野外试验测量方法和观测数据有限,水文地质参数难以获取,严重阻碍着人们深入研究裂隙介质地下水流运动规律。在裂隙-管道介质水动力学的发展过程中,建立和发展了多种数学模型:等效连续介质模型、双重介质模型、离散裂隙网络模型和耦合模型等[2]。这些数学模型简单方便,但其是在理想条件下建立,适用范围受到严重限制。物理模型在一定程度上可以按照野外实际的水文地质条件任意改变。近年来,随着模具制造水平的提高,众多研究者开始强调物理模型的重要性,因此通过试验手段研究管道、裂隙等多重介质对地下水水流系统的影响和控制作用成为热点[3, 4, 5, 6]。目前的物理模型模拟试验主要集中在单个平行板裂隙、单管道、多组平行裂隙或交叉裂隙上。由于裂隙-管道介质本身的复杂性,对裂隙网络,尤其是裂隙-管道物理模型的研究较少。
笔者通过对贵州后寨地区的水文地质条件进行概化,建立了裂隙-管道介质物理模型。选取补给雨强和泉口直径作为变量因子设计了多组正交试验,分析了其对泉流量过程的影响规律;进而采用Visual Modflow建立数值模型对物理试验结果进行模拟,以期探究岩溶含水系统内部结构和开采井等因素对泉流量过程的影响。
1 研究方法 1.1 水文地质概念模型裂隙-管道介质泉流域的水文地质概念模型是参照贵州省后寨岩溶小流域的含水系统建立的,主要包括含水层性质、水流运动特征、边界条件及补给排泄条件等几个方面[7]。贵州省后寨岩溶小流域的水文地质概念模型可以概化为图 1。岩溶含水介质分为上部的非饱和带和下部的饱和带;流域内层面裂隙和垂直层面裂隙纵横交错,落水洞星罗棋布,地下水流运动复杂,层流和紊流流态转换频繁;泉流域的边界条件一般是流量边界;流域内主要接受大气降水的分散补给和地表径流对落水洞的集中补给,地下河出口是排泄总出口[8],地下水以泉的形式排出。
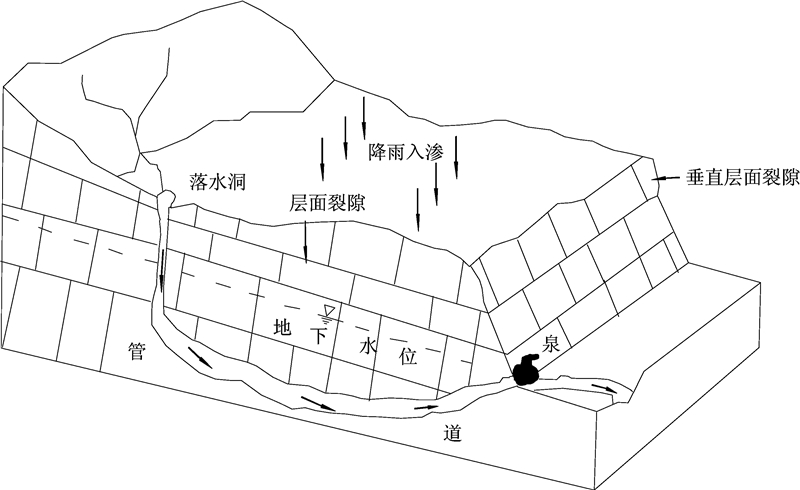 |
| 图 1 水文地质概念模型结构示意图 Fig. 1 Schematic diagram of the hydrogeological conceptual model |
| |
通过对裂隙-管道介质水文地质概念模型合理简化,建立如图 2所示的物理模型,主要包括三部分:降雨补给系统、裂隙-管道介质模拟区、水头采集系统。
 |
| a. 示意图;b. 实物图(①正视图;②后视图;③侧视图)。 图 2 裂隙-管道介质物理模型 Fig. 2 Physical analog of fissure-conduit media |
| |
降雨补给系统通过水箱补给模拟降雨过程,水箱顶部泄流口控制水箱内水头为定水头,雨强大小通过水箱阀门进行调节。裂隙-管道介质模拟区长1.29 m,高0.895 m,宽0.03 m,其材料为光滑有机玻璃板;模型内部通过玻璃砖构造多组层面裂隙和垂直层面裂隙,层面裂隙隙宽为5 mm,共设7层;垂直层面裂隙隙宽为1 mm,每层设12条;裂隙网络最右边设置一条截面为3 mm×3 mm的方形管道,其下方同样铺设一条截面为3 mm×3 mm的方形管道。水头采集系统在裂隙-管道介质区安装了28只压力传感器,实时采集装置内各处的水头分布,通过信号转换系统采集数据。
泉流量通过有机玻璃量筒测量,量筒底部与压力传感器相连,圆筒内部相邻两个时刻的水头差可以通过传感器读出,进而计算出时段内的平均流量。
1.3 折算渗透系数为了建立多重空隙介质地下水流统一的控制方程,陈崇希[9]提出了折算渗透系数的概念,使不同空隙中水流的流动规律在形式上可以用线性定律表示,即
v=KLJ 。
式中:v为渗流速度,m/s;KL为折算渗透系数,m/s;J为水力坡度,无量纲。
具体来说,管道介质的折算渗透系数为

裂隙介质的折算渗透系数为
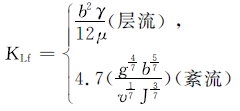
式中:d为管道内径,m;μ为动力黏度,N·s/m;γ为流体的重率,γ=ρg,其中,ρ为流体的密度,kg/m3,g为重力加速度,m/s2;f为摩擦系数,当雷诺数Re<2 300时,f=64/ Re;b为裂隙宽度,m。
本文利用Visual MODFLOW 软件,计算折算渗透系数并对不同空隙的渗透系数分别赋值,建立基于物理模型的数值模型,模拟实验室尺度的泉流量过程。
2 试验与结果分析 2.1 试验过程已有研究表明,补给雨强和泉口大小是影响泉流量过程的重要因素[7, 10, 11]。因此,试验中设置了多组不同的补给雨强和不同直径的泉口,模拟泉的出流过程,探究补给雨强和泉口大小对泉流量过程的影响规律。
一次试验开始时,首先开启补给水箱的阀门,补给雨强保持恒定。随着补给的进行,水流从装置底部的泉口排泄至量桶内。当裂隙-管道介质中水面位置稳定或水面升至装置顶端时,关闭补给水箱阀门,泉口继续排泄直至装置内的蓄水排干。整个过程中压力传感器记录压力水头,每隔1 s记录1次。然后更换不同直径的泉口出流管道,重复整个试验过程。
2.2 结果分析试验中,泉口有4种不同的内径,分别是3,4,5,7 mm。每一种泉口设置4组不同的恒定补给雨强,见表 1。通过连接圆筒的压力传感器读数计算不同时段的平均流量,平均流量系列经过滑动平均处理,点绘出泉流量过程线,见图 3。
| mL/s | ||||
| 泉口直径/ mm | 补给1 | 补给2 | 补给3 | 补给4 |
| 3 | 7.77 | 14.74 | 15.96 | 20.76 |
| 4 | 15.23 | 17.34 | 20.05 | 23.32 |
| 5 | 17.34 | 25.07 | 32.36 | 41.20 |
| 7 | 24.72 | 29.93 | 40.39 | 46.22 |
 |
| 图 3 不同条件下的泉流量过程 Fig. 3 Spring flow process in different conditions |
| |
完整的泉流量过程包括3个阶段[12]:
1)流量增大阶段
泉口刚开始出流的一段时间内,流量从0开始逐渐增大,这一阶段的流量过程受补给雨强影响较大。对于特定的泉口直径,补给雨强越大,流量的增加速率越快;对于不同泉口,在流量增加阶段的曲线上做割线,以割线斜率表示流量增加速率,通过内插,得到7,5,4和3 mm的泉口直径在补给强度25 mL/s的情况下流量增加速率分别为0.180、0.160、0.075和0.062 m/s2,泉口直径越大,流量增加速率越快。
2)流量平稳波动阶段
泉流量达到最大值后,开始在一恒定数值附近近似等振幅波动。此阶段整个装置补给与排泄基本相等,水面稳定。在泉口直径为7 mm时,4种补给雨强下平稳波动流量的均值分别为24.84,30.17,40.16,46.67 mL/s,与恒定补给雨强相差分别为0.49%,0.80%,0.57%,0.97%,非常微小,由此可以认为此阶段泉流量在恒定补给雨强这一数值附近波动。
3)流量衰减阶段
补给停止后,泉口出流流量由最大值开始衰减至0。本装置的裂隙为人工搭建,排列规则,层面裂隙和垂直层面裂隙的过流能力较大,衰减过程没有明显呈现出多个亚动态,流量衰减曲线可以用指数函数Q=Q0e-αt描述(式中:Q为泉流量;Q0为衰减开始时的流量;t为时间;α为衰减系数)。将衰减流量取自然对数点绘到直角坐标系中,各点分布在一条直线上,直线斜率即为衰减系数α。泉口直径一定时,直线近似平行,泉流量衰减系数为定值,不随补给雨强变化(图 4);泉口直径越大,泉流量衰减系数越大,衰减系数与泉口直径大致呈对数关系(图 5)。出现这一趋势的可能原因是泉口较小时对释水过程限制强烈,衰减系数对泉口的变化较敏感,随着泉口直径的增加对释水过程限制作用越来越小以至自由释水,衰减系数对泉口直径的变化越来越不敏感。
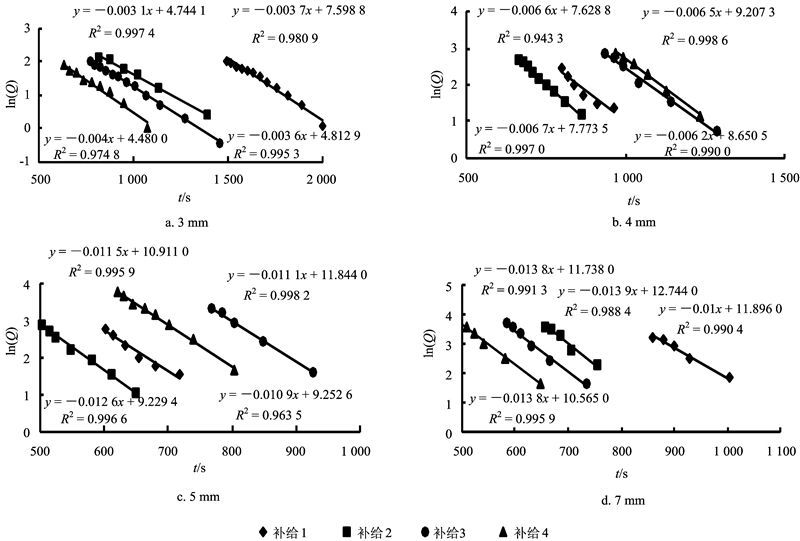 |
| 图 4 不同直径泉口条件下ln(Q)-t关系线 Fig. 4 Curves of ln(Q)-t under different vents |
| |
 |
| 图 5 泉口直径对衰减系数的影响 Fig. 5 Influences of different vents to recession coefficient |
| |
在泉流量过程的3个阶段中,衰减过程是最重要的一个方面,它集中反映了岩溶含水系统的内部空隙结构[13]。利用数值模型研究泉流量衰减过程,对定量认识泉流量动态特征有重要意义。笔者依据试验过程,利用Visual MODFLOW建立多重等效连续介质数值模型,研究泉流量衰减过程。
根据物理模型的裂隙-管道介质区域的实际大小,按照1∶1的比例建立数值模型。网格剖分为1行、26列、18层,层面裂隙、垂直层面裂隙和管道位置处的网格加密。
物理模型泉口直径设为7 mm,恒定补给流量为27.42 mL/s,装置内液面稳定时水头0.19 m,停止补给后,泉口出流量开始衰减。数值模型模拟此种情景下的泉流量衰减过程,初始水头设为0.19 m。物理模型四周为有机玻璃板,与外界无水量交换,数值模型边界条件全部设置为隔水边界。装置内有机玻璃块不透水,渗透系数、储水率和给水度几乎为0。裂隙和管道的渗透系数按照计算的折算渗透系数分别赋值。Visual MODFLOW的排水沟模块可以模拟泉流量过程[14],本文将泉口概化为一条排水沟,排水沟的水力传导系数取决于泉口直径的大小。
非均质各向同性的二维非稳定地下水水流数学模型[9, 15]为

式中:KLe为管道、层面裂隙及垂直层面裂隙的折算渗透系数(x、y、z代表不同方向),m/s;H为潜水位,m;B为含水层底板高程,m;W为单位时间单位面积上的垂向补给量,m3/s;Sy为给水度,无量纲;t为时间,s;Ω为计算区域;H0为初始水头,m;K为渗透系数,m/s;q为单宽流量,m2/s;Γ2为给定流量边界;n为二类边界外法线方向。
3.2 模型的校正与验证数值模型的校正采用“试错法”[16],主要调整了含水介质的渗透系数、给水度和排水沟的导水系数。物理模型在29.92 mL/s的恒定补给时,装置内稳定水头0.26 m,以此情景下的泉流量衰减过程对数值模型进行验证。泉流量观测值与计算值的拟合精度通常用标准化残差均方根(RMSN)来表示,标准化残差均方根值越小表示模拟结果越好。其定义是:
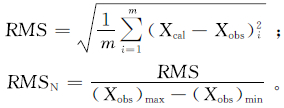
式中:RMS为均方根误差;Xcal为泉流量计算值;Xobs为泉流量观测值;m为时段数。
运行模型得到的泉流量计算值与观测值拟合较好(图 6),整个模拟期内RMSN的计算值为6.1%,表明调整后的水文地质参数取值符合实际条件,数值模型的计算结果是可靠的[17]。
 |
| 图 6 泉流量衰减过程拟合 Fig. 6 Spring flow attenuation process simulation |
| |
除了补给雨强和泉口大小,落水洞、裂隙隙宽和开采井也对岩溶含水系统泉流量有着重要影响。数值模型是研究地下水水流系统的有效工具,可以通过调整模型结构模拟不同条件下泉流量衰减过程。因此,笔者以验证后的数值模型为基础,分别研究落水洞、袭隙隙宽和开采井对泉流量衰减过程的影响。
3.3.1 落水洞对泉流量过程的影响数值模型中设置的落水洞矩形横截面边长为3.0 cm,把模型中的落水洞边长分别调整为2.0、1.0、0.5和0 cm,分别运行模型,得到不同条件下的泉流量衰减过程,见图 7。
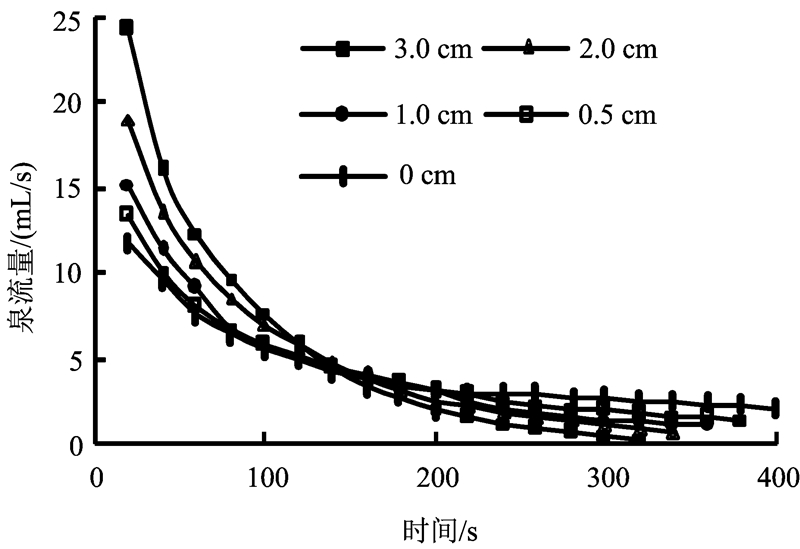 |
| 图 7 不同落水洞的泉流量衰减过程 Fig. 7 Spring flow attenuation process of different sinkhole |
| |
落水洞是岩溶含水介质内主要的集水区域和过流通道[18],其尺寸对泉流量影响较大。落水洞边长与衰减系数呈分段线性关系(图 8)。由图 8可知,落水洞边长大于1.0 cm时,泉流量较大,边长越大衰减越快,边长与衰减系数α关系线的斜率为0.002;落水洞的边长小于1.0 cm时,泉流量较小且衰减缓慢,边长与衰减系数α关系线是一条水平直线,边长对泉流量过程几乎无影响。当落水洞边长小于1.0 cm时,其直径的尺寸和裂隙隙宽相似,其对泉流量的影响远远小于较大的落水洞,因此,泉流量的变化不明显(图 7)。在西南岩溶地区,发育大量大裂隙和落水洞,随着水流对岩石的冲蚀和岩石本身的溶蚀作用,大裂隙和落水洞的直径会逐渐变大,水循环过程加剧,导致水资源流失严重,水资源保护和开发利用难度较大。3.3.2隙宽对泉流量过程的影响
 |
| 图 8 落水洞边长对衰减系数影响 Fig. 8 Influences of side length to recession coefficient |
| |
在有落水洞和无落水洞的情况下,调整数值模型层面裂隙,设置5、4、3、2和1 mm五种不同的裂隙宽度,分别运行模型,得到此种情景下的泉流量过程,如图 9所示。
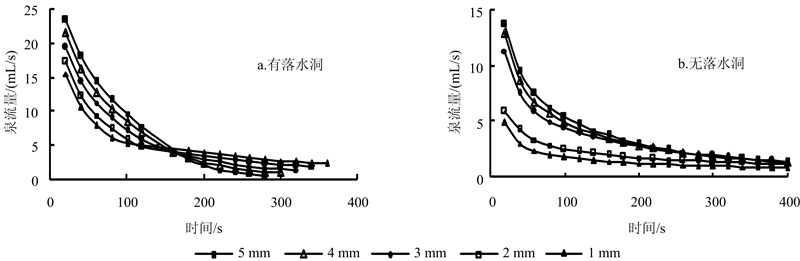 |
| 图 9 不同隙宽下的泉流量衰减过程 Fig. 9 Spring flow attenuation process of different fissure width |
| |
有落水洞时,调整层面裂隙隙宽对泉流量影响微小,这是由于落水洞是主要的储水介质,裂隙释水量与落水洞相比非常小。无落水洞时,泉流量比有落水洞时偏小:层面裂隙隙宽从5 mm变到3 mm,泉流量变化不大;层面裂隙隙宽从3 mm变到2 mm,泉流量迅速减小;这说明泉流量的减小是非线性过程。根据前人[3]的研究,大裂隙与微小裂隙的尺寸存在一个过渡区域,具有不同的水力性质。数值模型的计算结果表明2~3 mm是大裂隙和微小裂隙的过渡区,两种不同类型空隙的含水介质泉流量过程差异明显。
3.3.3 不同位置的井对泉流量过程的影响开采井通过改变地下水的水均衡状态影响岩溶区的泉流量[19],影响程度随着抽水量的变化和开采井位置的不同而不同。图 10为不同位置的开采井对泉流量衰减过程的影响关系。过程为:在数值模型落水洞处添加一开采井,设置1、3、5和7 mL/s四组不同的恒定抽水量,抽水时间100 s;然后再将开采井移到模型中间位置和泉口处,设置相同的抽水量和抽水时间,分别运行模型。由图 10可知:随着开采井的运行,整个衰减过程中泉流量变小,泉流量过程线下移,而且开采井的抽水量越大,泉流量过程线下移的幅度越大(图 10a,b);开采井在泉口附近抽水时,直接袭夺了一部分泉流量,使得泉流量衰减更快,并导致开采井停止抽水后有一个泉流量增加的过程,见图 10c。
 |
| 图 10 不同位置的开采井对泉流量衰减过程的影响 Fig. 10 Effects of different position of the pumping well on attenuation process of spring flow |
| |
衰减系数与泉流量关系如图 11所示。由图 11可见:开采井在落水洞附近或模型中间位置时,抽水量与衰减系数呈近似直线关系,开采井在泉口附近时,抽水量与衰减系数呈指数关系;在抽水量相同的情况下,泉流量衰减速率与开采井位置有关,开采井越靠近泉口,泉流量衰减越快。落水洞汇集了含水系统的大量水流,开采井在落水洞附近抽水时,对含水层的水均衡状态影响不明显,随着开采井位置远离落水洞,泉流量变化加剧。
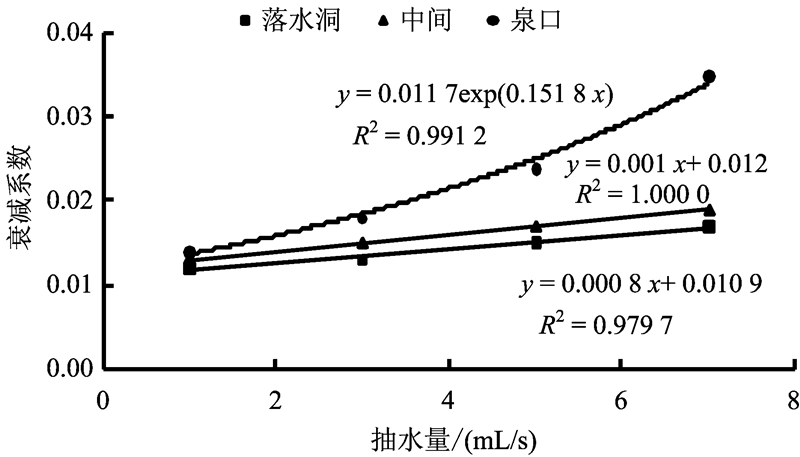 |
| 图 11 衰减系数与抽水量关系 Fig. 11 Relationship between and pumping rate |
| |
在西南岩溶地区,开发利用水资源的方式主要有人工开采地下水和地下河出口引水[20]。在落水洞发育密集的地区可以通过开采井集中开采岩溶水资源,同时地下河出口泉流量受到的影响较小,确保了地下河也能供给较为稳定的水源。在落水洞附近采取人工开采和地下河引水联合开采的方式,可以有效提高岩溶地区的水资源利用效率,提升岩溶地区水资源管理水平。
4 结论对后寨岩溶泉流域水文地质概念模型进行合理概化,建立了裂隙-管道介质物理模型,根据正交原则设计了多组试验,模拟了不同条件下的泉流量过程,得到以下主要结论:
1)泉流量的衰减系数与裂隙-管道含水介质的降雨补给无明显关系,与管道直径呈近似对数关系。
2)落水洞汇流量在泉流量中所占比例远大于裂隙释水量,主导了含水介质内的汇流方向和汇流水量。
3)泉流量随着隙宽的变小呈现非线性减小的趋势。
4)开采井与泉口和落水洞的相对位置亦是影响泉流量过程的重要因素,随着开采井向排泄区的移动,泉流量衰减过程有加速进行的趋势。
| [1] | 覃小群,朱明秋,蒋忠诚.近年来我国西南岩溶石漠化研究进展[J].中国岩溶,2006, 25(3):234-238. Qin Xiaoqun, Zhu Mingqiu, Jiang Zhongcheng.A Review on Recent Advances in Rocky Desertification in Southwest China Karst Region[J].Carsologica Sinica, 2006, 25(3):234-238. |
| [2] | 周志芳,王锦国,黄勇.裂隙介质水动力学原理[M].北京:高等教育出版社,2007. Zhou Zhifang,Wang Jinguo,Huang Yong. Theory on Dynamics of Fluids in Fractured Medium[M]. Beijing: Higher Education Press, 2007. |
| [3] | 速宝玉,詹美礼,赵坚.光滑裂隙水流模型试验及其机理初探[J].水利学报,1994(5):19-24. Su Baoyu, Zhan Meili, Zhao Jian.The Model Test of the Flow in Smooth Fracture and the Study of Its Mechanism[J]. Journal of Hydraulic Engineering, 1994(5):19-24. |
| [4] | 李文兴,王刚.岩溶管道水流的等效管束组合模拟[J].中国岩溶,1997, 16(3):40-46. Li Wenxing, Wang Gang.Combination Simulation of Equivalent Conduits of Karst Conduit Flow[J].Carsologica Sinica,1997, 16(3):40-46. |
| [5] | Salve R,Wang J S, Doughty C.Liquid-Release Tests in Unsaturated Fractures Welded Tuffs:Ⅰ:Field Investigations[J]. Journal of Hydrology, 2002, 256(1/2):60-79. |
| [6] | 沈振中,陈雰,赵坚.岩溶管道与裂隙交叉渗流特性试验研究[J].水利学报,2008,39(2):137-145. Shen Zhenzhong, Chen Fen, Zhao Jian. Experimental Study on Seepage Characteristics of the Intersection of Tubular Karst Passage and Fissure[J]. Journal of Hydraulic Engineering, 2008,39(2):137-145. |
| [7] | 董贵明,束龙仓,田娟,等. 西南岩溶地下河系统水流运动数值模型[J]. 吉林大学学报:地球科学版, 2011,41(4): 1136-1143,1156. Dong Guiming,Shu Longcang,Tian Juan,et al.Numerical Model of Groundwater Flow in Karst Underground River System,Southwestern China[J].Journal of Jilin University:Erath Science Edition, 2011,41(4): 1136-1143,1156. |
| [8] | 刘丽红,束龙仓,鲁程鹏. 基于管道流模型的岩溶含水系统降雨泉流量响应规律:以贵州后寨典型小流域为例[J]. 吉林大学学报:地球科学版, 2010,40(5), 1083-1089. Liu Lihong, Shu Longcang,Lu Chengpeng.Precipitation and Discharge Responsemechanism Based on Conduit Flow Model in Karstic Water System:Application the Houzhai Karstic Watersystem of Guizhou Province[J] Journal of Jilin University:Erath Science Edition, 2010,40(5), 1083-1089. |
| [9] | 陈崇希.岩溶管道-裂隙-孔隙三重空隙介质地下水流模型及模拟方法研究[J].地球科学:中国地质大学学报,1995,20(4):361-366. Chen Chongxi. Groundwater Flow Model and Simulation Method in Triple Media of Karstic Tube-Fissure-Pore[J]. EarthSciene:Journal of China University of Geosciences,1995,20(4):361-366. |
| [10] | 李静.洪山泉流量动态系统分析[J].水文地质工程地质,2004(2):79-82. Li Jing.Dynamic System Analysis for Flux of the Hongshan Spring[J].Hydrogeology & Engineering Geology, 2004(2):79-82. |
| [11] | 孙晨,束龙仓,鲁程鹏,等.裂隙-管道介质泉流量衰减过程试验研究及数值模拟[J].水利学报,2014,45(1):50-64. Sun Chen,Shu Longcang,Lu Chengpeng,et al.Physical Experiment and Numerical Simulation of Spring Flow Attenuation Process in Fissure-Conduit Media[J]. Journal of Hydraulic Engineering, 2014,45(1):50-64. |
| [12] | 束龙仓,陶玉飞,董贵明,等.岩溶多重介质泉水流量衰减过程的室内模拟及分析[J].工程勘察,2008(9):32-35. Shu Longcang,Tao Yufei,Dong Guiming,et al. Spring Flow Attenuation Process Simulation and Analysis of the Karst Multi-Media[J]. Geotechnical Investigation & Surveying,2008(9):32-35. |
| [13] | 程星,杨子江.影响喀斯特地下水调蓄功能的因素的探讨[J].中国岩溶,2000,19(1):54-59. Cheng Xing, Yang Zijiang.A Discussion on the Factors of Underground Water Regulation in Karst Areas[J].Carsologica Sinica, 2000,19(1):54-59. |
| [14] | Thomas E R. System and Boundary Conceptualization in Ground-Water Flow Simulation[R].Washington D C:United States Government Printing Office,2001. |
| [15] | 陈崇希,林敏.地下水动力学[M].武汉:中国地质大学出版社,1999. Chen Chongxi,Lin Min.Groundwater Dynamics[M].Wuhan:China University of Geosciences Press,1999. |
| [16] | 徐海珍,李国敏,张寿全,等.北京市平谷盆地地下水三维数值模拟及管理应用[J]. 水文地质工程地质,2011,38(2):27-34. Xu Haizhen, Li Guomin, Zhang Shouquan,et al. Development of a 3-D Numerical Groundwater Flow Model of the Pinggu Basin and Groundwater Resources Management[J].Hydrogeology & Engineering Geology, 2011, 38(2):27-34. |
| [17] | 卢文喜,李平,王福林,等.挠力河流域三维地下水流数值模拟[J]. 吉林大学学报:地球科学版, 2007,37(3): 541-545. Lu Wenxi, Li Ping,Wang Fulin,et al.Three Dimensional Numerical Simulation of Groundwater in Naolihe Watershed[J].Journal of Jilin University:Erath Science Edition, 2007,37(3): 541-545. |
| [18] | Neretnieks I,Eriksen T,Tähtinen P.Tracer Movement in a Single Fissure in Granitic Rock: Some Experimental Results and Their Interpretation[J]. Water Resource Research,1982,18(4):849-858. |
| [19] | 刘昌军,赵华,张顺福,等. 台兰河地下水库辐射井抽水过程的非稳定渗流场的有限元分析[J]. 吉林大学学报:地球科学版, 2013,43(3): 922-930. Liu Changjun,Zhao Hua,Zhang Shunfu,et al.Finite Element Analysis on Unsteady Seepage Field of Groundwater Reservoir of Tailan River During the Pumping Water of the Radiation Well[J]. Journal of Jilin University:Erath Science Edition, 2013,43(3): 922-930. |
| [20] | 梁彬,朱明秋,裴建国,等.岩溶水资源开发利用与综合治理经验:以湘西岩溶区为例[J]. 水资源保护,2007,23(2): 64-69. Liang Bin,Zhu Mingqiu,Pei Jianguo,et al.Experience on Development and Comprehensive Management of Karst Water Resources: A Case Study of Karst Regions in West Hunan[J]. Water Resources Protection, 2007,23(2): 64-69. |


