0 前言
地下水作为人类赖以生存的重要水资源,在生产、生活中发挥着重要作用。近年来,人们对浅层地下水(埋深在30 m以内)[1]资源无序的开发利用,造成大面积漏斗产生,地下水位迅速下降,并导致一系列水资源和生态环境问题,如地面沉降、地面塌陷、海水入侵等。因此,了解浅层地下水位动态特征,科学预测地下水位,对保护生态环境和实现地下水资源管理至关重要[2]。
浅层地下水位的变化是一个非常复杂的自然过程,它是地下水系统受多种激励而产生的综合效应,降水、蒸发和人工开采可视为系统的输入,地下水位埋深可视为系统的输出,输入、输出间存在复杂的非线性关系,因此不可能用简单的线性函数加以确定性描述。传统的地下水位预测方法有确定性数值模拟法[3],它虽能描述整个水文循环过程,但查明水文地质条件以及参数的获取工作量较大,且计算时间长,实际操作过于繁琐。随后,鉴于有限的数据资料且只需概括水文过程,许多学者提出随机性模型[4],其建立过程主要依赖水文气象观测资料,无需再进行专门的试验来获取参数,给大区域地下水位预报带来极大的便利,因此逐步被引入到地下水动态研究中,并发展了多种模型,如自回归综合移动平均(ARIMA)模型、时间序列模型、人工神经网络模型等[5],虽取得了一定成果,但大多还停留在起步应用和试探阶段,预报精度各异,有时甚至
笔者选择吉林西部为研究区,对比分析了ARIMA模型、BP神经网络(BP-ANN)模型和小波神经网络(WA-ANN)模型的建模过程及其模拟精度,以期了解三者在地下水动态预测中的优劣。此外,至今还没有文献将多个水文参数作为神经网络模型输入来预报浅层地下水埋深,笔者探索把降雨量、蒸发量、人工开采量和前期水位埋深作为输入,希望能为浅层地下水埋深预测提供一种新的途径。 1 方法 1.1 ARIMA模型
ARIMA模型是一种分析和预测非稳定时间序列的方法[6]。将地下水位观测值的时间序列作为一组随机序列,用相应的数学模型近似地描述出来,根据地下水位历史数值及现状预报未来。
ARIMA模型包含3个主要参数:自回归阶数(p)、差分阶数(d)和移动平均阶数(q)。其一般形式为
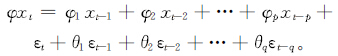
人工神经网络是一种模仿人脑信息处理机制的网络系统,具有自组织、自学习和极强的非线性能力。其非线性模式识别的特性在地下水位预测中得到广泛应用[7]。
基于BP算法的前馈型神经网络是目前使用最多也较为成功的模型之一。BP-ANN模型由输入层、隐含层和输出层组成,每层包含若干个神经元,相邻层之间通过权(wij,wjk)实现全联结,各层神经元之间无联结,网络拓扑结构如图1。为模拟神经元的非线性特征,以Sigmoid函数(S函数)作为隐含层的激活函数:

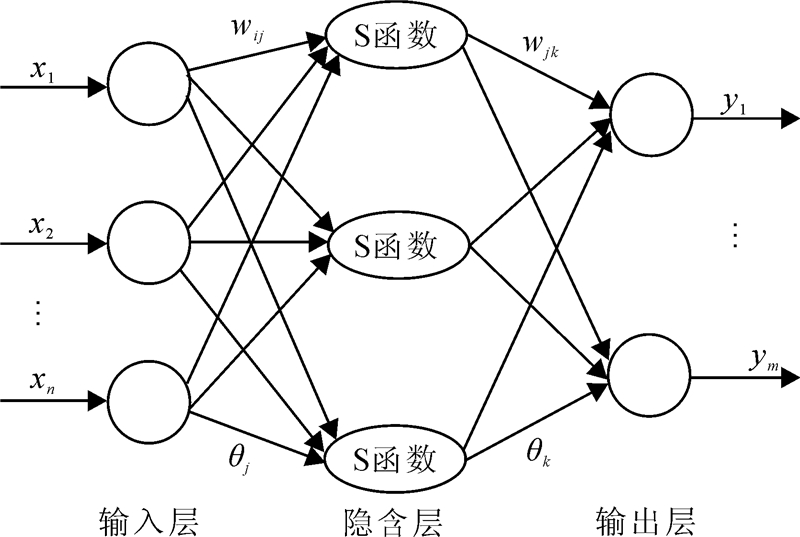 |
| xn为输入层神经元;ym为输出层神经元;ωij和ωjk为权值;θj和θk为阈值。 图 1 BP-ANN拓扑结构图Fig. 1 Experimental |
BP算法的网络学习过程包括信息的正向传播和误差的反向传播。输入信号经输入层、隐含层的神经元处理后传播到输出层给出结果;如果实际值与网络输出之间的误差不满足期望,则转入反向传播。通过修改各层神经元权值,使误差减小,然后再转入正向传播,反复迭代,直到误差达到预期精度为止。 1.3 WA-ANN模型
小波分析的基本思想类似于傅里叶变换,用一簇函数逼近某一信号,这簇函数由一个基本小波函数通过平移和伸缩构成[8]。但小波变换在处理非稳定时间序列时,能在时域和频域上同时实现局部化,并且时频窗可调,这是傅里叶变换做不到的。
WA-ANN是结合小波变换理论与人工神经网络构造而成的一种新的神经网络模型。它将隐含层中神经元的传统激发函数用小波函数来代替,充分继承了小波变换良好的时频局部化性质以及神经网络的自学习功能。本次研究的WA-ANN模型以BP神经网络拓扑结构为基础,隐含层选取的基函数为Morlet小波,数学公式为

上述分别对3种方法的原理进行了介绍,它们在适用条件、优点及缺点的对比见表1。以下将对3种方法的建模过程及模拟精度进行比较。
| 方法对比 | 适用条件 | 优点 | 缺点 |
| ARIMA模型 | 适用有历史资料的地下水动态中长期预报 | 计算过程简单,效率较高 | 以线性理论为基础,考虑问题过于简单 |
| BP-ANN模型 | 适用存在多个自变量和因变量的地下水动态短期预报 | 自组织、自学习及识别非线性模式 | 不能处理非稳定时间序列问题 |
| WA-ANN模型 | 适用有历史资料,且存在多个自变量和因变量的地下水动态中长期预报 | 自学习、自适应、识别非线性模式,提取时频特征 | 易陷入局部极小值引起震荡效应 |
对于不同模型预测效果的好坏进行评判,称为模型检验。检验的结论将直接影响人们对模型预测结果的信任程度。检验的标准主要是观测值与预测值拟合的误差,拟合误差越小,预测结果的信任程度越高[9]。本次研究选择确定性系数(R2)、均方根误差(RMSE)和Nash-Sutcliffe效率系数(NSE)对模型的预测能力进行评价。
确定性系数用于度量观测值与预测值之间的相关程度。R2值在0~1之间,越接近1,说明相关性越高;越接近0,则相关性越低。定义为
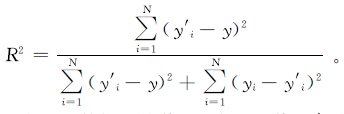
均方根误差是对预测数据可靠性的估计。RMSE越小,预测结果的可靠性越大,反之预测结果不大可靠。定义为
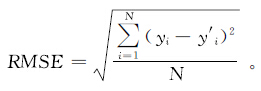
Nash-Sutcliffe效率系数用于评价水文模型的预测能力。NSE值一般为0~1,NSE越接近1,预测值和观测值拟合效果越好。定义为
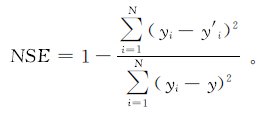
研究区位于吉林西部(123°09′E——124°22′E;44°57′N——45°46′N),处于由半湿润到半干旱气候的过渡地带,水资源较为匮乏,地下水的开发利用在工农业和生态用水中占据着重要地位。该区地下水系统总体上为一个巨大的开放系统,补给来源包括降水入渗、河流渗漏、侧向地下径流补给和灌溉入渗,排泄项包括潜水蒸发、向河流排泄、侧向径流排泄和人工开采[10],地下水位动态变化受自然因素和人为因素的双重影响。
数据来源于研究区2002年1月——2009年12月的地下水潜水动态观测资料。应用BP神经网络和小波神经网络建立地下水位预测模型前,首先确定影响地下水位变化的主要因素,根据地下水补、径、排情况,潜水补给来源主要为降水入渗,排泄途径主要为潜水蒸发和人工开采。因此,笔者设想将降水量、人工开采量、蒸发量和前期水位埋深4个因素作为输入建立地下水位预测模型。
由于统计出来的4个参数量纲不同,不能直接输入,必须进行归一化处理。为了消除量纲差异,采用线性函数转换处理原始数据,具体方法如下:

采用SPSS软件建立ARIMA模型预测地下水埋深[11],只需收集地下水埋深历史资料。将2002年1月——2008年12月的地下水埋深数据作为训练样本,2009年1月——2009年12月的地下水埋深数据作为预测样本。模型训练中,首先用差分法对时间序列进行平稳化;然后确定3个参数的取值,其中自回归阶数p和移动平均阶数q的变化范围是0~2,差分阶数d取1保证时间序列的稳定性;最后用训练好的模型进行预测。 2.2.2 BP-ANN模型
采用MATLAB R2010编写程序建立BP-ANN模型预测地下水埋深[12]。输入层节点由4个参数组成:月总降水量、月总人工开采量、月总蒸发量和前月的平均地下水埋深;输出层节点只有1个,为当月的平均地下水埋深。训练模型即由2002年2月总降水量、2月总人工开采量、2月总蒸发量和1月平均地下水埋深数据推测2002年2月平均地下水埋深,依次类推,一直到由2008年12月总降水量、12月总人工开采量、12月总蒸发量和11月平均地下水埋深数据推测2008年12月的地下水埋深。预测样本是2009年1月——2009年12月的地下水埋深数据,预测方法与训练模型相同。隐含层节点数通过误差反向传播检验进行优化和确定。本次BP-ANN采用的算法是动量的梯度下降法,迭代次数为50 000次,学习概率为0.01。 2.2.3 WA-ANN模型
采用MATLAB R2010编写程序建立WA-ANN模型预测地下水埋深[15]。首先用离散小波转换将原始地下水埋深时间序列数据分解成小波系列(DWs),DWs表示原始序列频率、时间和位置信息。为了确定分解成的小波系列数量,采用公式L=int[log(M)]求解,其中M表示时间序列数,L表示小波系列数。本次研究中,M=72,L=2,因此小波系列被确定为DW1和DW2。WA-ANN的输入层节点由4个参数的小波系列组成,输出层节点为平均地下水埋深的小波系列,隐含层节点通过误差反向传播检验确定,迭代次数为50 000次,学习概率分别为0.01和0.001。 2.3模拟结果分析
经测试,效果最好的WA-ANN模型隐含层节点数为22,BP-ANN模型隐含层节点数为8,ARIMA模型为(0,1,2),即自回归阶数为0,差分阶数为1,移动平均阶数为2。
预测期模型检验结果如表2。可知所建立的WA-ANN模型和BP-ANN模型对地下水埋深的预测结果精度均较高,并且WA-ANN模型较BP-ANN模型而言具有更高的模拟精度,而ARIMA模型的预测精度相对较低。
| 模型 | R2 | RMSE | NSE |
| WA-ANN | 0.847 | 0.283 | 0.728 |
| BP-ANN | 0.769 | 0.338 | 0.689 |
| ARIMA | 0.590 | 0.563 | 0.135 |
分别将WA-ANN模型、BP-ANN模型和ARIMA模型在吉林西部地下水埋深的预测值和观测值进行拟合,如图2所示。由图2可知,ARIMA模型在预测地下水埋深时往往小于观测水位埋深;而WA-ANN模型和BP-ANN模型的预测埋深都比较接近观测值,拟合效果较好。
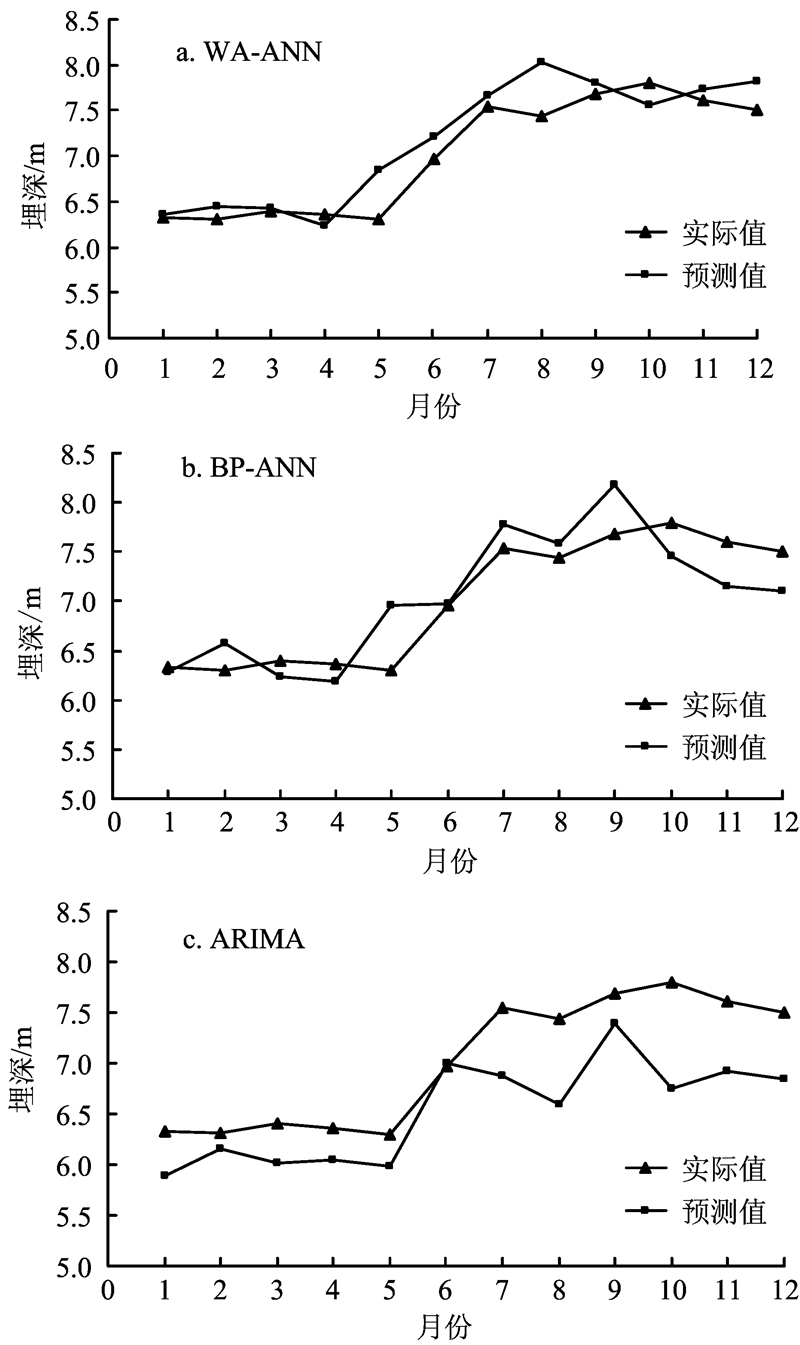 |
| 图 2 3种模型地下水位埋深预测值和观测值拟合图Fig. 2 Comparison of forecasted versus observe groundwater depth of three models |
绘制WA-ANN模型、BP-ANN模型和ARIMA模型在吉林西部地下水埋深预测值和观测值比较的散点图,如图3所示。由图3可知:WA-ANN模型的观测-预测散点在实线(观测-预测散点的趋势线)附近呈现相对密集,且实线更靠近虚线(观测-预测散点比值为1的趋势线);其次是BP-ANN模型;而ARIMA模型的观测-预测散点在实线附近比较分散,实线与虚线也相隔较远。总之,WA-ANN模型和BP-ANN模型对吉林西部地下水埋深预测结果比ARIMA模型更准确。
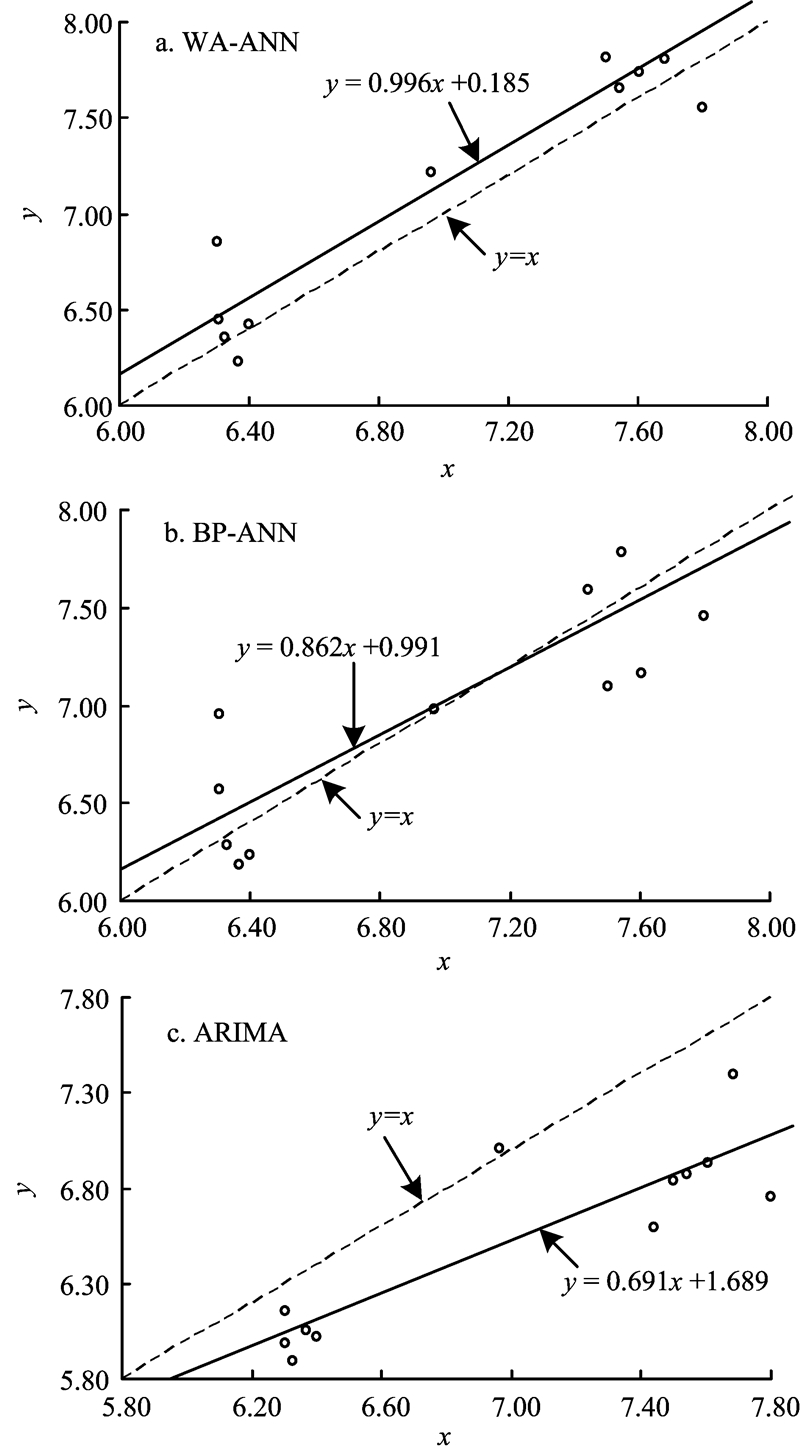 |
| 图 3 3种模型水位埋深预测值和观测值比较散点图Fig. 3 Scatterplot comparing observed and forecasted groundwater depth of three models |
1)在对吉林西部浅层地下水位动态变化规律的模拟中,相比两种ANN模型,ARIMA模型建模过程更为简单,计算效率更高;对地下水埋深预测精度从高到低依次为WA-ANN模型、BP-ANN模型、ARIMA模型。
2)WA-ANN模型既继承了小波变换良好的时频局部化特性,能充分反映非稳定时间序列变化过程的大体趋势与细节信息,又具有神经网络较强的非线性映射能力,高精度的预报结果说明它是预测地下水位动态的有效途径之一。
3)将降水量、蒸发量、人工开采量和前期水位埋深作为神经网络的输入层,适用于建立浅层地下水埋深预测模型,避免了仅用动态数据进行模拟预报的局限性,这为地下水资源管理者提供了一种新的有效的预测浅层地下水埋深方法。
4)虽然神经网络模型预测精度较高,但模型中还存在些许不足之处。在模型训练的过程中,学习概率和隐含层的神经元数需要人为定义,这使参数的设定具有一定的随机性,如何通过程序科学地、自动地设置这些参数是以后值得研究的问题。
| [1] | 安乐生,赵全升,徐颖.黄河三角洲浅层地下水位动态特征及其成因[J].环境科学与技术,2013,36(9): 51-56. An Lesheng,Zhao Quansheng,Xu Ying. Dynamic Characteristics of the Shallow Groundwater Table and Its Genesis in the Yellow River Delta[J]. Environmental Science & Technology,2013,36(9): 51-56. |
| [2] | 刘博,肖长来,梁秀娟.SOM-RBF神经网络模型在地下水位预测中的应用[J].吉林大学学报:地球科学版,2015,45(1): 225-231. Liu Bo,Xiao Changlai,Liang Xiujuan. Application of Combining SOM and RBF Neural Network Model for Groundwater Levels Prediction[J]. Journal of Jilin University: Earth Science Edition,2015,45(1): 225-231. |
| [3] | 高翠萍,杜新强,郭中小,等.桦南县地下水数值模拟研究[J].人民黄河,2014,36(1): 78-81. Gao Cuiping,Du Xinqiang,Guo Zhongxiao,et al. Application of Visual MODFLOW in Groundwater Numerical Simulation of Huanan County[J]. Yellow River,2014,36(1): 78-81. |
| [4] | 杨耀,张枝梅,张国晓.随机模型在地下水资源评价中的应用研究[J].北方环境,2013,29(4): 80-84. Yang Yao,Zhang Zhimei,Zhang Guoxiao. Application Study on the Stochastic Models in Groundwater Resource Evaluation[J]. Northern Environment,2013,29(4): 80-84. |
| [5] | 卢文喜,杨磊磊,龚磊,等.基于时间序列分析改进法的地下水位动态预报:以吉林省桦甸市为例[J].吉林大学学报:地球科学版,2012,42(1): 367-372. Lu Wenxi,Yang Leilei,Gong Lei,et al. Dynamic Forecasting of Groundwater Table Based on the Improved Time Series Analysis Method: A Case Study of Huadian City,Jilin Province,China[J]. Journal of Jilin University: Earth Science Edition,2012,42(1): 367-372. |
| [6] | 李娜,周维博,董起广.基于ARIAM模型的灌区地下水动态预报[J].人民长江,2014,45(9): 43-47. Li Na,Zhou Weibo,Dong Qiguang. Groundwater Dynamic Prediction in Irrigation Area Based on ARIAM Model[J]. Yangtze River,2014,45(9): 43-47. |
| [7] | 张斌,刘俊民.基于BP神经网络的地下水动态预测[J].水土保持研究,2012,19(5): 235-237. Zhang Bin,Liu Junmin. Prediction of Groundwater Dynamics Based on the BP Neural Network[J]. Research of Soil and Water Conservation,2012,19(5): 235-237. |
| [8] | 严其芳,王卫光,王志平,等.小波网络耦合模型在地下水位动态预测中的应用[J].水电能源科学,2012,30(5): 16-20. Yan Qifang,Wang Weiguang,Wang Zhiping,et al. Application of Wavelet Network Coupling Model to Groundwater Level Forecasting[J]. Water Resources and Power,2012,30(5): 16-20. |
| [9] | Jan A. A Wavelet Neural Network Conjunction Model for Groundwater Level Forecasting[J]. Journal of Hydrology,2011,407: 28-40. |
| [10] | 陈社明.吉林西部浅层地下水系统对旱改水工程的响应研究[D]. 长春: 吉林大学,2013. Chen Sheming. Response of Shallow Groundwater System to Dryland Changed into Paddy Field Project in Western of Jilin Province[D]. Changchun: Jilin University,2013. |
| [11] | 杜强,贾丽艳.SPSS统计分析从入门到精通[M].2版. 北京: 人民邮电出版社,2009. Du Qiang,Jia Liyan. SPSS Statistical Analysis from Entry to the Master[M]. 2nd ed. Beijing: People Post Press,2009. |
| [12] | 傅荟璇,赵红.MATLAB神经网络应用设计[M]. 2版.北京:机械工业出版社,2010. Fu Huixuan,Zhao Hong. Application and Design of Neural Network in MATLAB[M]. 2nd ed. Beijing: Machinery Industry Press,2010. |



