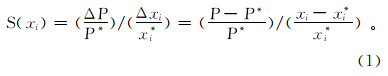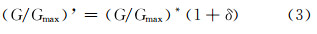在场地地震反应分析中,包括动剪切模量比和阻尼比在内的土动力学参数对土层地震反应计算结果有重要的影响[1]。吕悦军等[2]曾对渤海海底常见土类动剪切模量比和阻尼比进行了试验研究,并得到各类土的动剪切模量比和阻尼比随剪应变变化的曲线。荣棉水等[3, 4, 5]曾针对渤海海域软表层土动剪切模量比和阻尼比展开专门研究,给出了其统计均值曲线并研究了渤海海域厚软表层对设计地震动参数确定的影响,在此基础上提出了适用于海域软弱场地的非线性土层地震反应分析方法。土动力学参数值的取值具有较大的不确定性。孙锐等[6]曾利用中国42个城市和地区的588组土样实验数据统计分析了常规土类动剪切模量比等参数取值的不确定性,给出了动剪切模量比曲线的变异系数,并指出对动力学参数不确定性的研究具有重要的理论意义和工程应用价值。曾有学者对动力学参数不确定性的影响进行了定性的研究。朱国祥[7]对若干土类的动力学参数进行了敏感性分析。刘红帅等[8]定性地研究了单层均质土动剪切模量比变化对土层地表反应谱的影响,得到了一些有价值的结论。陈国兴等[9]定性地研究了土动力学参数变异性对深软场地地表峰值加速度和反应谱的影响。陈红娟等[10]定性地分析了黏土动剪切模量比的不确定性对反应谱的影响。孙锐等[11]曾研究了动剪切模量比和剪切波速对地震动的影响,并以对地表加速度反应谱的影响为标准定量分析了动剪切模量比变化与剪切波速变化的对等关系,并建立了等价关系式。总之,目前对动剪切模量比不确定性影响的研究很多,但多是定性的,而且针对海域场地的研究很少。渤海有丰富的油气资源[12, 13, 14],包括海洋平台在内的海洋工程建设项目日益增多。笔者利用地震安全评价工作中积累的众多渤海海域场地模型,对动剪切模量比对反应谱的影响进行定量计算,并从中选取计算结果较典型的3个场地进行对照分析,以期对渤海海域场地地震反应分析工作的开展起到一定的作用。 1 分析方法 1.1 场地地震反应分析方法
场地地震反应分析采用一维等效线性法。等效线性法是将非线性土层地震反应问题简化为线性土层地震反应问题的一种方法。其基本思想是:在真实地震波穿过土层时,土体承受不规则的循环载荷,在应力应变平面上非线性土层地震反应的应力应变关系呈现复杂的回线图形[15]。作为一种简化,使用一条等效的稳态回线近似地表示所有回线的平均关系,这种简化的方法就是等效线性法。相应的程序有LSSRLI、DENSOR、SHAKE91等,笔者使用中国地震局推荐的标准程序LSSRLI,该程序已被广泛地应用到我国地震安全性评价工作中。 1.2 敏感性分析方法
敏感性分析是系统分析理论中分析系统稳定性的一种方法。设系统P由n个因素决定,P=f(x1,x2,…,xn)。在某一基准输入X*={ x*1,x*2,…,x* n}下,系统基准状态为P*。令各因素在各自可能的范围内变动,分析这些变动造成的系统特性P偏离基准状态P*的趋势和程度,这种分析方法称为敏感性分析[16]。无量纲的敏感度等于系统特性P的相对偏差与因素xi的相对偏差之比,其定义公式为
式中:S(xi)为敏感度函数;ΔP为系统特性P的相对偏差;Δxi为因素xi的相对偏差。在土层地震反应分析中,场地的加速度反应谱有众多的影响因素,包括地震动输入情况、土层厚度、剪切波速、动剪切模量比、阻尼比等,本文只探讨反应谱对动剪切模量比的敏感度。首先,以实测动剪切模量比曲线的拟合值作为基准输入,以此输入下计算出的地表反应谱作为基准反应谱;然后,赋予动剪切模量比一个相对偏差,求得此时反应谱相对基准反应谱的相对偏差;最后,两者相除便可求出反应谱对动剪切模量比的敏感度。 2 数值实验方案
为了研究反应谱对动剪切模量比的敏感度,需要在控制其他量不变的条件下,对土层的动剪切模量比作出不同程度的改变。在土层地震反应分析中,动剪切模量比不是单独的一个值,而是一条随剪应变变化的曲线(G/Gmax-γ曲线),经验公式为
式中:G/Gmax为动剪切模量比;γ为剪应变;γr为参考应变。为定量描述动剪切模量比曲线的变动幅度,笔者以剪应变为10-3处的动剪切模量比的变动幅度代表整条曲线的变动幅度。这样选择是因为要兼顾曲线形状的控制与曲线变化的幅度。在数值实验中,首先对各场地建立场地模型,每个场地模型中每层土依次按相对偏差±1%、±3%、±5%、…、±21%计算出新的动剪切模量比;随后用等效线性法计算基准反应谱及动剪切模量比变化后的反应谱;最后得到场地的反应谱对动剪切模量比的敏感度。为表述方便,把通过增大动剪切模量比而得到反应谱敏感度的方案记为方案1;把通过减小动剪切模量比而得到反应谱敏感度的方案记为方案2;把小震、中震、大震3种概率水准依次记为概率水准1、概率水准2、概率水准3。 2.1 输入地震动时程
输入地震动峰值分别按50 a超越概率63%、10%、2%选取,依次对应小震、中震、大震。根据本文使用的典型钻孔所在位置的地震危险性分析结果,3种概率水准对应的峰值加速度分别取为39、185、353 Gal。其时程见图 1。
 |
| 图 1 输入加速度时程 Fig. 1 Inputted acceleration time history |
| |
笔者选取3个计算结果较典型的场地做重点分析。这3个场地分别分布于辽东湾海域、渤中海域和岐口附近海域,场地分层情况见表 1表 3。与渤海的大多数场地一样,3个场地都属于二类场地。
| 序号 | 土层 | 层厚/ m | 密度/ (g/cm3) | 波速/ (m/s) |
| 1 | 松散的粉砂质细砂 | 3.8 | 2.10 | 132.1 |
| 2 | 非常软的砂质黏土 | 2.0 | 1.94 | 155.0 |
| 3 | 非常软软的粉质黏土 | 5.2 | 1.94 | 185.6 |
| 4 | 非常软软的粉质黏土 | 5.1 | 1.95 | 206.2 |
| 5 | 中密的粉质细砂 | 3.7 | 2.07 | 222.1 |
| 6 | 硬的粉质黏土 | 4.6 | 2.06 | 271.7 |
| 7 | 坚硬的粉质黏土 | 2.8 | 2.10 | 258.8 |
| 8 | 密实的砂质粉土 | 4.0 | 2.10 | 259.0 |
| 9 | 非常密实的粉质细砂 | 6.9 | 2.07 | 275.0 |
| 10 | 坚硬的粉质黏土 | 5.1 | 2.04 | 314.2 |
| 11 | 非常密实的细砂 | 6.0 | 2.07 | 325.6 |
| 12 | 非常密实的细砂 | 5.9 | 2.07 | 339.9 |
| 13 | 坚硬非常坚硬的粉质黏土 | 5.0 | 1.98 | 317.3 |
| 14 | 坚硬非常坚硬的粉质黏土 | 5.2 | 2.05 | 336.2 |
| 15 | 非常密实的砂质粉土 | 3.8 | 1.99 | 357.3 |
| 16 | 非常密实的粘质粉土 | 5.0 | 1.99 | 365.0 |
| 17 | 非常坚硬的粉质黏土 | 6.2 | 1.98 | 328.6 |
| 18 | 非常坚硬的粉质黏土 | 6.1 | 2.04 | 404.6 |
| 19 | 非常密实的粉质细砂 | 4.4 | 2.05 | 392.0 |
|
20 | 密实的砂质粉土和 非常坚硬的粉质黏土互层 | 6.2 | 2.02 | 358.2 |
| 21 | 非常密实的粉质细砂 | 3.1 | 2.12 | 398.5 |
| 22 | 非常坚硬的粉质黏土 | 9.9 | 2.18 | 517.2 |
| 序号 | 土层 | 层厚/ m | 密度/ (g/cm3) | 波速/ (m/s) |
| 1 | 非常软软的粉质黏土 | 5.3 | 1.96 | 125.3 |
| 2 | 中密实的粉砂和砂质粉砂 | 3.8 | 1.95 | 149.8 |
| 3 | 硬的粉质黏土 | 1.2 | 2.01 | 185.9 |
| 4 | 中密实密实的粉砂 | 6.4 | 2.11 | 234.2 |
| 5 | 密实的粉质细砂-细砂 | 4.5 | 2.14 | 269.0 |
| 6 | 硬的粉质黏土 | 4.9 | 2.05 | 240.0 |
| 7 | 密实的粉砂粉质细砂 | 5.1 | 2.10 | 258.0 |
|
8 | 非常硬的粉质黏土和 非常密实的粉砂互层 | 6.1 | 2.05 | 276.1 |
| 9 | 非常密实的粉质细砂 | 9.1 | 2.09 | 344.5 |
| 10 | 非常硬的粉质黏土 | 2.7 | 2.15 | 357.0 |
| 11 | 非常密实的粉砂 | 4.6 | 2.04 | 321.0 |
| 12 | 非常硬坚硬的粉质黏土 | 6.0 | 2.11 | 346.5 |
| 13 | 非常密实的砂质粉砂 | 2.9 | 2.02 | 345.0 |
|
14 | 坚硬的粉质黏土和非常密实 的粉砂、砂质粉砂叠层 | 4.6 | 2.02 | 355.0 |
| 15 | 非常密实的粉砂 | 3.7 | 2.02 | 366.4 |
| 16 | 坚硬的粉质黏土 | 6.2 | 2.10 | 346.1 |
| 17 | 坚硬的粉质黏土 | 1.6 | 2.15 | 380.3 |
| 18 | 坚硬的粉质黏土 | 7.3 | 2.08 | 384.9 |
| 19 | 坚硬的粉质黏土 | 1.4 | 2.01 | 358.1 |
| 20 | 坚硬的粉质黏土 | 8.3 | 2.22 | 531.5 |
| 21 | 非常密实的粉质细砂 | 1.7 | 2.06 | 410.0 |
| 22 | 坚硬的粉质黏土 | 1.7 | 2.22 | 500.0 |
| 23 | 非常密实的粉砂 | 2.8 | 2.06 | 415.0 |
| 24 | 坚硬的粉质黏土 | 2.9 | 2.23 | 516.6 |
| 25 | 非常密实的粉质细砂和细砂 | 10.3 | 2.06 | 440.7 |
| 26 | 非常密实的粉砂 | 4.0 | 2.09 | 428.3 |
| 27 | 坚硬的粉质黏土 | 1.3 | 2.21 | 516.2 |
| 序号 | 土层 | 层厚/ m | 密度/ (g/cm3) | 波速/(m/s) |
| 1 | 非常软稍硬的粉质黏土 | 8.9 | 1.90 | 125.1 |
| 2 | 稍硬的粉质黏土 | 4.8 | 1.90 | 150.0 |
| 3 | 中密实的粉土 | 1.0 | 2.10 | 217.6 |
| 4 | 硬的粉质黏土 | 4.5 | 1.93 | 180.0 |
| 5 | 密实的砂质粉土 | 2.0 | 2.12 | 256.3 |
| 6 | 密实的细砂和粉质细砂 | 9.8 | 2.14 | 287.3 |
| 7 | 硬的粉质黏土和黏土 | 6.1 | 1.93 | 222.6 |
| 8 | 硬的粉质黏土和黏土 | 6.1 | 1.89 | 236.3 |
| 9 | 密实的粉土 | 7.5 | 2.20 | 317.9 |
| 10 | 密实的粉质细砂 | 3.0 | 2.20 | 330.0 |
| 11 | 非常硬的粉质黏土 | 5.3 | 2.08 | 313.4 |
| 12 | 非常硬的粉质黏土 | 6.8 | 2.08 | 332.9 |
| 13 | 密实的粉土 | 4.2 | 2.17 | 370.4 |
| 14 | 密实的粉土 | 5.5 | 2.12 | 389.9 |
| 15 | 非常密实的粉质细砂 | 3.1 | 2.12 | 390.0 |
| 16 | 密实的粉土 | 2.8 | 2.12 | 390.0 |
| 17 | 坚硬的黏土 | 3.0 | 2.10 | 350.0 |
|
18 | 密实非常密实的 砂质粉土和粉土 | 8.2 | 2.13 | 394.5 |
| 19 | 非常硬的粉质黏土 | 3.0 | 2.10 | 410.0 |
| 20 | 密实非常密实的粉质细砂 | 6.2 | 2.07 | 411.6 |
| 21 | 非常硬坚硬的粉质黏土 | 6.2 | 2.16 | 463.7 |
| 22 | 非常硬坚硬的粉质黏土 | 7.0 | 2.12 | 445.8 |
| 23 | 非常硬坚硬的粉质黏土 | 5.3 | 2.16 | 455.5 |
本文所采取的生成不同相对偏差的动剪切模量比的方法,是先对原始动剪切模量比曲线按照式(2)进行拟合,求得参数γr,将拟合后的曲线定为基准动剪切模量比曲线;然后计算出应变γ=10-3处的值(G/Gmax)*,并利用公式
对该值赋予一个相对偏差δ,得到新的值(G/Gmax)’;再将γ=10-3和(G/Gmax)’代入式(2)求出新的参数值γ’r,即得到了赋予相对偏差后的G/Gmax-γ曲线(图 2)。其中,图 2a是对某条动模量比曲线增大1%至21%后的结果,图 2b是对该条动模量比曲线减小1%至21%后的结果。  |
| 图 2 生成的场地1中某层土的动剪切模量比曲线 Fig. 2 Generated dynamic shear modulus ratio curves of a layer in site 1 |
| |
实验首先计算得到了3个场地在2种方案中3种概率水准下的反应谱曲线,然后进一步计算得到了各反应谱相对基准反应谱的相对偏差曲线,见图 3图 8。±1% ±21%分别表示在应变为10-3处的动剪切模量比增大或减小1%~21%。下同。
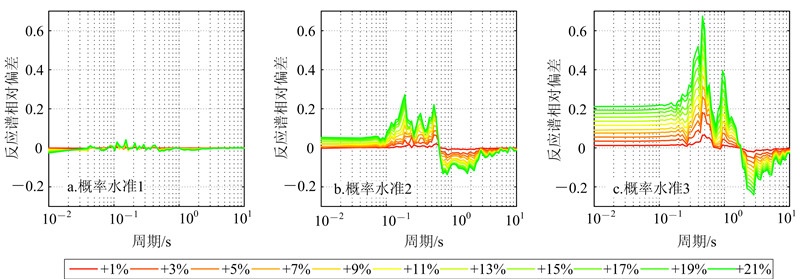 |
| 图 3 场地1在方案1中算得的反应谱相对偏差曲线 Fig. 3 Relative deviation curves of response spectra of site 1 in plan 1 |
| |
通过图 3与图 4、图 5与图 6、图 7与图 8的对比,可以看出动剪切模量比的放大与减小对反应谱的影响是不对称的。当动剪切模量比曲线增大或减小1%~21%后,不同周期处的反应谱值呈现不同程度的增大或减小,各条反应谱相对偏差曲线呈现“层叠”式分布。3个场地基准反应谱的特征周期见表 4。特征周期的计算公式[17] 为
式中:Tg为反应谱特征周期;vmax为峰值速度;amax为峰值加速度。在基准反应谱的特征周期附近,各条反应谱相对偏差曲线的变化呈现统一的规律,即存在一个零点,这个点即各反应谱相对基准反应谱增大和减小的转变点。通过零点左右反应谱相对偏差的正负可以推出:当动剪切模量比增大时,相对于基准反应谱,零点左侧的反应谱增大,右侧的减小;当动剪切模量比减小时,规律则相反。 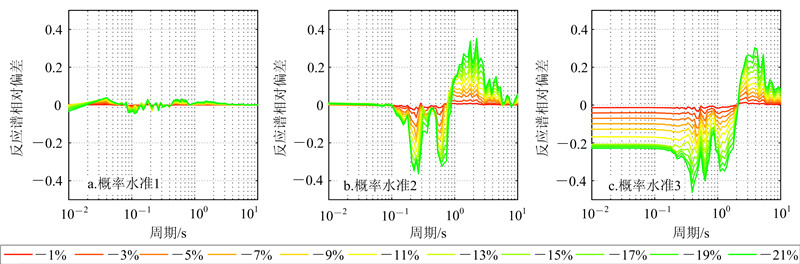 |
| 图 4 场地1在方案2中算得的反应谱相对偏差曲线 Fig. 4 Relative deviation curves of response spectra of site 1 in plan 2 |
| |
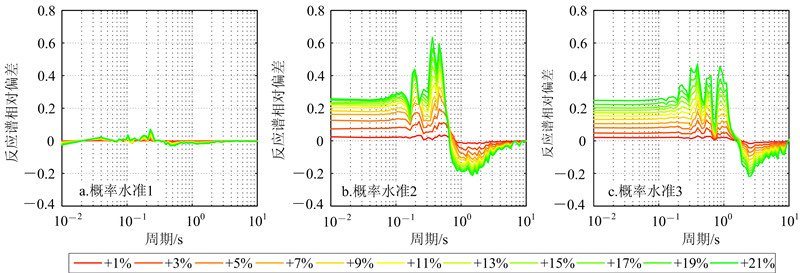 |
| 图 5 场地2在方案1中算得的反应谱相对偏差曲线< Fig. 5 Relative deviation curves of response spectra of site 2 in plan 1 |
| |
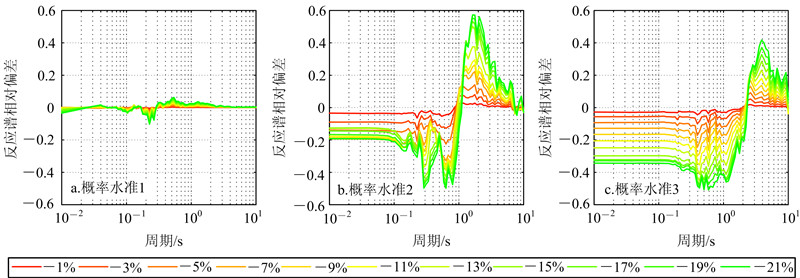 |
| 图 6 场地2在方案2中算得的反应谱相对偏差曲线 Fig. 6 Relative deviation curves of response spectra of site 2 in plan 2 |
| |
 |
| 图 7 场地3在方案1中算得的反应谱相对偏差曲线 Fig. 7 Relative deviation curves of response spectra of site 3 in plan 1 |
| |
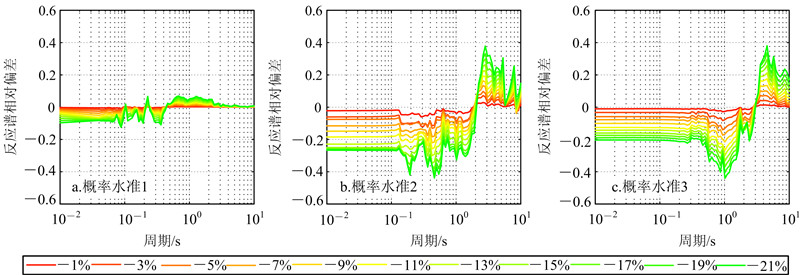 |
| 图 8 场地3在方案2中算得的反应谱相对偏差曲线 Fig. 8 Relative deviation curves of response spectra of site 3 in plan 2 |
| |
| 场地编号 | 特征周期/s | ||
| 概率水准1 | 概率水准2 | 概率水准3 | |
| 1 | 0.33 | 0.57 | 1.42 |
| 2 | 0.33 | 0.76 | 1.26 |
| 3 | 0.43 | 1.31 | 1.37 |
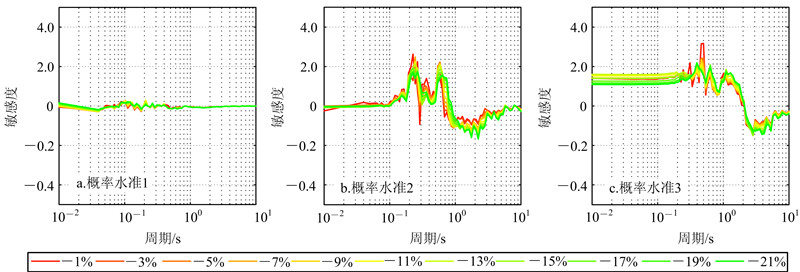
在求得反应谱相对偏差曲线之后,笔者计算得到了各条反应谱的敏感度曲线。鉴于篇幅的限制,文中只给出了场地1的曲线,如图 9和图 10所示。可以看出,在同一个方案同一种概率水准下,不同动剪切模量比对应的敏感度曲线相差不大,故笔者进一步对这些曲线求取了均值,绘成敏感度均值曲线。2个方案中3个场地的敏感度均值曲线见图 11。
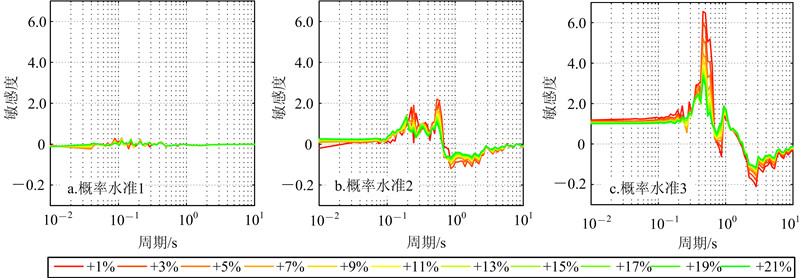 |
| 图 9 场地1在方案1中反应谱敏感度曲线 Fig. 9 Sensitivity curves of response spectra of site 1 in plan 1 |
| |
 |
| 图 10 场地1在方案2中反应谱敏感度曲线 Fig. 10 Sensitivity curves of response spectra of site 1 in plan 2 |
| |
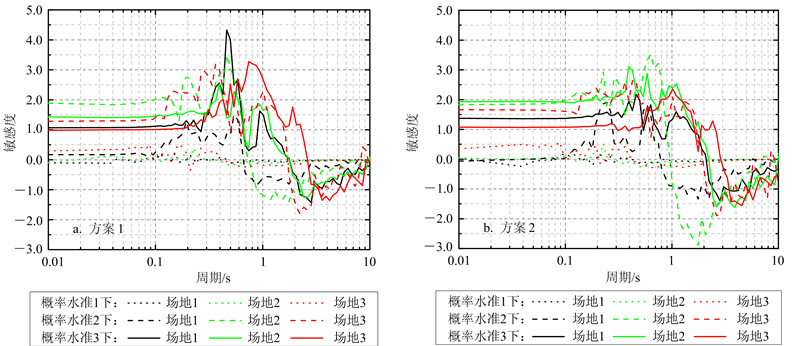 |
| 图 11 3个场地在两种方案下反应谱的敏感度均值曲线 Fig. 11 Response spectra’s mean sensitivity curves of three sites in two plans |
| |
由图 11可以得出,对同一个场地、不同概率水准的地震动输入下,反应谱的敏感度曲线相差很大。但总体上说,反应谱敏感度均值曲线的变化有一定的规律。首先,在基准反应谱的特征周期附近,反应谱的敏感度均值曲线存在一个零点。根据公式(1),可以推知这一零点是反应谱相对基准反应谱增大与减小的转变点。其次,就曲线波形而言,在较小周期时(0.01~0.10 s,对应规准反应谱上升段),曲线较平稳;在较大周期时(0.10 s~零点,对应规准反应谱平台段),曲线先升高后降低,且波动较大;在长周期时(零点~10.00 s,对应规准反应谱下降段),曲线先降低后升高,慢慢趋近于0。最后,就敏感度的取值而言:位于零点左侧的反应谱平台段的敏感度最高,在概率水准2和3下,其值基本上分布在1.0~3.0,个别达到3.0以上;反应谱下降段的敏感度绝对值次之,在靠近零点的位置敏感度的绝对值达到最大,在概率水准2和3下,其值达到1.0以上,然后随着周期值的增大敏感度绝对值减小;反应谱上升段的敏感度的分布平稳,在概率水准2和3下,其值多分布在1.0~2.0。 4 结论
本文引入统计分析中参数敏感度的概念,对土层地震反应分析中土体动剪切模量的影响进行了定量分析。通过渤海海域典型场地的众多数值实验和分析,得出结论如下:
1)动剪切模量比的增大与减小对反应谱的影响是不对称的。
2)在动剪切模量比曲线增大(减小)后,在基准反应谱的特征周期附近,存在一个反应谱相对于基准反应谱由增大转变为减小(由减小转变为增大)的转变点。
3)反应谱的敏感度与输入地震动大小有关,反应谱平台段对动剪切模量比的敏感度最高。在概率水准2和3下,其值基本上分布在1.0~3.0。
4)反应谱下降段的敏感度绝对值随着周期的增大先迅速增大,在转变点右侧附近达到最大值,概率水准2和3下其值达1.0以上,然后缓慢减小,最终趋于0。
5)反应谱上升段的敏感度分布平稳,在概率水准2和3下,其值多分布在1.0~2.0。以上结论对渤海海域的场地有适用性,对其他地区的场地有待进一步证明。
| [1] | 兰景岩, 刘红帅, 吕悦军, 等. 表层土剪切波速的不确定性对地表设计谱平台值的影响[J]. 吉林大学学报: 地球科学版, 2012, 42(3): 772-778. Lan Jingyan, Liu Hongshuai, Lü Yuejun, et al. Effects of Uncertainties of Shear Wave Velocity of Soil Surface Layer on Platform Value of Surface Design Response Spectra[J]. Journal of Jilin University:Earth Science Edition, 2012, 42(3):772-778. |
| [2] | 吕悦军, 唐荣余, 沙海军. 渤海海底土类动剪切模量比和阻尼比试验研究[J]. 防灾减灾工程学报, 2003, 23(2): 35-42. Lü Yuejun, Tang Rongyu, Sha Haijun. Experimental Study on Dynamic Shear Modulus Ratio and Damping Ratio of the Soils of Bohai Seafloor[J]. Journal of Disaster Prevention and Mitigation Engineering, 2003,23(2):35-42. |
| [3] | 荣棉水,李红光,李小军,等. Davidenkov模型对海域软土的适用性研究[J]. 岩土工程学报, 2013, 35(增刊2): 596-600. Rong Mianshui,Li Hongguang, Li Xiaojun,et al. Applicability of Davidenkov Model for Soft Soils in Sea Areas[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(Sup.2): 596-600. |
| [4] | 荣棉水,李小军,卢滔,等. 对含厚软表层海域工程场地设计地震动参数的一点建议[J]. 地震学报,2013,35(2):262-271. Rong Mianshui, Li Xiaojun, Lu Tao, et al. Suggestion on Determination of Design Ground Motion Parameters for Offshore Engineering Sites with Deep Soft Suface Layers[J]. Acta Seismologica Sinica,2013,35(2):262-271. |
| [5] | 荣棉水,卢滔,李小军,等. 一种基于动态骨架曲线的土层时域积分方法及其验证[J].应用基础与工程科学学报, 2013, 21(1):78-89. Rong Mianshui, Lu Tao, Li Xiaojun et al. A Direct Time-Domain Integral Method Based on Dynamic Skeleton Curve Constitutive Model and Its Verification[J]. Journal of Basic Science and Engineering, 2013, 21(1):78-89. |
| [6] | 孙锐, 陈红娟, 袁晓铭. 土的非线性动剪切模量比和阻尼比不确定性分析[J]. 岩土工程学报, 2010, 32(8): 1228-1235. Sun Rui, Chen Hongjuan, Yuan Xiaoming. Un-certainty of Non-Linear Dynamic Shear Modular Ratio and Damping Ratio of Soils[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(8): 1228-1235. |
| [7] | 朱国祥. 土层地震反应分析中不同参数的敏感性分析[J]. 工程抗震, 2004, 100(3): 27-32. Zhu Guoxiang. Sensitivity of Different Parameters Applied in Seismic Analysis of Multi-Layer Soil Models[J]. Earthquake Resistant Engineering, 2004, 100(3): 27-32. |
| [8] | 刘红帅, 薄景山, 吴兆营, 等. 土体参数对地表加速度峰值和反应谱的影响[J]. 地震研究, 2005, 28(2): 167-171. Liu Hongshuai, Bo Jingshan, Wu Zhaoying, et al. Effects of Soil Parameters on Ground Surface Acceleration Peak and Response Spectra[J]. Journal of Seismological Research, 2005, 28(2): 167-171. |
| [9] | 陈国兴, 刘雪珠, 王炳辉. 土动力参数变异性对深软场地地表地震动参数的影响[J]. 防灾减灾工程学报, 2007, 27(1): 1-10. Chen Guoxing, Liu Xuezhu, Wang Binghui. Effect of Variability of Soil Dynamic Parameters on Ground Motion Parameters for Deep Soft Sites[J]. Journal of Disaster Prevention and Mitigation Engineering, 2007, 27(1): 1-10. |
| [10] | 陈红娟, 孙锐, 袁晓铭, 等. 不同概率水准下黏土动剪切模量比对地震动的影响[C]//第八届全国地震工程学术会议论文集:Ⅰ. 重庆:重庆大学, 2010:114-116. Chen Hongjuan, Sun Rui, Yuan Xiaoming, et al. Effects of Clay's Dynamic Shear Modulus Ratio on Ground Motion Under Different Probability Level[C]//8th National Earthquake Engineering Conference Proceedings:I. Chongqing :Chongqing University, 2010:114-116. |
| [11] | 孙锐, 袁晓铭, 刘晓键. 动剪切模量比与剪切波速对地震动影响及等量关系研究[J]. 岩土工程学报, 2009,31(8): 1267-1274. Sun Rui, Yuan Xiaoming, Liu Xiaojian. Effects of Dynamic Shear Modulus Ratio and Velocity on Surface Ground Motion and Their Equivalent Relations[J]. Chinese Journal of Geotechnical Engineering, 2009,31(8): 1267-1274. |
| [12] | 王蛟, 姜在兴, 陈世悦. 渤海湾盆地车镇凹陷古近系层序地层与隐蔽油气藏[J]. 吉林大学学报: 地球科学版, 2005, 35(2): 163-169. Wang Jiao, Jiang Zaixing, Chen Shiyue. Sequence Stratigraphy and Subtle Hydrocarbon Reservoir of Paleogene in Chezhen Sag, Bohai Bay Basin[J]. Journal of Jilin University:Earth Science Edition, 2005, 35(2): 163-169. |
| [13] | 张莉, 朱筱敏, 钟大康, 等. 惠民凹陷古近系砂岩储层物性控制因素评价[J]. 吉林大学学报 :地球科学版, 2007, 37(1):105-111. Zhang Li, Zhu Xiaomin, Zhong Dakang, et al. Evaluation on Controlling Factors of Paleogene Sandstone Reservoir in Huimin Sag[J]. Journal of Jilin University:Earth Science Edition, 2007, 37(1):105-111. |
| [14] | 黄传炎, 王华, 吴永平, 等. 歧口凹陷第三系层序格架下的油气藏富集规律[J]. 吉林大学学报: 地球科学版, 2010,40 (5): 986-995. Huang Chuanyan, Wang Hua, Wu Yongping, et al. Analysis of the Hydrocarbon Enrichment Regularity in the Sequence Stratigraphic Framework of Tertiary in Qikou Sag[J]. Journal of Jilin University:Earth Science Edition, 2010,40(5): 986-995. |
| [15] | 廖振鹏,李小军.地表土层地震反应的等效线性化解法[M]//地震小区划: 理论与实践.北京: 地震出版社, 1989: 141-151. Liao Zhenpeng, Li Xiaojun. Equivalent Linear Method for Solving Surface Soil Seismic Response Problem[M]//Seismic Microzonation: Theory and Practice.Beijing: Seismological Press, 1989: 141-151. |
| [16] | 章光, 朱维申. 参数敏感性分析与试验方案优化[J]. 岩土力学, 1993, 14(1): 51-57. Zhang Guang, Zhu Weishen. Parameter Sensitivity Analysis and Optimizing for Test Programs[J]. Rock and Soil Mechanics, 1993, 14(1): 51-57. |
| [17] | 廖振鹏,李大华.设计地震反应谱的双参数标定模型[M]//地震小区划: 理论与实践.北京:地震出版社, 1989: 196-206. Liao Zhenpeng, Li Dahua. Two-Parameter Calibration Model for Seismic Response Spectrum[M]//Seismic Microzonation: Theory and Practice.Beijing: Seismological Press, 1989: 196-206. |