Download PDF  
文章快速检索  
  高级检索
引用本文
吴琼, 李树文, 李宏卿, 甄佳宁, 李磊, 杨国东. 地面重力数据结合GPS/水准数据精化兴城物探实验区大地水准面[J]. 吉林大学学报(地球科学版), 2015, 45(2): 655-662
Wu Qiong, Li Shuwen, Li Hongqing, Zhen Jianing, Li Lei, Yang Guodong. Geoid Refinement Based on Land Gravity and GPS/Leveling Data in Xingcheng Geophysical Survey Test Area[J]. Journal of Jilin University(Earth Science Edition), 2015, 45(2): 655-662.
地面重力数据结合GPS/水准数据精化兴城物探实验区大地水准面
吴琼1, 李树文1,2, 李宏卿1, 甄佳宁1, 李磊1,3, 杨国东1    
1. 吉林大学地球探测科学与技术学院, 长春 130026;
2. 济南市勘察测绘研究院, 济南 250013;
3. 中国电建集团昆明勘测设计研究院有限公司, 昆明 650051
收稿：2014-04-09
基金项目：国土资源部公益性行业科研专项项目(201011083)
作者简介: 吴琼(1972-),男,副教授,博士,主要从事大地测量学与测量工程方向研究,E-mail:Wuqiong@jlu.edu.cn
通讯作者:李树文（1990-），男，主要从事物理大地测量学与工程测量研究， Email:romanlsw@sina.com
摘要：区域大地水准面的确定是GPS测量常需解决的问题。目前确定大地水准面的方法主要包括重力法、GPS水准几何法及组合法,其中组合法因其精度和可靠性都较高,常用于计算高精度区域大地水准面。高精度的大地水准面模型是组合法确定区域大地水准面的关键。在我国,EGM2008全球重力场模型精度和分辨率均高于此前的所有模型,研究基于该模型的组合法大地水准面精化具有重要的实践意义。笔者以吉林大学兴城教学实习基地物探实验区为例,基于实测重力数据、EGM2008重力场模型和GPS水准数据,采用组合法精化了区域大地水准面,比较了组合法大地水准面模型和无重力实测数据的几何法大地水准面模型的精度差异,分析了该方法在物探测量中的适用性。结果表明,实验区组合法大地水准面模型精度最高达到1.2 cm,并且误差分布区间较小,总体上精度和可靠性高于对比的几何方法,并且组合法和几何法获取的两种大地水准面模型均能满足大比例尺物探测量要求。EGM2008模型精度较高,故平坦地区使用组合法时,高密度的实测重力数据可能带来高频扰动,有可能降低EGM2008重力场模型本身的精度,所以重力数据采集过程中要顾及重力点的密度和空间分布。本文方法更适用于地形复杂的地区。
关键词： EGM2008     组合法     大地水准面精化     物探测量    
Geoid Refinement Based on Land Gravity and GPS/Leveling Data in Xingcheng Geophysical Survey Test Area
Wu Qiong1, Li Shuwen1,2 , Li Hongqing1, Zhen Jianing1, Li Lei1,3, Yang Guodong1    
1. College of GeoExploration Science and Technology, Jilin University, Changchun 130026, China;
2. Ji'nan Institute of Survey and Investigation, Ji'nan 250013, China;
3. Kunming Engineering Corporation Limited, PowerChina, Kunming 650051, China
Abstract:The local geoid fluctuation is the major problem for the application of GPS survey. Algorithm for refining local geoid includes gravity method, GPS leveling method, and hybrid method. Hybrid method is widely applied due to its high precision and resolution, while high precision earth gravity model is the key for the hybrid method. The precision and resolution of EGM2008 earth gravity model is much higher than any gravity model in China. The study on its application for the refinement of local geoid has an important practical significance. We refined the geoid of the Xingcheng geophysical survey test area of Jilin University by means of hybrid method model (HMM), with using land gravity data, EGM2008, and GPS/leveling. The precision between the HMM and the model is refined by geometric method without comparision with the land gravity data(GMM). Both of the applicability of this method and EGM2008 are analyzed. The results indicate that the maximum precision of HMM in the test area is 1.2 cm with a minimum error distribution interval, and both of the precision and reliability of HMM are higher than the GMM in varied topography. High density gravity data in a much plane area may produce a high frequency disturb to EGM2008 because of its high precision, and this disturb may decrease the precision of EGM2008, which means that the spatial distribution of gravity data survey needs to be emphasized. The geoid refinement method reported in this article may be much more suitable for a complex topographic area.
Key words: EGM2008     hybrid method     geoid refinement     geophysical survey    

0 引言

物探测量是指在地球物理勘探作业中进行的各项测量工作的统称[1]，主要涉及平面测量和高程测量。大比例尺重力勘查等物探测量对物理点高程精度要求很高，例如，当布格重力异常设计总精度为0.025×10-5 m/s2时，要求物理点高程的均方根误差为0.05 m[2]。物探测量中常用的高程测量方法有：水准测量、三角高程测量和GPS(global position system)高程测量等。GPS高程测量具有测量速度快、全天候、精度高及不要求地面通视的特点[3]，在物探测量中应用广泛。GPS高程测量得到的是基于参考椭球面的大地高，需确定大地水准面差距来得到物理点高程。确定大地水准面差距的方法主要有：天文大地法、大地水准面模型法、重力测量法、几何内插法及残差模型法[4]。重力大地水准面与绝对大地水准面有一定的系统偏差；几何内插法适用于GPS水准点密度分布均匀的区域，未考虑大地水准面的起伏，在大地水准面起伏较大的山区准确度不高[4]。

为提高高程测量的精度和效率，物探测量中常采用局部大地水准面精化的方法来提高确定大地水准面差距的精度。局部大地水准面精化方法主要有重力移去恢复法、GPS水准几何法及组合法[5]，较高精度的全球重力场模型使得组合法确定大地水准面差距精度和可靠性都较高。采用GRACE(gravity recovery and climate experiment)卫星跟踪数据、卫星测高数据及地面重力数据计算得到的EGM2008重力场模型，其正常重力位及几何关系基于WGS-84参考椭球确定，球谐函数达2 159次且系数扩展到2 190阶[6]，模型高程异常在我国大陆的总体精度为20 cm，具有很好的适应性[7]。

笔者采用组合法精化测区局部大地水准面，先利用“移去-计算-恢复”法确定重力大地水准面[8]；再以GPS水准点作为控制点，利用几何法精化重力大地水准面。精化后的大地水准面既有几何法大地水准面模型的高精度又有重力大地水准面模型的高分辨率。 1 研究方法

利用组合法精化局部大地水准面时，首先，将实测重力值归算至大地水准面；其次，确定重力大地水准面，即“移去-计算-恢复”过程[9]。“移去”：将均匀格网点空间重力异常“观测值”移去EGM2008重力异常模型分量，得到残差重力异常分量；“计算”：利用stokes公式计算得到大地水准面差距残差分量；“恢复”：将EGM2008大地水准面模型分量和地形对大地水准面差距的间接影响分量恢复，确定每个点的重力大地水准面差距。最后，利用几何法精化重力大地水准面模型[10, 11, 12]。测区范围较小，大地水准面差距和高程异常互差变化很小，文中对大地水准面差距和高程异常不再区分。笔者将组合法得到的大地水准面模型[13](hybrid method model，HMM)与无重力测量数据几何法精化得到的大地水准面模型(geometric method model，GMM)进行比较，并分析二者精度和可靠性的差异。 1.1 重力数据预处理

“移去-计算-恢复”法确定重力大地水准面模型时，需采用stokes公式计算大地水准面残余分量。利用stokes公式计算的前提是大地水准面外部没有质量且实测重力归算至大地水准面上[14]。因地形均衡异常更为光滑，获取该异常前实测重力需进行空间改正、层间改正、局部地形改正及地形均衡改正(表 1)。局部地形改正和地形均衡改正采用SRTM(shuttle radar topography mission)数据。

表 1 重力改正及地形均衡重力异常计算公式[14, 15, 16, 17] Table 1 Formulas of gravity corrections and the terrain isostatic gravity anomalies[14, 15, 16, 17]
重力改正和计算公式公式中符号意义
空间改正
δg1=0.308 6hP-0.72×10-7Ph2 ρ0为地壳平均密度，取2.6 g/cm3，Δρ1为补偿密度[18]，取0.6g/cm3
层间改正G为万有引力常数
δg2=-0.041 8ρ0hPhP,h分别为计算点P(xP,yP)和流动点(x,y)的高程
局部地形改正dσ=dxdy，其中(x,y)为平面坐标，σ为计算点周围的球冠，其半径小于100 km可视为平面
δgTC=Gρ0∭hhP z-hPl3 dzdσD为岩浆面深度，取32 km
地形均衡改正d(x,y)为山根深度[18]，d(x,y)=4.45h(x,y)
δgIC=GΔρ1∭D+d(x,y)D z-hPl3 dzdσl为计算点与流动点之间的距离，l=[(x-xP)2+(y-yP)2+(z-zP)2]1/2
地形均衡重力异常g为计算点的实测地面绝对重力值
ΔgIC=g+δg1+δg2+δgTC+δgIC-γ0γ0为正常重力值γ0=9.780 3268×[1+0.005 302 4sin2(φ)-0.000 005 8sin2(2φ)]
表选项

重力归算得到大地水准面上离散点的地形均衡异常“观测值”。以R1为半径将拟合区划分为两个环带，采用改进的Shepard插值模型方法获得EGM2008重力场模型对应均匀格网点处的“观测值”。定义权函数[17] p(l)：

对应的插值函数[17]为
式中：(φ,λ)为计算点的纬度值和经度值；内插计算点数N≤10；l为已知点与计算点的距离；f为参与计算已知点的地形均衡重力异常。内插得到均匀格网点处地形均衡重力异常值ΔgIi，恢复得到每个均匀格网点处自由空间重力异常的“观测值”：
1.2 “移去-计算-恢复”法确定重力大地水准面

利用重力场的“可叠加性”原理[14]，将重力大地水准面模型Ng分为3个分量：Ng=NGM+δNT+δNr，NGM是模型大地水准面差距，δNT是局部地形对大地水准面的间接影响，δNr是大地水准面残余分量。相应地，重力异常Δg也分为3个分量：Δg=ΔgGM+δΔgT+δΔgr，ΔgGM是EGM2008重力场模型确定的模型自由空间重力异常，δΔgT是由地形引起的地形重力效应，δΔgr是残差重力异常。 1.2.1 “移去”

将实测重力异常移去EGM2008重力场模型分量和地形重力效应，得到重力异常残差分量：

δΔgr=Δg-ΔgGM-δΔgT 。

EGM2008重力场模型计算地面点的自由空间重力异常的公式[6, 7, 14]为
式中：GM为地心引力常数(M为地球总质量)； R为地球平均半径；θ为极距；Cnm,Snm为完全规格化位系数； nm(sinθ)为完全规格化缔合勒让德函数；Pnmax=2 159。地形重力效应与局部地形改正的计算公式相同，均匀格网点处的重力异常残差分量为

δΔgri=ΔgFi-ΔgGMi 。

1.2.2 “计算”

stokes公式球坐标积分形式[14]为NP= R 4πγ [Δg(φ,λ)

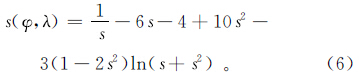
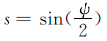式中：(φ,λ)为球面流动点的球面纬度及球面经度；s(φ,λ)为斯托克斯核函数。
式中,(ψ 2 ),ψ为计算点P(φP,λP)与球面流动点(φ,λ)之间的球面角距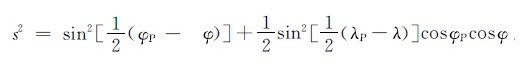；。由公式(6)可得到计算点的残差大地水准面分量[19]。笔者采用“改进的Shepard插值模型”建立大地水准面差距残差模型。 1.2.3 “恢复”

EGM2008重力场模型计算大地水准面差距的公式[6, 14]为

式中，r为矢径。

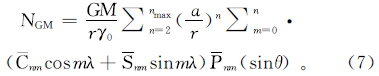
局部地形对大地水准面差距的间接影响为调整后的大地水准面与实际大地水准面之间的距离，计算公式[14 ,20]为

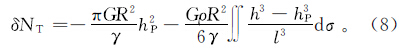
式中：l为计算点与流动点之间的距离，在球面坐标系中用角距表示；hP和h分别为计算点和流动点的高程，本文计算时取到2次项。

得到计算点的重力大地水准面差距为

1.3 GPS水准几何法精化重力大地水准面

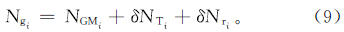
利用GPS水准点精化重力大地水准面模型也是一个“移去-计算-恢复”的过程。计算控制点处实测大地水准面差距与重力大地水准面差距的差值δNi=NCi-Ngi。笔者采用了二次曲面拟合(QSF)、反距离加权(IDW)、移动曲线(MC)、三次样条插值(CS)、最小二乘配置(Lsc)5种方法建立残差大地水准面模型δN(x,y)[21],恢复重力大地水准面分量得到各点精化后的大地水准面差距[22, 23]：

N(xi,yi)=Ngi+δN(xi,yi) 。

2 研究区概况

吉林大学兴城物探实验区位于辽宁省兴城市西北部，海拔最大落差约450 m，主要服务于地质仪器标定[24]，还可用于吉林大学测量、地质、物探等专业教学实习。实验区GPS控制网按D级网要求布设、C级网要求观测[25]。布设静态GPS控制点12个，长时间联测IGS跟踪站(观测时长72 h)以获取控制网基准；二等水准测量[26]联测GPS点(4个静态GPS水准点，23个RTK(real-time kinematic)水准点，RTK点与基准站距离小于10 km)，水准路线长度约130 km，东南起点联测一等水准点1个，水准路线每隔约15 km实测重力值以求定水准测量的重力异常改正[26]，测量精度如表 2所示。重力测量选择实验区内长70 km、宽20 km的区域，按3 km平均点距实测重力点108个，联测秦皇岛国家重力基点。按3 km平均点距选取GPS水准点作为控制点(17个)参与模型计算，剩余点(10个)作为检查点(图 1)。

表 2 测量精度统计 Table 2 Statistics of measurement accuracy
内容统计项精度
GPS测量静态测量预处理复测基线的长度差/mm≤17
最简异步环全长闭合差/mm≤72
无约束平差中基线向量改正数的绝对值/mm≤14
约束平差后，约束点间的边长相对中误差≤1/163 983
最弱基线相对中误差≤1/172 711 6
动态测量统计项纬度/(″)经度/(″)大地高/m
检查点互差最大值0.014 40.027 10.009
检查点互差最小值0.009 70.003 40.004
检查点互差平均值0.011 40.004 50.004
水准测量每测段往返测量闭合差最大值/mm3.65
每测段往返测量闭合差均值/mm2.51
每测段往返测量闭合差最小值/mm0.07
重力测量检查点处测量较差/ mGal0.058 3
表选项
图 1 研究区及点位分布

 Fig. 1 Map of study area and the distribution of points
图选项
3 结果

各方法在控制点处的计算误差[22]见表 3(计算误差为0的方法点未列出)。比较不同的拟合方法可知，QSF-GMM均方根误差最大，达3.2 cm。建立最小二乘配置法对应的水准面模型时，分别采用了二次曲面拟合(LscS)和二次曲线拟合(LscL)两种方法。二次曲面最小二乘配置法得到的组合法大地水准面模型 (LscS-HMM)均方根误差最小，为0.8 cm，误差最大值的绝对值最小，为1.0 cm，误差区间最小，为2.8 cm。QSF-GMM对应的误差区间最大，为10.9 cm；二次曲线最小二乘配置法得到的组合法大地水准面模型(LscL-HMM)对应误差最小值的绝对值最小，为1.7 cm。QSF-GMM对应误差最大值和最小值的绝对值最大，分别达4.6 cm和6.3 cm。

表 3 控制点计算误差 Table 3 Error statistics of control points
cm
最大值最小值最大值与

最小值之差		平均值均方根

误差
QSFGMM4.6-6.310.90.03.2
HMM3.5-2.35.8-0.41.6
LscSGMM2.6-2.85.40.01.5
HMM1.0-1.82.80.10.8
LscLGMM2.8-3.56.30.01.6
HMM2.4-1.74.1-0.11.1
表选项

QSF-GMM均方根误差和误差区间均约为QSF-HMM的2倍，误差最大值和最小值的绝对值均大于QSF-HMM；采用LscS拟合残差模型时，GMM的均方根误差和误差区间均接近HMM的二倍；采用LscL拟合模型时，GMM的均方根误差、误差区间及最大值及最小值的绝对值都比HMM高。

各方法在检查点处的计算误差[22]见表 4。IDW-GMM均方根误差最大，达3.7 cm，QSF-HMM均方根误差最小，为1.2 cm；IDW-GMM对应的误差区间最大，为7.4 cm，QSF-HMM对应的误差区间最小，为2.7 cm；IDW、MC误差平均值的绝对值最小，为0.2 cm，QSF-GMM对应误差平均值的绝对值最大，达1.9 cm。

表 4 检查点计算误差 Table 4 Error statistics of check points
cm
最大值最小值最大值与

最小值之差		平均值均方根

误差
QSFGMM2.4-1.43.81.93.5
HMM1.2-1.52.7-1.31.2
IDWGMM3.4-4.07.4-0.23.7
HMM1.4-3.04.4-0.21.8
MCGMM2.1-2.74.8-0.22.4
HMM2.3-3.55.80.22.4
CSGMM2.1-2.64.70.52.3
HMM1.4-2.64.0-0.71.6
LscSGMM2.0-1.13.10.31.6
HMM1.0-2.53.4-1.01.4
LscLGMM2.3-0.93.20.51.6
HMM0.9-2.53.4-0.91.4
表选项

采用QSF时，GMM均方根误差为3.5 cm，约是HMM的3倍，误差区间、误差平均值均大于HMM；采用MC拟合残差模型时，GMM的均方根误差与HMM的相等，误值平均值和误差区间均接近HMM；采用CS拟合模型时，GMM的均方根误差和误差区间均比HMM大；采用LscS拟合残差模型时，GMM的均方根误差比HMM的稍大，误差平均值GMM的绝对值小于HMM；采用LscL拟合模型时，GMM的均方根误差比HMM的稍大，误差平均值的绝对值GMM小于HMM。

在控制点内部：HMM的精度均高于GMM；HMM的误差区间、差值最大值和最小值的绝对值均小于GMM。在检查点处：除MC法对应的两个模型精度相等以外，HMM均高于GMM；HMM与GMM对应的误值平均值的绝对值相差不大，QSF法、IDW法、CS法对应的GMM的误差区间比HMM对应的误差区间大，MC法、LscL法和LscS法对应的GMM的误差区间比HMM对应的误差区间小。综上所述，GMM和HMM在控制点和检查点处均能达到厘米级精度，HMM的内部可靠性大于GMM，外部可靠性方面，HMM与GMM基本一致。

4 结论和讨论

笔者在兴城物探实验区基于重力观测数据、EGM2008重力场模型及GPS水准数据，采用组合法精化物探测区大地水准面，计算后发现组合法大地水准面模型和几何法大地水准面模型均能满足大比例尺物探测量的精度要求。因地面重力数据可考虑到大地水准面的起伏[23]，组合法得到的局部大地水准面模型的精度与可靠性均较高。采用组合法精化大地水准面，选择拟合方法也很重要，组合法模型中均方根误差最大与最低相差1倍。

组合法水准面模型与几何法水准面模型相比，可靠性和精度均高，大比例尺重力勘查时，获取实测重力数据成本低，使得组合法精化大地水准面在物探测量中更可行。

组合法得到的高精度大地水准面不仅为物探测量,也可为测绘学、地球动力学、地质学等相关学科的发展和应用提供重要的基础地球空间信息[11, 27, 28]。基于EGM2008重力场模型得到的组合法模型与基于CQG2000似大地水准面得到的组合法模型相比，在相同的GPS水准和重力数据情况下，其精度和可靠性都可能会更高。平坦地区使用EGM2008重力场模型组合法时，高密度的实测重力数据也可能带来高频扰动，有可能降低其EGM2008重力场模型本身的精度，所以重力数据采集过程中要顾及重力点的密度和空间分布。采用实测重力数据和高精度重力场模型的组合法更适用于地形复杂的地区。

参考文献
[1] SY/T5171-2011陆上石油物探测量规范[S].北京:石油工业出版社, 2011. SY/T5171-2011 Specifications of Survey for Petroleum Geophysical Prospecting on Land[S].Beijing:Petroleum Industry Press, 2011.
[2] DZT 0171-1997 大比例尺重力勘查规范[S].北京:中国标准出版社, 1997. DZT 0171-1997 Specifications of Large Scale Gravitational Perambulation[S].Beijing:China Standard Press, 1997.
[3] 张正禄, 邓勇, 罗长林, 等. 利用GPS精化区域似大地水准面[J].大地测量与地球动力学, 2006, 26(4):14-17. Zhang Zhenglu, Deng Yong, Luo Changlin, et al. Refining Local Quasi Geoid with GPS[J].Journal of Geodesy and Geodynamics, 2006, 26(4):14-17.
[4] 李征航, 黄劲松.GPS测量与数据处理[M]. 武汉:武汉大学出版社, 2005. Li Zhenghang, Huang Jinsong. GPS Surveying and Data Processing[M].Wuhan:Wuhan University Press, 2005.
[5] 马新莹, 何志堂, 于丹, 等. 不同大地水准面精化方法的试算与分析[J].测绘技术装备, 2009, 11(1):9-12. Ma Xinying, He Zhitang, Yu Dan, et al. Calculation and Analysis of Different Methods for Refine Geoid Model[J].Geomatics Technology and Equipment, 2009, 11(1):9-12.
[6] Pavlis N K, Holmes S A, Kenyon S C, et al.An Earth Gravitational Model to Degree 2160:EGM2008[C]//2008 General Assembly of the European Geosciences Union. Vienna:Apill, 2008.
[7] 章传银, 郭春喜, 陈俊勇, 等. EGM2008地球重力场模型在中国大陆适用性分析[J].测绘学报, 2009, 38(4):283-289. Zhang Chuanyin, Guo Chunxi, Chen Junyong, et al. EGM2008 and Its Application Analysis in Chinese Mainland[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(4):283-289.
[8] GBT 23709-2009区域似大地水准面精化基本技术规定[S]. 北京:中国标准出版社, 2009. GBT 23709-2009 Basic Specifications for Region Quasi-Geoid Determination[S]. Beijing:China Standard Press, 2009.
[9] Bae T S, Lee J, Kwon J H, et al. Update of the Precision Geoid Determination in Korea[J].Geophysical Prospecting, 2012, 60:555-571.
[10] Tóth G Y, Sžucs E. On the Determination of a New Combined EGM2008 Based Quasi-Geoid for Hungary[J].Acta Geodaetica et Geophysica Hungarica, 2011, 46(4):417-430.
[11] 宁津生, 罗志才, 李建成.我国省市级大地水准面精化的现状及技术模式[J].大地测量与地球动力学, 2004, 24(1):4-8. Ning Jinsheng, Luo Zhicai, Li Jiancheng. Present Situations and Technical Modes for Refining Provincial(Municipal) Geoid in China[J]. Journal of Geodesy and Geodynamics, 2004, 24(1):4-8.
[12] 宁津生, 罗志才, 杨沾吉, 等.深圳市1 km高分辨率厘米级高精度大地水准面的确定[J].测绘学报, 2003, 32(2):102-107. Ning Jinsheng, Luo Zhicai, Yang Zhanji, et al. Determination of Shenzhen Geoid with 1 km Resolution and Centimeter Accuracy[J].Acta Geodaetica et Cartographica Sinca, 2003, 32(2):102-107.
[13] Hirt C, Featherstone W E, Marti U. Combining EGM2008 and SRTM/DTM2006.0 Residual Terrain Model Data to Improve Quasi-Geoid Computations in Mountainous Areas Devoid of Gravity Data[J].Journal of Geodesy, 2010, 84(9):557-567.
[14] Chen Yongqi, Luo Zhicai. A Hybrid Method to Determine a Local Geoid Model-Case Study[J].Earth Planets Space, 2004, 56:419-427.
[15] 海斯卡涅W A, 莫里斯H.物理大地测量学[M]. 卢福康, 胡国理, 译.北京:测绘出版社, 1967. Heiskanen W A, Moritz H. Physical Geoolesy[M]. Translated by Lu Fukang, Hu Guoli. Beijing:Surveying and Mapping Press, 1967.
[16] 管泽霖, 宁津生. 地球形状及外部重力场:上册[M]. 北京:测绘出版社, 1981. Guan Zelin, Ning Jinsheng. The Shape of the Earth and Its External Gravity Field:The First Volume[M].Beijing:Surveying and Mapping Press, 1981.
[17] 李建成, 陈俊勇, 宁津生, 等.地球重力场逼近理论与中国 2000 似大地水准面的确定[M]. 武汉:武汉大学出版社, 2003. Li Jiancheng, Chen Junyong, Ning Jinsheng, et al. The Theory of Approaching Earth Gravity Field and Evaluation of Chinese 2000 Qusi-Geoid[M]. Wuhan:Wuhan University Press, 2003.
[18] 李建成, 畅毅, 董兰生, 等.陕甘宁盆地大地水准面精化问题研究[J].物探装备, 1999, 9(4):6-12. LI Jiancheng, Chang Yi, Dong Lansheng, et al. Optimized Geoid Determination in Shan-Gan-Ning Basin[J]. Equipment for Geophysical Prospecting, 1999, 9(4):6-12.
[19] 李建成.最新中国陆地数字高程基准模型:重力似大地水准面 CNGG2011[J].测绘学报, 2012, 41(5):651-660, 699. Li Jiancheng. The Recent Chinese Terrestrial Digital Height Datum Model:Gravimetric Quasi-Geoid CNGG2011[J].Acta Geodaetica et Cartographica Sinica, 2012, 41(5):651-660, 699.
[20] 晁定波.关于 Stokes 公式的球面卷积和平面卷积的注记[J].武汉大学学报:信息科学版, 2004, 28(6):651-654. Chao Dingbo. A Note on Stokes Formula in the Form of Spherical and Planar Convolution[J]. Geomatics and Information Science of Wuhan University, 2004, 28(6):651-654.
[21] 李树文, 吴琼, 李宏卿, 等.EGM2008重力场模型在兴城物探测量中的应用[J].世界地质2014, 33(1):209-214. Li Shuwen, Wu Qiong, Li Hongqing, et al. An Application of EGM2008 for Geophysical Prospecting Survey in Xingcheng[J].Global Geology, 2014, 33(1):209-214.
[22] 郭东美, 许厚泽.应用GPS水准与重力数据联合解算大地水准面[J].武汉大学学报:信息科学版, 2011, 36(5):621-624. Guo Dongmei, Xu Houze. Determination of Geoid Using GPS Leveling and Gravity Data[J]. Geomatics and Information Science of Wuhan University, 2011, 36(5):621-624.
[23] Prutkin I, Klees R. On the Non-Uniqueness of Local Quasi-Geoids Computed from Terrestrial Gravity Anomalies[J].Journal of Geodesy, 2008, 82(3):147-156.
[24] 黄大年, 于平, 底青云, 等.地球深部探测关键技术装备研发现状及趋势[J].吉林大学学报:地球科学版, 2012, 42(5):1485-1496. Huang Danian, Yu Ping, Di Qingyun, et al. Development of Key Instruments and Technologies of Deep Exploration Today and Tomorrow[J]. Journal of Jilin University: Earth Science Edition, 2012, 42(5):1485-1496.
[25] GB/T18314-2009 全球定位系统(GPS)测量规范[S].北京:中国标准出版社, 2009. GB/T18314-2009 Specifications for Global Position System (GPS) Surveys[S]. Beijing:China Standard Press, 2009.
[26] GB/T12897-2006国家一、二等水准测量规范[S].北京:中国标准出版社, 2006. GB/T12897-2006 Specifications for the First and Second Order Leveling[S]. Beijing:China Standard Press, 2006.
[27] Marti U.Comparison of High Precision Geoid Models in Switzerland[M]//Jekeli C. Gravity, Geoid and Space Missions.:Springer, 2004:377-382.
[28] Featherstone W E. On the Use of the Geoid in Geophysics:A Case Study Over the North-West Shelf of Australia[J]. Exploration Geophysics, 1997, 28(1):52-57.
http://dx.doi.org/10.13278/j.cnki.jjuese.201502307
吉林大学主办、教育部主管的以地学为特色的综合性学术期刊
0

文章信息

吴琼, 李树文, 李宏卿, 甄佳宁, 李磊, 杨国东
Wu Qiong, Li Shuwen, Li Hongqing, Zhen Jianing, Li Lei, Yang Guodong
地面重力数据结合GPS/水准数据精化兴城物探实验区大地水准面
Geoid Refinement Based on Land Gravity and GPS/Leveling Data in Xingcheng Geophysical Survey Test Area
吉林大学学报(地球科学版), 2015, 45(2): 655-662
Journal of Jilin University(Earth Science Edition), 2015, 45(2): 655-662.
http://dx.doi.org/10.13278/j.cnki.jjuese.201502307

文章历史

收稿: 2014-04-09

相关文章

工作空间