0 前言
近年来全球气候问题逐渐加剧,政府间气候变化专门委员会(IPCC)的系列研究指出温室气体(尤其是CO2气体)的大量排放是主要影响因素之一[1, 2],该结论已经得到了世界范围科学研究者的认可,因此CO2减排已迫在眉睫。深部咸水层由于其分布广、经济价值小和储存潜力巨大而被公认为是进行规模化CO2地质储存最有潜力的场所[1, 3]。
注入大量CO2到咸水层中涉及到复杂的热-水动力-力学耦合过程,而该过程的刻画是预测CO2的迁移转化规律、评价储存能力和分析其泄漏风险的关键。热-水动力-力学过程之间的互相耦合是异常复杂的,实验只能研究其中的部分耦合过程,而数值模拟能够充分考虑它们之间的互相耦合过程。在CO2地质储存的耦合数值模拟中,研究最多的是水动力和力学之间的耦合,对应地使用最多的模拟工具是TOUGH2-FLAC3D[4]。该软件由Rutqvist于2002年通过耦合热-水动力(TH)软件TOUGH2和力学分析软件FLAC3D形成,并成功应用于深部咸水层注入CO2后CO2运移和压力上升[4]、盖层力学变化[5]、最大CO2持续注入压力[6]和Salah场地CO2注入后的地表位移分析[7]。最近TOUGHREACT和FLAC3D被联合在一起用于研究CO2注入后的热-水动力-力学和化学耦合过程[8, 9]。Winterfeld等[10]在TOUGH2的基础上开发了并行的热-水动力和力学模拟器。Hu等[11]基于平均应力法耦合TOUGH2建立了热-水动力-力学模拟器TOUGH2-EGS,并应用到干热岩中。
虽然TOUGH2-FLAC3D能够很好地模拟CO2地质储存过程的热-水动力-力学(THM)耦合过程,然而两个独立的代码使得其间的耦合是松散的,计算效率较低;同时FLAC3D代码的封闭模式使得对力学模型刻画的理解和改进几乎不可能。笔者首先基于Terzaghi固结理论和TOUGH2的热-水动力耦合模型,建立了热-水动力-力学耦合模型;然后在TOUGH2代码的基础上,开发了力学模块形成了新的热-水动力-力学模拟器,并通过与解析解对比验证了其正确性;最后通过改进的程序研究了鄂尔多斯盆地深部咸水层二氧化碳地质储存过程中的热、水动力和力学变化过程。
1 THM模拟器和验证
1.1 THM过程数学模型
地下多孔介质中的流体(包括地层水和CO2)流动一般符合达西定律,热流包括对流和传导两部分。基于质量和能量守恒,可建立多相流动和热对流传导方程[12]:

流动过程为

热对流传导为

而在力学模型的建立过程中,由于地表是位移自由面,加之地层具侧向无限延伸性,可以假设CO2注入过程中引起的垂直总应力不变[6],地层变形侧向受限,只在垂直方向上下变形。由此得到有效应力变化和垂向应变方程。
有效应力变化为

平均有效应力变化为
垂向应变为

TOUGH2系列[12]是国际上先进的TH耦合过程数值模拟程序,其能够刻画多个过程和可信的模拟结果[13],因此被广泛用于CO2地质储存的研究中[5, 14, 15, 16]。ECO2N[17]是TOUGH2的一个模块,能够刻画H2O、CO2和NaCl系统中的多相流动和热对流传导过程。为了充分利用它的优势,本文的力学模型直接被嵌入到该程序中。继承TOUGH2的时空离散特征,本文改进的THM模拟器(THM-Terzaghi)采用隐式时间差分和空间任意形状的积分有限差。
1.2 THM过程耦合方法
通常情况下,THM过程耦合方法可以分为两类:全耦合和部分耦合。采用全耦合方法可以得到准确的结果,但将花费大量的计算机时间,而部分耦合虽然结果精度上有所降低,但是算法实现相对容易。TOUGH2中TH的耦合采用的是全耦合法,而添加的力学采用的是部分耦合法,即在计算完温度和压力后直接利用力学模型计算有效应力变化和应变,并根据有效应力的变化修改孔隙度和渗透率[4, 5]:

1.3 THM模拟器验证
为了验证开发的THM-Terzaghi程序的正确性,笔者通过与两个存在解析解问题的对比进行了验证。一维固结沉降问题(图 1,表 1)的对比结果(图 2)显示,THM-Terzaghi程序的计算结果和解析解差别不大,从而证明了THM-Terzaghi在水动力-力学(HM)耦合方面具可靠性;一维温度传导问题(图 3,表 2)的对比结果(图 4)显示,THM-Terzaghi在温度-力学(TM)耦合方面具可靠性。
 |
| 图 1 一维固结沉降概念模型Fig. 1 Conceptual model of 1D settlement induced by consolidation |
| 参数 | 取值 |
| 厚度/m | 50 |
| 渗透率/m2 | 1.0×10-14 |
| 黏度/(kg/(m·s)) | 8.9×10-3 |
| 体积模量/Pa | 8×107 |
| 泊松比 | 0.20 |
| Biot系数 | 1.0 |
| 荷载/(105 Pa) | 3.0 |
 |
| 图 2 一维固结沉降解析解和THM-Terzaghi数值解结果对比Fig. 2 Comparison of analytical and numerical solutions for 1D settlement induced by consolidation |
| 参数 | 取值 |
| 厚度/m | 50 |
| 渗透率/m2 | 0.0 |
| 密度/(kg·m-3) | 2 550 |
| 孔隙度 | 0.01 |
| 热传导系数/(W/(m·℃)) | 2.34 |
| 热膨胀系数/K-1 | 1.5×10-6 |
| 比热容/(J/(kg·℃)) | 690 |
| 泊松比 | 0.20 |
| 初始温度/℃ | 60 |
| 边界温度/℃ | 10 |
对于上面的一维固结沉降问题,可以得到超孔隙水压力分布和沉降的解析解[18]。
超孔隙水压力为

地表位移为

 |
| 图 3 一维热传导引起的沉降概念模型Fig. 3 Conceptual model of 1D settlement induced by thermal conduction |
 |
| 图 4 一维温度传导引起沉降解析解和THM-Terzaghi数值解结果对比Fig. 4 Comparison of analytical and numerical solutions for 1D settlement induced by thermal conduction |
对于上面的一维热传导引起的沉降问题,可以得到温度分布和沉降的解析解[19]。
温度为

地表位移为
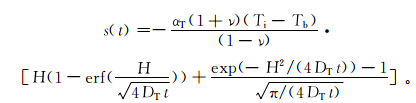
 ,η为积分变量;DT为热扩散系数,
,η为积分变量;DT为热扩散系数, 。
。2 模型建立
2.1 鄂尔多斯CCS示范工程简介
鄂尔多斯盆地是我国陆上第二大沉积盆地,盆地面积约为24万 km2,形成于晚三叠世。盆地内含有丰富的石油、煤炭、天然气和煤层气等资源,是我国重要的能源基地。区内存在或即将建成多个煤炭转化等能源基地,包括煤制油、煤制甲醇、煤制烯烃和煤制天然气等项目,这些煤化工项目建成后将形成大量的CO2集中排放源。目前已投产的煤化工项目每年排放CO2约870 万t;据初步估计,在建项目全部投产后将每年排放CO2近5 400 万t[20]。如此多的CO2排放将是制约当地煤化工项目的瓶颈之一。
为应对全球气候变化,实现CO2减排,神华集团2002年以来陆续开展了一系列CO2捕获和储存(CCS)的研究工作,并于2010年开始正式实施中国第一个CCS示范工程建设,2011年1月试注成功,2013年4月累计注入10 万t。
注入场地位于伊金霍洛旗,离神华煤制油公司直线距离约为12 km。注入井深约2 500 m,依次穿过第四系,白垩系志丹群,侏罗系安定组、直罗组和延安组,三叠系延长组、纸坊组、和尚沟组和刘家沟组,以及二叠系石千峰组、石盒子组、山西组,石炭系太原组、本溪组和奥陶系马家沟组。整套地层中存在多套适于CO2地质储存的储盖层组合,其中石千峰和刘家沟储盖层组合被认为是储层条件最好和最具有潜力的层位[21]。
注入井共射孔18层,累计厚度为88 m,其中石千峰组为52 m,占60%。在离注入井50 m和80 m处各有一口监测井,用于监测压力、温度和CO2气体饱和度等。采用多层单井混合方式注入,分层监测。
2.2 概念模型
根据场地岩石的岩石矿物分析,储层以含长石类的砂岩为主,砂岩中石英和长石体积分数最大分别可占到50%和40%。矿物捕集过程中反应缓慢,在百年的时间尺度内,对CO2的矿物捕获几乎没有贡献。因此,在本文模型建立中忽略化学反应过程,仅仅考虑了温度、压力和力学之间的耦合过程。
石千峰和刘家沟储盖层组合(图 5)是本区CO2地质储存最有潜力的层位,根据测井数据,初步估计其可容纳注入CO2的一半左右。为了简化模型,笔者以该套组合为研究对象,分析CO2注入到地层后的温度场、压力场、位移和有效应力,以及CO2晕运移的时空演化过程。
 |
| 图 5 石千峰和刘家沟储盖层组合地层特征描述Fig. 5 Description of Shiqianfeng-Liujiagou storage-caprock formations |
石千峰和刘家沟储盖层可用的储层共有8层,累计厚度为51.8 m,单层的最大厚度为9.0 m,最小为4.4 m。砂岩储层的渗透率在10-15 m2数量级上,而泥岩的在10-17 m2数量级上;砂岩的孔隙度约为0.10,泥岩的约为0.03(图 5)。根据这些特征可知,石千峰储层是低孔低渗的薄砂层储层,刘家沟的超低渗泥岩是理想盖层。
鄂尔多斯深部地层倾斜度为1°~3°,接近水平。对于水平分布的地层,THM模型可以采用以注入井为中心的径向模型(图 6)来大大缩减模型中网格的数目。模型垂向上为考虑盖层的影响,上下范围分别扩展到泥岩中,最终埋深为1 576~2 160 m,由于泥岩的阻隔作用设定其为隔水边界;水平方向上取10 km位置给一类定压力边界条件。在CO2注入过程中,温度的对流传导较慢,影响范围远远小于压力的影响范围,因此,上下边界采用隔热,侧向边界温度恒定(实际上采用隔热并不影响计算结果)。初始温度根据Ti=10.5+0.031 9d(d为埋深)确定,初始压力服从静水压力,初始垂向应力假设仅仅是由于上覆地层的自重引起,初始水平应力满足侧向受限的静止应力状态。
 |
| 图 6 CO2注入二维径向概念模型Fig. 6 2D radial conceptual model for CO2 injection into aquifers |
为了最大限度地利用储层的空间,在注入前CO2被压缩到超临界状态(为了简化,本文称为气相) (P>7.382 MPa,T>31.04 ℃)。井筒中的流体流动速度很快,远远大于其在储层中的流动;而相对孔隙介质,井筒要光滑得多,因此,可以假设流体在其中的流动能量损失忽略。那么,井筒中的压力仅受重力影响,其满足方程Pn+1=Pn+ρngΔz(Pn为井筒中第n个网格中的压力;ρn为第n个网格的CO2密度;Δz为第n个网格的垂向长度。Pn+1是第n个网格压力和密度的函数)。由于CO2的可压缩性,其密度在井筒中并不恒定,是温度和压力的函数,需要采用“由上至下”的计算方法得到与储层相连位置处的注入压力。根据实际注入情况,井口注入温度和压力分别为35.0 ℃和8.0 MPa。 2.3 模型参数
地层基本参数见表 3,相对渗透率和毛细压力均采用Van Genuchten模型,泥岩的毛细进入压力比砂岩大两个数量级。
在考虑力学的耦合效应时,最为关键的参数是耦合方程中的实验参数a和c,这两项根据前人[4, 5]总结分别取5×10-8 Pa-1和22.2。为了使平均有效应力、孔隙度,以及渗透率在初始状态保持一致,需要得到每一个位置的残余和零应力状态的孔隙度,以及零应力状态下的渗透率。假设孔隙度变化为实际孔隙度的10%,即φ0-φr=0.1φ。由于砂岩 储层均为薄砂层,有效应力在每一层中变化不大,因此,可以简化为计算每一储层的残余和零应力状态的孔隙度,以及零应力状态下的渗透率,计算结果见表 4,其中忽略泥岩孔渗变化。
| 主要参数 | 参数取值 | 其他参数 | 参数取值 | |
| 岩石密度/(kg/m3) | 2 260 | 相对渗透率模型 | 液相(Van Genuchten) | |
| 岩石热传导系数/(W/(m·℃)) | 2.51 | S1r | 0.30 | |
| 岩石比热/(J/(kg ·℃)) | 920 | m | 0.457 | |
| 岩石热膨胀系数/(1/℃) | 10-6 | 气相 (Corey): | ||
| 盐度/% | 2 | Sgr | 0.05 | |
| 砂岩体积模量/GPa | 10.0 | 毛细压力模型 | Slr | 0.00 |
| 泥岩体积模量/GPa | 5.0 | (Van Genuchten): | P0/kPa | 砂岩为19.6,泥岩为3100.0 |
| 泊松比 | 0.25 | m | 0.457 | |
| 注: Slr. 残余水饱和度; Sgr. 残余气饱和度; m.经验指数; P0. 毛细进入压力。液相相对渗透率模型:krl= S* {1-(1-[S*]1/m)m}2;气相相对渗透率模型:krg=(1- )2(1- 2);毛细压力模型:Pcap=-P0([S*]-1/m-1)1-m。其中,S*=(S1-Slr)/(1-Slr); =(S1-Slr)/(S1-Slr-Sgr);krl. 液相相对渗透率;krg. 气相相对渗透率;Pcap. 毛细压力。 | ||||
| 储层编号 | 厚度/m | 孔隙度 | 渗透率/(10-15m2) | |||
| 零应力状态 | 残余 | 实际 | 零应力状态 | 实际 | ||
| R1 | 9.0 | 0.105 | 0.095 | 0.10 | 7.36 | 2.80 |
| R2 | 5.4 | 0.126 | 0.113 | 0.12 | 15.40 | 5.70 |
| R3 | 5.6 | 0.105 | 0.095 | 0.10 | 4.52 | 1.60 |
| R4 | 7.6 | 0.052 | 0.047 | 0.05 | 0.28 | 0.10 |
| R5 | 5.4 | 0.105 | 0.095 | 0.10 | 5.18 | 1.80 |
| R6 | 4.4 | 0.105 | 0.095 | 0.10 | 6.94 | 2.40 |
| R7 | 7.2 | 0.116 | 0.104 | 0.11 | 10.20 | 3.50 |
| R8 | 7.2 | 0.137 | 0.123 | 0.13 | 19.60 | 6.60 |
| 泥岩 | 467.9 | 0.030 | 0.030 | 0.03 | 0.08 | 0.08 |
对于2D的径向模型,网格由以注入井为中心的一系列圆环组成。单元在水平方向上共有101个,垂向上共有85个,合计8 585个。水平方向上网格大小由近井的0.2 m逐渐对数增长到边界的800.0 m。垂向上为了刻画CO2的重力翻转现象,储层及附近进行了网格加密,最小网格大小为2.4 m,最大为泥岩中的10.0 m(图 7)。
 |
| 图 7 二维径向网格剖分Fig. 7 Grid generation for 2D radial model |
3.1 温度时空变化特征
相对冷的CO2注入到咸水层后将导致地层温度的降低。砂岩储层中热以对流和传导两种形式进行传递,而上下相邻的泥岩中热主要以传导为主,故导致温度主要沿着咸水层变化。注入1 a后,CO2注入引起的温度变化在侧向上的最大距离约为29 m,20 a后约为74 m(图 8)。在垂向上,注入20 a后部分层位的温度变化已经突破咸水层之间的泥岩隔层。与CO2晕的运移和压力影响距离相比,温度的影响范围要小很多。
 |
| 图 8 温度变化时空分布特征Fig. 8 Spatial and temporal distribution of change of temperature |
对于侧向为一类定压力边界的模型,用于储存注入的CO2的空间来自:有效应力减小引起的多孔介质的膨胀体积;地层水压力增加导致的地层水压缩体积;从一类边界流出的地层水体积。在注入早期,压力上升还未影响到边界的情况下,CO2被储存在前两种空间里。对于固结成岩的多孔介质,地层压缩和流体压缩能力(大约在10-10 Pa-1数量级上)并不强,注入大量的CO2将引起大范围的压力上升。图 9显示了两种注入方案对R1、R3和R8储层的压力变化。根据井筒“由上至下”的计算方法,得到这3层的注入压力分别为20.7、22.2和23.2 MPa。R1和R8的压力差(23.2-20.7=2.5 MPa)稍微小于其初始状态的压力差(19.8-16.9=2.9 MPa),主要是因CO2密度小于水引起的。压力上升的侧向范围是注入1 a后2 km和10 a后达到7 km,很明显早期压力上升的范围快于后期,主要是因为随着范围的扩大,注入的CO2被“平均”储存到更大的空间中。
 |
| 图 9 压力时空分布特征Fig. 9 Spatial and temporal distribution of pressure |
泥岩中较大的毛细压力将阻止CO2穿透砂岩储层上下的泥岩运移,强制其沿储层水平方向运移。从图 10可以看到CO2的侧向运移最远距离在注入1 a和20 a后分别约为145 和616 m,远远小于压力上升的范围。CO2在第R1、R2和R8储层中的运移速度快,主要是因为其具有较大的渗透率。
 |
| 图 10 CO2饱和度时空变化特征Fig. 10 Spatial and temporal distribution of CO2 saturation |
垂向位移是由压力和温度的变化引起。注入冷的CO2到地层中会引起孔隙水压力的增加和地层温度的降低。孔隙水压力的增加进而引起有效应力的减小,地层会向上隆起,而温度的降低会导致地层的下沉,两种相反的作用共同影响地层的垂向变形。从图 11a可以看到,地表最大隆起约为0.14 m,其位置并不在靠近井的地方,而是离井大概100 m,说明在井附近温度降低引起的地面下沉还是比较大的。从整个区域来看,整个注入期内地面是隆起的,说明地面变形还是压力变化导致起主导作用,隆起范围由注入1 a的2 km扩展到20 a的接近10 km,这个范围变化过程直接对应于压力上升的变化过程。
在水平方向上,由于侧向受限,压力和温度变化均会引起水平有效应力的变化;而在垂向上,地面的自由变形使得垂向有效应力仅仅受压力变化引起,而与温度变化无关。图 11b显示了井附近(x=0.3 m)和远井(x=2 000.0 m)位置注入20 a后的有效应力变化。可以看到,近井位置垂向有效应力在注入层位明显降低,降低幅度为3~4 MPa,水平有效应力在注入层位降低大于垂向有效应力的变化,最大达到6.0 MPa;而在远井位置有效应力整个垂直剖面上变化一致,垂直和水平有效应力降低分别约为1.0 MPa和0.3 MPa。
 |
| 图 11 垂向位移和有效应力时空变化特征Fig. 11 Spatial and temporal distribution of vertical displacement and effective stress |
对于定压力的注入方案,注入速率是场地储存能力评价的一个重要指标。采用注入井井口8.0 MPa和35.0 ℃的注入方案,CO2注入速率约为1.7 kg/s(等效5.4万 t/a),其中注入到储层R8、R2、R1和R7的分别占到注入量的28%,21%,19%和14%,合计达到80%(图 12)。根据储层厚度统计,可以近似认为石千峰和刘家沟储盖层组合能够容纳一半注入的CO2,因此,10万t/a的CO2注入量采用此注入方案能够实现。
 |
| 图 12 CO2注入速率时间变化Fig. 12 Evolution of CO2 injection rate |
3.6 力学引起的渗透率变化
孔隙水压力的增加和地层温度的降低均引起有效应力的减小,从而导致孔隙度和渗透率的增加。从图 13可以看到,整个区域的渗透率在CO2注入后均增加,其中在近井100 m内增加最大,增加了10%~40%,这是因为在此范围压力和温度变化均较大。同时,也可以看到在最下层的储层R8增加最大,主要归因于储层R8的相对较高的初始孔隙度和渗透率使得进入R8储层的CO2较多,温度和压力变化也较大。
 |
| 图 13 力学引起的渗透率变化Fig. 13 Change of permeability induce by mechanics |
图 14显示了考虑不同耦合效应的注入速率。仅考虑水动力过程(H)、耦合的热-水动力过程(TH)、耦合的水动力-力学过程(HM)和耦合的热-水动力-力学过程(THM)的平均注入速率分别为1.66,1.56,1.78和1.76 kg/s,最大和最小之间相差约13%。对比H和TH与HM和THM,可以看到温度效应的影响:在不考虑力学效应时,忽略温度效应后的差别为6%,而考虑力学效应时,忽略温度效应的差别为3%。对比H和HM与TH和THM,可以看到力学效应的影响:在不考虑温度效应时,忽略力学效应后的差别为7%,而考虑温度效应时,忽略力学效应的差别约为13%。由此可见,温度对注入速率起负作用,而力学起正作用,力学正作用大于温度负作用。深层的原因是温度降低而导致流动黏滞系数增加,增加了注入阻力,而有效应力的减小增加了渗透率,减小了注入阻力。
 |
| 图 14 耦合过程对注入速率的影响对比Fig. 14 Comparison of total injection rate for the four models |
1) 基于Terzaghi固结沉降的理论和TOUGH2中的TH耦合模型,建立了THM耦合数学模型,并在TOUGH2的框架中加入了该力学过程,通过与解析解的对比验证了该程序的科学性。
2) 在井口注入压力为8.0 MPa、温度为35.0 ℃时,10 万t/a的注入量基本能够得到保证,其中进入到石千峰第R8、R2、R1和R7层的CO2占到总注入量的80%。
3) 通过THM数值模拟分析了CO2注入后储层中温度、压力、CO2饱和度、位移和有效应力的时空演化特征:压力影响范围最大,注入20 a基本影响到边界;CO2运移的距离其次,注入20 a最大为620 m;温度影响范围最小,注入20 a不到100 m;位移和应力变化主要与压力变化相关,注入引起最大抬升为0.14 m,在注入井附近位置储层中有效应力变化水平方向要大于垂直的,而在远井位置相反。另外,注入引起井附近有效应力明显减小,从而导致了孔隙度和渗透率的增大,增强了CO2注入能力。
4) 忽略力学过程将低估CO2进入到储层,而忽略温度降低将高估其注入,力学的影响明显大于温度的影响。
| [1] | IPCC (Intergovernmental Panel on Climate Change). Carbon Dioxide Capture and Storage[R]. New York: Cambridge University Press, 2005. |
| [2] | IPCC (Intergovernmental Panel on Climate Change). Climate Change 2007: The Physical Science Basis: Contribution of Working Group I to the Fourth Assessment Report of the IPCC[R]. New York: Cambridge University Press, 2007. |
| [3] | Bachu S, Adams J J.Sequestration of CO2 in Geological Media in Response to Climate Change: Capacity of Deep Saline Aquifers to Sequester CO2 in Solution[J]. Energy Conversion and Management, 2003, 44(20): 3151-3175. |
| [4] | Rutqvist J, Wu Y S, Tsang C F, et al. A Modeling Approach for Analysis of Coupled Multiphase Fluid Flow, Heat Transfer, and Deformation in Fractured Porous Rock[J]. International Journal of Rock Mechanics & Mining Sciences, 2002, 39: 429-442. |
| [5] | Rutqvist J, Tsang C F. A Study of Caprock Hydromechanical Changes Associated with CO2 Injection into a Brine Formation[J]. Environmental Geology, 2002, 42: 296-305. |
| [6] | Rutqvist J, Birkholzer J, Cappa F, et al. Estimating Maximum Sustainable Injection Pressure During Geological Sequestration of CO2 Using Coupled Fluid Flow and Geomechanical Fault-Slip Analysis[J]. Energy Conversion and Management, 2007, 48:1798-1807. |
| [7] | Rinaldi A P, Rutqvist J. Modeling of Deep Fracture Zone Opening and Transient Ground Surface Uplift at KB-502 CO2 Injection Well, In Salah, Algeria[J]. International Jounal of Greenhouse Gas Control, 2013, 12:155-167. |
| [8] | Taron J, Elsworth D, Min K B. Numerical Simulation of Thermal-Hydrologic-Mechanical-Chemical Processes in Deformable, Fractured Media[J]. International Journal of Rock Mechanics & Mining Sciences, 2009, 46: 842-854. |
| [9] | 于子望, 张延军, 张庆, 等. TOUGHREACT搭接FLAC3D算法[J]. 吉林大学学报:地球科学版, 2013, 43(1): 199-206. Yu Ziwang, Zhang Yanjun, Zhang Qing, et al. Algorithm of TOUGHREACT Links to FLAC3D[J]. Journal of Jilin University: Earth Science Edition, 2013, 43(1): 199-206. |
| [10] | Winterfeld P H, Wu Y S. Parallel Simulation of CO2 Sequestration with Rock Deformation in Saline Aquifers[C].[S.l.]: SPE Reservoir Simulation Symposium, Society of Petroleum Engineers, 2011. |
| [11] | Hu L T, Winterfeld P H, Fakcharoenphol P, et al. A Novel Fully-Coupled Flow and Geomechanics Model in Enhanced Geothermal Reservoirs[J]. Journal of Petroleum Science and Engineering, 2013, 107:1-11. |
| [12] | Pruess K, Oldenburg C, George M. TOUGH2 User's Guide, Version 2.0[R]. Berkeley: Earth Science Division, Lawrence Berkeley National Laboratory, University of California, 1999. |
| [13] | Pruess K, Garcia J, Kovscek T, et al. Code Intercomparison Builds Confidence in Numerical Simulation Models for Geological Disposal of CO2[J]. Energy, 2004, 29: 1431-1444. |
| [14] | Pruess K, Garcia J. Multiphase Flow Dynamics During CO2 Disposal into Saline Aquifers[J]. Environmental Geology, 2002, 42: 282-295. |
| [15] | Xu T, Sonnenthal E, Spycher N, et al. TOUGHREACT:A Simulation Program for Non-Isothermal Multiphase Reactive Geochemical Transport in Variably Saturated Geological Media: Application to Geothermal Injectivity and CO2 Geological Sequestration[J]. Computers & Geosciences, 2006, 32: 145-165. |
| [16] | 许天福, 金光荣, 岳高凡, 等. 地下多组分反应溶质运移数值模拟:地质资源和环境研究的新方法[J]. 吉林大学学报:地球科学版, 2012, 42(5): 1410-1425. Xu Tianfu, Jin Guangrong, Yue Gaofan, et al. Subsurface Reactive Transport Modeling: A New Research Approach for Geo-Resources and Environments[J]. Journal of Jilin University: Earth Science Edition, 2012, 42(5): 1410-1425. |
| [17] | Pruess K. ECO2N: A TOUGH2 Fluid Property Module for Mixtures of Water, NaCl, and CO2[R]. Berkeley: Earth Science Division, Lawrence Berkeley National Laboratory, University of California, 2004. |
| [18] | 方云, 林彤, 谭松林. 土力学[M]. 武汉: 中国地质大学出版社, 2003. Fang Yun, Lin Tong, Tan Songlin. Soil Mechanics[M]. Wuhan: China University of Geosciences Press, 2003. |
| [19] | Jaeger J C, Cook, N G W, Zimmerman R W.Fundamentals of Rock Mechanics[M].Malden: Blackwell Publishing, 2007. |
| [20] | 任相坤, 崔永君, 步学朋, 等. 鄂尔多斯盆地CO2地质封存潜力分析[J]. 中国能源, 2010, 32(1): 29-32. Ren Xiangkun, Cui Yongjun, Bu Xuepeng, et al. The Potential Analysis of CO2 Geological Storage in Ordos Basin[J]. Energy of China, 2010, 32(1): 29-32. |
| [21] | 吴秀章, 崔永君. 神华10万t/a CO2盐水层封存研究[J].石油学报: 石油加工, 2010(增刊1): 236-239. Wu Xiuzhang, Cui Yongjun. Study on 0.1 Mt/a CO2 Sequestration in Saline Formation[J]. Acta Petrolei Sinica: Petroleum Processing Section, 2010(Sup.1): 236-239. |


