2. 中国地质调查局西安地质调查中心, 西安 710054
2. Xi'an Center of Geological Survey, CGS, Xi'an 710054, China
0 引言
斜坡稳定性问题是岩土工程、工程地质等学科中的重要研究课题之一,目前,斜坡稳定性分析的方法主要包括极限平衡法[1](如Fellenius法、Bishop法、Janbu法、Morgenstern-Price法、Spencer法、Lowe-Karafiath法等)、数值分析法(如强度折减法[2]、离散单元法[3]、流形元法[4]等)、可靠度法[5]、非线性法(如神经网络方法[6]等)、工程地质类比法等。很多方法已在目前的工程实践中得以应用,其中以极限平衡法应用最为广泛。极限平衡法需要事先假定潜在滑动面的形状和位置,将滑体离散为一定数量的条块,假定条块之间存在一定的条间力函数,以稳定系数来表征斜坡的整体稳定性,对斜坡局部或者滑面上某点的稳定度判断存在一定的局限性,而且极限平衡法未能考虑斜坡体内应力集中现象对坡体稳定性的影响。
随着数值模拟方法在斜坡稳定性评价中的广泛应用,越来越多的学者在研究如何将斜坡体应力分布与斜坡稳定系数相结合。Huang等[7]提出了最小安全系数法,以修正的Drucker-Prager强度准则为依据,利用ADINA有限元软件得到了以应力分布为基础的最小安全系数。蒋青青[8]推导了基于Hoek-Brown准则的点安全系数,推导过程极其复杂,适用于岩质边坡。樊赟赟等[9]从理论上推导了定义三维广义Mohr空间中的点安全系数,但其公式复杂且较难应用于实际工程,且未进行实例验证。杨涛等[10]定义了滑面单元点安全系数,这也就意味着需要事先确定滑面单元来计算滑坡稳定系数。郑文棠[11]采用FLAC3D软件对比了强度折减法和点安全系数法,但未探讨与极限平衡法之间的关联。Lu Ning等[12]采用局部稳定系数法分析了降雨诱发型滑坡的稳定性。
综上所述,众多学者从不同角度对点安全或点稳定系数进行了研究并定义了其概念,但推导的计算公式都比较复杂,应用于实际工程较为困难,且未与传统极限平衡法进行对比分析。因此,为了弥补目前对点稳定系数研究的不足,笔者以简明的几何关系推导点稳定系数计算公式,界定点稳定系数概念,将点稳定系数法与有限元应力分布分析结合起来,探讨深层次的斜坡稳定性分析评价方法;并与传统极限平衡法进行对比分析,以期为斜坡稳定性评价提供一定的理论指导。
1 点稳定系数定义点稳定系数是指用来衡量斜坡体内岩土体单个质点稳定程度的尺度。它的大小与该点处岩土体的黏聚力c、内摩擦角φ、重度γ、弹性模量E和泊松比μ等定参量条件下所对应的应力状态(最大主应力和最小主应力)有关。
以莫尔-库伦强度理论为依据,则斜坡体内某一点所受的应力如图 1中实线圆所示,该点的应力(实线圆)与莫尔-库伦破坏包络线的关系决定了该点的应力状态是否稳定,该点的稳定系数可表达为

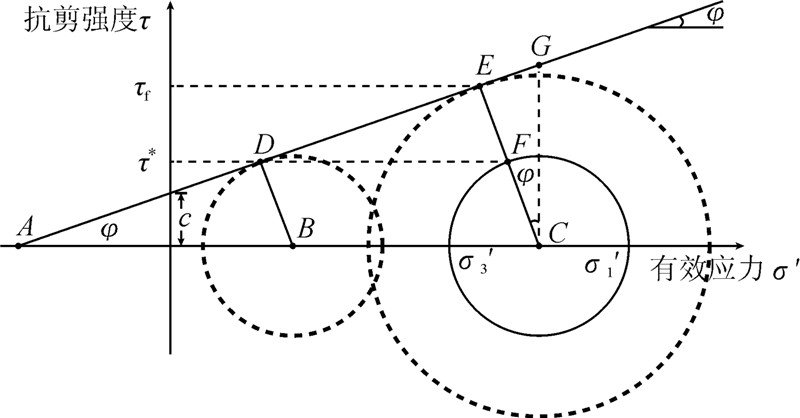 |
| 图 1 点稳定系数定义示意图 Fig. 1 Illustration of the concept of local factor of safety |
| |
将实线圆向左平移至与莫尔-库伦破坏包络线相切于D点,使得CF//BD,延长CF至E点。此时,E点在纵坐标上的投影为该点潜在抗剪强度值τf;F点在纵坐标上的投影为该点当前状态下的剪应力τ*。
图 1中,根据三角形相似原理可知△ABD∽△ACE,则
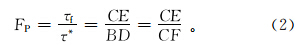
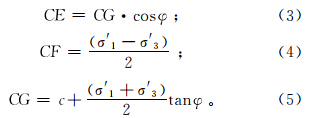
将式(3)、(4)、(5)代入式(2)可得
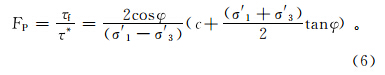
定义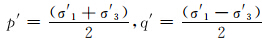 ,则式(6)可变为
,则式(6)可变为
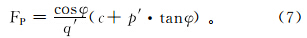
在斜坡体内二维空间内任意一点的点稳定系数可用式(7)计算求得。由图 1可知,当斜坡体内点剪应力低于莫尔-库伦破坏包络线时,点稳定系数FP大于1.00;而当斜坡体内点剪应力接近或与莫尔-库伦破坏包络线相切时,点稳定系数FP等于1.00。因此,点稳定系数可勾绘斜坡体内稳定或不稳定的区域。
2 点稳定系数法介绍
在斜坡稳定性评价中,大多采用极限平衡法,且一般假设或指定某一形状(圆弧形、对数螺旋形对数、折直线形等)的滑面分析斜坡稳定性。这种方法的计算过程相对简单方便,但不能够体现斜坡体内的应力集中现象,而应力集中或应力状态改变往往是斜坡失稳的关键因素。
点稳定系数法是指在分析斜坡体内各点应力状态的基础上,按式(7)计算坡体内各点的点稳定系数,进而勾绘出斜坡体内稳定或不稳定的区域,以此来分析评价斜坡稳定性的方法。点稳定系数法不用指定或假设滑面,可以考虑到坡体内应力集中或应力状态改变对斜坡稳定性的影响,但计算过程相对复杂一些。
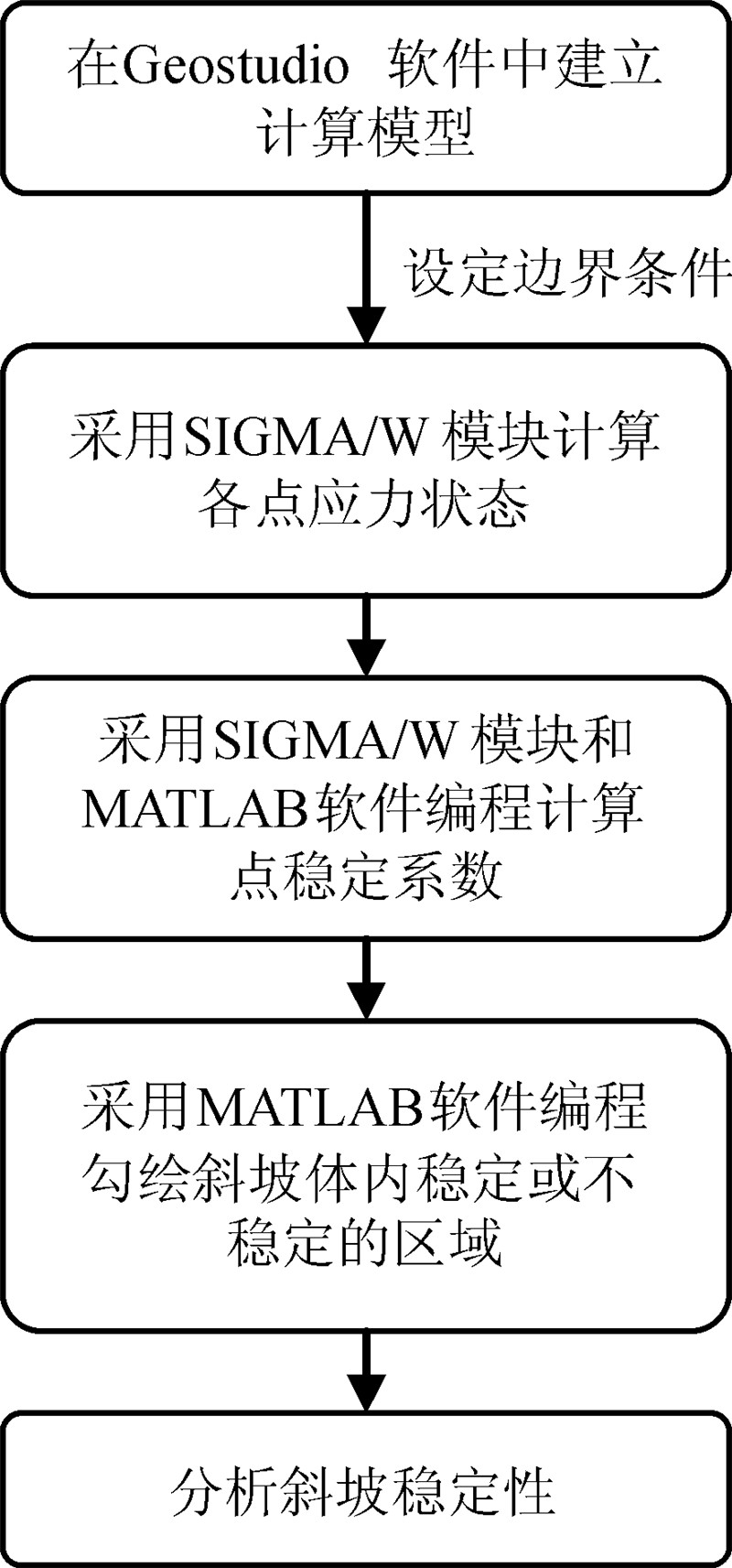
具体计算过程如图 2所示。在斜坡坡形基础上,首先在Geostudio软件中建立计算模型,设置岩土体参数(黏聚力、内摩擦角、重度、弹性模量和泊松比),设定边界条件,计算模型中各点的应力状态并导出应力值;然后在MATLAB软件中,按式(7)计算各点稳定系数,对各点的稳定系数进行插值,勾绘出斜坡体内稳定或不稳定的区域;最后分析评价斜坡稳定性。
 |
| 图 2 计算过程示意图 Fig. 2 Framework of the calculation process |
| |
为了对比点稳定系数法与极限平衡法在计算过程与计算结果表达形式上的不同,设计了不同的计算方案:设计边坡模型坡度为90°、60°、45°条件下,分别采用点稳定系数法与极限平衡法进行计算对比分析。由于计算模型采用的是均质土坡,因此选用适合圆弧滑动面的简化Bishop法计算,该方法理论简单,和其他极限平衡法的结果接近。利用Geostudio软件中的SLOPE/W模块中的简化Bishop法进行边坡安全系数计算。
为了使在不同坡度(90°、60°、45°)条件下不同计算方法的计算结果具有对比性,不同坡度计算过程中的岩土体参数不变,具体如下:黏聚力c为20 kPa;内摩擦角φ为30°;重度γ为16 kN/m3;弹性模量E为21 000 kPa;泊松比μ为0.25。
3.1 直立斜坡(90°坡)
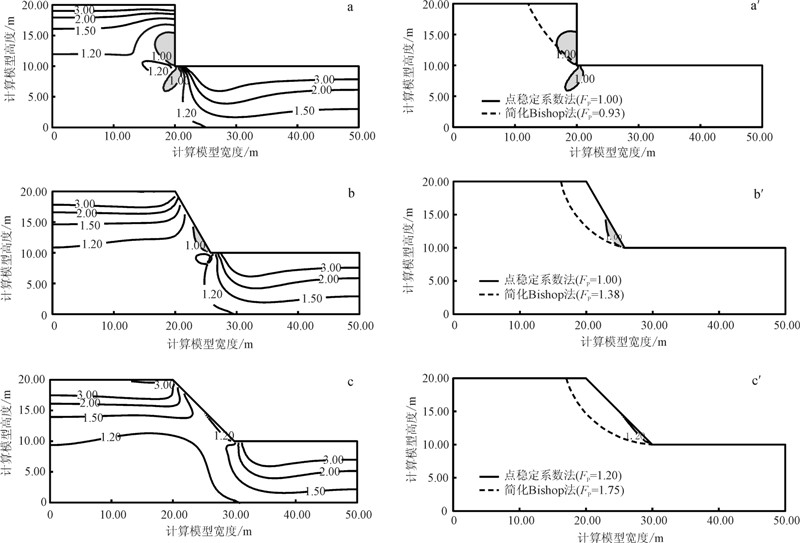
首先,利用Geostudio软件SIGMA/W模块计算直立坡体内各点的应力值,并基于各点的应力值和岩土参数,采用公式(7)进行点稳定系数的计算,绘制出直立斜坡的点稳定系数等值线图(图 3a)。由图 3a可知,在坡脚(第一区域)和坡脚底部(第二区域)存在有两处潜在的不稳定区域(即点稳定系数小于1.00的区域,图 3a,a′,b,b′中的灰色区域),这两个区域均为应力集中区,剪应力较大,在第一区域内最大主应力方向为垂直方向,而在第二区域内最大主应力方向为水平方向。第一区域不稳定的范围由坡脚向左上方大约沿60°(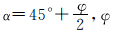 为土体内摩擦角,文中φ=30°)的斜线方向破坏,即朗肯主动土压力破裂面,这与大量室内模型试验和足尺试验结果也相一致。
为土体内摩擦角,文中φ=30°)的斜线方向破坏,即朗肯主动土压力破裂面,这与大量室内模型试验和足尺试验结果也相一致。
 |
| 图 3 点稳定系数等值线图及与极限平衡法计算结果对比图 Fig. 3 Contour map of local factor of safety and comparison with limit-equilibrium method |
| |
为了与极限平衡法计算结果的对比,将点稳定系数等值线图中点稳定系数等于1.00的线勾画出来,与简化Bishop法计算的潜在滑动面进行对比,如图 3a′所示。由图 3a′可知:简化Bishop法计算潜在滑动面的稳定系数为0.93,坡体均处于不稳定状态;而点稳定系数法计算得到的点稳定系数小于1.00的区域包括了两个区域。
这两种方法最基本的区别在于点稳定系数等于1.00的面内每个点均处于不稳定状态,而极限平衡法的潜在滑动面上并不是每个点都已达到土体的抗剪强度值,且不稳定的区域范围大小也不一样。
3.2 60°斜坡由60°斜坡的点稳定系数等值线图(图 3b)可知,同样的岩土体参数,只在坡脚处存在有潜在不稳定区域,在其他区域各点点稳定系数均大于1.00。
同样将点稳定系数等值线图中点稳定系数等于1.00的线勾画出来,与简化Bishop法计算的潜在滑动面进行对比,如图 3b′所示。由图 3b′可知:简化Bishop法计算潜在滑动面的稳定系数为1.38,坡体均处于稳定状态;而点稳定系数法计算得到坡脚处一定区域内处于不稳定状态。这也就意味着点稳定系数法比极限平衡法在预测破坏面上增加了准确度和敏感性。
3.3 45°斜坡由45°斜坡的点稳定系数等值线图(图 3c)可知,坡体内各点的点稳定系数均大于1.00。将点稳定系数等值线图中点稳定系数等于1.20的线勾画出来,与简化Bishop法计算的潜在滑动面进行对比,如图 3c′所示。简化Bishop法计算潜在滑动面的稳定系数为1.75,坡体均处于稳定状态。点稳定系数法与极限平衡法的计算结果具有一致性。
4 点稳定系数法影响因素分析由点稳定系数的定义可知,斜坡体内岩土体所在位置的应力场和岩土体力学参数是点稳定系数法重要的影响因素,现分析如下。
4.1 岩土体所在位置应力场影响分析
斜坡体内应力场的形成和分布与岩土体的沉积环境、受荷历史和构造运动史等有着密切的联系。在利用数值软件计算岩土体应力场分布时,弹性变形范围内计算参数有重度、弹性模量和泊松比。弹性模量的变化主要影响着位移变形,对应力场的分布影响不大;影响应力场分布的参数主要是重度和泊松比。一旦坡形定下来,在岩土体材料不变和无外力作用的情况下,坡体内的应力场分布也就定下来了,点稳定系数分布即可得到。
4.2 岩土体力学参数影响分析以60°斜坡为例,假设黏聚力c和内摩擦角φ之间不相关,分析两者对点稳定系数法和极限平衡法计算结果的敏感性。
4.2.1 黏聚力c的敏感性分析
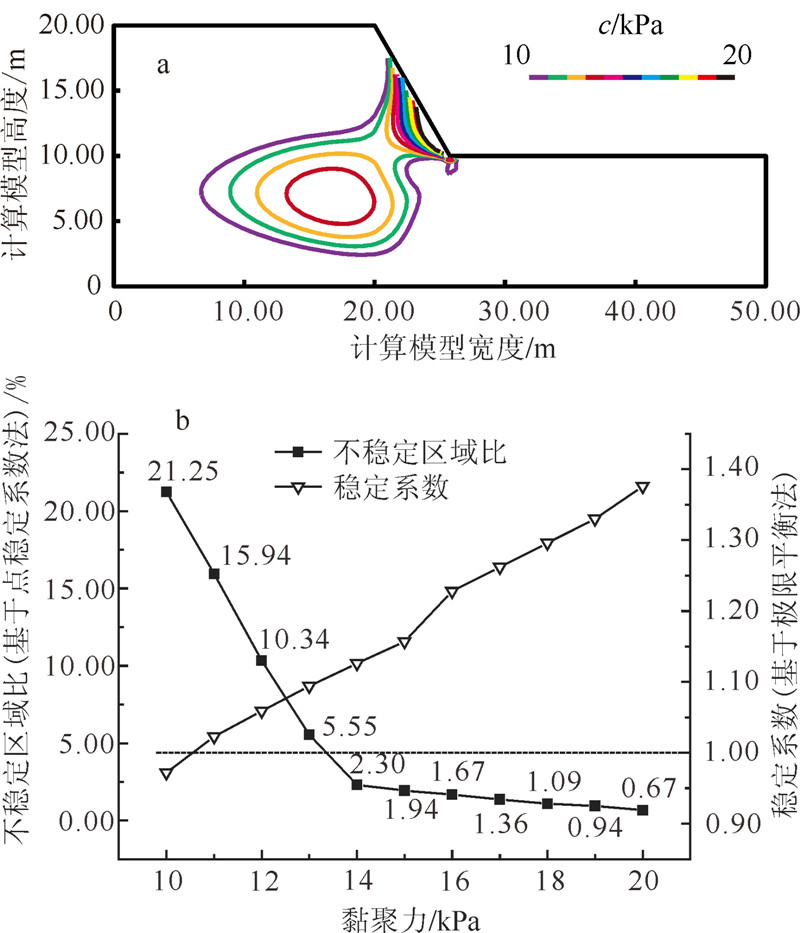
由于点稳定系数法是以点面来表征计算结果的,因此用不稳定区域比,即不稳定区域面积(点稳定系数小于1.00的范围)与整个计算区域面积的比值,分析黏聚力c对计算结果敏感性;而极限平衡法用稳定系数来分析黏聚力c对计算结果敏感性。计算结果如图 4所示。
 |
| 图 4 黏聚力c的敏感性分析图 Fig. 4 Sensitivity analysis of cohesion |
| |
由图 4a可知,当黏聚力c由20 kPa降低到10 kPa时,基于点稳定系数法计算得到的不稳定区域分布从坡脚开始慢慢向坡体内扩大;当黏聚力小于14 kPa时,在坡脚和坡体内部同时出现了不稳定区域,在坡脚形成破坏滑动面,而在坡体内形成压缩变形破坏,在坡顶面呈现沉降现象。
由图 4b可知:当黏聚力c由20 kPa降低到10 kPa时,基于点稳定系数法计算得到的不稳定区域比例从0.67%升至21.25%,且曲线呈非线性变化,曲线先平缓后陡升;黏聚力c在约14 kPa处曲率变化较大,曲线发生明显的偏转,该点定义为点稳定系数黏聚力界限点。当黏聚力大于14 kPa时,不稳定区域比例较小,在斜坡坡脚等区域发生较小范围的破坏;当黏聚力小于14 kPa时,不稳定区域比例明显增大,斜坡则发生大范围的变形破坏。
对于极限平衡法来说,当黏聚力从10 kPa增加到20 kPa时,简化Bishop法计算的稳定系数由0.97增加到1.38,曲线均呈近线性变化,当黏聚力小于11 kPa时,稳定系数小于1.00(图 4b)。
可见,点稳定系数法对黏聚力c的变化更为敏感,存在黏聚力界限点。
4.2.2 内摩擦角φ的敏感性分析
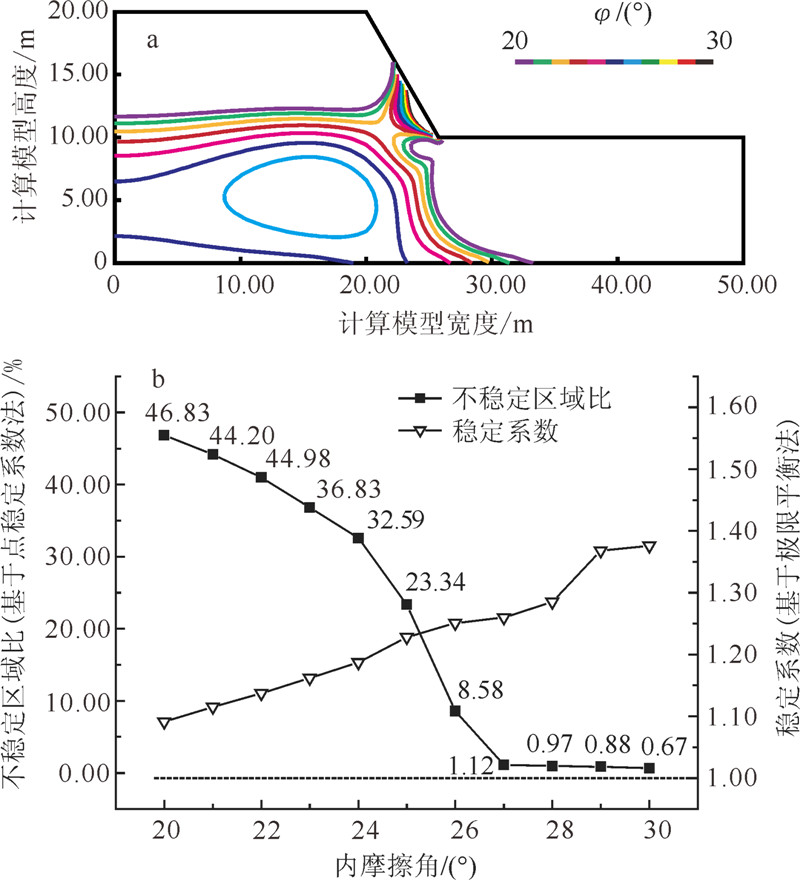
由图 5a可知:当内摩擦角φ的变化范围由30°降低到20°时,基于点稳定系数法计算得到的不稳定区域分布从坡脚开始慢慢向坡体内扩大;当内摩擦角小于27°时,在坡脚和坡体内部同时出现了不稳定区域;当内摩擦角小于23°时,坡体内成片出现不稳定区域,此时已不是斜坡稳定性的范畴,而是坡体整体发生沉降变形破坏。
 |
| 图 5 内摩擦角φ的敏感性分析图 Fig. 5 Sensitivity analysis of internal friction angle |
| |
由图 5b可知:当内摩擦角φ的变化范围由30°降低到20°时,基于点稳定系数法计算得到的不稳定区域比例从0.67%升至46.83%,且敏感性曲线呈非线性变化;内摩擦角φ在小于27°时曲率较大,约在27°处曲线发生明显的偏转,该点定义为点稳定系数内摩擦角界限点。当内摩擦角大于27°时,不稳定区域比例相对较小,在斜坡坡脚等区域发生较小范围的变形破坏;当内摩擦角小于27°时,不稳定区域比例明显增大,斜坡则发生大范围的压缩变形破坏。
对于极限平衡法来说,当内摩擦角从20°增加到30°时,简化Bishop法计算的稳定系数由1.09增加到1.38,曲线均呈近线性变化,稳定系数均大于1.00(图 5b)。
可见,点稳定系数法对内摩擦角φ的变化也更为敏感,存在内摩擦角界限点。
综上所述,岩土体力学参数对点稳定系数法影响更加敏感一些,尤其是内摩擦角φ的变化,存在黏聚力界限点和内摩擦角界限点,且对均质斜坡破坏形式(局部滑动变形破坏或整体压缩变形破坏)起着非常重要的作用。
5 讨论文中的点稳定系数是在莫尔-库伦强度理论框架下得到的,当然也可根据Fredlund和Lu Ning提出的扩展莫尔-库伦强度理论[1, 12]进行公式推导,如果岩土体材料符合其他破坏准则,也可在点稳定系数定义的基础上进行计算公式推导。
在不同坡度(90°、60°、45°)的均质斜坡条件下点稳定系数法与极限平衡法的计算结果对比中,点稳定系数法不需要假设或指定某一形状滑面进行斜坡稳定性评价,且可考虑应力集中对坡体稳定性的影响,以不稳定区域表达计算结果,但在计算得到的不稳定区域里可能发生的是滑动变形破坏,也有可能发生的是压缩变形破坏。在应力集中部位易出现不稳定区域,与极限平衡法中潜在滑动面概念有所区别,计算结果表达含义也有所不同。因此在利用点稳定系数法计算斜坡稳定性时,应准确地刻画计算模型的边界条件和坡体应力分布特征。
在点稳定系数法影响因素分析中,岩土体参数的变化对点稳定系数法计算的结果更为敏感,界限点(黏聚力界限点和内摩擦角界限点)可用于判断均质斜坡破坏形式(局部滑动变形破坏或整体压缩变形破坏)。对于均质斜坡,同一岩土参数条件下极限平衡法计算结果为稳定,而点稳定系数法计算结果为沉降变形(整体压缩变形破坏),这也很好地说明了填方边坡或路基主要的病害之一为局部或整体沉降变形破坏。
文中没有考虑外部加荷或者开挖卸荷对应力场分布的影响。利用数值软件计算应力场时,只要是边界条件明确,计算受荷或卸荷条件下的应力场分布相对容易,这是数值软件的优势所在,也是基于数值软件的点稳定系数法在考虑外部加荷或者开挖卸荷时,比极限平衡法的优势所在。
6 结论1)对直立斜坡,两种方法的计算结果均为不稳定,但点稳定性系数法勾绘出坡脚及坡脚底部存在有两处不稳定区域。点稳定系数等于小于1.00的区域内每个点均处于破坏状态,而极限平衡法的潜在滑动面上并不是每个点都已达到土体的抗剪强度值,且不稳定的区域范围大小也不一样。
2)对60°斜坡,点稳定系数法计算的结果为只在坡脚处存在有软弱或潜在不稳定区域,在其他区域各点点稳定系数均大于1.00;而极限平衡法计算得到的结果为潜在滑动面的稳定系数均大于1.00,坡体均处于稳定状态。
3)对45°斜坡,点稳定系数法与极限平衡法计算得到的结果为坡体均处于稳定状态,两种方法计算结果具有一致性。
4)点稳定系数法不需要假设或指定某一形状的滑面进行斜坡稳定性评价,以不稳定区域表达计算结果,且可考虑应力集中对坡体稳定性的影响。
5)在分析了岩土体所在的应力场因素和岩土体力学参数因素对点稳定系数法计算结果的敏感性后发现:相对于极限平衡法,岩土体力学参数对点稳定系数法影响更为敏感,存在黏聚力界限点和内摩擦角界限点,且对均质斜坡破坏形式(局部滑动变形破坏或整体压缩变形破坏)起着非常重要的作用。
| [1] | Fredlund D G, Rahardjo H. Soil Mechanics for Un-saturated Soils[M]. New Jersey: John Wiley & Sons Press, 1993. |
| [2] | 年廷凯, 张克利, 刘红帅, 等.基于强度折减法的三维边坡稳定性与破坏机制[J].吉林大学学报:地球科学版, 2013, 43(1): 178-185. Nian Tingkai, Zhang Keli, Liu Hongshuai, et al. Stability and Failure Mechanism of Three-Dimensional Slope Using Strength Reduction Method[J]. Journal of Jilin University: Earth Science Edition, 2013, 43(1): 178-185. |
| [3] | 徐寅, 陈胜宏. 基于离散单元法的滑坡堆积及其涌浪计算[J]. 岩土力学, 2012, 33(9): 2850-2856. Xu Yin, Chen Shenghong. Calculation of Heap Shape of Landslide and Its Surge Based on Discrete Element Method[J]. Rock and Soil Mechanics, 2012, 33(9): 2850-2856. |
| [4] | 张国新, 赵妍, 石根华, 等. 模拟岩石边坡倾倒破坏的数值流形法[J]. 岩土工程学报, 2007, 29(6):800-805. Zhang Guoxin, Zhao Yan, Shi Genhua, et al. Toppling Failure Simulation of Rock Slopes by Numerical Manifold Method[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(6): 800-805. |
| [5] | 马建全, 李广杰, 张文, 等.基于可靠度的边坡稳定性影响因素[J]. 吉林大学学报:地球科学版, 2011, 41(增刊1): 187-194. Ma Jianquan, Li Guangjie, Zhang Wen, et al. Factors of Slope Stability Based on the Reliability Analysis[J]. Journal of Jilin University: Earth Science Edition, 2011, 41(Sup.1): 187-194. |
| [6] | 张晨, 陈剑平, 肖云华.基于神经网络对有限元强度折减法分析[J].吉林大学学报:地球科学版, 2009, 39(1): 114-118. Zhang Chen, Chen Jianping, Xiao Yunhua. Analysis on Theory of Strength Reduction FEM Based on Artificial Neural Networks[J]. Journal of Jilin University: Earth Science Edition, 2009, 39(1): 114-118. |
| [7] | Huang S, Yamasaki K. Slope Failure Analysis Using Local Minimum Factor-of-Safety Approach[J]. Journal of Geotechnical Engineering, 1993, 119(12), 1974-1989. |
| [8] | 蒋青青. 基于Hoek-Brown准则点安全系数的边坡稳定性分析[J]. 中南大学学报:自然科学版, 2009, 40(3): 786-790. Jiang Qingqing. Stability of Point Safety Factor of Slope Based on Hoek-Brown Criterion[J]. Journal of Central South University: Science and Technology, 2009, 40(3): 786-790. |
| [9] | 樊赟赟, 王思敬, 王恩志, 等. 岩土材料剪切破坏点安全系数的研究[J]. 岩土力学, 2009, 30(增刊2): 200-203. Fan Yunyun, Wang Sijing, Wang Enzhi, et al. Research on Point Safety Factor of Shear Failure Geomaterials[J]. Rock and Soil Mechanics, 2009, 30(Sup.2):200-203. |
| [10] | 杨涛, 周德培, 马惠民, 等. 滑坡稳定性分析的点安全系数法[J]. 岩土力学, 2010, 31(3): 971-975. Yang Tao, Zhou Depei, Ma Huimin, et al. Point Safety Factor Method for Stability Analysis of Landslide[J]. Rock and Soil Mechanics, 2010, 31(3):971-975. |
| [11] | 郑文棠. 基于FLAC3D的强度折减法和点安全系数法对比[J].水利与建筑工程学报, 2010, 8(4):54-57. Zheng Wentang. Contrast on Strength Reduction Method and Point Safety Factor Method with FLAC3D[J]. Journal of Water Resources and Architectural Engineering, 2010, 8(4): 54-57. |
| [12] | Lu Ning, Şener-Kaya B, Wayllace A, et al. Analysis of Rainfall-Induced Slope Instability Using a Field of Local Factor of Safety[J]. Water Resource Research, 2012, 48: W09524. |


