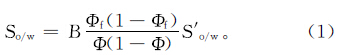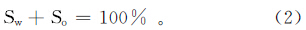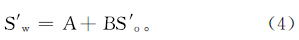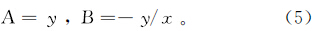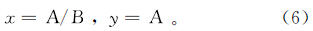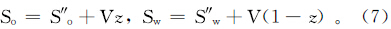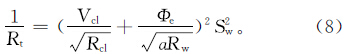准确计算含水饱和度是储层定量评价的难题之一,尤其是针对泥质重、束缚水含量高、地层物性差、低孔、低渗、低产能且孔隙结构复杂的低阻油层。这种油层普遍具有低含油饱和度的特点,在评价时难以合理选择饱和度模型并确定其真实的含油饱和度,导致储量计算不准、流体性质判别以及产能预测遇到困难[1, 2]。目前,在泥质砂岩中根据泥质分布形式建立的饱和度模型大多采用体积模型与电阻并联理论,都带有区域性和经验性[3],至今仍没有一种模型被实践所肯定,能够作为合理的通用模型适用于所有区域。因此,笔者首先分析珠江口盆地低阻油层的测井响应特征,在充分考虑影响密闭取心饱和度各种因素的基础上,对测量的油、水饱和度进行压实、脱气以及漏失等校正[4, 5],进而对测井计算的含水饱和度进行标定,以确定最适合本区域地质条件的饱和度模型。 1 珠江口盆地低阻油层测井响应特征及地质成因
珠江口盆地存在大量的低阻油层,其岩性主要为油斑、油浸泥质粉砂岩,泥质体积分数平均在30%以上,物性较差,气测有异常显示,典型水层的电阻率小于1.1 Ω·m,低阻油层的电阻率为1.0~1.3 Ω·m,较本区典型的油层(大于10.0 Ω·m)小,与相邻泥岩和水层相近。
通过对粒度、黏土矿物、薄片以及扫描电镜等岩心资料的分析可知,储层岩石颗粒整体较细,黏土矿物主要以伊利石和伊蒙混层为主,含高岭石和绿泥石。一方面,以蒙脱石为代表的黏土矿物具有很高的阳离子交换容量,会导致地层出现附加导电性;另一方面,这些黏土矿物具有很强的吸水膨胀性,造成黏土束缚水大量增加,加之微孔隙发育,会形成以束缚水为主要成分的导电网络,这是导致本区油层低阻的主要原因。
针对本区的低阻油层,利用同一套储层参数进行处理,发现不同的饱和度模型计算的结果存在较大差异。为了确定储层的真实含油饱和度,在低阻油层段进行了密闭取心,并增加了核磁共振测井。这些资料为测井解释结果的标定以及区域饱和度模型的确定提供了强有力的依据。 2 密闭取心饱和度分析及校正 2.1 密闭取心饱和度影响因素分析
利用密闭取心资料确定地层含油、水饱和度是目前最直接有效的方法,但在岩心上提的过程中,往往存在以下几个方面的问题:1)由于降温、降压导致的脱气;2)油、水的漏失;3)取心的过程实际上是卸压的过程,压力降低,岩心的骨架体积、孔隙体积和外观体积必然增大,岩心会产生体积膨胀;4)取心密闭性不好,有泥浆渗入;5)取样及实验过程中由于等待时间造成的吸水和油气挥发[6, 7]。由于这些因素的影响,实验室测量的岩心油、水饱和度往往较实际偏小。本区低阻油层段岩心分析的含油饱和度(S′o)与含水饱和度(S′w)之和主要为70%~90%(图 1),所以需要针对以上一些影响因素对岩心油、水饱和度进行校正,且校正后的油、水饱和度之和应为1。
 |
| 图 1 珠江口盆地低阻油层段岩样饱和度统计 Fig. 1 Core sample saturation statistics in low resistivity reservoir in the Pearl River Mouth basin |
| |
根据前人[8]的实验成果,对于纯油层,在降压和脱气的过程中,没有水从岩样中流出,只有部分原油流出,这是因为岩样中没有自由水,且束缚水存在于颗粒表面的水膜或储存于细小孔隙中的毛管滞水;而对于强水淹层或纯水层来说,没有油从岩样中流出,只有自由水流出,因为地层中的残余油也是无法移动的。因此,针对不同流体性质的密闭取心岩样,其含油、含水饱和度的校正方法是不同的。
低阻油层岩样在上提的过程中,其含水体积是不变的,但岩心的骨架体积和孔隙体积增大,造成实测的岩心含水饱和度偏小,因此需对岩心含水饱和度进行覆压校正[9],可得到地层条件下岩样的含水饱和度,进而得到含油饱和度。同理,对于强水淹或纯水层,只需对岩心含油饱和度进行覆压校正,即可得到地层条件下岩样的含水饱和度。
经覆压校正后,岩样的含水饱和度会有不同程度的增加,增加量的大小与覆压孔隙度和地面孔隙度之间的差异有直接关系。岩心饱和度的覆压校正公式为
其中:Φf、Φ分别为覆压孔隙度和地面孔隙度;B为体积系数,指原油在地下的体积与其在地面脱气后的体积之比,是对含油饱和度做脱气校正,对油来说B>1,对水来说,B≈1;So/w、S′o/w分别为覆压校正后和实测的岩心含油/水饱和度;Φf/Φ为针对孔隙体积增大的校正;(1-Φf)/(1-Φ)为针对岩石总体积和骨架体积膨胀的校正。当地层为弱-中水淹或油水同层时,在岩心上提的过程中油、水均存在漏失,二者饱和度均有减小,因此在进行覆压校正的基础上,还需进行油、水漏失的校正。针对油水漏失校正,业界还没有形成权威的处理方法,但目前使用最广泛且效果较好的是统计法。
利用统计法进行校正的理论基础[10, 11]是:对于同一口井,在各种外界影响条件,如取心井段压力、温度、取心工艺、饱和度工艺等基本相同的条件下,从取心到最终得到岩心分析数据的过程中,如果按油、水饱和度进行分区间分析,则油、水损失率为常数。
由于本区主要为油水层,孔隙中只有油和水两相,在原始地层中油、水饱和度应满足
式中:So和Sw分别为地层原始含油和含水饱和度。设原油剩余率为常数c,水剩余率为常数d,则
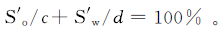
从理论上来讲,不同岩性中的油水饱和度关系会有所不同,但由于本区低阻油层岩性均为泥质粉砂岩,因此可合并进行分析。将岩心实验分析得到的含油、水饱和度之和以5%为步长进行分类,从60%到100%共分为8个区间,在每个区间内对数据点进行线性回归,结果如图 2所示。油、水饱和度在各区间都存在着很好的线性关系,其关系可表达为
式中:A为截距;B为斜率。  |
| 图 2 覆压校正后岩心油水饱和度分区间关系图 Fig. 2 Diagram in different intervals of core water-oil saturation which has done the overburden pressure correction |
| |
由于式(3)和式(4)表征同一物理意义,则
则有 其中,A、B可从不同饱和度区间的线性回归关系式中获得(图 2)。如表 1所示,A、B值在不同油水饱和度区间内会有一定的差别。总的来看,A、B值主要受到两方面因素的影响:一是饱和度分类步长的选取标准,分类越细,步长越短,则线性拟合的相关性越好,得到的参数也越精确;二是密闭取心样品点在各饱和度区间内分布的数量,样品点越多,则拟合的结果越有代表性,反之如果在某个区间的点过少,则拟合的结果可能会出现较大的偏差。实际上,此二者在某种程度上是相互制约的,分类过细必然导致饱和度区间内可供拟合点的数量减少,因此饱和度的分类标准不是固定的,而是根据样品点油、水饱和度的分布情况来选取合适的分类步长,在分类尽可能细的基础上又要保证每个区间内有足够多的数据点。目前笔者是按照5%的步长对饱和度进行分类处理。需要说明的是:拟合得到的A、B值只适合在本井用于岩心流体漏失的校正;而对于其他区域,在有密闭取心资料的情况下,可利用同样的处理方法,得到合适的A、B值。
| 饱和度/% | A | B |
| 60~65 | 62.83 | -0.987 |
| 65~70 | 65.86 | -0.955 |
| 70~75 | 71.38 | -0.997 |
| 75~80 | 77.98 | -1.02 |
| 80~85 | 82.44 | -0.991 |
| 85~90 | 87.48 | -0.996 |
| 90~95 | 93.64 | -1.034 |
| 95~100 | 100.78 | -0.984 |
在此基础上,根据式(6)就可得到c和d的值,进而得到岩样油、水饱和度的校正量。
经校正后,岩心油、水饱和度之和均在100%左右,因此还需要对数据进行归一化处理。设校正后的含油、水饱和度分别为S″o、S″w,含油、水饱和度的总损失量为V,含油饱和度占总流体饱和度的比例为z,则有
经归一化校正后,岩样的油、水饱和度之和即为100%。
图 3为珠江口盆地低阻油层和油水同层段岩心含油饱和度校正前后的对比图,可以看到,校正后的岩心含油饱和度较原始岩心分析的含油饱和度明显增加。而对于物性较好、孔隙度较大的岩心,其流体漏失往往较多,校正的量也较大。根据上述原则,对全区低阻油层段的密闭岩心饱和度进行校正,并以校正后的结果来对测井解释的含水饱和度进行标定。
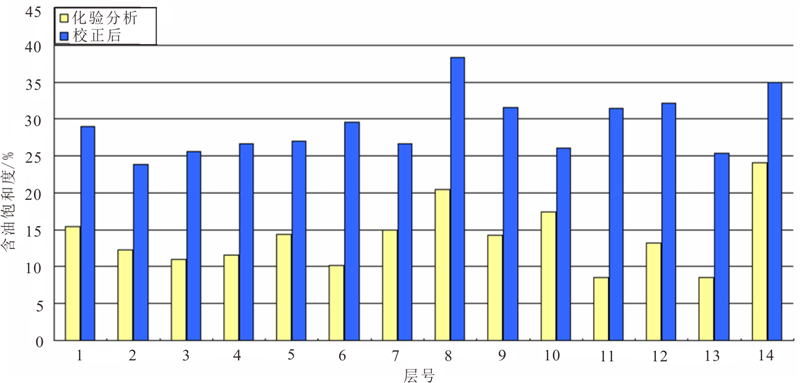 |
| 图 3 岩心分析与最终校正后的含油饱和度对比 Fig. 3 Comparison of the core analysis oil saturation and the corrected oil saturation |
| |
针对各种复杂地层和特定区域的地层,国内外诸多学者提出了很多针对泥质砂岩储层的饱和度模型,它们均不同程度地考虑了地层泥质分布、微观孔隙结构特征和不同导电形式的影响。一般来说,传统的Archie公式在泥质较少的纯砂岩地层中能够很好地评价地层含水饱和度,但在泥质较重的地层中,计算的含水饱和度误差较大,其应用受到了很大的限制。目前,业内主要基于大量的岩心物理实验,通过精心设计的实验流程,研究不同条件下胶结指数(m)和饱和度指数(n)的变化规律,
来定量评价低阻油层的饱和度[12]。印度尼西亚公式适用于较低地层水矿化度以及泥质体积分数小于50%的泥质砂岩,具有泥质导电影响校正功能,在很多地区的饱和度评价中得到了很好的应用。Simandoux改进公式是在原方程的基础上由Schlumberger公司推出的,它不考虑泥质的分布形式,只考虑总的混合泥质含量,是比较常用的泥质砂岩饱和度计算模型。Waxman-Smits模型对各种地层水矿化度的地层都适用,但这种方法需要以阳离子交换量岩心实验作为支撑,主要考虑地层中黏土水阳离子交换量对电阻率的影响[13, 14]。
以上饱和度方程应用了体积模型和电阻率并联的概念,但在推导电阻率和含水饱和度的计算公式中,都做了一些假设(如地层岩性、物性和地层水性质基本不变等),从某种程度上来说,它们的应用都带有一定的经验性,在一定条件下适用于某些地层饱和度的计算。但由于实际地层的微观和宏观导电特性往往受到多重因素的影响,目前对其特征还缺乏深入的研究,单从方程的提出背景以及不同的导电机理等方面出发,在生产实际中仍然难以合理地选择饱和度模型。因此,对于不同地区、不同特征以及不同地质成因的地层,应尝试利用多种饱和度模型进行计算和综合分析,经岩心资料以及核磁解释成果标定后,优选出最适合于本区的饱和度模型[15]。
参考珠江口盆地的其他油田,虽然没有密闭取心资料,但利用常规取心岩样的压汞数据,经处理可得到不同油柱高度下对应的含水饱和度;根据岩样所处的油柱高度,就可知此深度的含水饱和度。以此方法来标定测井计算的结果,长期的研究表明,印度尼西亚公式适合于珠江口盆地大部分地区典型油气层饱和度的评价。
印度尼西亚公式的表达式如下:
其中:Rt,Rcl,Rw分别为地层深电阻率、泥岩电阻率和地层水电阻率,Ω·m;Vcl为泥质体积分数;a为区域岩电参数;Φe为有效孔隙度。对于本区泥质很重的低阻油层来说,多井的DST(drill stem test)结果显示日产油平均为20~50 m3/d,但目前还没有一个确定的饱和度模型。参照适合于大部分地区的印度尼西亚公式,算得的含水饱和度高达70%~80%。很多人认为在如此高的含水饱和度条件下不可能出油,其结果的可靠性受到质疑。因此需要对各种饱和度方程的适用性进行重新验证和标定,并找出最适合本区低阻油层的饱和度模型。 4 低阻油层饱和度综合评价
对珠江口盆地的低阻油层段进行处理,结果如图 4和图 5所示。常规测井曲线计算的地层泥质体积分数和孔隙度均利用岩心分析资料进行了标定,二者总体吻合较好。利用Archie、双水模型、尼日利亚公式、印度尼西亚公式、西门杜公式、Waxman-Smits等多种常用于泥质砂岩地层的饱和度模型进行计算,在泥质很重的低阻油层段,各种饱和度模型计算的结果相差很大;利用密闭取心饱和度进行标定,发现印度尼西亚公式计算的结果与之吻合最好。为了进一步验证此结果,考虑利用核磁共振测井解释的结果来进行辅助标定。
 |
| 英尺(ft)、英寸(in)为非法定计量单位,1 ft=0.304 8 m,1 in=2.54 cm,下同。图4 X1井低阻油层饱和度评价成果图 图 4 X1井低阻油层饱和度评价成果图 Fig. 4 Results figure of low resistivity reservoir saturation evaluation in well X1 |
| |
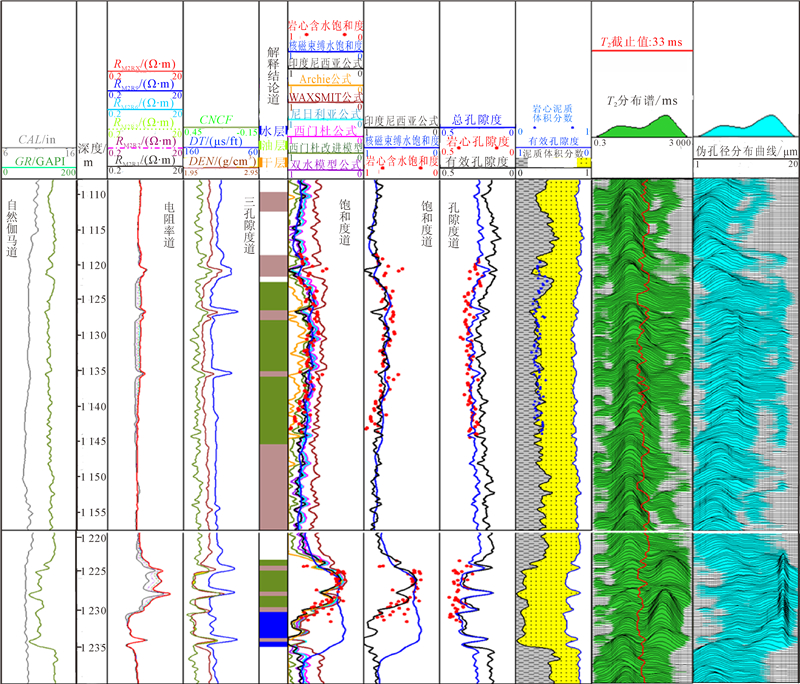 |
| 图 5 X2井低阻油层饱和度评价成果图 Fig. 5 Results figure of low resistivity reservoir saturation evaluation in well X2 |
| |
油层中的水均以束缚水的形式存在,因此利用核磁束缚水饱和度可以标定油层的含水饱和度。基于核磁共振[16, 17]计算束缚水饱和度(以33 ms为横向驰豫时间(T2)截止值)的公式如下:

由图 4、图 5左边第7道结果可见,在低阻油层段,核磁束缚水饱和度与印度尼西亚公式计算的含水饱和度以及校正后的岩心含水饱和度均比较一致,证实了岩心资料的标定是可靠的。在油水同层段,岩心校正后的含水饱和度与印度尼西亚公式计算的结果吻合最好,且核磁束缚水饱和度远小于计算的含水饱和度,表明此层含有大量可动水。在图 5中1 220~1 240 m岩性较纯的砂岩储层,各种饱和度模型计算的结果基本一致,相差不大,均与岩心含水饱和度吻合较好,结合核磁束缚水饱和度进行分析,本层上部为油层,下部为水层。由此可见,地层泥质含量的多少对不同饱和度模型的计算结果有着显著的影响。
以上7种饱和度模型在珠江口盆地低阻油层的适应性表明,相比密闭取心含水饱和度以及核磁束缚水饱和度,Archie和西门杜公式计算的含水饱和度明显偏高,尼日利亚、Waxman-Smits以及西门杜改进模型计算的结果则偏小,而双水模型和印度尼西亚公式计算的结果与之比较接近;相比较而言,印度尼西亚公式计算的结果最为吻合,因此也是最适合于本区泥质砂岩低阻油层的饱和度评价模型,与珠江口盆地适用于大部分区域的饱和度模型一致。同时,也证实了本区低阻油层的含水饱和度确实平均为70%~80%,且测试能够出油,具有一定的产能。 5 结论和建议
1)针对不同流体性质的储层,需要根据具体情况对密闭取心测量的饱和度进行脱气、覆压校正或油、水漏失的校正,在此基础上对测井计算的地层含水饱和度进行标定。 2)利用多种适用于泥质砂岩地层的饱和度模型进行计算,经过密闭取心饱和度标定和核磁束缚水饱和度的辅助验证,一方面,证实了本区低阻油层的含水饱和度;另一方面,确认了印度尼西亚公式是本区低阻油层饱和度评价最适合的模型。 3)岩心资料对于地层饱和度的评价是不可或缺的,尤其是在新探区或复杂地质条件下的储层,增加核磁共振测井,开展密闭取心作业,取全取准各项资料,通过对关键井的精细研究和认识,对整个区域低阻油层的测井评价都会有很大的指导作用。
| [1] | 田冷, 何顺利, 刘胜军, 等.广安地区须家河组气藏气水分布特征[J].天然气工业, 2009, 29(6):23-26. Tian Leng, He Shunli, Liu Shengjun, et al. Features of Gas and Water Distribution in the Xujiahe Formation Gas Reservoir of Guang'an Area[J]. Natural Gas Industry, 2009, 29(6):23-26. |
| [2] | 中国石油勘探与生产公司.低阻油气藏测井识别评价方法与技术[M].北京:石油工业出版社, 2006. China Petroleum Exploration and Production Company. Logging Identification and Evaluation Methods of the Low Resistivity Oil and Gas Reservoirs[M]. Beijing:Petroleum Industry Press, 2006. |
| [3] | 雍世和, 张超谟.测井数据处理与综合解释[M].东营:石油大学出版社, 1996. Yong Shihe, Zhang Chaomo. Log Data Processing and Integrated Interpretation[M]. Dongying:Petroleum University Press, 1996. |
| [4] | 李辉, 李伟忠, 张建林, 等. 正理庄油田低电阻率油层机理及识别方法研究[J]. 测井技术, 2006, 30(1):76-79. Li Hui, Li Weizhong, Zhang Jianlin, et al. The Mechanism and Identification Method of Low Resistivity Reservoir in Zhenglizhuang Oilfield[J]. Well Logging Technology, 2006, 30(1):76-79. |
| [5] | 杨春梅, 张吉昌.成因机理控制下的低电阻率油层发育特征及地质目标优选[J].吉林大学学报:地球科学版, 2009, 39(2):328-333. Yang Chunmei, Zhang Jichang. Characteristics and Origin of Low-Resistivity Reservoir Controlled by Petrophysics Mechanism and Geology Target Optimization[J]. Journal of Jilin University:Earth Science Edition, 2009, 39(2):328-333. |
| [6] | 辛治国, 侯加根, 冯伟光. 密闭取心饱和度校正数学模型[J]. 吉林大学学报:地球科学版, 2012, 42(3):698-704. Xin Zhiguo, Hou Jiagen, Feng Weiguang. Correction Model of Oil and Water Saturation in Sealing Core[J]. Journal of Jilin University:Earth Science Edition, 2012, 42(3):698-704. |
| [7] | 王艺景, 黄华, 刘志远, 等. 取心分析饱和度数理统计校正方法及其应用[J]. 江汉石油学院学报, 2000, 22(4):42-44. Wang Yijing, Huang Hua, Liu Zhiyuan, et al. Mathematically Statistical Calibration for Saturation Analysis by Coring and Its Application[J]. Journal of Jianghan Petroleum Institute, 2000, 22(4):42-44. |
| [8] | 刘丽. 基于物理模拟实验的密闭取心井油水饱和度校正[J].石油钻采工艺, 2009, 31(2):82-85. Liu Li. Oil and Water Saturation Correction for Sealed Coring Wells Based on Physical Simulation Experiments[J]. Oil Drilling & Production Technology, 2009, 31(2):82-85. |
| [9] | 欧阳健. 石油测井解释与储层描述[M].北京:石油工业出版社, 1994. Ouyang Jian. Petroleum Logging Interpretation and Reservoir Characterization[M]. Beijing:Petroleum Industry Press, 1994. |
| [10] | 顾保祥, 刘维永. 绥中36-1油田水淹层密闭取心饱和度校正[J]. 中国海上油气, 2008, 20(1):38-40. Gu Baoxiang, Liu Weiyong. Saturation Correction of Sealed Coring for Water-Flooded Zones in SZ36-1 Oilfield[J]. China Offshore Oil and Gas, 2008, 20(1):38-40. |
| [11] | 张斌成, 谢治国, 刘瑛, 等. 吐哈油田密闭取心岩样饱和度分析及校正方法[J]. 吐哈油气, 2005, 10(3):251-254. Zhang Bincheng, Xie Zhiguo, Liu Ying, et al. Saturation Analysis and Correct Method of Pressure Coring Sample in Tuha Oilfiled[J]. Tuha Oil & Gas, 2005, 10(3):251-254. |
| [12] | 宋延杰, 姜艳娇, 宋杨, 等.古龙南地区低阻油层胶结指数和饱和度指数影响因素实验[J].吉林大学学报:地球科学版, 2014, 44(2):704-714. Song Yanjie, Jiang Yanjiao, Song Yang, et al.Experimental Research on the Influencing Factors of m and n of Low Resistivity Oil Reservoirs in Southern Gulong Area[J].Journal of Jilin University:Earth Science Edition, 2014, 44(2):704-714. |
| [13] | 孙建国.阿尔奇(Archie)公式:提出背景与早期争论[J].地球物理学进展, 2007, 22(2):472-486. Sun Jianguo.Archie's Formula:Historical Background and Earlier Debates[J]. Progress in Geophysics, 2007, 22(2):472-486. |
| [14] | 柴婧, 王敏, 杨波. 基于印度尼西亚公式的饱和度改进模型[J]. 石油地质与工程, 2010, 24(2):75-78. Chai Jing, Wang Min, Yang Bo. Modified Saturation Model Based on the Indonesia Equation[J]. Petroleum Geology and Engineering, 2010, 24(2):75-78. |
| [15] | 姚军朋, 司马立强.合川地区低孔低渗砂岩储层含水饱和度的评价方法[J]. 天然气工业, 2010, 30(10):22-25. Yao Junpeng, Sima Liqiang. Evaluation Methods for Water Saturation of Low Porosity and Low Permeability Sandstone Reservoirs in the Hechuan Area[J]. Natural Gas Industry, 2010, 30(10):22-25. |
| [16] | Coates G R, Xiao Lizhi, Prammer M G. NMR Logging Principles & Applications[M]. Huston:Sea Gulf Press, 1999. |
| [17] | 马辉, 李瑞. 核磁共振测井在X 油田长8 储层流体识别中的应用[J]. 石油仪器, 2010, 25(3):54-58. Ma Hui, Li Rui. Application of Nuclear Magnetic Resonance Logging to Fluid Identification of Chang 8 Reservoir in X Oilfield[J]. Petroleum Instruments, 2010, 25(3):54-58. |