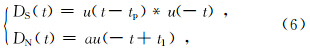2. 吉林大学仪器科学与电气工程学院, 长春 130026;
3. 吉林大学地球科学学院, 长春 130061
2. College of Instrument Science and Electrical Engineering, Jilin University, Changchun 130026, China;
3. College of Earth Sciences, Jilin University, Changchun 130061, China
0 引言
在地震勘探[1]生产中,同传统爆炸震源[2]相比,可控震源[3, 4, 5, 6, 7]由于具有安全、控制方便和作业效率高的优势,已成为目前地震勘探中重要的激发手段。
可控震源通过向地下长时间输入低能量扫频信号,利用相关检测技术将接收到的数据压缩为克劳德(Klauder)子波[8]形式的有效信号。因此,可控震源的原始地震记录存在两种记录形式:相关前的可控震源地震记录和相关后类似于爆炸震源记录的可控震源地震记录[9]。在实际地震勘探中,随机噪声始终伴随着地震数据的采集过程。在相同的噪声条件下,可控震源相关前记录和爆炸震源记录的随机噪声是一样的。爆炸震源所产生的子波信号能量强,随机噪声对其干扰的程度较弱,而且利用随机噪声的随机分布特点就可以极大改善爆炸震源地震记录的质量;而可控震源相关前记录中的信号为扫频信号,不能直接将爆炸震源的随机噪声压制方法[10, 11]应用到相关前记录中。通过相关检测[12, 13]可以将相关前记录转换为相关记录,但相关算子是非线性算子,在对可控震源相关前记录进行相关检测时,同时对其中的随机噪声进行了非线性运算,使得可控震源相关记录中的随机噪声发生了非线性变化;因此,不能利用爆炸震源的随机噪声压制方法。
当噪声较弱时,相关检测方法可以压制大部分随机噪声。当噪声较强或者存在一定量的强脉冲噪声时[14],相关检测方法不仅难以压制这些随机噪声和强脉冲噪声,还会引起可控震源相关记录的质量明显变差。对于直接采集相关记录的可控震源地震勘探而言,这些采集资料的质量难以保证。因此,可控震源中脉冲噪声的分析就显得尤为重要。
笔者通过数值模拟,系统分析脉冲噪声在相关处理前后的特点,并研究脉冲噪声对可控震源地震记录的干扰程度,为可控震源记录中脉冲噪声的检测及处理[15, 16]提供理论依据。 1 可控震源相关的检测原理及方法
可控震源勘探[17]通过向地下输入一个长时间的线性扫频地震波信号,在地下介质中传播后,利用采集系统进行长时间的记录。这种未经过相关的地震记录是可控震源最原始的地震记录(图 1)。
 |
| 图 1 可控震源工作(a)及相关检测(b)原理 Fig. 1 Vibrator system operational principle (a) and correlated detection method (b) |
| |
设u(t)为可控震源扫描信号:
式中:A为扫描信号振幅;f1和f2分别为扫描起始频率和终止频率;t为时间;T为扫描时间长度。
由于可控震源激发的地震波u(t)持续时间T远大于地下各反射界面之间的反射时差,相关前的各种信号都是以扫描信号u(t)的模式体现,不同的信号相互叠加以至于难以直接分辨有效信号的类型。但由于u(t)满足确定的函数关系式,通过将原始可控震源地震记录s(t)与扫描信号u(t)进行互相关,就可实现对信号的压缩(图 1),即
其中:D(t)为子波形式的地震记录; 为相关算子。
为相关算子。
对各向同性层状模型的地下介质而言,采集信号中通常包含多种有效信号,这里仅以单个反射波为例。在不考虑外界噪声干扰的情况下,检波器接收到的信号s(t)=u(t-tp),tp为反射波到时,则
2 脉冲噪声对可控震源地震记录的干扰在实际可控震源地震勘探中,地震记录中伴随的随机电脉冲、微震、强外源噪声等表现为持续时间短、相对地震信号幅度大的特点,根据脉冲噪声在地震记录中延续的采样点数可分为单点脉冲噪声和多点脉冲噪声,两种脉冲噪声随采样率的不同可互相转换。将脉冲持续长度为一个采样点的脉冲噪声定义为单点脉冲噪声。此外,单点脉冲噪声进行高采样率采样时,就转化为多点脉冲噪声,多点脉冲噪声又可以视为多个单点脉冲噪声的集合。在提取可控震源地震记录中的有效信号时,需要用到相关算子,加载到地震记录中的各种脉冲噪声经过非线性的相关运算后,产生了不可预期的变化。本文主要通过仿真实验,分析单点和多点脉冲噪声在相关检测后对有效信号的干扰。 2.1 单点脉冲
为了深入研究脉冲噪声在相关前后对可控震源地震记录的影响,本文先以单点脉冲为例进行分析。设n(t)为幅度为1、到时为0 s的单点脉冲,即 ,则幅度为a1、到时为t1时刻的单点脉冲噪声表示为N(t)=a1n(t-t1)。将脉冲噪声强度a定义为N(t)的幅度与s(t)的振幅比,它反映了单点脉冲噪声相对于信号的噪声强度。下文中将仿真的数据s(t)的振幅定为1,则a=a1。
,则幅度为a1、到时为t1时刻的单点脉冲噪声表示为N(t)=a1n(t-t1)。将脉冲噪声强度a定义为N(t)的幅度与s(t)的振幅比,它反映了单点脉冲噪声相对于信号的噪声强度。下文中将仿真的数据s(t)的振幅定为1,则a=a1。
令S(t)为含单点脉冲噪声的可控震源地震记录,则
以可控震源扫描信号u(t)为相关参考信号,S(t)经相关处理即得相关域数据D(t):
式中,*为卷积算子。令
则
由式(7)可以看出,数据D(t)由两部分组成:DS(t)是有效反射波;DN(t)是脉冲噪声N(t)引起的干扰,其特点是将参考信号u(t)翻转移位t1时间,干扰振幅放大a倍,因而引起的干扰范围扩大。可控震源数据的相关过程使得数据存在正向数据和负向数据,正向数据是所需的有效数据[18]。由公式(6)可知:当t1≤T时,干扰范围为0~t1;当t1>T时,干扰范围为(t1-T)~t1。
令u(t)中的A=1,f1=10 Hz,f2=100 Hz,T=5 s,采样间隔为1 ms,由公式(1)得到震源的线性升频控制信号如图 2a所示;图 2b为t1=2.5 s、a=1的单点脉冲;图 2c为图 2a中的线性升频控制信号与图 2b中的脉冲信号的相关结果;图 2d和图 2e分别为图 2a和图 2c的时频图。对比图 2a和图 2c以及图 2d和图 2e可以明显看出,单点脉冲信号在相关后引起的干扰实际上相当于将参考信号反转移位后的结果。定义频率的变化梯度[19]G=(f2-f1)/T,则u(t)的频率变化梯度为18 Hz/s。因此,单点脉冲干扰后的频率变化梯度为-18 Hz/s。由公式(6)可知,DN(t)的截止频率等于u(t)的初始频率f1,其对应的时刻为单点脉冲所在时刻,因此可以计算图 2c中0~2.5 s内任意点的噪声频率,0 s处的频率为65 Hz。噪声的干扰范围由单点扩大为0~2.5 s。
 |
| a. 线性升频(10~100 Hz)chirp信号;b. 单点脉冲信号;c. chirp信号与单点脉冲信号相关结果;d. a图信号时频图;e.c图信号时频图。图 2 单点脉冲噪声在相关域中的干扰 Fig. 2 Interference of one-point pulse in the correlated field |
| |
下面从单点脉冲的强度a和出现时刻t1来定量分析这种干扰程度。
设可控震源扫描信号振幅为A,时间长度为T,采样间隔为ts,由相关运算可得有效信号的最大幅度为Amax=AT/(2ts),则单点脉冲对可控震源相关后的记录信号完全覆盖的最小幅度即为Amax。
采用上述u(t)参数,令a=0、500、1 000、1 500、2 000、2 500,tp=1 s,t1=2.5 s,ts=1 ms,T=5 s。此时Amax=2 500,得到相关域单道数据模拟结果如图 3所示。
在本文中,笔者选取时窗长度为0.04 s,采用能量叠加法[20]求取信噪比:

式中:ES为信号功率;EN为噪声功率。
从图 3和表 1中可以看出,不同脉冲噪声强度的单点脉冲对相关后的有效信号干扰程度不同,脉冲噪声强度越大,干扰有效信号的程度就越强。由表 1可以直观地看出:当a为1 500时,单点脉冲已经对有效信号产生了较强的干扰,信噪比为-1.42 dB;当a为2 500时,有效信号几乎被噪声淹没,信噪比降低至-5.89 dB。由此可见,当单点脉冲的强度a大于Amax的60%时,有效信号就会受到较强的干扰,以至于难以提取到有效信号。
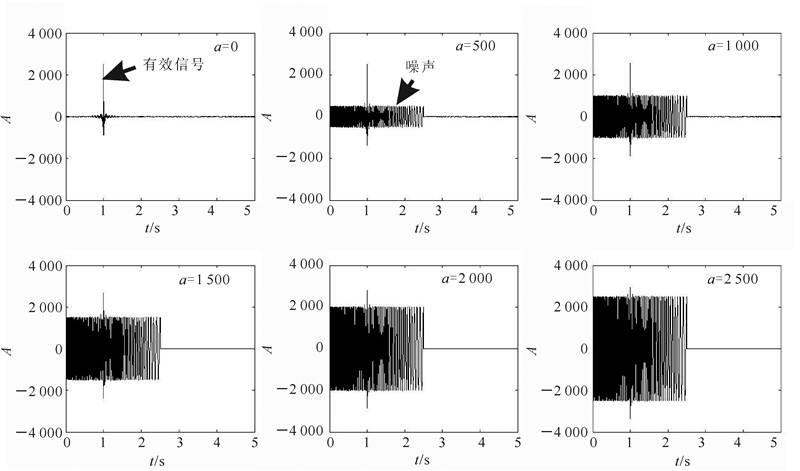 |
| 图 3 单点脉冲噪声强度a对相关后数据干扰 Fig. 3 Interference with the amplitude of one-point pulse inference in the correlated data |
| |
| a | SNR/dB | (a/Amax)/% |
| 0 | 不受噪声干扰 | 0 |
| 500 | 8.33 | 20 |
| 1 000 | 2.16 | 40 |
| 1 500 | -1.42 | 60 |
| 2 000 | -3.94 | 80 |
| 2 500 | -5.89 | 100 |
脉冲噪声对可控震源地震数据的干扰不仅与a有关,还与t1有关。令a=1 500,tp=1 s,t1分别等于0.5、1.5、2.5、3.5、4.5、5、5.5、6.0 s,单点脉冲噪声的时间位置对相关域数据的干扰如图 4所示。
图 4直观地反映了DN(t)随t1的变化:当t1≤T时,单点脉冲噪声对可控震源地震数据的干扰时间长度随t1的增加而线性增加,受到单点脉冲干扰的时间范围为0~ t1;当t1>T时,单点脉冲噪声对可控震源地震数据的干扰时间长度不变,为(t1-T)~t1。表 2为受不同t1的单点脉冲干扰后的信噪比。图 4和表 2表明不同到时的单点脉冲对信号的干扰程度不同:当tp>t1或者tp<(t1-T)时,单点脉冲对信号几乎没有干扰;当信号的到时t1<tp<(t1-T)时,单点脉冲对信号的干扰程度基本不变。
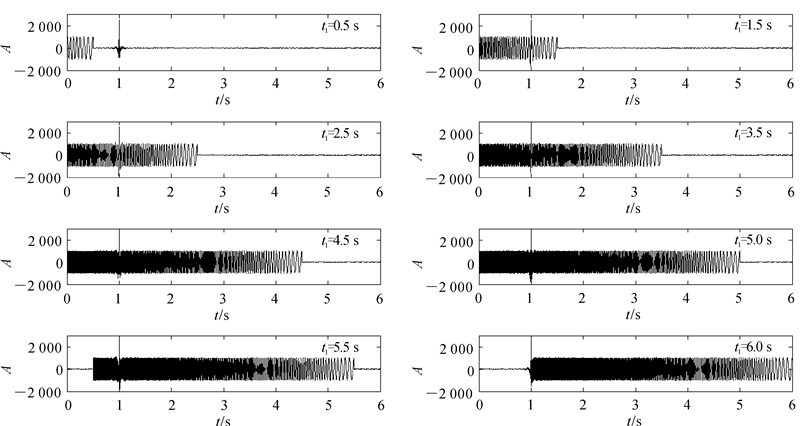 |
| 图 4 单点脉冲噪声的时间位置对相关域数据的干扰 Fig. 4 Interference of the one-point pulse’s time position in the correlated data |
| |
| t1/s | SNR/dB | 干扰范围/s |
| 0.5 | 不受噪声干扰 | 0~0.5 |
| 1.5 | 1.22 | 0~1.5 |
| 2.5 | 2.16 | 0~2.5 |
| 3.5 | 2.18 | 0~3.5 |
| 4.5 | 2.04 | 0~4.5 |
| 5.0 | 1.94 | 0~5.0 |
| 5.5 | 2.10 | 0.5~5.5 |
| 6.0 | 2.25 | 1.0~6.0 |
实际数据的脉冲噪声经常表现为一个或者多个具有一定延续度的多个单点脉冲噪声的集合,即多点脉冲噪声。下面从理论上分析多点脉冲对可控震源地震记录的干扰。
由多点脉冲噪声定义,多点脉冲噪声可表示为
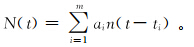
式中:m为多点脉冲采样点数;ti为多点脉冲第i点处脉冲出现的时刻(ti<ti+1);ai为ti处的脉冲强度。则
以震源控制信号为相关参考道,S(t)经相关处理即得相关域数据D(t):
则
对比公式(6)和公式(10)可知,多点脉冲对可控震源地震记录的干扰DNp(t)实际上是多个单点脉冲对可控震源地震记录的干扰DN(t)的线性叠加。
图 5是仿真多点脉冲噪声对可控震源数据在相关域中引起的干扰。图 5a为1个多点脉冲,ts=0.001 s,m=11,ti=3+(i-6)ts,i=1,2,… ,11。图 5b为参考信号与图 5a中的多点脉冲相关结果。图 5c为2个多点脉冲,ts=0.001 s,m=22, 。图 5d为参考信号与图 5c中多点脉冲的相关结果。相邻的11个单点脉冲的强度变化为余弦形式,即ai=cos(π/10(i-6)),i=1,2,… ,11。对比图 5c、图 5b和图 5d,可以明显看出多点脉冲信号产生的干扰更为复杂,干扰范围由脉冲的最远时刻确定,局部干扰强度增强。
。图 5d为参考信号与图 5c中多点脉冲的相关结果。相邻的11个单点脉冲的强度变化为余弦形式,即ai=cos(π/10(i-6)),i=1,2,… ,11。对比图 5c、图 5b和图 5d,可以明显看出多点脉冲信号产生的干扰更为复杂,干扰范围由脉冲的最远时刻确定,局部干扰强度增强。
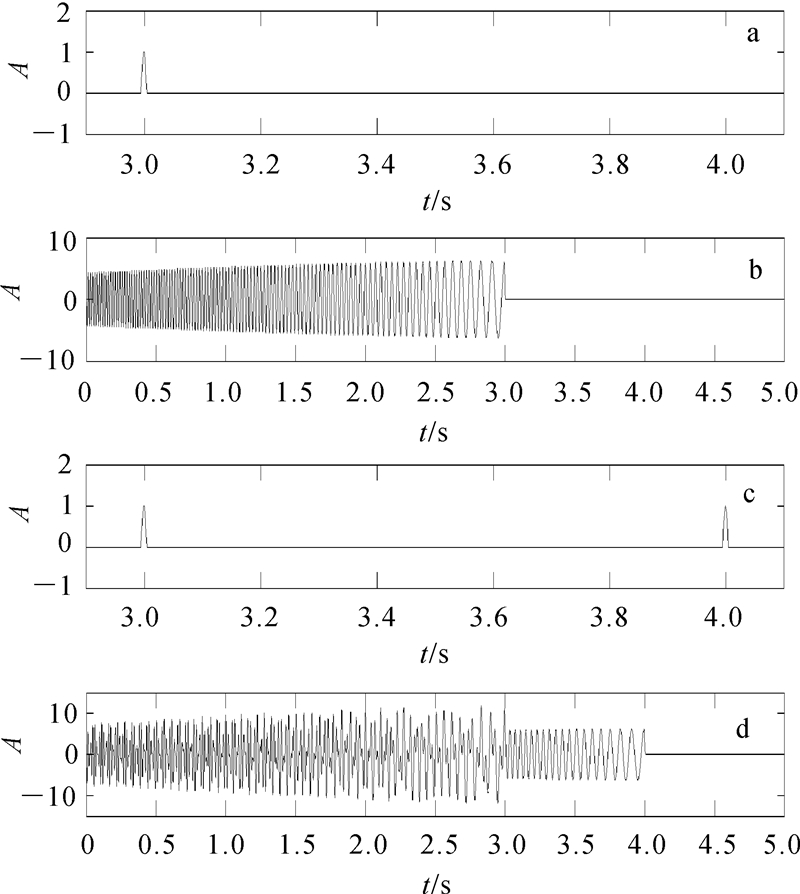 |
| a. 1个10点脉冲信号(3 s处);b. 参考信号与1个多点脉冲信号相关;c. 2个10点脉冲信号(3 s和4 s处);d. 参考信号与2个多点脉冲信号相关。 图 5 单点脉冲噪声的时间位置对相关域数据的干扰 Fig. 5 Interference of multi-point pulse noise in the correlated field |
| |
为了能够深入分析多点脉冲的干扰情况,定义多点脉冲噪声点数比例为q= ,其中,n为非相关记录的采样点数;平均强度为a=
,其中,n为非相关记录的采样点数;平均强度为a= 。则根据公式(1)和公式(9)得
。则根据公式(1)和公式(9)得
对比公式(6)、公式(10)和公式(11)可知,采样点数为nq、平均强度为a的脉冲噪声对相关后0~t1时间内数据的干扰程度最大可以达到脉冲强度为a的单点脉冲噪声对相关后结果干扰的nq倍。
考虑更符合实际的情况,根据系统和环境噪声是随机的,且服从正态分布[21],构造时间位置和噪声强度都服从正态分布的随机脉冲噪声,相关检测结果如图 6所示。
 |
| 图 6 脉冲平均强度为100时不同脉冲点数比例的相关叠加结果 Fig. 6 Correlation results with different point scales when a=100 |
| |
图 6中的相关参考信号为震源激发信号,表 3为图 6信噪比数据。由图 6可以直观看出,相关检测后噪声的平均强度和干扰程度,总体上随q增加而加强。当a≥100、脉冲噪声比例超过记录点数的2.5%时,SNR小于0,信号淹没于噪声中。为了更准确地分析q的干扰情况,针对上述仿真数据,可以得到相关后信噪比随脉冲噪声点数比例q变化曲线(图 7)。由图 7可以看到,脉冲噪声在相关域的干扰导致SNR随q的增加整体上先降低而后升高,在1.92%<q<96.03%的较大范围内,信噪比都小于0,信号已完全被噪声淹没,难以分离有效信号。下面分析多点脉冲的a对相关后结果的干扰程度。令q=1.5%,a=0、10、50、100、200、400、600、800和1 000,其相关检测结果如图 8所示。表 4为图 8中不同脉冲平均强度的信噪比数据。
| q/% | SNR/dB |
| 0.17 | 14.87 |
| 0.67 | 8.91 |
| 1.50 | 2.41 |
| 2.50 | -1.70 |
| 6.67 | -2.85 |
| 11.66 | -4.29 |
| 20.00 | -5.56 |
| 33.33 | -10.91 |
| 49.99 | -9.90 |
| 66.66 | -6.02 |
| 83.32 | -3.74 |
 |
| 图 7 信噪比随脉冲噪声点数比例的变化 Fig. 7 Signal-to-noise ratio with different point scales |
| |
| a | SNR/dB |
| 10 | 22.89 |
| 50 | 8.91 |
| 100 | 2.88 |
| 200 | -3.13 |
| 400 | -9.15 |
| 600 | -12.67 |
| 800 | -15.17 |
| 1 000 | -17.11 |
由图 8和图 3可以看出:多点脉冲噪声在相关域引起的噪声干扰和单点脉冲噪声引起干扰的现象一样,a愈大,引起的干扰愈强;当脉冲噪声的比例达到记录的1.5%、脉冲平均强度a超过200时,SNR小于0,有效信号被噪声淹没。
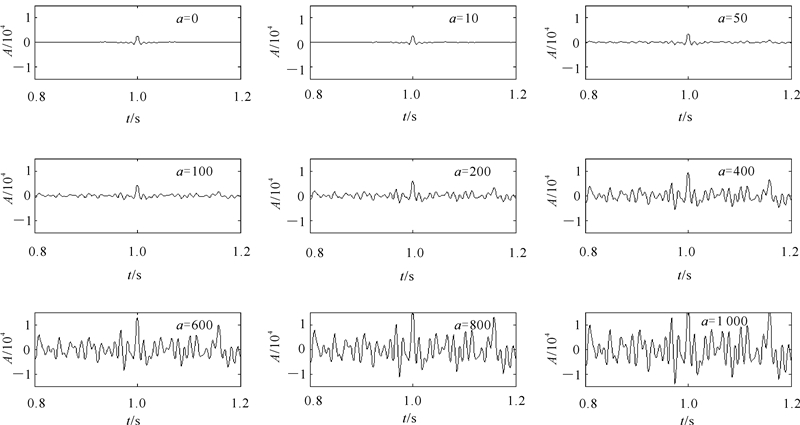 |
| 图 8 q=1.5%时不同的脉冲平均强度相关叠加结果 Fig. 8 Correlation results with different mean intensities when q=1.5% |
| |
同时,为了准确分析脉冲平均强度的干扰程度,针对图 8数据计算得到信噪比随脉冲平均强度的变化曲线(图 9)。由图 9可得:在多脉冲噪声的干扰下,可控震源相关记录的SNR随a的增加单调减小。整个曲线先快速减小,而后缓慢变化,说明平均强度对信噪比的干扰由强变弱;SNR约为0时对应的a为132,当a大于132时,SNR小于0,信号完全被噪声淹没。
 |
| 图 9 信噪比随平均强度的变化曲线 Fig. 9 Signal-to-noise ratio with different mean intensities |
| |
通过上述研究,可以得到以下认识:
1)相关检测方法不仅难以压制可控震源非相关域记录中的脉冲噪声,而且将脉冲噪声的干扰程度扩大化。
2)可控震源非相关域记录的脉冲噪声对可控震源相关记录的干扰程度主要与脉冲噪声强度、所在时间位置以及可控震源非相关记录脉冲点数比例三方面因素有关。
因此,无论在野外进行可控震源数据采集还是对可控震源数据进行相关处理时,都应该首先进行脉冲噪声控制或压制,减弱随机脉冲噪声对有效信号的干扰,以保证良好的可控震源数据质量。
| [1] | 何樵登.地震勘探原理和方法[M].北京:地质出版社,1986. He Qiaodeng. Principle and Method of Seismic[M]. Beijing:Geological Publishing House,1986. |
| [2] | 张智,刘财,邵志刚.地震勘探中的炸药震源药量理论与实验分析[J].地球物理学进展,2003,18(4):724-728. Zhang Zhi,Liu Cai,Shao Zhigang. Theory and Experimentation of the Charge Sizes in Seismic Sources for Seismic Exploration[J]. Progress in Geophysics,2003,18(4):724-728. |
| [3] | 佟训乾,林君,姜弢,等.陆地可控震源发展综述[J].地球物理学进展,2012,27(5):1912-1921. Tong Xunqian,Lin Jun,Jiang Tao,et al. Summary of Development of Land Vibrator[J]. Progress in Geophysics,2012,27(5):1912-1921. |
| [4] | 王忠仁,刘瑞,陈卫,等.可控震源的互补组合激发技术[J].吉林大学学报:地球科学版,2013,43(6):2044-2049. Wang Zhongren,Liu Rui,Chen Wei,et al. The Complementary Combination Stimulating Technology for Controllable Seismic Source[J]. Journal of Jilin University:Earth Science Edition,2013,43(6):2044-2049. |
| [5] | 王俊秋,林君,姜弢,等.可控震源地震方法在金昌铜镍矿区的应用实验[J].吉林大学学报:地球科学版,2011,41(5):1617-1622. Wang Junqiu,Lin Jun,Jiang Tao,et al. Experiment and Application of Controlled Vibrator Seismic Method at Jinchang Copper-Nickel Metal Deposit[J]. Journal of Jilin University:Earth Science Edition,2011,41(5):1617-1622. |
| [6] | 王忠仁,陈祖斌,姜弢,等.可控震源地震勘探的数值模拟[J].吉林大学学报:地球科学版,2006,36(4):627-630. Wang Zhongren,Chen Zubin,Jiang Tao,et al. Numerical Simulation for Seismic Exploration with Vibrator[J]. Journal of Jilin University:Earth Science Edition,2006,36(4):627-630. |
| [7] | 王俊秋,林君,陈祖斌,等.小型可控震源在油页岩地震勘探中的应用试验[J].吉林大学学报:地球科学版,2012,42(3):265-270. Wang Junqiu,Lin Jun,Chen Zubin,et al. Experiment and Application of Mini-Vibrators Seismic Exploration in Oil Shale[J]. Journal of Jilin University:Earth Science Edition,2012,42(3):265-270. |
| [8] | Li Xiaoping,Hubral P. Harmonic Distortion in Vibroseis Data and Its Elimination[J]. SEG Expanded Abstracts,1995,14(1):1010-1013. |
| [9] | Shuang Qin,David K S. Filtering Vibroseis Data in the Precorrelation Domain[J]. Geophysical Prospecting,1998,46(3):303-322. |
| [10] | 林红波,李月,徐学纯.压制地震勘探随机噪声的分段时频峰值滤波方法[J]. 地球物理学报,2011,54(5):1358-1366. Lin Hongbo,Li Yue,Xu Xuechun. Segmenting Time-Frequency Peak Filtering Method to Attenuation of Seismic Random Noise[J]. Chinese Journal of Geophysics,2011,54(5):1358-1366. |
| [11] | 李月,林红波,杨宝俊,等.强随机噪声条件下时窗类型局部线性化对TFPF技术的影响[J].地球物理学报,2009,52(7):1899-1906. Li Yue,Lin Hongbo,Yang Baojun,et al. The Influence of Time Window on TFPF Under the Strong Noise Background[J]. Chinese Journal of Geophysics,2009,52(7):1899-1906. |
| [12] | 槐永军,武永生.可控震源的相关技术[J].物探装备,2009,19(1):30-32. Huai Yongjun,Wu Yongsheng. Correlation Technique of Vibroseis[J]. Equipment for Geophysical Prospecting,2009,19(1):30-32. |
| [13] | 姜弢,林君,陈祖斌,等.可控震源相控地震的相关检测技术[J].仪器仪表学报,2005,26(4):336-339. Jiang Tao,Lin Jun,Chen Zubin,et al. The Correlation Detection Method of Signals in Phased Array of Vibroseis System[J]. Chinese Journal of Scientific Instrument,2005,26(4):336-339. |
| [14] | 魏铁,于世东,于敏杰,等.可控震源噪声分析[J].石油地球物理勘探,2008,43(增刊2):38-43. Wei Tie,Yu Shidong,Yu Minjie,et al. Analysis of Noise in Vibroseis[J]. Oil Geophysical Prospecting,2008,43(Sup.2):38-43. |
| [15] | Kneib G,Leykam A. Debursting of Uncorrelated Vibroseis Data[J]. First Break,1999,17(8):283-287. |
| [16] | 涂国田.一种检测抑制地震记录猝发噪声的方法[J].物探化探计算技术,1993,15(4):316-320. Tu Guotian. Method of Predicting and Liminating Pulse Noise in Seismic Data[J].Computing Techniques for Geophysical and Geochemical Exploration,1993,15(4):316-320. |
| [17] | 林君.电磁驱动可控震源地震勘探原理及应用[M].北京:科学出版社,2004. Lin Jun. Seismic Exploration and Application of Vibrator Driven by Electromagnetic[M]. Beijing:Science Press,2004. |
| [18] | 物探局研究所震源室.可控震源的原理及工作方法[J].石油地球物理勘探,1977(4):1-34. Source Chamber,Institute of Geophysical Prospecting Bureau. Theroy of Vibroseis and Working Method[J]. Oil Geophysical Prospecting,1977(4):1-34. |
| [19] | Polom Ulrich. Elimination of Noise Caused by Spikes and Bursts in Vibroseis Data[J].Pure Applied Geophysics,1999,156(1/2):319-344. |
| [20] | 张军华.地震资料去噪方法:原理、算法、编程及应用[M].东营:中国石油大学出版社,2008. Zhang Junhua. Seismic Data Denoising Method Theory,Algorithm,Programming and Application[M]. Dongying:China University of Petroleum Press,2008. |
| [21] | 冯霞,龚晓峰,张利丹,等.基于纹理特征的背景噪声提取的应用研究[J].电子学报,2009,37(9):2092-2095. Feng Xia,Gong Xiaofeng,Zhang Lidan,et al. Research of Background Noise Extraction Based on Texture Feature[J]. Acta Electronica Sinica,2009,37(9):2092-2095. |