2. 中国石油吉林油田公司地球物理勘探研究院, 吉林 松原 138000
2. Research Institute of Geophysical Prospecting, Jilin Oilfield Company, CNPC, Songyuan 138000, Jilin, China
0 引言
小波去噪是一类有效分离信号与随机噪声的方法。在地震随机噪声消除中:张波等[1]利用小波分析和反演方法联合去除随机噪声;王典等[2]基于提升算法和百分位数软阈值消除地震随机噪声,并取得明显的效果;樊计昌等[3]提出了小波包节点域和空间域倾角扫描高阶相关去噪技术;Zhang等[4]基于非线性小波阈值去噪和递归最优阈值除去地震随机噪声,保持了处理信号的平滑度和完整性;王志强等[5]利用检波器组合响应来提高地震资料的信噪比,压制随机噪声。然而,小波变换对非平稳信号的表征存在很大的局限性。
类小波变换在地震图像处理和数据分析中具有很广泛的应用[6,7,8],其主要利用数据的方向特性[9,10,11]。Fomel等[12,13]开发了一种针对地震数据方向性的数学变换方法,命名为“Seislet变换”,Seislet变换的定义结合了小波提升算法和局部平面波分解技术。一般来说,沿测线方向的离散小波变换是一种特殊的零倾角Seislet变换,Seislet变换能够更有效地压缩地震数据[14]。其中,局部地震倾角的求取是该方法的核心。局部倾角的计算有多种方法。相干分析中的归一化互相干、任意多道相干、三维地震数据体相干算法都可以用来计算地震同相轴的局部倾角[15]。平面波分解滤波器(PWD)是一种特殊的预测误差滤波器,通过局部平面波方程的表征,使分解残差达到最小来确定局部倾角[16]。也可以通过希尔伯特变换用瞬时空间频率与瞬时时间频率的比值来获取局部倾角[17]。利用曲波变换在曲波域可以实现同时对多个倾角的估计[18]。然而,在低信噪比的条件下,上述方法存在一些局限。
Donoho等[19]于1994年提出了信号去噪的软阈值方法和硬阈值方法,这种方法广泛应用于各个领域。然而,硬阈值函数不连续,软阈值函数不可导。为了克服硬阈值函数和软阈值函数的缺点,很多学者对这一问题进行了研究。Gao等[20]提出了半软阈值方法进行改进;李冲泥等[21]于1999年提出一种新的阈值函数,该函数连续可导,弥补了原函数的分段性和不连续性;许丽群[22]于2010年提出了软硬阈值折中法,既克服了硬阈值函数不连续的缺点,同时又克服了软阈值函数中估计小波系数与分解小波系数之间存在着恒定偏差的缺陷。
在本次研究中,笔者从共中心点道集的反射时距曲线出发,建立了一种基于地震波运动方程且适应于低信噪比条件下倾角求取的方法,并将求出的局部地震倾角用于构建新型Seislet变换,将语音信号中改进的阈值方法引入地震数据处理中,通过理论模型和实际数据的处理结果验证本次研究方法的有效性。 1 理论基础 1.1 基于时距关系地震倾角的新型Seislet变换
Seislet变换是把小波提升算法同局部平面波分解技术相结合(见附录A),改进了小波提升算法中的预测算子P(公式(A-4))和更新算子U(公式(A-7)),使之能够沿着同相轴的方向进行预测和更新。

以往Seislet变换在低信噪比的条件下存在着一些局限。在本文中,笔者从共中心点道集中地震倾角的定义出发,提出一种适应于低信噪比条件下的倾角求取方法,并用于定义新型Seislet变换。经典反射波双曲时距关系[24]为


由倾角的公式(公式(4))可以看出,如果能够求出对应于每一点(t,x)的速度vn(t0,x),就能得到随炮检距x和时间t而逐渐变化的倾角。在共中心点道集中,速度扫描是一种能够在低信噪比条件下稳定求取均方根速度的方法,利用得到的扫描速度,根据公式(4)能够准确地计算出地震局部倾角。
由于经典反射波双曲时距关系是在水平界面和近炮检距假设基础上提出的,因此通过公式(4)计算的同相轴倾角也需要满足这2个条件。在不同地层产状的地震模型下,只要满足该假设条件,本方法能够得到准确的时空变化倾角,在低信噪比条件下也具有较好的适应性。对于大炮检距和各向异性所引起的非双曲反射同相轴,可以选取非双曲时距曲线方程[25]进行推导,此时将会增加额外参数,多参数扫描方法能够提供稳定的求解方案。 1.2 阈值去噪
阈值去噪是一种应用稀疏变换进行信噪分离的方法。信号在变换域内能量主要集中在有限的几个系数中,而噪声的能量分布于整个变换域内,因此,经稀疏变换后,信号的变换系数幅值大于噪声的变换系数幅值。如果找到一个合适的阈值,当变换系数小于该阈值时,认为这时的系数主要是由噪声引起的,当变换系数大于该阈值时,则认为其主要是由信号引起的;当对变换系数进行阈值处理后,反变换就可以达到去除噪声而保留有用信号的目的。
1.2.1 硬阈值与软阈值
硬阈值处理是把信号稀疏变换系数的绝对值与阈值比较,小于阈值的变换系数变为0,大于阈值的变换系数不变,再根据反稀疏变换进行信号重建,如图 1a所示。
软阈值处理是把稀疏变换系数中大于阈值的变为该值与阈值的差值,如图 1b所示。
硬阈值与软阈值函数的优缺点比较如表 1所示。
本文引入语音信号中改进的新阈值函数[26]:
为了验证本文提出的局部地震倾角的有效性,将基于时距关系和平面波分解滤波器计算出的局部地震倾角进行比较。首先建立一个经典的反射波双曲时距关系模型(图 2a),道间距为20 m,共128道。图 2b是无噪声条件下用平面波分解滤波器计算出的倾角。可以看出,平面波分解滤波器在高信噪比条件下能够获得准确的倾角。
接下来,在图 2a的模型中加入随机噪声,使得信噪比(SNR)为-8.20 dB(图 2c)。一般认为,信号能量与噪声能量之比大于3∶1,即SNR>4.77 dB时为高信噪比;相反,信号能量与噪声能量之比小于3∶1,即SNR<4.77 dB时为低信噪比。图 2d是低信噪比条件下用平面波分解滤波器计算出的倾角。此时,噪声对于平面波分解滤波器产生较大的影响,倾角值有很大的畸变。
对含噪模型(图 2c)进行速度分析,结果如图 3a所示。可以看出:在共中心点道集中,速度扫描能够在低信噪比条件下稳定求取均方根速度。图 3b为基于时距关系求得的地震局部倾角。
将求得的倾角(图 2d和图 3b)分别用于Seislet变换,得到2种情况的变换域系数(图 3c和图 3d)。对比两图可以看出:双曲型反射同相轴都得到了较好的压缩;但是PWD对应的变换域系数相比基于时距关系的变换域系数更加集中在小尺度范围内。这主要是因为,图 3c是由图 2c中的信号与随机噪声同时沿图 2d中畸变的倾角进行了压缩而得到的,而图 3d是由图 2c中的信号沿图 3b中准确的倾角进行压缩、随机噪声无法沿图 3b中准确的倾角进行压缩而得到的。
2.2 阈值去噪
首先选取在尺度方向的简单阈值方法,即将基于PWD和时距曲线关系的Seislet变换域中尺度大于5的Seislet变换系数置零(图 4a,b),然后做Seislet反变换得到去噪结果,如图 4c和图 4d所示。可以看到:基于PWD的Seislet反变换去噪结果同相轴产生较大的扭曲,基于时距曲线关系的Seislet反变换去噪结果比较合理;但是2幅图都含有一定程度的噪声,考虑用改进的阈值去噪方法对图像进行改进。
接下来,将改进的阈值方法引入基于时距关系的Seislet变换域中。首先由Donoho-Johnstone[27]提出的阈值确定模型t=
在实际数据处理中,使用墨西哥湾某海洋数据[28]来评估新方法的去噪效果。如图 6a所示,在时间-共中心点-炮检距域中,左下角剖面代表炮检距为0.134 km的共中心点道集,右下角剖面表示共中心点为11.892 km的共炮检距剖面,左上角剖面代表双程旅行时为2 s的时间切片。由速度分析(图 6b)的结果可以看出:该数据体层间多次波影响较小,速度谱中能量团比较集中。图 6c为提取的均方根速度,可以看出,该区域速度场比较平稳。图 6d为基于时距关系求得的局部地震倾角。将此倾角用于Seislet变换,如图 7a所示,反射信息主要集中在很小的尺度范围内,噪声却分布在整个变换域内。通过阈值估计模型得到阈值λ=1 251 348.25。然后用改进的阈值方法对基于时距关系的Seislet变换域系数做处理,Seislet反变换得到的去噪结果如图 7b所示。可以看出:改进的阈值方法去除了大部分随机噪声,提高了信噪比。
本文介绍了一种基于共中心点道集反射波时距关系的倾角计算方法,通过与平面波分解滤波器计算出的局部地震倾角对比,该方法能够求取出更适合低信噪比条件下的倾角,将这种倾角与Seislet变换框架结合,能够获得适用于低信噪比条件下的改进型Seislet变换方法。引入语音信号中改进阈值方法并与传统的硬阈值以及软阈值方法进行对比,理论模型的处理结果和去噪效果衡量指标证明这种改进的阈值方法不但适于地震信号,而且在提高信噪比方面优于传统阈值方法,是一种更加适合低信噪比条件下Seislet的变换阈值去噪方法。通过对实际数据的处理,验证了本文方法的正确性和优越性。
附录A 小波变换提升算法
提升算法的基本思想在于通过一个基本小波,逐步构建出一个具有更加良好性质的新的小波。一个规范的提升算法有3个步骤:分解、预测、更新。
1)将数据e0分解成为2个小的子集e-1和r-1。假定相邻的数据间有最大的相关性(在实际中也往往是这种情况),按照数据的奇偶序号对数据列进行间隔采样:
2)设一个与数据无关的预测函数P,可以用r-1和e-1的预测值之间的差值来代替r-1。如果使用合理的预测,那么差值将包含比原来r-1少得多的信息,产生的小波系数r-1中保留的是原信号的高频分量,也即信号中的随机信息分量。记
例如最简单的预测算子使用偶数序列中2个相邻数的均值作为它们之间奇数序列的预测值:
3)预测出原信号中的高频分量后,还需要求出信号中的低频分量,也即信号中的相关信息分量。通过设计更新算子U对e-1更新,就可以求出表示低频分量的小波变换尺度系数:
尺度系数的一个关键特性是它与原信号具有一样的平均值S,即S=
此时,已经可以用较小的数据序列e-1和小波系数r-1来代替原始的数据。如果有一个好的预测,那么2个子集{e-1,r-1}将产生比原来的序列e0更为紧凑的表示。接下来对这个算法进行周期重复。将e-1抽取成两个序列e-2和r-2,然后用r-2和r-2预测值之间的差值来代替r-2,用r-2对e-2进行更新,可以用小波表示{e-2,r-2,r-1}取代e0。这样经过n步,就可以用小波表示{e-n,r-n,…,r-1}来取代原来的数据序列。假使小波系数是由基于某种相关性的预测模型得到的,那么,{e-n,r-n,…,r-1}将给出一个比原序列更为紧凑的表示。然而,地震数据空间方向的数据分布特点并不满足小波变换的假设。


a. 硬阈值方法;b. 软阈值方法;c, d. 改进的阈值方法。图 1 不同阈值方法比较 Fig. 1 Fig.1 Comparison of different threshold methods 
优点 缺点
硬阈值
函数能够恢复
原始信号
的形态1.处理过的变换域系数w在±λ处是不连续的。
2.大于阈值的变换域系数中也存在噪声信号的干扰,对大于阈值的变换域系数不加处理。
3.将小于阈值的变换域系数直接设为0,这样很有可能将有用信号作为噪声滤除掉。
软阈值
函数阈值函数
连续去噪
效果比较
平滑1.阈值函数不可导。
2.当|d|≥λ时,w与d之间总存在恒定的偏差,这与噪声分量是随着小波系数增大而逐渐减小的趋势不相符。
3.将小于阈值的变换域系数直接设为0,这样很有可能将有用信号作为噪声滤除掉。

a. 理论模型;b. 图2a的倾角;c. 低信噪比模型;d. 图2c的倾角。p为慢度。图 2 不同信噪比条件下平面波分解滤波器求得的倾角比较 Fig. 2 Comparison of slopes of PWD method with different SNR 
a. 速度谱;b. 基于时距关系的局部地震倾角;c. 基于PWD的Seislet变换系数;d. 基于时距关系的Seislet变换系数。图 3 低信噪比模型不同方法变换系数比较 Fig. 3 Comparison of transform coefficients of different methods with low SNR 
a. 置零后基于PWD的Seislet变换系数;b. 置零后基于时距关系的Seislet变换系数;c. 基于PWD的Seislet去噪结果;d. 基于时距关系的Seislet去噪结果。图 4 低信噪比模型不同倾角的Seislet反变换效果比较 Fig. 4 Comparison of inverse Seislet transform of different slopes with low SNR  估计阈值(其中:n为小波系数的个数;σ为小波域内的噪声方差),得到t=0.44。用3种阈值方法对Seislet变换域系数做处理,然后Seislet反变换得到的结果如图 5所示。并用信噪比衡量处理的效果,如表 2所示。
估计阈值(其中:n为小波系数的个数;σ为小波域内的噪声方差),得到t=0.44。用3种阈值方法对Seislet变换域系数做处理,然后Seislet反变换得到的结果如图 5所示。并用信噪比衡量处理的效果,如表 2所示。
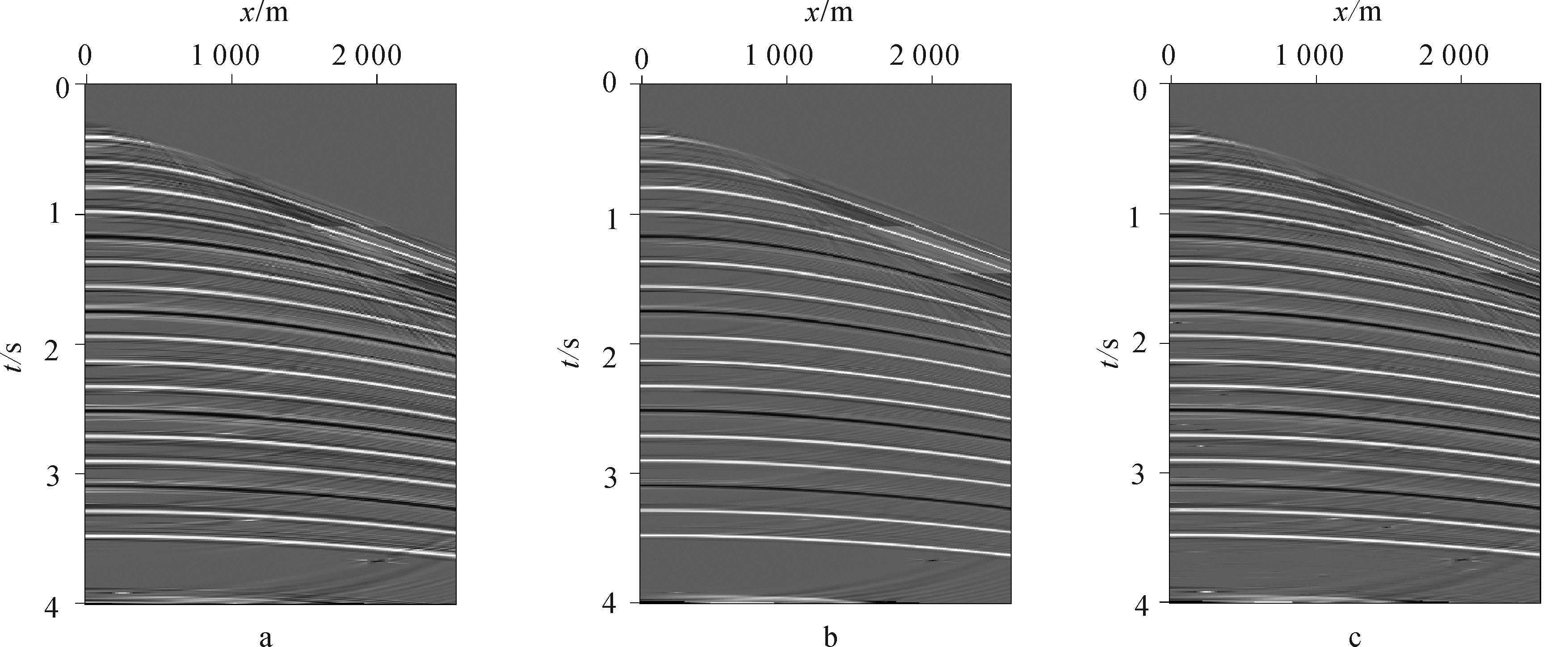
a. 硬阈值方法;b. 软阈值方法;a. 改进的阈值方法。图 5 不同阈值方法的处理效果比较 Fig. 5 Comparison of denoising results by using different threshold methods
方法 SNR/dB
低信噪比模型 -8.20
硬阈值方法 3.70
软阈值方法 3.11
改进的阈值方法 4.84 
a. 实际地震数据;b. 速度谱;c. 均方根速度;d. 新方法求得的局部地震倾角。图 6实际地震数据的局部地震倾角 Fig. 6 Local event slopes of field seismic data 
a. 基于时距关系的Seislet变换;b. 改进的阈值方法处理效果。图 7改进的阈值方法的处理效果 Fig. 7 Denoising results by using improved threshold method 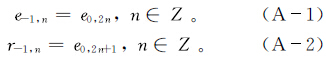



 的值与分解层数j无关。例如可以设计如下更新算子U来保证这一点:
的值与分解层数j无关。例如可以设计如下更新算子U来保证这一点:

| [1] | 张波, 印兴耀, 吴国忱, 等.用小波分析和反演方法联合去除随机噪声的研究[J].石油地球物理勘探, 1999, 34(6):635-641. Zhang Bo, Yin Xingyao, Wu Guochen, et al. Random Noise Elimination Using Wavelet Analysis and Inversion[J]. Oil Geophysical Prospecting, 1999, 34(6):635-641. |
| [2] | 王典, 刘财, 刘洋, 等.基于提升算法和百分位数软阈值的小波去噪技术[J]. 地球物理学进展, 2008, 23(4):1124-1130. Wang Dian, Liu Cai, Liu Yang, et al. Application of Wavelet Transform Based on Lifting Scheme and Percentiles Soft Threshold to Elimination of Seismic Random Noise[J]. Progress in Geophysics, 2008, 23(4):1124-1130. |
| [3] | 樊计昌, 刘明军, 王夫运, 等.小波包节点域和空间域倾角扫描高阶相关去噪技术[J]. 石油地球物理勘探, 2009, 44(6):695-699. Fan Jichang, Liu Mingjun, Wang Fuyun, et al. Dip Scanning High Order Correlation Denoise Technique in Wavelet Packet Node Field and Space Domain[J]. Oil Geophysical Prospecting, 2009, 44(6):695-699. |
| [4] | Zhang Yi, Cheng Lizhi. A New Wavelet Denoising Method of Seismic Signals Based on a Recursive Optimal Thresholding[J]. Acta Scientiarum Naturalium Universitatis Nankaiensis, 2011, 4:14. |
| [5] | 王志强, 韩立国, 巩向博, 等. 起伏地表检波器组合响应[J]. 吉林大学学报:地球科学版, 2014, 44(2):694-703. WangZhiqiang, HanLiguo, GongXiangbo, etal.GeophoneArrayResponseonUndulatingSurface[J].JournalofJilinUniversity:EarthScienceEdition, 2014, 44(2):694-703. |
| [6] | Chauris H, Nguyen T. Seismic Demigration/Migration in the Curvelet Domain[J]. Geophysics, 2008, 73(2):35-46. |
| [7] | Herrmann F J, Wang D, Hennenlent G, et al. Curvelet-Based Seismic Data Processing:A Multiscale and Nonlinear Approach[J]. Geophysics, 2008, 73(1):1-5. |
| [8] | Pennec E L, Mallat S. Sparse Geometric Image Representation with Bandelets[J]. IEEE Trans Image Process, 2005, 14(4):423-438. |
| [9] | Do M N, Vetterli M. The Contourlet Transform:An Efficient Directional Multiresolution Image Representation[J]. IEEE Trans Process, 2005, 14(12):2091-2106. |
| [10] | Starck J L, Candes E J, Donoho D L. The Curvelet Transform for Image Denoising[J]. IEEE Trans Image Process, 2002, 11(6):670-684. |
| [11] | Velisavljevic V. Directionlets:Anisotropic Multi-Directional Representation with Separable Filtering. Lausanne:Ecole Polytechnique Federale de Lausanne, 2005. |
| [12] | Fomel S. Towards the Seislet Transform[J]. SEG Extended Abstracts, 2006, 25(1):2847-2851. |
| [13] | Fomel S, Liu Y. Seislet Transform and Seislet Frame[J]. Geophysics, 2010, 75(3):25-38. |
| [14] | 刘洋, Fomel S, 刘财, 等.高阶Seislet变换及其在随机噪声消除中的应用[J].地球物理学报, 2009, 52(8):2142-2151. Liu Yang, Fomel S, Liu Cai, et al. High-Order Seislet Transform and Its Application of Random Noise Attenuation[J]. Chinese Journal of Geophysics, 2009, 52(8):2142-2151. |
| [15] | 张鹏, 陆文凯. 利用局部倾角的地震成像研究[C]//中国地球物理学会第二十六届年会、中国地震学会第十三次学术大会论文集. 宁波:中国地球物理学会, 中国地震学会, 2010. Zhang Peng, Lu Wenkai. Study of Seismic Imaging by Using Local Event Slopes[C]//Papers of the Twenty-Sixth Annual Meeting of Chinese Geophysical Society and the Thirteenth Academic Conference of Seismological Society of China. Ningbo:Chinese Geophysical Society, Seismological Society of China, 2010. |
| [16] | Fomel S. Applications of Plane-Wave Destruction Filter[J]. Geophysics, 2002, 67(6):1946-1960. |
| [17] | Bona A. Velocity-Less Migration Using Horizontal Slownesses[J]. EGU General Assembly, 2009, 11:EGU2009-3883. |
| [18] | Douma H. Leading-Order Seismic Imaging Using Curvelets[J]. Geophysics, 2007, 72(6):231-248. |
| [19] | Donoho D L, Johnstone J M. Ideal Spatial Adaptation by Wavelet Shrinkage[J]. Biometrika, 1994, 81(3):425-455. |
| [20] | Gao H Y, Bruce A G. WaveShrink with Firm Shrinkage[J]. Statistica Sinica, 1997, 7(4):855-874. |
| [21] | 李冲泥, 胡光锐.一种改进的子波域语音增强方法[J].通信学报, 1999, 20(4):88-91. Li Chongni, Hu Guangrui. A Modified Wavelet Domain Speech Enhancement Method[J]. Journal of China Institute of Communications, 1999, 20(4):88-91. |
| [22] | 许丽群.小波阈值去噪改进算法研究[J].电子测量技术, 2010, 33(8):43-45. Xu Liqun.Research of Improved Algorithm of De-Noising in Wavelet Threshold[J].Electronic Measurement Technology, 2010, 33(8):43-45. |
| [23] | 张新超. Seislet变换去除叠前线性干扰[D]. 成都:成都理工大学, 2009. Zhang Xinchao. Removal of Prestack Linear Noise by Seislet Transform[D]. Chengdu:Chengdu University of Technology, 2009. |
| [24] | Fomel S. Velocity-Independent Time-Domain Seismic Imaging Using Local Event Slopes[J]. Geophysics, 2007, 72(3):139-147. |
| [25] | Fomel S, Grechka V. Nonhyperbolic Reflection Moveout of P Waves:An Overview and Comparison of Reasons[M]. Golden:Center for Wave Phenomena Colorado School of Mines, 2001. |
| [26] | 邓玉娟.基于小波变换的语音阈值去噪算法研究[D].重庆:重庆大学, 2009. Deng Yujuan. Study of Threshold De-Noising Algorithm of Speech Signal Based on Wavelet Transformation[D]. Chongqing:Chongqing University, 2009. |
| [27] | 余晃晶.小波降噪阈值选取的研究[J].绍兴文理学院学报:自然科学版, 2004, 24(9):34-38. Yu Huangjing. Slection of a Wavelet Noise-Reduction Threshold[J]. Journal of Shaoxing University:Natural Science Edition, 2004, 24(9):34-38. |
| [28] | Claerbout, J F. Basic Earth Imaging:Stanford Exploration Project[EB/OL]. [2012-10-10].. |



