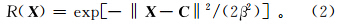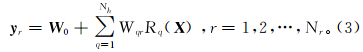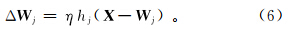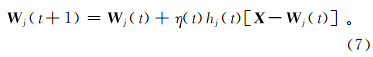2. 吉林大学地下水资源与环境教育部重点实验室, 长春 130021
2. Key Laboratory of Groundwater Resources and Environment, Ministry of Education, Jilin University, Changchun 130021, China
0 前言
浅层地下水水位的预测,可为水资源管理、城市规划、土木工程设计等提供重要的背景资料。因此,有关地下水水位预测的研究已成热点。传统的地下水水位预测方法采用简单的线性函数描述地下水水位的动态特征,但结果往往难以令人满意。随着学科的发展,地下水水位预测方法也不断演化进步。早在20世纪末、21世纪初,金菊良等[1]、Savic等[2]、Chen等[3]、杜超等[4]将数学模型应用于地质及水文地质预测和分类中,但这些模型的建立需要大量的参数和高质量的数据来刻画其物理过程,因而没有得到广泛应用。基于时间序列分析的模型也是地下水水位预测的一个重要工具,例如,Box 与Jenkins提出的传递函数模型(transfer noise model,TFN)[5],Hipel 和Mcleod提出的环境系统和水资源的时间序列模型(autoregressive exogenous variable model,ARX)等[6]。Knotters 和 Van Walsum[7]运用随机模型通过地下水埋深的时间序列估算水量的变化情况;Ahn 与 Salas[8]还介绍了一种运用在不同的时间间隔下非稳定地下水水位数据建立时间序列模型的方法,但由于时间序列模型过于突出时间序列,忽略了外界因素的影响,因而在预测过程中存在缺陷,当外界发生较大变化时,往往会有较大偏差。另外地质统计学的方法也被应用于地下水水位的预测中[9, 10]。
近年来,随着计算机技术的发展,基于大量运算的人工神经网络(artificial neural network,ANN)模型作为一种新的信息处理模式被运用于地下水水位预测中,且都取得了一定的成果[11, 12, 13]。理论上,人工神经网络是一种通用的近似函数,它可以在服从一定精度的条件下满足任意非线性的组合[14]。人工神经网络在地下水水位预测应用最多的是BP神经网络,但由于自身存在训练时间长、局部最小化、算法收敛速度过慢等缺点,逐渐被放弃使用。径向基函数神经网络(radial basis function neural network,RBFN)作为一种优越的多层前馈式神经网络,有着较高的运算速度和很强的非线性映射功能,可较好地克服上述问题,更适于非线性时间序列的预测问题;但对于RBFN,隐层节点的数目、隐层径向基函数的中心以及隐层径向基函数的宽度都是难以确定的,这就需要一种方法来确定上述参数。很多学者将聚类的思想应用于RBFN的优化设计中,提出了基于减聚类、K-means聚类、中心聚类和对手受罚的竞争聚类等拓扑结构的设计方法,取得了一系列的成果[15, 16, 17, 18, 19, 20]。自组织映射(self-organizing map,SOM)以其清晰的计算原则和简单的结构较好地弥补了RBFN自身的缺点。Chen Luhsienm等人[21]已经运用SOM-RBFN对地下水位进行了预测,但在其预测过程中仅用聚类来确定隐层节点的数目。隐层径向基函数的宽度通过下式计算:
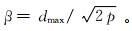
式中:β为径向基函数的宽度;dmax为节点之间的最大距离;p为隐层节点的数目。利用上式计算将导致RBFN隐层中径向基函数的宽度都是相同的,但事实并非如此。因此,笔者通过SOM神经网络对样本进行聚类,从而确定隐层节点数,并利用聚类后的结果求出径向基函数的中心及宽度,这样RBFN的隐层得到了更大程度的优化。 1 计算方法 1.1 径向基函数神经网络
RBFN由输入层(X)、隐层(H)、输出层(Y)3部分组成,其网络拓扑结构如图 1所示。RBFN从输入层到隐层的变换是非线性的,而从隐层到输出层的变换则是线性的。这种网络结构,隐层单元输出为
式中:Xi为第i个输入量;Cj是隐层第j个神经元的中心;‖·‖为欧氏范数;Rj(Xi)为第i个输入量在隐层中第j个神经元的输出;R( )为RBFN的基函数。
 |
| 图 1 RBFN结构 Fig. 1 Architecture of RBFN |
| |
基函数一般都是径向对称的,最常见的是高斯核函数,因此,式(1)可以表达为
式中:R(X)为输入向量X通过隐层节点C的输出;X=[X1,X2,…,XN]T,C=[C1,C2,…,CQ]。
输出单元即对隐节点的输出进行线性加权组合,并加一个偏移量,具体表达式如下:
式中:yr是输入向量X在输出层第r个节点的输出向量;Nr为输出层单元的数目;Nh为隐层节点的数目;Rq(X)是输入向量X在第q个隐层节点的输出向量;Wq r是连接第q个隐节点和第r个输出单元的权重;W0是偏移矢量[22]。 1.2 自组织映射
SOM也是神经网络的一种,它由输入层和输出层(竞争层)组成(图 2)。输入层的神经元数为N,竞争层是由M个神经元组成的一维或者二维平面阵列,也可以是更高维的,不过并不常见。
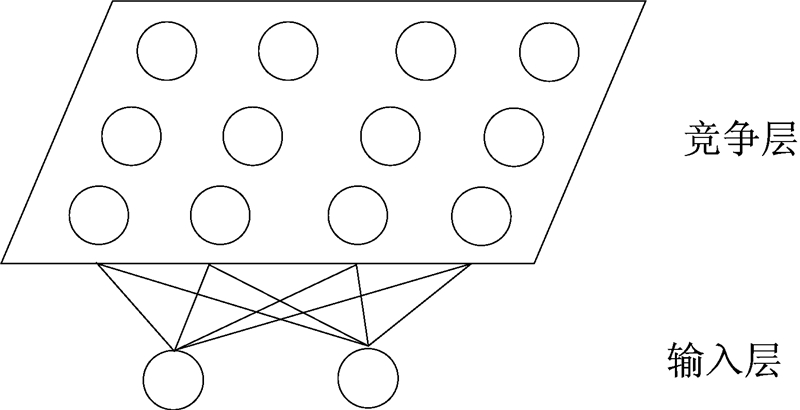 |
| 图 2 SOM神经网络结构 Fig. 2 Architecture of the SOM neural network |
| |
设输入向量为X=[X1,X2,…,XM]T,与输出层神经元j相应的权值向量Wj可以表示为Wj=[W1j,W2j,…,WMj]T,j=1,2,…,N。确定获胜输出层神经元,相当于选择权值向量Wj与输入向量X最为匹配的输出层神经元,即选出Wj与X具有最小欧氏范数距离dj的神经元作为获胜神经元,其计算公式为
邻域函数hj定义了围绕获胜神经元邻近区域的大小。典型的邻域函数为高斯函数:
式中:hj为拓扑邻域;σ是拓扑邻域的有效宽度;μj为第j个神经元;μj*为获胜神经元。
权值向量变化值ΔWj可由下式获得:
式中,η为学习率参数。
因此,权重的更新可以通过下式计算[23]:
式中,t为时间。
通过式(7)可以调整拓扑邻域内所有神经元的权值向量。通过对训练数据的反复运算,权值邻域不断更新,确定输入模式在竞争层中所对应的映射位置,并在一定范围内对权值进行调整。通过以上过程可以得到各类别集合的中心即获胜神经元,以及其相应的分布范围,即获胜神经元的邻域。SOM的具体输出可以通过一个二维网格表示,从中可以清晰地看到获胜神经元的位置,网格中每一个格代表的是在输出层中输入向量的位置。
至今还没有一个理论能确定最优的输出层网格大小,因此网格必须足够大,能够涵盖大量数据分类后所形成的子集合。对于迭代次数,通用的原则是至少在训练数据数的500倍以上[23]。 1.3 SOM-RBFN模型
SOM-RBFN设计由两步组成。
第一步:利用SOM神经网络对样本进行训练,记录每个样本在竞争层的映射位置,即所求获胜神经元;然后记录各获胜神经元的连接权值Wi*,将各获胜神经元权值组成集合记为Wg,即Wg=[W*i],i=1,2,3…,Mg,Mg表示获胜神经元的数目;并且找出各获胜神经元与映射到该神经元的所有样本的欧氏距离:
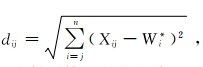
其中,Xij表示映射到第i个获胜神经元的第j个样本,j=1,2,3…,N。令ri=max{dij},则R=[ri]即为各聚类的半径。
第二步:将SOM竞争层各获胜神经元的连接权值向量Wg和所对应的聚类半径R传送到RBFN的隐层节点,Wg作为隐层径向基函数的中心C,相应的R就作为隐层径向基函数的宽度σ;然后再将已知样本X作为RBFN的输入向量,最终建立完整的RBFN模型,完成预测。 2 实例应用 2.1 研究区域概况
吉林市由4个行政区组成,分别为龙潭区、昌邑区、丰满区、船营区。本文所选长观井为丰满区二道乡2000-2009年地下水位观测资料。历年各月平均地下水位变化如图 3所示,共有120组水位数据。选择其中前108组作为训练数据,后12组作为验证模型数据。本文分别选择5、7、10 a的数据做3组训练预测,即分别记为RBF5、RBF7、RBF10,以考查数据长度对预测结果的影响。
 |
| 图 3 2000-2009年研究区地下水位动态变化曲线 Fig. 3 Time series plots for monthly average groundwater head data at the station from 2000 to 2009 |
| |
首先,利用K-S检验对数据集进行检验,判断其是否服从正态分布,通过SPSS19 计算得到在0.05的显著性水平下,数据检验统计值P=0.07,因此本数据集服从正态分布,符合RBFN中高斯核函数的应用。然后对训练数据进行预处理,即将它们分为3个输入量{X1,X2,X3},分别是月预测水位的前12个月平均水位,前13个月的平均水位,前1个月的平均水位,作为RBFN模型的3组决定预测的输入变量。
利用SOM神经网络对样本进行分类,使样本数据结构由高维降到低维,便于研究,但选择的目标网格要足够大,使其能较好地将样本进行分类。3组训练数据分别选用8×8、8×8、12×12的网格,SOM中连接输入层和竞争层的初始权向量设定在0和1之间,学习速率为0.1递减为0.01之间的不断变化值。分别经过2 400、3 600、5 400次迭代运算,SOM完成其对样本数据的分类,并在二维网格中反映出来。分类结果如图 4所示。 2.3 模型预测结果分析
从图 4a中可见,前期48组观测数据被分为7组,即隐层节点数为7,然后利用分类后的结果可以计算出Wg=[0.897 0.834 0.620 0.479 0.367 0.254 0.193],R=[0.421 0.386 0.360 0.206 0.188 0.237 0.178]。从图 4b中可以看出,前期72组观测数据被分为11组,即隐层节点数为11,利用分类后的结果计算出Wg=[0.906 0.857 0.755 0.644 0.540 0.483 0.423 0.345 0.297 0.235 0.173],R=[0.440 0.214 0.256 0.207 0.181 0.148 0.152 0.133 0.100 0.111 0.159]。同上,从图 4c中可以看出,前期72组观测数据被分为15组,分类后的计算结果Wg=[0.215 0.264 0.301 0.320 0.341 0.362 0.468 0.448 0.522 0.562 0.608 0.775 0.648 0.808 0.867],R=[0.203 0.091 0.083 0.082 0.311 0.144 0.143 0.182 0.164 0.142 0.120 0.288 0.288 0.189 0.497]。将这些参数分别代入各自的神经网络模型(RBF5、RBF7、RBF10)中,计算得出模拟期(2001-2008年)及2009年预测水位与实际水位的对比,如图 5所示。
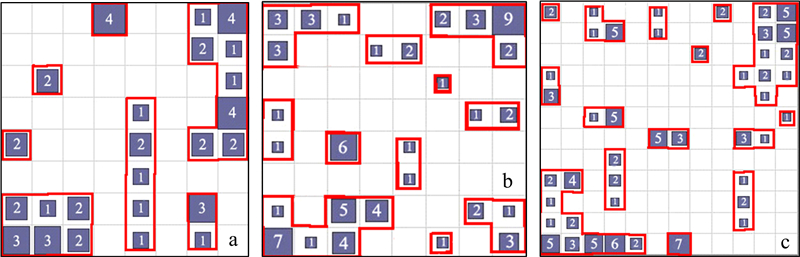 |
| a. RBF5;b. RBF7;c. RBF10。 图 4 观测井数据二维分类图 Fig. 4 2D feature map for the different models of the observation well |
| |
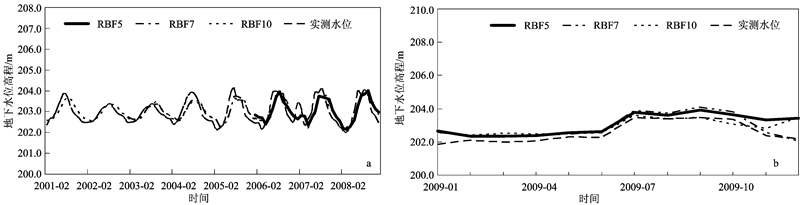 |
| a.训练数据;b.验证数据。 图 5 预测水位与实测水位对比 Fig. 5 Comparison of observed groundwater heads and forecasted values |
| |
从图 5中可以清晰地看出3个不同系列长度训练数据集和验证集的预测水位与实测水位的拟合情况。图 5a中易见,无论哪组拟合效果都不是很完美,例如峰值出现的时间存在一定的延迟或超前,但总体趋势基本符合。图 5b清晰地显示RBF7神经网络预测的地下水位与实测水位的拟合效果较优一些,RBF5和RBF10都是在曲线两端拟合偏差较大,从而导致了总体的拟合效果较差。具体拟合情况可以从均方根误差(RMSE)、有效系数(CE)评价标准来看(表 1)。均方根误差的数值越小代表实测数据与预测数据之间的差距越小,即预测效果越好;有效系数的值越大代表模型模拟精度越高。由表 1可知:3组训练数据在训练预测中,RBF7相比其他2个的预测结果更好;验证数据即2009年各月的预测水位的误差分析,也同样是RBF7数据拟合得最好,但仍有很大改进空间,它也只能做到在趋势上预估一个区间范围,毕竟地下水位变化除了与气象、下垫面等自然因素有关外,很大程度上还受地下水开采量变化影响;如果在研究区出现一种开采情况是与往年不同的,就可能会打破原有的预测模式,使预测结果产生较大偏差。总之,改进后的RBFN已经能够更简单有效地对地下水位进行预测了。
| 模型 | RMSE | CE | |
| 训练 | RBF5 | 0.41 | 0.62 |
| RBF7 | 0.36 | 0.62 | |
| RBF10 | 0.33 | 0.43 | |
| 平均值 | 0.37 | 0.56 | |
| 验证 | RBF5 | 0.51 | 0.30 |
| RBF7 | 0.40 | 0.74 | |
| RBF10 | 0.58 | 0.43 | |
| 平均值 | 0.50 | 0.49 |
通过SOM改进的RBFN预测地下水水位,解决了RBFN模型自身参数确定上的问题,实现了SOM-RBFN在地下水动态预测中的应用,并且对吉林市丰满区二道乡地下水水位进行了预测。由此得出如下结论:
1)SOM-RBFN可以作为预测地下水动态的简单而有效的工具,尤其是在资料相对缺乏的地区,能够在一定程度上为水资源管理提供参考。
2)将观测井动态资料分为3组,构成RBF5、RBF7、RBF10三组模型,分别训练模拟计算,最终发现RBF7的拟合结果更加理想,表明数据的多少并不能直接影响模型预测的结果,而是要看训练数据的组成是否和预测水位有更大的类似性,如果数据组成结构相差较远,会增大预测结果的误差。
3)从拟合效果上看,SOM-RBFN在预测地下水位的精度上仍有很大的提升空间,如何提高RBFN的适应能力仍是后续研究的重点,并且在今后的工作中将加入其他观测井资料,进一步观察模型预测结果与数据多少的关系。
| [1] | 金菊良, 杨晓华, 金宝明, 等.基于遗传算法的地下水位动态预测双线性模型[J].水科学进展, 2001, 12(3):361-365. Jin Juliang, Yang Xiaohua, Jin Baoming, et al. A Bilinear Time Series Model Based on Genetic Algorithm for Predicting Groundwater Level Regime[J]. Advances in Water Science, 2001, 12(3):361-365. |
| [2] | Savic D A, Walters G A, Davidson J W. A Genetic Programming Approach to Rainfall-Runoff Modeling[J]. Water Resour Manage, 1999, 13(3):219-231. |
| [3] | Chen S K, Mangimeli P, West D. The Comparative Ability of Self-Organizing Neural Networks to Define Cluster Structure[J]. Omega, 1995, 23(3):271-279. |
| [4] | 杜超, 肖长来, 吕军, 等.地下水水质实时预报系统开发及利用:以下辽河平原为例[J].吉林大学学报:地球科学版, 2014, 44(5):1625-1632. Du Chao, Xiao Changlai, Lü Jun, et al. Development and Application of Real Time Groundwater Quality Prediction System:An Example in Lower Liaohe River Plain[J]. Journal of Jilin University:Earth Science Edition, 2014, 44(5):1625-1632. |
| [5] | Box G E P, Jenkins G M. Time Series Analysis, Forecasting and Control[M]. San Francisco:Holden-Day, 1976. |
| [6] | Hipel K W, Mcleod A I. Time Series Modeling of Water Resources and Environmental Systems[M]. Amsterdam:Elsevier, 1994. |
| [7] | Knotters M, Van Walsum V. Estimation Fluctuation Quantities from Time Series of Water Table Depths Using Models with a Stochastic Component[J]. Journal of Hydrology, 1997, 197(1/2/3/4):25-46. |
| [8] | Ahn H, Salas J D. Groundwater Head Sampling Based on Stochastic Analysis[J]. Water Resour Res, 1997, 33(12):2769-2780. |
| [9] | Kumar D, Ahmed S. Seasonal Behaviour of Spatial Variability of Groundwater Level in a Granitic Aquifer in Monsoon Climate[J]. Current Science, 2003, 84(25):188-196. |
| [10] | Gundogdu K S, Guney I.Spatial Analyses of Ground-water Levels Using Universal Kriging[J]. Journal of Earth System Science, 2007, 116(1):49-55. |
| [11] | Nag A K, Mitra A. Forecasting the Dailu Foreign Exchange Rates Using Genetically Optimized Neural Networks[J]. Journal of Forecasting, 2002, 21(7):501-511. |
| [12] | Zhang G, Patuwo B E, Hu M Y. Forecasting with Artificial Neural Networks:The State of the Art[J]. International Journal of Forecasting, 1998, 14(1):35-60. |
| [13] | Bulsari A, Saxen H. Nonlinear Time Series Analysis by Neural Networks:A Case Study[J]. Int J Neural Syst, 1993, 12(1):1-10. |
| [14] | Atiya A F. Prediction for Credit Risk Using Neural Networks:A Survey and New Results[J]. IEEE Trans Neural Netw, 2001, 12(4):929-935. |
| [15] | 孟艳, 潘宏侠.PSO聚类和梯度算法结合的RBF神经网络优化[J].自动化仪表, 2011, 32(2):6-8. Meng Yan, Pan Hongxia. Optimization of RBF Neural Network Based on Combination of PSO Clustering and Gradient Algorithms[J]. Process Automation Insterumentation, 2011, 32(2):6-8. |
| [16] | 朱明星, 张德龙. RBF网络基函数中心选取的算法研究[J]. 安徽大学学报:自然科学版, 2000, 24(1):72-74. Zhu Mingxing, Zhang Delong. Study on the Algorithms of Selecting the Radial Basis Function Center[J]. Journal of Anhui University:National Science Edition, 2000, 24(1):72-74. |
| [17] | 方力智, 张翠芳, 易芳.基于改进差分进化算法的RBF神经网络优化方法[J].成都大学学报:自然科学版, 2009, 28(3):231-234. Fang Lizhi, Zhang Cuifang, Yi Fang. Optimization Approach Based on Modified Differential Evolution Algorithm for RBF Neural Network[J]. Journal of Chengdu University:Natural Science Edition, 2009, 28(3):231-234. |
| [18] | 张江涛, 刘旭敏.一种基于代数算法的RBF神经网络优化方法[J].计算机工程与应用, 2008, 44(5):96-98. Zhang Jiangtao, Liu Xumin. Optimization Approach Based on Algebraic Algorithm for RBF Neural Network[J]. Computer Engineering and App-lications, 2008, 44(5):96-98. |
| [19] | 马洪伟, 赵志刚, 吕慧显, 等.基于蚁群聚类和裁剪方法的RBF神经网络优化算法[J].青岛大学学报:工程技术版, 2008, 23(3):35-38. Ma Hongwei, Zhao Zhigang, Lü Huixian, et al. Optimization Algorithm of RBF Neural Networks Based on Ant Colony Clustering and Pruning Method[J]. Journal of Qingdao University:Engineering and Technology, 2008, 23(3):35-38. |
| [20] | 涂松, 贲可荣, 徐荣武, 等.采用SOM和RBF优化下的水下航行器噪声源识别[J]. 计算机工程与科学, 2007, 29(10):112-114. Tu Song, Ben Kerong, Xu Rongwu, et al. Identification of the Acoustic Fault Sources of the Underwater Vehicles Based on the SOM and RBF Neural Network Optimization[J]. Computer Engineering & Science, 2007, 29(10):112-114. |
| [21] | Chen Luhsienm, Chen Chingtien, Pan Yangu.Ground-water Level Prediction Using SOM-RBFN Multisite Model[J]. Journal of Hydrologic Engineering, 2010, 15(8):624-625. |
| [22] | ASCE Task Committee on Application of Artificial Neural Networks in Hydrology. Artificial Neural Network in Hydrology[J]. Journal of Hydrologic Eng, 2000, 5(2):142-137. |
| [23] | Haykin S.Neural Networks:A Comprehensive Foun-dation[M]. London:Macmillan, 1994. |