2. 吉林大学建设工程学院, 长春 130026
2. College of Construction Engineering, Jilin University, Changchun 130026, China
0 引言
冻土是一种特殊的土体,它的固相由固体颗粒和冰共同组成。冻土可以视为多孔介质,冻土中水分的迁移流动亦属于多孔介质流体流动,对冻土中水分迁移的研究也可以应用多孔介质理论[1, 2, 3, 4]。因此,冻土的水、热迁移与成冰过程的本质即为多孔多相介质带相变的固、液、气、热耦合问题。1957年,Philip和de Vries[5]基于多孔介质中液态水黏性流动及热平衡原理,提出了水热耦合迁移模型,开创了土中水热耦合研究的先河。此后Aboustit等[6]相继对冻土中水热迁移耦合模型进行了研究。国内对冻土水热耦合迁移问题的研究起步较晚,当前主要集中在研究正冻土尤其是饱和正冻土中水热迁移问题等方面[7],对非饱和季节冻土的水热迁移耦合问题研究较少[8, 9, 10, 11],目前仍存在一些诸如不能很好地模拟自然界边界条件、水分迁移的机制不确定及水分迁移过程的数值模拟与模型计算过于简单等问题。本文对笔者建立的一个基于多孔介质理论的水热迁移耦合模型[12, 13]进行求解,并将结果与实例进行对比,从而验证模型的可靠性,以使模型能更好地模拟实际情况,解决实际问题。 1 模型求解基础 1.1 原始模型方程
所求解的原始模型方程[13]如下:
式中:t为时间;T为温度;ρd为土粒干密度;e为孔隙比;ρs为土粒密度;ρl为水的密度;θl,θi,θ分别为液态含水率、含冰率以及总含水率;C为骨架热容;hi,l为水的冻结(或冰融解)潜热;λl,λi,λs分别为液态水、冰及土骨架导热系数;cl,ci分别为液态水和冰的比热;Dl为液态水扩散系数;Kl为液态水渗透系数。 1.2 修正模型方程
为了方便对模型进行求解,对模型进行如下修正。根据控制方程式(1)和(2),考虑到由于温度变化造成水分的相变和迁移,引入阶跃函数H(x)(Heaviside函数)作为相变指示函数f(T),有
则总含水率为
水分控制方程(1)可改写为
温度传递方程(2)可改写为
将式(6)两边同时乘以hi,l再代入(7)得
根据未冻含水率和温度的关系式θl=θl(t,T),得
式(9)代入式(8)得
代入阶跃函数H(x),由式(7)得
代入阶跃函数H(x),由式(8)得
式(5)、(10)、(11)、(12)即为修正的模型控制方程,对方程采用有限元法进行二维求解,即可得到数值解。 1.3 模型参数确定
为了保持单位的一致性,文中所有参数一律采用国际单位制。部分参数采用在长春-松原一级公路线段采取的土样进行相关试验及观测后得到的数值。
1)已知参数
λl=0.574 5 W/(m·K),λi=2.1 W/(m·K),cl(288 K)=1.002 J/(kg·K),ci=0.505 J/(kg·K),hi,l=334 kJ/kg。
2)实验测定参数
液态水扩散系数与体积含水率的关系式为
Dl=1.205e+4θl10.5,
相关度为0.944 8。
土体导热系数与温度的关系拟合式为
λs=-0.006 6T+3.198 9。
未冻含水率与温度的关系拟合式为
θl= 4.1e-64T25.696 。
导水系数与未冻含水率的拟合关系式为
K=Cw(1.205 4e+4θl 10.5),
其中,Cw =1 500 kJ/(m3·K)。
当温度为291 K时,骨架比热cs=830 J/(kg·K),当温度为263 K时,cs=763 J/(kg·K)。
C可视为体积含水率和体积含冰率的函数:

模型的求解以长春地区的参数为基础。长春地区冬季严寒、漫长,冻结期长达5个多月。标准冻深约1.7 m,为典型的温带气候区。选取长春-松原公路段土样的相关参数,利用所建立的模型对其进行求解,模拟长春地区季节冻土的冻结发展情况,研究土体中不同深度、不同温度下的水分迁移过程。
参考长松线公路野外监测结果,将模型的深度下限定为3.0 m,宽度取1.0 m。因为所监测地点为公路地段,地面有50 cm的路面层,监测数据为从地表以下0.5 m处开始,所以计算模型上部边界选取深度为0.5 m处。由于本区地下水埋深在7.0 m左右,埋深较大,毛细水无法为冻结区补给水分,且热量和孔隙水均沿垂直向运移,水平向的热和孔隙水交换量很小,所以可以将水热迁移视为一维问题。模型初始温度模型示意图如图 1所示。模型条件如下。
 |
| 图 1 土柱模型示意图 Fig. 1 Chart of the soil column model |
| |
1)初始条件
温度T(t=0,y)=10.3℃=283.3 K;含冰率θi=0;总含水率θ=2.571y4-11.285y3+10.584y2+3.810y+19.422。
2) 边界条件
模型顶端温度属于第一类边界条件,但由于温度随时间变化,根据现场实际监测结果进行拟合得到
T(t,y=0.5)=264.3+3e-6t 。
底端温度属于第二类边界条件:

总含水率θ、含冰率θi在模型两端均为第二类边界条件:
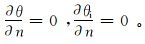
模型采用有限元进行求解,模拟的过程包括从刚入冬时的不稳定冻结阶段一直到气温回升之后的双向融化阶段(即2004-2005年),共5个月,所得结果如下。 2.2.1 冻结过程中的温度变化
图 2为冻结1~5月的土柱温度分布曲线,图 3为冻结第5月的土柱温度分布和传递方向。由图 2可见:1)冻结第1月,土体温度分布比较均匀,上部温度较低,下部温度较高,此时冻结锋面位于顶部。这是因为现在的趋势为在土柱中部分开,下部土体温度向上部传递,上部土体温度向下部传递。2)冻结第2月,土体上部负温区(T<237 K)开始增大,说明温度向下部传递。而此时冻结锋面已经明显下移。3)到第3月时,土体负温部分继续下移,在土体最上部以及中间部位开始出现升温的现象,但并不明显。4)到达第4月时,土柱负温区开始缩小,并且在土柱上部开始有正温区的出现,此时冻结锋面以上的温度传递方向为负温向上传递。冻结锋面以下土体温度继续向下传递。5)到第5月时,地表温度早已达到正温,从土柱中也可以看出,正温区明显增多,负温区变小,此时地表出现温度不稳定区。从图 3亦可以看出,此时土柱中温度传递方向整体向下,但靠近地表处温度传递方向略显凌乱,与图 2显示了相同的趋势。
 |
| 图 2 冻结1~5月的土柱温度分布曲线 Fig. 2 Temperature curve of the soil column frozen for 1-5 months |
| |
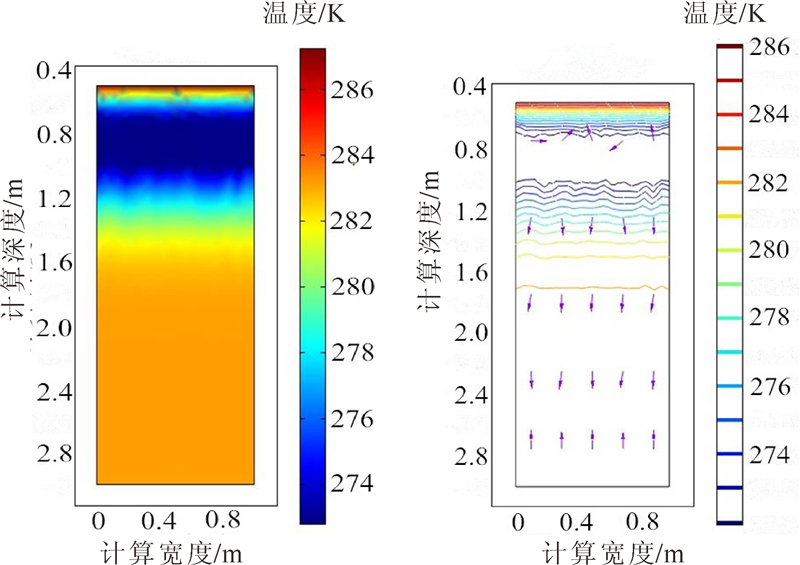 |
| 图 3 冻结第5月的土柱温度分布和传递方向 Fig. 3 Temperature gradient distribution and transmission direction of the soil column frozen for five months |
| |
图 4为冻结1~5月的土柱含水率分布曲线,图 5为为冻结第5月的土柱含水率分布和传递方向。由图 4可见:1)在第1月,土柱中以1.0 m深度左右为分界线,上部土体中的水分向下迁移,下部土体中的水分向上迁移。2)到第3月时,可以看出水分迁移仍具有第1月时的趋势,且此时的1.0 m上部的含水率数值比第1月时有所增大。1.0 m以下部分含水率均有所减小。3)到第5月时此趋势更加明显,地表含水率的数值比冻结第1月时明显增大,1.0 m下部的也继续减少。由图 5也可以看出,土柱中1.0 m以上水分向上迁移,而1.0 m以下有一个向下迁移的趋势。这是因为随着温度的降低,土体中负温开始从地表向下传递,同时土体由地表向下冻结,当上部土体冻结成冰后,其下部土体中的水分必然向上迁移对其补充。本区地下水埋深在7.0 m以下,所以毛细水无法供给水分迁移,因此导致1.0 m下部的土体含水率减小。
 |
| 图 4 冻结1~5月的土柱含水率分布曲线 Fig. 4 Moisture content curve of the soil column frozen for 1-5 months |
| |
 |
| 图 5 冻结第5月的土柱含水率分布和传递方向 Fig. 5 Moisture content gradient distribution and transmission direction of the soil column frozen for five months |
| |
为了对求解结果进行检验,将计算值与监测值进行对比。文中所采取的地温监测数据为与计算模型采用的土样一致的长松线2004-2005年度的地温监测结果。地温监测采取钻孔分段埋设探头,根据需要按规定的时间进行读数,精度0.5℃。
冻结第1、3、5月时计算的土体温度与实测的土体温度对比见图 6。从图 6可以看出,整体上模型计算值与实测值的趋势是一致的,但是存在误差,且随着冻结时间增长,误差值有减小的趋势,模型计算值更加接近实测值。
 |
| 图 6 冻结第1、3、5月土柱温度实测与计算对比图 Fig. 6 Temperature comparison chart of measurement and calculation frozen for one,three and five months |
| |
冻结第1、3月时皆是计算值中土层深度存在一个分界区,此区域上部模型计算值比实测值大,下部计算值比实测值小。在冻结第1月时,总体上以深度为2.0 m处为分界线,2.0 m以上计算结果比实测值大,2.0 m以下计算结果比实测值小,最大误差值达2℃左右。第3月时分界区域有所上移,但趋势基本一致,且误差有比冻结第1月时减小的趋势。
土体冻结第5月,即计算与观测的最终结果时,从图 6中可以看出,模型计算结果与实测结果吻合得较好,变化趋势基本一致,误差只有1.0℃左右。从对地温要求的角度来说,这个误差范围是可以接受的,因为更重要的是了解温度变化的趋势,因此误差满足要求。
从以上3个不同时间段计算结果与实测结果的对比结果可以得出,所建立的模型可以较好地预测终值情况,虽然中间的情况误差较大,但是趋势基本一致。
可能导致出现这种现象的原因很多。例如:监测深度的密度不够大,以致于有些可能存在的温度突变点没有监测出来;模型用于计算的实测温度变化曲线为对现有的几个温度监测数据进行拟合的结果,必然存在一定的误差;土体的各种参数都是取样后室内测定的,存在一定误差;在现实中,天气等各方面因素的变化都可能导致气温的不稳定性,气温的变化必然导致土体温度的变化;而且路基上道路行车等给路基带来的荷载效应等都会导致计算结果与实测结果有差异。因此,为使模型能更加符合千变万化的实际情况,今后应该对这些方面做进一步的研究。 3.2 计算土体含水率与实测值对比
文中所采取的实测值为与计算模型采用的土样相同的长松线2004-2005年度的含水率监测结果。
土体的计算含水率值与实测值在冻结第1、3、5月时的比较情况见图 7。由图 7可知,3个冻结时间段基本上都是计算结果小于实测结果,但是整体上计算结果与实测结果的变化趋势还是比较一致的;和温度计算结果一样,同样是土层中部深度处模拟较好,上部和下部误差较大,而且同样模型的计算结果和最终值吻合得较好,误差最小,平均只有2%左右,这说明模型计算结果的终值能较好地模拟实际情况。
 |
| 图 7 冻结第1、3、5月含水率实测与计算对比图 Fig. 7 Moisture content comparison chart of measurement and calculation frozen for one,three and five months |
| |
对作者建立的水热迁移耦合模型进行修正,以长春-松原公路路段土样为基础,确定了模型参数,在一定假设的基础上,进行了数值求解,得到了土体冻结过程中温度及含水率在不同深度以及不同时间上的分布、变化情况。并将求解结果与长春-松原公路路段实际监测结果进行了对比。
根据对比结果,对于温度和含水率,模型的计算结果都与实测结果的趋势基本一致,但存在一定误差,整体上位于精度范围内。误差出现的原因可能如下:1)模型的建立是为了对现实情况进行模拟,但自然界是千变万化的,不可能对其所有的参数进行量化,且模型的建立需要考虑的因素甚多,在模型建立的过程中,为了方便计算、求解,必然会对实际情况进行一些简单化处理,也就是预先设定一系列的假设。本次所求解的模型在建立时就进行了一系列的假设,这必然会给模型的计算结果带来误差。2)模型的求解是建立在实测的土体参数基础上的,因此参数测定的准确与否对模型解的正确性也起着决定性的作用。冻土作为一种复杂的多相体,涉及到水热的对流、传导、相的转变等一系列物理化学过程,而能代表这些变化的热交换参数和水力参数测定的准确性却至今是个难点,而这些测定结果又对最终的计算结果影响较大,因此也会带来较大的误差。且土体随着深度的变化,各种参数也会有所变化,本次研究中为了方便模型的求解,对土体各个深度都采用了相同的参数,这样的处理必然也会给计算结果带来误差。3)模型的计算结果是与实际监测值进行对比,而实际监测值受监测方法、仪器精度等各种因素的影响,本身也存在一定误差。4)现实的自然界是复杂多变的,道路上覆积雪的融化向下渗流会对含水率的分布造成很大影响,而且作为路基,土体中的水分迁移过程将受车辆等外部动荷载作用,同时土体变形(压密、冻胀)造成的应力场对水分迁移也有影响。而这些在模型中都是无法反映的,因此计算结果与实测结果会有一定的误差。
多种因素可导致模型计算结果与实测结果有出入,如何在模型中将各种影响因素考虑进去以缩小误差,将结果控制在合理的区间内需要进一步研究。例如:可以在模型中考虑积雪融化入渗对水分迁移的影响;利用更合理、准确的方法对土体的各种参数进行测定;可以将由冻胀产生的力引入到模型中建立水热力耦合模型等。这些都是将来可以继续研究的问题。
| [1] | 朱志武, 宁建国, 马巍. 土体冻融过程中水、热、力三场耦合本构问题及数值分析[J]. 工程力学, 2007, 24(5):138-144. Zhu Zhiwu, Ning Jianguo, Ma Wei. Constitutive Model and Numerical Analysis for the Coupled Problem of Water, Temperature and Stress Fields in the Process of Soil Freeze-Thaw[J]. Engineering Mechanics, 2007, 24(5):138-144. |
| [2] | 罗焕炎, 陈雨孙. 地下水运动的数值模拟[M]. 北京:中国建筑工业出版社, 1988. Luo Huanyan, Chen Yusun. Numerical Simulation of Groundwater Movement[M]. Beijing:China Building Industry Press, 1998. |
| [3] | Bear J, Bechmat Y. Introduction to Modeling of Transport Phenomena in Porous Media[M].:Kluwer Academic Publishers, 1991. |
| [4] | 林瑞泰. 多孔介质传质传热引论[M]. 北京:科学出版社, 1995. Lin Ruitai. Heat and Mass Transfer in Porous Media Introduction[M]. Beijing:Science Press, 1995. |
| [5] | Philip J R, De Veries D A. Moisture Movement in Porous Material Under Temperature Gradient[J]. Trans Am Geophys Union, 1957, 38:222-232. |
| [6] | Aboustit B L, Advani S H, Lee J K, et al. Finite Element Evaluation of Thermo-Elastic Consolidation[J]. Proc US Symp Rock Mech, 1978, 23:587-595. |
| [7] | 周家作, 李东庆, 房建宏, 等. 开放系统下饱和正冻土热质迁移的数值分析[J]. 冰川冻土, 2011, 33(4):791-795. Zhou Jiazuo, Li Dongqing, Fang Jianhong, et al. Numerical Analysis of Heat and Mass Transfers in Saturated Freezing Soil in an Open System[J]. Journal of Glaciology and Geocryology, 2011, 33(4):791-795. |
| [8] | 陈飞熊, 李宁, 程国栋. 饱和正冻土多孔多相介质的理论构架[J]. 岩土工程学报, 2002, 24(2):213-217. Chen Feixiong, Li Ning, Cheng Guodong. Theoretical Framework Freezing Soil Saturated Porous Media Multiphase[J]. Chinese Journal of Geotechnical Engineering, 2002, 24(2):213-217. |
| [9] | 白冰, 刘大鹏. 非饱和介质中热能传输及水分迁移的数值积分解[J]. 岩土力学, 2006, 27(12):2085-2089. Bai Bing, Liu Dapeng. Numerical Integral Solutions of Heat Transfer and Moisture Transport in Unsaturated Porous Media[J]. Rock and Soil Mechanics, 2006, 27(12):2085-2089. |
| [10] | 吴晓玲, 向小华, 王船海, 等. 季节冻土区融雪冻土水热耦合模型研究[J]. 水文, 2012(5):12-15. Wu Xiaoling, Xiang Xiaohua, Wang Chuanhai, et al. Numerical Modeling for Coupled Snowmelt and Frozen Soil in Seasonally Frozen Soil Region[J]. Journal of China Hydrology, 2012(5):12-15. |
| [11] | 宿晓萍, 王清, 王文华, 等. 季节冻土区盐渍土环境下混凝土抗冻耐久性机理[J]. 吉林大学学报:地球科学版, 2014, 44(4):1244-1253. Su Xiaoping, Wang Qing, Wang Wenhua, et al. Frost Resistance and Durability Mechanism of Concrete Under Saline-Alkali Condition in Seasonal Frozen Soil Area[J]. Journal of Jilin University:Earth Science Edition, 2014, 44(4):1244-1253. |
| [12] | 李杨.基于多孔介质理论的季节冻土水热迁移耦合模型推导[J]. 河北工程大学学报:自然科学版, 2012(3):11-14. Li Yang. Derivation of Water and Thermal Migration Coupled Model Based on Theory of Porous Media in Seasonal Frozen Soil[J]. Journal of Hebei University of Engineering:Natural Science Edition, 2012(3):11-14. |
| [13] | 李杨. 季节冻土水分迁移模型研究[D]. 长春:吉林大学, 2008. Li Yang. A Study on the Moisture Content Migration Model of Seasonal Frozen Soil[D]. Changchun:Jilin University, 2008. |
















