2. 青岛理工大学土木工程学院, 山东 青岛 266033
2. School of Civil Engineering, Qingdao University of Technology, Qingdao 266033, Shandong, China
0 引言
近40年来,我国有超过100个冻结法施工的混凝土井筒发生破坏,给煤矿造成巨大经济损失[1-5]。上述破坏井筒均具有以下特征:一是地质条件类似,破裂井筒所处地层深厚松散层厚度在150~200 m之间;二是井筒所处含水层水位大幅降低,地下水水位下降超过10 m[1-5]。工业试验表明[5],底部含水层水位下降时,井筒顶部和地表沉降值增加,底部含水层水位不变时,井筒顶部和地表沉降值基本没有增加;这说明地下水水位升降与井筒破坏直接相关,必须开展二者之间关系研究。
为解释深厚松散地层煤矿井筒破裂机理,学者提出3种假说[4-7]:渗流变形假说、新构造运动假说和附加力假说。渗流变形假说[4-5]认为,煤层开采导致深厚松散地层的底部含水层排水产生动水圧力,从而诱发底部砂层发生机械潜蚀和渗流液化,土层发生层间滑动导致井筒破坏。新构造运动假说[4]认为,新构造运动改变井筒区域构造应力场,在软硬土层接合位置(松散层与基岩风化带)水平构造应力产生应力集中,导致井筒破坏。被广泛认同的附加力假说[6-7]认为,井筒破坏的主因是含水层水位下降致使致砂层固结压缩,土体与井壁之间的不均匀沉降导致井筒外壁产生竖向负摩阻力(也称为竖向附加力),不断增加的负摩阻力导致井筒承受的竖向应力超过自身承载极限而发生破坏。
附加力假说经过工程实践和模型试验得到验证后,针对不同井筒的实际地质条件,学者对竖向附加力分布特征开展了研究,包括采用理论推导[6]、数值模拟方法[7]、相似材料试验[8]等确定不同类型土层、不同埋深条件下的附加力分布规律和解析公式。上述研究不仅极大推进了井筒破坏机制的研究,还对井筒破坏的预防性治理工作提供了思路。
在混凝土井筒的损伤模型方面:彭向和等[9]改进了混凝土各向异性损伤模型,分析了三轴复杂路径下的混凝土力学响应;张楠等[10]开展了混凝土三轴压缩渗透性试验,给出了混凝土渗透性与损伤的相关经验公式;荣传新等[11]提出混凝土井壁的弹塑性损伤力学模型,给出了井壁承受的水压力与塑性损伤区半径之间关系;吴月秀等[12]建立了冻结井壁的各向异性损伤模型,模型考虑了温度、施工条件、混凝土骨料等对井壁质量的影响。井筒的损伤模型多是建立在混凝土试块室内试验基础上的,采用峰值强度前为弹性、峰值强度后为损伤的双线性模型。由于40年前修建井筒采用的混凝土质量要远低于现在的混凝土质量,现在也无法实现重复性试验,不能获取其准确的物理力学参数。因此,损伤变量的确定和校验非常困难。
为确保深厚松散地层煤矿井筒长期运营不发生破坏,很多井筒都提前开展了预防性治理工作[13-16],其中开设卸压槽是井筒预防性治理常用的措施之一,但目前缺乏预防性治理后井筒的安全评价标准,无法正确评价治理后井筒的安全状态。本文提出采用数值极限应变方法建立卸压槽治理井筒破坏判据,计算了极限状态下卸压槽治理井筒的潜在破坏位置和相应的地下水水位,并采用监测数据对计算结果进行验证。
1 混凝土井筒破坏的塑性极限应变判据 1.1 塑性极限应变理论概念材料变形过程中,从弹性状态进入塑性状态时,塑性发展到一定程度材料发生破坏,即应变达到塑性极限应变时认定材料破坏。塑性极限分析方法采用应变表述的理想弹塑性模型应力-应变关系,材料初始屈服时具有弹性极限应变γy,初始屈服后塑性应变逐渐增大,破坏时具有塑性极限应变γf,屈服和破坏可以明确区分。综上认为,材料的塑性极限应变可作为破坏准则[17-18],凡是达到材料塑性极限应变的点即认为该点发生破坏,该方法在边坡和隧洞工程中已经得到成功应用[17-19]。
阿比尔的采用广义塑性力学理论,结合M-C准则给出了岩土类摩擦材料的极限应变公式[19],其中:
弹性极限剪应变
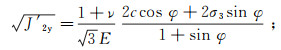 (1)
(1) 塑性极限剪应变
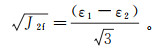 (2)
(2) 式中:ν为泊松比;E为弹性模量,MPa;c为黏聚力,MPa;σ3为侧向压应力,MPa;φ为内摩擦角, (°);ε1和ε2分别为轴向主应变和侧向主应变。
1.2 混凝土材料的塑性极限应变混凝土材料属于岩土类摩擦材料,可通过黏聚力和内摩擦角确定混凝土抗剪强度,只是尚无统一的标准试验方法。丛宇等[20]将直剪试验与单轴抗压试验结合,给出了混凝土材料的黏聚力和内摩擦角计算方法,计算结果与混凝土规范给出的强度值基本一致。
混凝土材料的极限应变一般指峰值应力对应的应变值,可通过试验测得。采用数值极限方法分析时,当混凝土材料中的某个单元达到塑性极限应变,可作为混凝土材料点破坏的判据。具体过程是:
1) 将混凝土材料视为岩土类摩擦材料,采用直剪试验与单轴抗压试验结合的方法,求出混凝土试块的c和φ[20]的关系式为
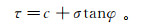 (3)
(3) 式中:τ为剪切应力,MPa;σ为正应力,MPa。
通过单轴抗压强度莫尔圆确定φ值,公式为
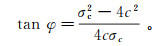 (4)
(4) 式中:σc为抗压强度,MPa。φ值取式(3)与式(4)中的较小值。
2) 建立混凝土标准试块数值计算模型,采用超载法不断增加竖向压力,直至数值计算不收敛,此时荷载为混凝土试块的单轴抗压强度,相应的应变值为混凝土试块的塑性极限应变。数值极限应变方法模拟的混凝土试块破坏形式与室内试验模拟的基本相同[19],获得的混凝土试块强度值与规范值也基本相同。
1.3 混凝土井筒整体破坏的塑性极限应变判据任何一个结构的破坏都是从一个点的破坏开始的,但是结构内部一个或者几个点的破坏不能导致结构的整体破坏,其结果只是结构整体承载能力的降低。对混凝土井筒而言,由于受到相邻混凝土材料的约束,井筒内一个点的破坏不会导致井筒发生整体破坏,即使几个点的破坏导致井筒内出现局部裂缝,井筒仍可以继续承载。只有井筒某一区域内达到极限应变值的破坏点发展至整体贯通,井筒出现贯通性裂缝,且数值计算不收敛时,井筒才会发生整体破坏,此时井筒完全丧失承载能力。该判据即为混凝土井筒整体破坏判据。
2 深厚松散地层泄压槽治理井筒概况 2.1 卸压槽法井筒治理技术卸压槽法治理混凝土井筒是在井筒内壁开设一环形槽,采用软木或PVC软板进行充填,在井筒内壁形成一道可压缩结构。当井筒底部地下水水位下降造成上部土体压缩时,井筒和周围土体接触会产生向下的附加力;此时由于卸压槽的可压缩性,压力作用时卸压槽会产生压缩变形,井筒与周围土体的相对沉降量减小,减小了土体压缩给井筒作用的竖向附加力,即可降低井筒发生破坏的概率。
2.2 卸压槽治理井筒实例介绍某煤矿所处地层第四系上覆深厚松散层厚度185 m,主要是黏土和砂土。该煤矿井筒1993年建设,深度586 m。井筒为C40混凝土结构,内半径4 000 mm,外半径5 150 mm,原混凝土壁厚1 150 mm。2004年竖井井筒在深度157.6 m进行了泄压槽预防性治理措施。卸压槽沿井筒环向布置一圈,厚度600 mm,高450 mm,卸压槽治理后井壁厚度550 mm。充填材料为防腐松木,上下两层木块交错叠放(图 1)。

|
| R4 600.内半径4 000 mm+泄压槽厚度600 mm。 图 1 卸压槽剖面示意图 Fig. 1 Schematic diagram of stress-relief groove |
|
|
井筒为轴对称结构,数值计算模型取1/4井筒(图 2),计算模型高度取113 m,其中基岩上方103 m,基岩厚度10 m,模型上部82 m土层和井筒自重视为均布荷载,井筒周围岩土体水平方向计算长度30 m。采用摩尔-库伦强度准则,井筒与土体设置接触单元模拟二者相互作用。模型边界为约束水平方向位移,底部固定。井筒、卸压槽的材料参数见表 1、表 2,混凝土极限应变值按照规范给出的表 3取值[20]。采用FLAC3D程序中的水力耦合模块,通过数值极限应变方法确定井筒破坏时的水位下降值,给出井筒破坏区域。考虑到混凝土井筒与周围岩土体有相对移动,井筒及周围岩土体施加接触面模拟它们之间的相互作用。

|
| 图 2 泄压槽治理井筒计算模型 Fig. 2 Calculation model of shaft |
|
|
| 名称 | 埋深/m | 体积模量/ MPa | 剪切模量/ MPa | 重度/(kN/m3) | 摩擦角/(°) |
| 粗砂层1 | 10.7 | 100 | 20 | 21 | 30 |
| 砂质黏土层 | 31.9 | 20 | 12 | 20 | 25 |
| 粗砂层2 | 13.5 | 100 | 20 | 20 | 30 |
| 粉质黏土层 | 19.7 | 35 | 20 | 20 | 25 |
| 粗砂层3 | 16.1 | 100 | 20 | 19 | 30 |
| 黏土层 | 9.4 | 81 | 37 | 22 | 20 |
| 井壁 | 111.3 | 15 000 | 12 000 | 25 | 62 |
| 卸压槽深度/mm | 卸压槽厚度/mm | 重度/(kN/m3) | 剪切模量/MPa | 体积模量/MPa |
| 450 | 600 | 5 | 150 | 100 |
图 3、4为不同地下水水位下降值对应的井筒剪应变云图。对带卸压槽井筒而言,地下水水位下降20 m(图 4a)时,埋深158~174 m砂层局部出现达到极限应变值的单元,但井筒未出现达到极限应变的单元;说明砂层出现局部破坏,但井筒是安全的。地下水水位下降27 m(图 4b)时,达到土体极限应变区域不断扩大,并围绕井筒四周连接成片,但井筒仍未出现达到极限应变的单元。地下水水位降低38 m(图 4c)时,深度182~183 m井筒位置出现极限应变贯通区,数值计算不收敛,开设泄压槽井筒发生破坏。

|
| a. 水位下降20 m;b. 水位下降27 m。 图 3 不同水位下降无卸压槽井筒极限剪应变云图 Fig. 3 Cloud diagram of the ultimate shear strain of shaft with stress-relief groove and soil under different groundwater drop levels |
|
|

|
| a. 水位下降20 m;b. 水位下降27 m;c.水位下降38 m。 图 4 不同水位下降带卸压槽井筒极限剪应变云图 Fig. 4 Cloud diagram of the ultimate shear strain of shaft with stress-relief groove and soil under different groundwater drop levels |
|
|
对比发现,带卸压槽井筒与无卸压槽井筒极限应变发展规律为:地下水水位下降20 m时,带卸压槽井筒与无卸压槽井筒在158~174 m砂层达到极限应变区域。地下水水位下降27 m时,带卸压槽井筒与无卸压槽井筒极限应变区域出现差异:无卸压槽井筒不仅在土体区域形成极限应变贯通带,在井筒深度181~182 m也形成极限应变贯通带,井筒发生破坏;带卸压槽井筒仅在土体部分形成极限应变贯通区,井筒内未达到极限应变单元。地下水水位下降38 m时,带卸压槽井筒发生破坏。
从井筒破坏时的极限应变贯通区看,带卸压槽井筒和无卸压槽井筒极限应变贯通区高度都是1 m,但位置不同。无泄压槽井筒破坏深度在181~182 m,带卸压槽井筒则在182~183 m。井筒周围土体极限应变贯通区分为上下2部分:带泄压槽井筒上下2部分土体的极限应变贯通区最终发展为一个大的贯通区;无泄压槽井筒上下2部分土体的极限应变贯通区各自发展成片,最终没有联通为一个大的贯通区。
3.2.2 井筒竖向应力图 5为井筒承受的竖向应力随深度变化曲线。地下水水位降低27 m,无卸压槽井筒181~182 m发生破坏,破坏时最大竖向应力为40 MPa;此时带卸压槽井筒最大竖向应力仅为30 MPa,未达到C40混凝土强度极限40 MPa,说明带卸压槽井筒未发生破坏。相同埋深条件下,带卸压槽井筒竖向应力小于无卸压槽井筒的竖向应力,说明卸压槽发挥了井筒应力释放作用。极限状态下,带卸压槽井筒竖向应力和无卸压槽井筒竖向应力整体分布规律相同,最大竖向应力都是40 MPa,带泄压槽井筒最大竖向应力出现在182~183 m,无泄压槽井筒出现在在181~182 m,最大竖向应力的区域与井筒极限应变贯通区范围一致。

|
| 图 5 井筒竖向应力随井筒深度变化曲线 Fig. 5 Relation between the vertical stress and depth of shaft |
|
|
图 6为不同地下水水位下降值对应的卸压槽应力云图。泄压槽竖向应力随地下水水位降低不断增大。从应力转移规律看,水平方向主要从井筒靠近土体一侧向井筒内侧传递,随后向卸压槽转移,竖直方向上由上部至下部逐渐增大。地下水水位降低10 m,卸压槽底部承受最大竖向应力为7 MPa,并由外侧向内侧、下部向上部逐渐减小;水位降低20、27、31 m时,应力分布规律与水位降低10 m相似;水位降低38 m,卸压槽底部承受最大压应力为17 MPa。

|
| a. 水位下降27 m;b. 水位下降31 m;c. 水位下降38 m。 图 6 不同水位下降卸压槽应力云图 Fig. 6 Cloud diagram of vertical stress of stress-relief groove under different groundwater drop levels |
|
|
图 7为不同地下水水位下降值对应的卸压槽竖向压缩量云图。地下水水位下降27、31、38 m,卸压槽最大压缩量分别为27、37、113 mm。卸压槽的极限压缩量为自身高度的25%~30%,即112~135 mm,数值计算水位下降38 m时井筒破坏,对应的泄压槽压缩量为113 mm,已经是卸压槽压缩量的极限值范围,进一步说明了计算的可靠性。

|
| a. 水位下降27 m;b. 水位下降31 m;c. 水位下降38 m。 图 7 不同水头下降卸压槽竖向压缩量云图 Fig. 7 Cloud diagram of vertical compression of stress-relief groove under different groundwater drop levels |
|
|
泄压槽最优位置是井筒破坏时对应的地下水水位下降最大值。泄压槽位置分别为157.6、156.6、155.6、154.6 m时,破坏时对应的水位下降值分别为38、39、37、37 m,最佳的泄压槽开设位置为深度156.6 m。
4 泄压槽变形量监测数据分析图 8为井筒泄压槽实际监测的变形量随时间变化曲线。从图 8可以看出,从2005到2017年,卸压槽变形量总体呈增大趋势,截止到2017年压槽最大变形量3.6 mm,远未达到卸压木高度的25%临界值,井筒处于安全状态。从观测孔的地下水水位看,地下水水位从2005年的30 m降为2017年的10 m,水位共计下降了20 m。数值计算得出的卸压槽压缩量与实际监测井筒卸压槽压缩量的3.6 mm较为吻合,验证了数值极限应变方法的可靠性。

|
| 图 8 卸压槽变形量随时间变化曲线 Fig. 8 Deformation curve of stress-relief groove with time |
|
|
1) 将数值极限应变方法用于分析深厚松散地层中混凝土井筒应变值变化情况,提出混凝土井筒整体破坏的数值极限应变判据,当井筒中达到极限应变的单元环向贯通,井筒出现贯通性裂缝,且数值计算不收敛时,认定井筒发生破坏。
2) 从极限应变发展过程看,井筒周围砂层先于井筒出现达到极限应变的单元,并首先围绕井筒四周贯通,随后井筒外壁出现达到极限应变的单元,并逐渐向内壁发展,最终井筒出现贯通性裂缝。井筒破坏后,土体从井筒破坏位置涌出,此时砂土真正发生破坏。
3) 数值极限应变方法对混凝土井筒破坏分析表明,地下水水位下降27 m,无泄压槽井筒在深度181~182 m发生破坏;地下水水位下降38 m,带卸压槽井筒在深度182~183 m发生破坏。计算井筒最优泄压槽位置为深度156.6 m。
4) 本文将数值极限应变方法应用于混凝土井筒破坏预测中,初步计算给出的井筒破坏区域与已发生破坏井筒的位置比较吻合,但地下水水位下降38 m井筒发生破坏这一结论是否准确目前还无法验证。这是初步的探索,还需要继续深入研究。
| [1] |
陈湘生. 华东地区立井井壁破坏原因浅析[J]. 建井技术, 1997, 18(6): 1-3. Chen Xiangsheng. Analysis on the Causes of Shaft Wall Destruction in East China[J]. Mine Construction Technology, 1997, 18(6): 1-3. |
| [2] |
吕恒林, 崔广心. 深厚表土层中井壁结构破坏的力学机理[J]. 中国矿业大学学报, 1999, 28(6): 539-543. Lü Henling, Cui Guangxin. Mechanical Mechanism of Shaft Wall Structure Failure in Deep Topsoil[J]. Journal of China University of Mining and Technology, 1999, 28(6): 539-543. DOI:10.3321/j.issn:1000-1964.1999.06.005 |
| [3] |
张黎明, 杨建华, 张广学, 等. 深厚表土层井筒破坏预防性治理技术[J]. 煤炭科学科技, 2008, 36(4): 46-49. Zhang Liming, Yang Jianhua, Zhang Guangxue, et al. Preventive Control Technology for Mine Shaft Damage in Deep Overburden[J]. Coal Science and Technology, 2008, 36(4): 46-49. |
| [4] |
毕思文. 徐淮地区煤矿竖井变形破坏特征与机理探讨[J]. 建井技术, 1997, 18(3): 37-39. Bi Siwen. Discussion on Deformation and Failure Characteristics and Mechanism of Coal Mine Shaft in Xuhuai Area[J]. Mine Construction Technology, 1997, 18(3): 37-39. |
| [5] |
许延春, 耿得庸, 官云章, 等. 深厚含水松散层的工程特性及其在矿区的应用[M]. 北京: 煤炭工业出版社, 2003. Xu Yanchun, Geng Deyong, Guan Yunzhang, et al. Engineering Characteristics of Deep Water-Bearing Loose Layer and Its Application in Mining Area[M]. Beijing: Coal Industry Press, 2003. |
| [6] |
杨维好, 李峰, 王宗胜, 等. 冲积层疏排水与注浆过程中井壁应变变化规律实测研究[J]. 岩石力学与工程学报, 2007, 26(1): 2713-2717. Yang Weihao, Li Feng, Wang Zongsheng, et al. Field Measurements for Strains in Shaft Lining in Alluvium During Drainage and Grouting[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(1): 2713-2717. |
| [7] |
经来旺, 张天勇, 徐辉东, 等. 矿区表土疏水沉降机理及其与井壁破裂的关系[J]. 煤田地质与勘探, 2003, 33(3): 61-64. Jing Laiwang, Zhang Tianyong, Xu Huidong, et al. Relation Between the Seepage Sedimentation Mechanism of Soil in Mining Area and Shaft Rupture[J]. Coal Geology & Exploration, 2003, 33(3): 61-64. |
| [8] |
李文平. 深部土层失水变形时土与井壁相互作用试验与理论研究[J]. 岩土工程学报, 2000, 22(4): 475-480. Li Wenping. Testing and Theoretical Studies on the Interaction Between Soil and Shaft Wall During Deep Soil Compression Due to Losing Water[J]. Chinese Journal of Geotechnical Engineering, 2000, 22(4): 475-480. DOI:10.3321/j.issn:1000-4548.2000.04.018 |
| [9] |
彭向和, 杨春和. 复杂加载史下混凝土的损伤及其描述[J]. 岩石力学与工程学报, 2000, 19(2): 157-164. Peng Xianghe, Yang Chunhe. The Damage and Its Description of Concrete Under Complex Loading History[J]. Chinese Journal of Rock Mechanics and Engineering, 2000, 19(2): 157-164. |
| [10] |
张楠, 程桦, 荣传新, 等. 冻结井高强混凝土损伤演化与渗透性关系[J]. 硅酸盐学报, 2018, 46(10): 1366-1372. Zhang Nan, Cheng Hua, Rong Chuanxin, et al. Relation Between Damage Evolution and Permeability of High-Strength Concrete of Freezing Shaft Lining[J]. Journal of the Chinese Ceramic Society, 2018, 46(10): 1366-1372. |
| [11] |
荣传新, 王秀喜, 蔡海兵, 等. 基于流固耦合理论的煤矿立井井壁突水机理分析[J]. 煤炭学报, 2011, 36(12): 1366-1372. Rong Chuanxin, Wang Xiuxi, Cai Haibing, et al. Analysis of Shaft Water Irruption Mechanismin Coal Mine Based on Fluid-Solid Coupling Theory[J]. Journal of China Coal Society, 2011, 36(12): 1366-1372. |
| [12] |
吴月秀, 刘滨, 远洋, 等. 复杂荷载作用下冻结凿井井壁损伤应力分析[J]. 金属矿山, 2010(8): 42-45, 78. Wu Yuexiu, Liu Bin, Yuan Yang, et al. Stress Analysis on Freeze Sinking Sidewall's Damage Under Complicated Load[J]. Mental Mine, 2010(8): 42-45, 78. |
| [13] |
许良发. 深厚表土冻结井壁结构破裂机理及修复技术研究[J]. 煤炭技术, 2016, 35(12): 98-101. Xu Liangfa. Fracture Mechanism and Remediation Technology of Frozen Shaft Lining in Thick Top Soil[J]. Coal Technology, 2016, 35(12): 98-101. |
| [14] |
王英杰, 赵光思, 董国庆. 立井井壁破裂前后应变演化分析[J]. 煤炭工程, 2013, 45(4): 74-76. Wang Yingjie, Zhao Guangsi, Dong Guoqing. Analysis on Stress Evolution Before and After Mine Shaft Liner Broken[J]. Coal Engineering, 2013, 45(4): 74-76. |
| [15] |
葛晓光. 地面与破壁注浆治理井壁破裂灾害的工程分析[J]. 煤炭学报, 2002, 27(1): 41-44. Ge Xiaoguang. Engineering Properties of Two Grouting Techniques in Mending Shaft-Lining[J]. Journal of China Coal Society, 2002, 27(1): 41-44. |
| [16] |
琚宜文, 刘宏伟, 王桂梁, 等. 卸压套壁法加固井壁的力学机理与工程应用[J]. 岩石力学与工程学报, 2003, 22(5): 773-777. Ju Yiwen, Liu Hongwei, Wang Guiliang, et al. Mechanical Mechanism of Reinforcing Shaft-Wall with Pressure Release and Casing-Wall Method and Its Engineering Application[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(5): 773-777. |
| [17] |
郑颖人. 岩土数值极限分析方法的发展与应用[J]. 岩石力学与工程学报, 2012, 31(7): 1297-1316. Zheng Yingren. Development and Application of Numerical Limit Analysis for Materials[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(7): 1297-1316. |
| [18] |
郑颖人, 孔亮. 岩土塑性力学[M]. 北京: 中国建筑工业出版社, 2010. Zheng Yingren, Kong Liang. Geotechnical Plastic Mechanics[M]. Beijing: China Construction Press, 2010. |
| [19] |
阿比尔的, 冯夏庭, 郑颖人. 岩土类材料应变分析与基于极限应变判据的极限分析[J]. 岩石力学与工程学报, 2015, 34(8): 1552-1560. Abi Erdi, Feng Xiating, Zheng Yingren, et al. Strain Analysis and Numerical Analysis Based on Limit Strain for Geomaterials[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(8): 1552-1560. |
| [20] |
丛宇, 孔亮, 郑颖人, 等. 混凝土材料剪切强度的试验研究[J]. 混凝土, 2015, 34(5): 40-45. Cong Yu, Kong liang, Zheng Yingren, et al. Experimental Study on Shear Strength of Concrete[J]. Concrete, 2015, 34(5): 40-45. |
| [21] |
混凝土结构设计规范: GB 50010-2010[S]. 北京: 中国建筑工业出版社, 2011. Design Code for Concrete Structures: GB 50010-2010[S]. Beijing: China Industry Publishing House, 2011. |





