2. 华东建筑设计研究院有限公司上海地下空间与工程设计研究院, 上海 200011
2. Shanghai Underground Space Engineering Design & Research Institute, East China Architecture Design & Research Institute Co., Ltd., Shanghai 200011, China
0 引言
振动沉桩工艺是指使用振动锤在桩顶施加周期动荷载而完成沉桩,至今已有80多年应用的历史[1]。常规振动沉桩工艺由于振动强烈、噪音大等缺点,在城市或者特殊条件下应用受到严格限制。近年来,随着振动沉桩工艺不断发展,一种高工效的新型振动沉桩工艺——免共振沉桩开始在上海主城区得到应用[2-4]。免共振沉桩同样在桩顶施加周期动荷载,但所用加载设备为免共振锤,采用高振动频率且在启停阶段无振动输出以避免共振现象,进而对土体振动影响大为降低[2-5]。但是,随着免共振沉桩逐步在紧邻建筑物、地铁等复杂敏感环境中应用[2-4],如在国家会展中心(上海)的双层改造工程中进行室内沉桩,且临近地铁、燃气管道等敏感建(构)筑物[4],其所产生的地表振动影响尚需进一步研究。
采用现场测试研究免共振沉桩对地表振动影响是一种直接且可靠的方法,但其成本较高且不易重复。除此之外,数值模拟也是一种经济可行的方法。在数值模拟中,可直接在桩身施加一定频率的周期动荷载,无需经历启停阶段。因此,免共振沉桩与常规振动沉桩在数值模拟中并没有区别。在振动沉桩过程中,桩土相互作用也与沉桩过程相关。目前已有不少学者进行了连续振动沉桩的数值模拟,主要运用有限元法建立相应的数值模型[6-10],还有学者采用物质点法[11]以及离散元法[12]进行数值模拟。也有学者[13-14]采用有限差分法进行振动沉桩的数值研究,但其通常将模型桩预置在土体的特定深度,模拟贯入深度较小,鲜有学者采用有限差分法进行连续振动沉桩模拟。连续振动沉桩数值模拟属于动力分析,当模型桩使用线弹性本构时,其弹性模量过大(如常规钢管桩206 GPa)将导致数值计算花费较长时间[15]。实际沉桩过程中桩的变形较小,为避开模型桩弹性模量过大对计算时间的影响,学者们在数值模拟中通常将模型桩设为刚体[6-10]。基于有限差分法的FLAC3D数值软件有较好的动力分析功能,可用于连续振动沉桩模拟;但FLAC3D没有刚体单元,其“动态多步”法在一定程度上能缓解模型中部分单元弹性模量过大对计算时间的影响[16],然而在建模过程中发现“动态多步”法的改善效果有限。
基于此,本文尝试在有限差分软件FLAC3D中,采用“密度放大法”消除模型桩弹性模量过大对连续振动沉桩数值计算效率的影响,并对文献[4]中免共振沉桩的地表振动现场测试进行模拟和分析,以研究激振力幅值和振动频率这两个施工参数对地表振动特性的影响。
1 连续沉桩数值模型文献[4]中免共振沉桩的地表振动现场测试位于上海地区的国家会展中心(上海)室内,为非原位试桩。试桩为薄壁开口钢管桩(外径为700 mm,壁厚为14 mm,桩长为60 m),采用免共振锤ICE-70RF施工,监测了距沉桩中心水平距离1.0、5.0、11.5、12.5、24.5和25.0 m处的地表振动。本文将对文献[4]中的现场测试进行模拟。
1.1 几何模型为合理模拟桩体贯入土体的过程,Henke等[6]和肖勇杰等[8]采用zipper-type建模技术在有限元软件ABAQUS中实现了开口管桩的连续振动沉桩数值模拟。本文在有限差分软件FLAC3D中也将使用该技术,即在土体中预先设置直径1 mm的辅助管(图 1),沉桩时辅助管固定不动,管桩桩壁沿着辅助管贯入土体,且同时生成相应的桩土接触。

|
| 图 1 轴对称数值模型 Fig. 1 Axisymmetric numerical model |
|
|
根据开口管桩沉桩的轴对称特性,在垂直纸面方向(y向)上只设置一个单元并限制该方向的位移,建立相应的轴对称模型,轴对称线与管桩中心轴线重合。参照文献[4]中的薄壁开口钢管桩,已知模型桩外径D为700 mm,壁厚为14 mm。由于动力计算十分耗时,本文模型桩长度取5.0 m、沉桩深度为7.0倍桩径(7.0D,下文沉桩深度和水平距离均取桩径倍数进行归一化处理)。为减弱动力分析中地基模型边界处反射波的影响,除设置较大地基模型尺寸外,在FLAC3D中还可施加静态边界或自由场边界。然而,在动力计算过程中,静态边界和自由场边界的初始反力均保持不变[16],模型桩的挤土效应将导致边界处无法维持力学平衡。因此,本文设置较大地基模型尺寸以减弱边界处反射波的影响,即x方向设置为30.0 m、z方向设置为20.0 m(图 1)。
1.2 模型参数在连续振动沉桩数值模拟中,考虑动孔压积累和消散还较困难,学者们通常采用不排水分析法[7-8]。根据文献[4]中现场测试所在场地的土层特点,笔者也采用不排水分析法建立饱和黏土均质土体模型。所有单元均为实体单元,土体本构模型选用Mohr-Coulomb弹塑性模型,模型桩和辅助管则采用线弹性模型,参数见表 1。
| 材料 | 本构模型 | ρ/(kg/m3) | E/GPa | υ | c/kPa | φ/(°) |
| 土体 | Mohr-Coulomb | 1 800 | 0.01 | 0.49 | 21 | 0 |
| 模型桩 | 线弹性 | 7 850 | 206 | 0.26 | - | - |
| 辅助管 | 线弹性 | 7 850 | 206 | 0.26 | - | - |
| 注:ρ. 密度;E. 弹性模量;υ. 泊松比;c. 黏聚力;φ. 内摩擦角。 | ||||||
关于接触面参数的选取,法向和切向刚度通过参数试算获得。Henke等[6]和肖勇杰等[8]分别将桩土接触的摩擦角δ设为10°和14°,考虑到免共振沉桩效率高[4],本文取较小值10°,而辅助管与土接触的摩擦角则根据zipper-type建模技术[6-8]的特点设为0°,参数见表 2。
| 类型 | kn/(GPa·m) | ks/(GPa·m) | δ/(°) |
| 模型桩与土 | 4 | 0.04 | 10 |
| 辅助管与土 | 8 | 8.00 | 0 |
| 注:kn. 法向刚度;ks. 切向刚度。 | |||
荷载参数基于文献[4]中免共振锤ICE-70RF选取,沉桩过程中作用在桩身上的荷载Fp为
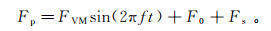 (1)
(1) 式中: FVM为激振力幅值,取固定值300 kN;f为免共振锤工作频率,取固定值33.3 Hz;t为沉桩时间,s;F0为静荷载,取模型桩自重7.5 kN,为固定值;Fs为沉桩过程中土体总阻力,kN,根据桩土接触力大小实时更新。
沉桩过程中,管桩变形很小,可视为刚性。因此,模型桩的运动为竖向刚体运动,可采用加速度动荷载施加方法,即模型桩的所有节点施加相同的加速度a:
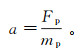 (2)
(2) 式中,mp为模型桩质量,取固定值750 kg。
Kuhlemyer等[17]认为,要想精确描述模型中波的传播,网格尺寸Δl应小于输入波形最高频率对应波长的1/8~1/10,即Δl ≤ (1/8~1/10) λ,其中λ为最高频率对应的波长。本文将免共振锤的工作频率视为最高频率,由公式(3)[16, 18]通过土体参数计算得到波长λ为1.30 m,Δl取1/8波长,即0.16 m。
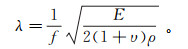 (3)
(3) 为合理反映桩周土体变形,沉桩中心的近场土体网格需进行相应加密。同时,模型y向单元尺寸根据试算取0.70 m。由此,土体模型中土体单元最小尺寸约为0.03 m (x向) ×0.16 m (z向),最大尺寸约为0.16 m (x向) ×0.16 m (z向)。最终,整个数值模型共有27 410个单元、55 864个节点,数值模型网格划分如图 1所示。阻尼采用局部阻尼形式,考虑到免共振锤工作频率高达33.3 Hz,土体临界阻尼取10%。
2 计算效率提高方法 2.1 动力时步FLAC3D采用显式差分法求解微分方程,在每一时步中完成运动方程和本构方程求解,时步越小意味着数值模拟所需的计算时间就越长[18]。在动力分析中,其动力时步需遍历所有单元后取最小值。动力时步将由几何尺寸较小和弹性模量较大的单元来确定,计算公式[16]为:
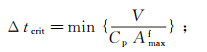 (4)
(4) 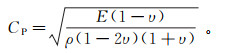 (5)
(5) 式中: Δtcrit为动力临界时步,s;CP为压缩波波速,m/s;V为四面体子单元体积,m3;Amaxf为与四面体子单元相关的最大表面积,m2;min{}表示遍历所有单元,也包括接触单元。
由于本文数值模型中模型桩和辅助管尺寸小且弹性模量过大,导致动力时步低至约2.52×10-8 s。若不采取相应的处理方法,计算时间将十分漫长。
2.2 动态多步法针对动力分析中部分单元弹性模量过大,影响计算效率的问题,FLAC3D提供了动态多步法来减少计算所需的时间[16]。为探讨动态多步法的改善效果,笔者引入FLAC3D手册中一个较简单的动力分析算例[16]进行不同弹性模量的计算效率比较研究。算例的几何尺寸如图 2所示,所有单元各坐标轴方向的尺寸均为0.5 m,总单元数为2 660,其中墙体单元数为340。土体和墙体均采用线弹性模型,弹性模量分别为20和300 MPa,泊松比均为0.2。在研究过程中,逐渐提高墙体弹性模量EW,获得动力时步比td/td0、计算时间比tcal/tcal0和计算效率提高系数toff/ton的变化规律,其中下标off表示未采用动态多步法,下标on表示采用动态多步法。动力荷载时长为1.0 s。所用计算机处理器为Intel(R) Xeon(R) CPU E3-1230 V2 @3.30GHz,4核CPU,8个逻辑处理器。
如图 3所示:随着墙体弹性模量比EW/EW0的增大,td/td0呈线性减小的规律;无论是否采用动态多步法,tcal/tcal0均随EW/EW0快速增大,但采用动态多步法时tcal/tcal0始终较不采用动态多步法小;当EW/EW0增加到一定程度时,toff/ton基本保持不变。以上结果表明,当弹性模量过大时,动态多步法的toff/ton基本不超过5,说明对于连续振动沉桩而言,计算耗时可能仍较长。

|
| 图 3 动态多步法效果比较 Fig. 3 Comparison on the effective of dynamic multi-stepping |
|
|
为进一步提高计算效率,由式(4)和式(5)可知,当模型桩密度放大足够倍数后(本文取106),CP将急剧减小,相应的动力临界时步将大幅地增大,从而数值模型的动力时步将由弹性模量较小的土体单元决定(本文动力时步由2.52×10-8 s降为1.77×10-5 s)。在模型桩密度发生改变后,其质量也将变化,等效于将式(2)中的mp乘以106。为保证密度放大前后桩身所有节点的加速度保持不变,将式(2)中Fp也乘以106。
当模型桩在密度放大前后的加速度保持不变时,其运动特性不会受到密度改变的影响。接触面建立在模型桩表面上,接触面的速度变化也不会受密度改变的影响。因此,接触面节点和目标面之间的绝对法向刺入量和相对剪切速度不会受密度改变的影响,进而不会影响桩土相互作用。对于辅助管的密度,也需放大同样的倍数。由于在沉桩过程中辅助管始终被固定,密度放大法则不会影响辅助管的运动特性和其与土体之间的相互作用。
2.4 方法对比为进一步验证密度放大法,进行了沉桩深度仅为0.1D的试算,分为不做处理、采用动态多步法和采用密度放大法3种工况。数值计算所耗费的时间tcal和地表距沉桩中心水平距离R = 1.5D的z向振动速度vz时程曲线如图 4所示,其中所用计算机处理器为Intel(R) Core(TM) i7-5960XCPU @3.00GHz,8核CPU,16个逻辑处理器。

|
| 图 4 沉桩深度0.1D时不同方法的计算时间和z向振动速度比较 Fig. 4 Comparison on the tcal and the vz by different methods with a penetration depth of 0.1D |
|
|
如图 4所示, 在沉桩深度达到0.1D时,不做处理的工况所耗费的计算时间约为19.1 h,采用动态多步法的工况所耗费的计算时间约为15.2 h,而采用密度放大法所耗费的计算时间仅为0.2 h。由此可以看出:密度放大法能极大地减小连续振动沉桩模型的计算时间,计算效率较不做处理提高95.5倍左右;而动态多步法对计算效率的改善则非常有限,计算效率较不做处理仅提高约1.3倍。或许这也是鲜有学者采用有限差分软件FLAC3D模拟连续振动沉桩的原因之一。
同时,由图 4可以看出,采用动态多步法对地表振动曲线几乎没有影响,而密度放大法则主要在数值上有较小影响,波动规律几乎与不做处理的工况重合。为减小连续振动沉桩的数值计算时间,学者们[6-10]大多也假设模型桩为刚体。为有效缩短FLAC3D中连续振动沉桩模型的数值计算时间,可认为密度放大法能合理反映沉桩过程中的地表振动特征。采用密度放大法后,模拟沉桩7.0D所用计算时间约为12.0 h。
3 数值结果分析 3.1 地表振动时程曲线为反映连续沉桩过程中地表振动特征,图 5给出了地表距沉桩中心水平距离R = 1.5D和7.0D处的x和z方向振动速度时程曲线。

|
| a. R=1.5D;b. R=7.0D。 图 5 地表振动速度时程曲线 Fig. 5 Time-history curve of ground vibration velocity |
|
|
由图 5可知,地表振动速度在沉桩初期出现了峰值,振动速度在后续阶段明显小于峰值,且幅值大小基本不变。振动速度峰值可反映沉桩过程对地表振动影响强烈程度,该值也可称为土体峰值质点速度(peak particle velocity,PPV)。根据Athanaso- polous等[19]的总结,学者们选取PPV值的方法并不统一,本文依据《建筑工程容许振动标准》(GB 50868—2013)[20]取沉桩过程中径向、切向和竖向振动速度的最大值作为PPV。因此,水平距离R=1.5D和7.0D处的PPV分别为25.4和8.6 mm/s。
3.2 数值模拟与现场测试值比较为验证数值模型的模拟效果,图 6给出了不同归一化水平距离R/D处PPV的数值模拟与现场测试[4]对比曲线。

|
| 图 6 数值模拟与现场测试对比 Fig. 6 Comparison between numerical simulation and field test |
|
|
由图 6可以看出,数值结果较好地模拟了免共振沉桩时在地表所产生的PPV随水平距离增大而快速衰减的现象。同时也可发现,数值结果在近场处大于现场测试值。数值上的差异主要可从以下两点解释:1)文献[4]中在现场沉桩时,提前挖除了沉桩中心直径约0.7 m的表层土体,这在一定程度上减弱了地表的振动影响;2)本文数值模拟的土体本构模型还比较简单,未能考虑实际沉桩过程中动孔压生成对振动能量耗散的影响。但总体上而言,本文数值模拟结果能较好反映免共振沉桩对地表振动的影响,可进一步分析沉桩过程地表振动的影响因素。
3.3 沉桩过程中地表振动特性肖勇杰等[8]的研究结果表明,当达到临界沉桩深度时,地表振动影响最为强烈。为此,在达到不同沉桩深度时,进行相应PPV取值,得到不同归一化水平距离R/D处的PPV随归一化沉桩深度L/D变化曲线(图 7)。

|
| 图 7 PPV与归一化沉桩深度变化曲线 Fig. 7 Curves of PPV with varying normalized penetration depth |
|
|
如图 7所示:不同R/D处的PPV在沉桩初期随着L/D增加而增大,但当达到一定深度后不再增大,达到PPV最值的深度即为临界沉桩深度Lcrit/D;不同R/D处的Lcrit/D不同,其基本上随着R/D增大而增大;当沉桩深度达到7.0D时,R/D越小其PPV越大,与图 6中的规律相符。
为更直观反映Lcrit/D在地表不同R/D处的变化规律,图 8绘制了相应的曲线。同时包括肖勇杰等[8]的开口管桩高频振动沉桩数值模拟、Thandavamoorhty[21]的开口管桩锤击沉桩现场测试、以及Khoubani等[22]的闭口实心桩锤击沉桩数值模拟。

|
| 图 8 地表的归一化临界沉桩深度曲线 Fig. 8 Curves of normalized critical penetration depth at ground surface |
|
|
由图 8可发现,Lcrit/D基本随R/D增大而增加,但是增加幅度越来越小。肖勇杰等[8]的数值模拟结果也基本呈现相同的变化规律,数值上的差异可能和ABAQUS中所采用的任意拉格朗日欧拉(ALE) 自适应网格划分技术有关。为减缓沉桩过程桩周土体网格畸变,采用ALE技术可对土体网格进行重新划分和传递计算参数[23],此过程可能对桩周土体动力响应有所影响。由图 8还可发现,锤击沉桩的现场测试[21]和数值模拟[22]结果也存在使地表PPV达到最大值的Lcrit/D,在近场同样表现出Lcrit/D随R/D增大的趋势。此外,本文数值模拟的地表临界沉桩深度小于4.0D,说明本文数值模拟沉桩深度取7.0D是合理的,可模拟免共振沉桩过程对地表的振动影响。
4 影响地表振动特性的因素分析 4.1 激振力幅值为分析激振力幅值对地表振动特性的影响规律,分别将激振力幅值FVM设置为300、360和420 kN,振动频率仍为33.3 Hz,得到地表PPV和Lcrit/D曲线(图 9)。

|
| 图 9 激振力幅值对PPV和归一化临界沉桩深度的影响 Fig. 9 Effect of PPV and Lcrit/D from different FVM |
|
|
由图 9可以看出,激振力幅值对地表PPV的大小有一定影响,但对衰减规律没有明显影响。在近场(水平距离R小于5.0D),地表PPV总体上随着激振力幅值增大而明显增大;在远场,地表PPV变化不明显。同时也可以发现,激振力幅值对Lcrit/D的影响不明显。肖勇杰等[8]的结果则也表明激振力幅值对Lcrit/D的影响不明显。
4.2 振动频率在如振动沉桩等施工引起的地表振动传播过程中,振源频率越高,则其振动衰减得越快。而免共振沉桩所谓的“免共振”特性,除与免共振锤可不停机调偏心矩的特点有关,也与免共振锤能维持高工作频率的性能相关[4]。为比较不同振动频率对地表PPV和Lcrit/D的影响,图 10给出了不同振动频率的计算结果,其中激振力幅值为420 kN。

|
| 图 10 振动频率对PPV和归一化临界沉桩深度的影响 Fig. 10 Effect of PPV and Lcrit/D from different frequency |
|
|
由图 10可知,不同振动频率的地表PPV衰减规律几乎相同,而振动频率对近场水平距离(R小于5.0D)地表PPV大小改变较为明显。以水平距离R=1.5D为例,当振动频率由33.3 Hz增大为43.3 Hz时,地表PPV则从39.7 mm/s降为25.5 mm/s。振动频率对Lcrit/D的影响主要在水平距离10.0D以外远场较为明显,当振动频率由23.3 Hz增大为33.3 Hz或43.3 Hz时,Lcrit/D明显减小。
5 结论与建议1) 模型桩弹性模量过大,极大地增加有限差分软件FLAC3D中连续振动沉桩模拟的计算时间。在沉桩深度为0.1D时,不做处理所需计算时间为19.1 h,动态多步法耗时达15.1 h,后者较前者计算效率提高约1.3倍;而密度放大法只需0.2 h,较不做处理计算效率提高达95.5倍,且对地表振动响应的影响很小。采用密度放大法后,模拟沉桩7.0D所用计算时间为12.0 h左右。
2) 本文连续振动沉桩数值模型能较好模拟免共振沉桩对地表的振动影响,数值模拟结果在近场较大于现场测试值,但衰减规律基本相同。
3) 激振力幅值和振动频率这两个施工参数均对近场(R小于5.0D)地表振动有明显影响。临界沉桩深度与地表目标点的振动影响峰值对应,该深度随水平距离先增大后趋于稳定,且不超过4.0D。激振力幅值对临界沉桩深度影响不明显,振动频率对远场的临界沉桩深度有较明显影响。
在后期研究工作中,拟考虑动孔压生成与消散,建立连续振动沉桩的流固耦合数值模型。
| [1] |
Rajapakse R. Pile Design and Construction Rules of Thumb[M]. 2nd ed. Amsterdam: Elsevier, 2016: 286-290.
|
| [2] |
杨春柳. 钢管桩免共振施工对邻近地铁的振动影响试验研究[J]. 建筑施工, 2018, 40(9): 1655-1657. Yang Chunliu. Experimental Study on Vibration Effect of Steel Pipe Piles Resonance-Free Construction on Adjacent Metro[J]. Building Construction, 2018, 40(9): 1655-1657. |
| [3] |
李操, 张孟喜, 周蓉峰, 等. 免共振沉桩原位试验研究[J]. 长江科学院院报, 2020, 37(9): 122-127. Li Cao, Zhang Mengxi, Zhou Rongfeng, et al. In-Situ Test Study on Resonance-Free Pile[J]. Journal of Yangtze River Scientific Research Institute, 2020, 37(9): 122-127. |
| [4] |
王卫东, 魏家斌, 吴江斌, 等. 高频免共振法沉桩对周围土体影响的现场测试与分析[J]. 建筑结构学报, 2021, 42(4): 131-138. Wang Weidong, Wei Jiabin, Wu Jiangbin, et al. Field Test and Analysis on Surrounding Soil Effects of Pile Driving with High-Frequency and Resonance-Free Technology[J]. Journal of Building Structures, 2021, 42(4): 131-138. |
| [5] |
王进怀. 2.7高频液压振动沉拔桩锤[C]//中国土木工程学会土力学及基础工程学术委员会联合年会. 北京: 中国土木工程学会, 1998: 166-172. Wang Jinhuai. 2.7 High Frequency Hydraulic Vibration Sinking and Pulling Pile Hammer[C]//Joint Annual Meeting of the Soil Mechanics and Basic Engineering Academic Committee of China Civil Engineering Society. Beijing: China Civil Engineering Society, 1998: 166-172. |
| [6] |
Henke S, Grabe J. Numerical Investigation of Soil Plugging Inside Open-Ended Piles with Respect to the Installation Method[J]. Acta Geotechnica, 2008, 3(3): 215-223. DOI:10.1007/s11440-008-0079-7 |
| [7] |
Ekanayake S D, Liyanapathirana D S, Leo C J. Influence Zone Around a Closed-Ended Pile During Vibratory Driving[J]. Soil Dynamics and Earthquake Engineering, 2013, 53: 26-36. DOI:10.1016/j.soildyn.2013.06.005 |
| [8] |
肖勇杰, 陈福全, 林良庆. 灌注桩套管振动贯入引起的地面振动及隔振研究[J]. 岩土力学, 2017, 38(3): 705-713. Xiao Yongjie, Chen Fuquan, Lin Liangqing. Study of Ground Vibration and Vibration Isolation Due to Sleeve of Cast-in-Place Piles Installed by Vibratory Driving[J]. Rock and Soil Mechanics, 2017, 38(3): 705-713. |
| [9] |
Chen F Q, Lin Y Q, Dong Y Z, et al. Numerical Investigations of Soil Plugging Effect Inside Large-Diameter, Open-Ended Wind Turbine Monopiles Driven by Vibratory Hammers[J]. Marine Georesources and Geotechnology, 2020, 38(1): 83-96. DOI:10.1080/1064119X.2018.1553081 |
| [10] |
Daryaei R, Bakroon M, Aubram D, et al. Numerical Evaluation of the Soil Behavior During Pipe-Pile Installation Using Impact and Vibratory Driving in Sand[J]. Soil Dynamics and Earthquake Engineering, 2020, 134: 1-15. |
| [11] |
Galavi V, Beuth L, Coelho Z, et al. Numerical Simulation of Pile Installation in Saturated Sand Using Material Point Method[J]. Procedia Engineering, 2017, 175: 72-79. DOI:10.1016/j.proeng.2017.01.027 |
| [12] |
韩钧, 陈福全, 曹琪君. 高频液压振动沉桩的颗粒离散元分析[J]. 福州大学学报(自然科学版), 2011, 39(2): 287-292. Han Jun, Chen Fuquan, Cao Qijun. DEM Study on the Installation of a Pile Using the High Frequency Hydraulic Vibratory Hammer[J]. Journal of Fuzhou University (Natural Science Edition), 2011, 39(2): 287-292. |
| [13] |
Feng Z, Deschamps R J. A Study of the Factors Influencing the Penetration and Capacity of Vibratory Driven Piles[J]. Soils and Foundations, 2000, 40(3): 43-54. DOI:10.3208/sandf.40.3_43 |
| [14] |
陈福全, 雷金山, 汪金卫. 高频液压振动锤沉桩的打入性状分析[J]. 铁道科学与工程学报, 2009, 6(1): 41-47. Chen Fuquan, Lei Jinshan, Wang Jinwei. Penetration Behaviour Due to Vibratory Pile Driving Using the High Frequency Hydraulic Vibratory Hammer[J]. Journal of Railway Science and Engineering, 2009, 6(1): 41-47. DOI:10.3969/j.issn.1672-7029.2009.01.009 |
| [15] |
Rooz A F H, Hamidi A. A Numerical Model for Continuous Impact Pile Driving Using ALE Adaptive Mesh Method[J]. Soil Dynamic and Earthquake Engineering, 2019, 118: 134-143. DOI:10.1016/j.soildyn.2018.12.014 |
| [16] |
Itasca Consulting Group Inc. FLAC3D-Fast Lagrangian Analysis of Continua in Three-Dimensions, Ver. 6.0, User's Guide Manual[Z]. Minneapolis, 2019.
|
| [17] |
Kuhlemeyer R L, Lysmer J. Finite Element Method Accuracy for Wave Propagation Problems[J]. Journal of the Soil Mechanics and Foundations Division, 1973, 99(5): 421-427. DOI:10.1061/JSFEAQ.0001885 |
| [18] |
陈育民, 徐鼎平. FLAC/FLAC3D基础与工程实例[M]. 2版. 北京: 中国水利水电出版社, 2013: 225-234. Chen Yumin, Xu Dingping. FLAC/FLAC3D Foundation and Engineering Examples[M]. 2nd ed. Beijing: China Water and Power Press, 2013: 225-234. |
| [19] |
Athanasopolous G A, Pelekis P C. Ground Vibrations from Sheetpile Driving Urban Environment: Measurements, Analysis and Effects on Buildings and Occupants[J]. Soil Dynamic and Earthquake Engineering, 2000, 19: 371-387. DOI:10.1016/S0267-7261(00)00008-7 |
| [20] |
建筑工程容许振动标准: GB 50868-2013[S]. 北京: 中国计划出版社, 2013. Standard for Allowable Vibration of Building Engineering: GB 50868-2013[S]. Beijing: China Planning Press, 2013. |
| [21] |
Thandavamoorthy T. Piling in Fine and Medium Sand: A Case Study of Ground and Pile Vibration[J]. Soil Dynamic and Earthquake Engineering, 2004, 24(4): 295-304. DOI:10.1016/j.soildyn.2003.12.005 |
| [22] |
Khoubani A, Ahmadi M M. Numerical Study of Ground Vibration Due to Impact Pile Driving[J]. Geotechnical Engineering, 2012, 167(1): 28-29. |
| [23] |
Dassault Systemes Simulia. ABAQUS 2016 Analysis User's Manual, Ver. 6.16[Z]. Providence, 2016.
|



