2. 同济大学土木工程学院, 上海 200092
2. College of Civil Engineering, Tongji University, Shanghai 200092, China
0 引言
随着我国经济社会的深入发展,大量兴建于改革开放初期的建筑已经不能满足现阶段的使用要求,如工业厂房由于生产工艺的提升需要拆除重建以及老旧小区的拆迁等。老旧建筑拆除将产生大量的建筑垃圾,地上部分可以回收生产再生骨料加以利用,而对于埋在地下的桩基础则没有较好的处理措施。一般将旧桩留置在场地中,这会造成巨大的资源浪费,也将导致场地中旧桩越来越多,不仅使新基础难以找到有效的布桩方式,还可能阻碍新桩施工。移除旧桩不仅费用昂贵,且施工也相当困难,同时旧桩的移除对周围土体存在扰动,造成新桩表面摩阻力损失,使得新桩承载力达不到设计要求。对旧桩使用性能进行评价并通过合理设计,补充新桩,对其进行再利用,是处置残留旧桩行之有效的方法[1-3]。但新桩沉桩贯入过程中产生的挤土效应会使邻近既有桩产生附加变形和内力,严重时造成既有桩倾斜乃至折断,失去承载能力。因此确定新桩贯入挤土效应对既有桩的影响,并据此提出相应的防护措施对静压桩再利用的设计、施工具有重要的指导作用。
国内外学者已经对土体位移在既有桩中产生的内力与变形进行了研究。Leung等[4-6]用离心模型试验研究了基坑开挖引起的土体位移对邻近桩基弯矩、变形的影响。Poulos等[7-8]运用两阶段法分析了隧道、基坑开挖引起的邻近桩基弯矩和变形。但上述研究均未采用沉桩产生的挤土位移分布形式,因此未能考虑新桩沉桩挤土位移对邻近桩基的影响。对静压桩沉桩产生的挤土位移,国内外学者也进行了大量的研究。Sagaseta等[9-10]在圆孔扩张理论的基础上采用了源汇法,考虑地表自由边界的影响,得到了半无限体中的沉桩挤土位移。周火垚等[11]和张明义等[12]分别开展了静压沉桩的模型试验和现场试验,研究了沉桩时的挤土位移随深度和距桩轴不同距离的变化规律。罗战友等[13]基于应变路径法及源汇法理论,根据土体的固结度理论推导小应变条件下考虑超孔压消散的静压单桩挤土位移场的解析解。张亚国等[14]采用对软黏土具更好适用性的修正剑桥模型,推导了饱和软土中单桩挤土位移的解析式。以上研究均为在土体半无限空间中对沉桩挤土位移进行求解,但地基中残留的旧桩对新桩的贯入形成了非对称的位移边界条件,必然会对桩侧挤土位移场产生影响,而新桩贯入引起的挤土位移又会反作用于旧桩,这是一个相互作用的过程,目前对这一问题的研究还鲜有报道。因此需要进一步考虑旧桩存在时的静压桩沉桩挤土效应及其对旧桩内力和变形的影响。
本文首先基于半无限土体中的球孔扩张理论,推导新桩沉桩引起的土体位移场,然后将其作为已知条件施加于既有桩,基于Winkler地基模型求解新桩贯入挤土位移引起邻近既有桩的变形和内力变化。在此基础上,研究既有桩桩顶和桩端约束条件的影响。同时运用ABAQUS有限元软件,建立了邻近既有桩的静压桩贯入三维数值模型,运用位移贯入法实现新桩的连续贯入,与本文理论解答进行对比验证。最后分析了沉桩距离和新桩桩径对既有静压桩响应的影响,并提出降低新桩施工对既有桩影响的措施。
1 半无限土体中沉桩挤土位移解答 1.1 半无限土体中球孔扩张挤土位移半无限土体中的球孔扩张如图 1所示(y正方向为垂直纸面向外),其计算理论近年来得到了较快的发展。相比于无限土体中的球孔扩张,半无限土体中扩孔问题需要对水平地表边界条件进行应力修正。朱宁等[15]运用镜像法在假定土体饱和、均质、不可压缩、线弹性的前提下,给出了半无限土体中球孔扩张产生的位移及地表处产生的正应力和剪应力的解答,并运用应力函数对地表处的应力进行了修正,得到半无限土体中球孔扩张产生的位移ury和uzy分别为:
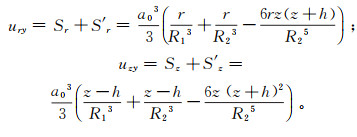 (1)
(1)
|
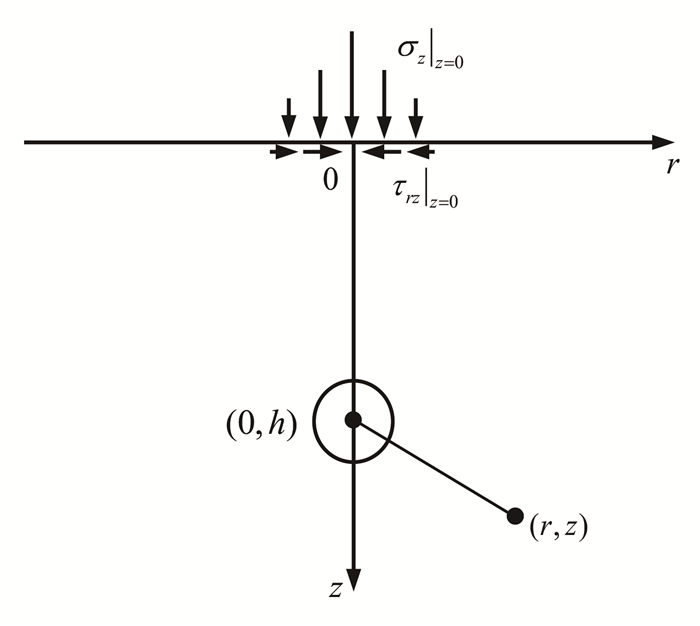
| σz和τrz分别为半无限土体中球孔扩张产生的正应力和剪应力。 图 1 半无限球孔扩张修正应力示意图 Fig. 1 Stress correction boundary for semi-infinite cavity expansion |
|
|
其中:
 (2)
(2) 式中:Sr、Sz分别为无限土体中球孔扩张产生的水平和竖直位移;Sr′、Sz′为修正剪应力和正应力产生的位移;a0为球孔半径。
1.2 半无限土体中沉桩挤土位移把半无限土体中静压沉桩任一微段的桩体等效为同体积的扩张球孔(图 2),可得
 (3)
(3)

|
| 图 2 沉桩等效示意图 Fig. 2 Euivalent of pile penetration by cavity expansion |
|
|
式中,d0为静压桩直径。则
 (4)
(4) 长度为L的桩体压入土体产生的挤土位移可以表示为对h进行从0到L的积分:
 (5)
(5) 式中:ur为水平挤土位移;uz为竖直挤土位移;ν为土体泊松比。
2 基于Winkler地基模型的既有桩响应基于Winkler地基模型的新桩贯入对既有桩影响的力学模型如图 3所示。新桩沉桩深度为L,直径为d0;既有桩入土深度为H,直径为D0。

|
| ks. 既有桩桩侧土体的基床反力模量;f(z). 土体作用于既有桩的反力。 图 3 新桩贯入引起既有桩响应力学模型 Fig. 3 Mechanical model of existing pile response caused by new pile penetration |
|
|
由式(5)可以得到静压沉桩引起的水平自由挤土位移,在既有桩的作用下,土体自由位移受到限制。取单位长度的既有桩作为研究对象,假定土体为连续均质弹性体,且土体和既有桩不发生分离,满足变形协调,设既有桩的最终桩身侧向位移为w(z),则ω(z)也即最终的挤土位移。由Winkler弹性地基模型将自由挤土位移转化为既有桩桩侧土压力,得到
 (6)
(6) 式中:p为单位长度既有桩任意深度上由于挤土位移作用引起的侧压力。采用Vesic[16]所提方法,将ks与周围土体的变形参数相联系,表达式为
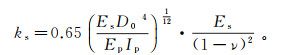 (7)
(7) 式中:Es为桩侧土体变形模量;Ep为既有桩桩身弹性模量;Ip为既有桩截面惯性矩。
将单位长度既有桩视为弹性地基梁,根据挠曲线方程可以得到沉桩挤土水平位移对既有桩侧向变形的控制方程:
 (8)
(8) 对既有桩:如果是纯摩擦桩,可以假设桩端为完全自由;如果是端承桩,可认为桩端完全固定。对既有桩桩顶,由于上部建筑在既有桩再利用时已经拆除,可以看作自由桩顶,假定桩顶处弯矩和剪应力为0。由于微分方程解法的限制,直接求解式(8)只适用于均质土体,对分层土体来说,需要利用差分法求解。
对既有桩为摩擦桩,考虑桩顶自由、桩端自由,可得刚度矩阵为
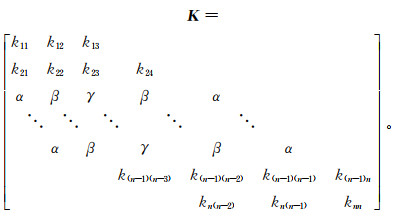 (9)
(9) 其中:
 (10)
(10) 对既有桩为端承桩,考虑桩顶自由、桩端固定,可得刚度矩阵为
 (11)
(11) 其中:
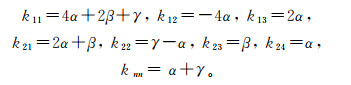
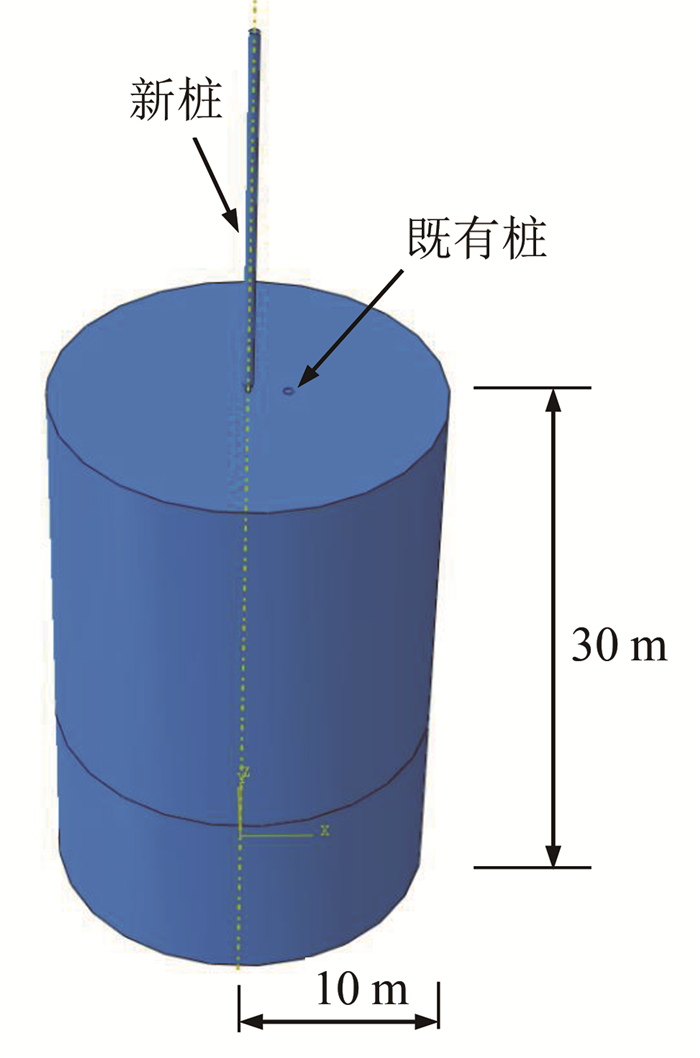
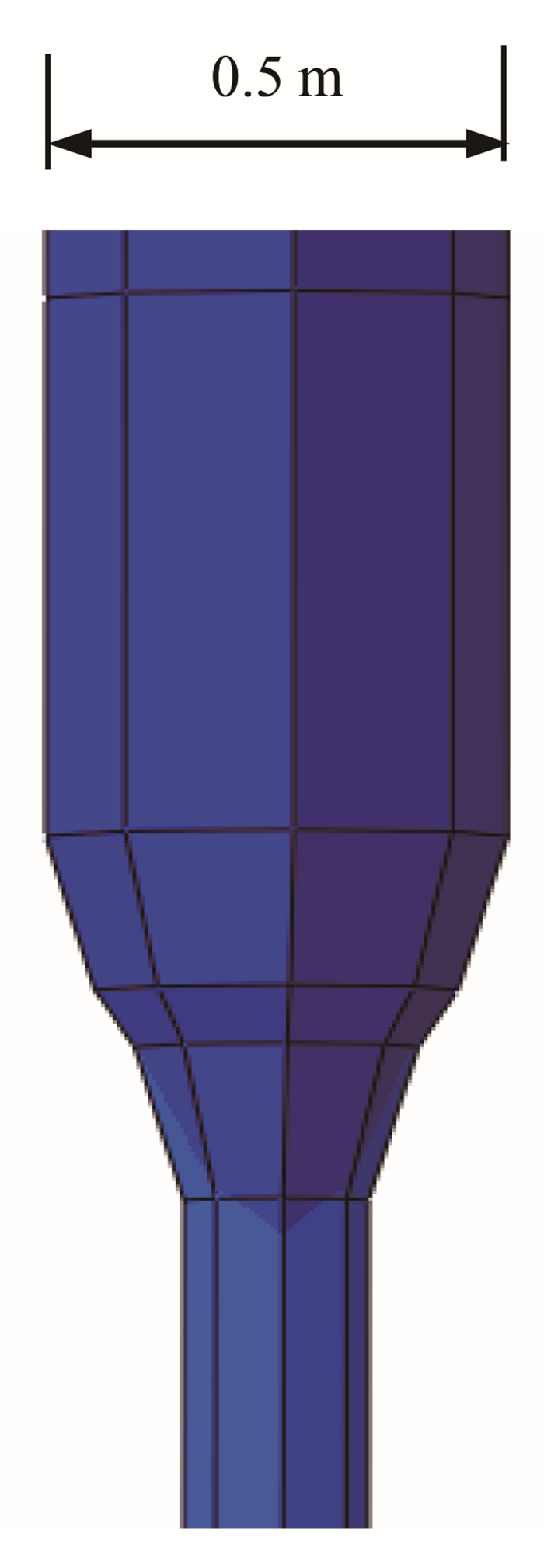
由于既有桩的存在,实际邻近既有桩的新桩贯入三维问题并非中心对称问题,不能简化为二维模型。因此,本节建立了邻近既有桩的静压沉桩三维数值模型,如图 4所示。模型中土体高度为30 m,半径为10 m;新桩桩径为0.5 m,桩长为20 m,沉桩位置位于土体中心;既有桩桩长20 m,桩径为0.5 m,桩中心距离新桩沉桩位置中心2 m,为4倍桩径。由于新桩贯入导致土体开裂不属于连续介质问题,且与土体的抗拉强度有关系,因此为了保证沉桩过程中不发生土体单元的畸变,保证模型的收敛性,本文模型在新桩沉桩位置预设半径为0.1 m的小孔,在桩端底部加上半径为0.1 m的辅助管,在桩和桩靴、桩靴和下端的辅助管之间采用光滑过渡(图 5)。同时利用排开土体体积相等的原则,计算具有辅助管的新桩模型等效半径,即
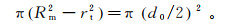 (11)
(11)
|
| 图 4 邻近既有桩沉桩有限元模型 Fig. 4 Finite element model of pile penetration adjacent to existing pile |
|
|
|
| 图 5 新桩桩端样式 Fig. 5 New pile tip |
|
|
式中:Rm为模型桩半径;rt为辅助管半径。可得
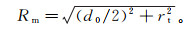 (12)
(12) 桩体及桩端下部小管用线弹性本构模型来模拟,在材料模块选用线弹性本构模型并给出弹性模量和泊松比2个参数。由于建立数值模型的目的是验证本文理论解答的合理性,因此为与理论解答保持一致,土体本构模型也采用弹性模型来模拟并给出弹性模量和泊松比2个参数。土体材料参数和桩身材料参数如表 1所示。土体和桩身均采用八节点六面体单元,土体、新桩和既有桩的单元数分别为26 240、324和160。
| 弹性模量/MPa | 泊松比 | |
| 土体 | 6 | 0.3 |
| 既有桩桩身 | 20 000 | 0.2 |
| 新桩桩身 | 20 000 | 0.2 |
| 桩端辅助管 | 20 000 | 0.2 |
所建立的有限元模型包含2个分析步,分别为地应力平衡和新桩贯入。地应力平衡通过Geostatic分析步来实现,其中土体重力通过体力来施加。新桩贯入过程的模拟通过位移控制法来实现,即在桩顶施加竖直向下的位移使桩身下沉。在这一分析步中,约束土体底部边界的竖向和水平位移,以及土体侧面边界的水平位移,同时控制桩身的水平位移。本文通过设置分析步时间和桩身竖向位移的幅值来控制沉桩速度。
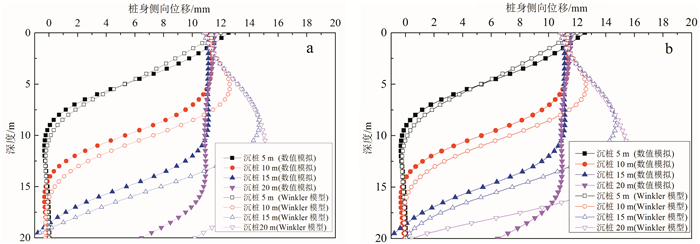
3.2 结果分析图 6为本文理论方法采用Winkler地基模型的计算结果和数值模拟结果对比图。可以看出,理论模型和数值模拟均显示既有桩桩身变形随新桩贯入深度的增加逐渐变大。从变形规律上看,理论模型和数值模拟计算结果保持了较好的一致性。从变形的量值来看:在新桩贯入10 m深度以内,理论计算结果和数值模拟结果基本一致;当静压桩沉入深度≥10 m时,理论计算结果略大于数值模拟结果。这主要是由于数值模型采用了在沉桩位置预设辅助孔的原因;同时,对于理论方法,沉桩运用半无限土体中的球孔扩张来模拟,该方法主要体现的是沉桩过程中桩身对周围土体的挤压作用,而关于桩身对周围土体的剪切作用则不能很好地模拟,这就导致理论计算的侧向挤土位移大于数值模拟计算结果。
|
| a. 桩端自由;b. 桩端固定。 图 6 数值模拟和Winkler地基模型计算结果对比 Fig. 6 Comparison between numerical simulation and analytical model |
|
|
对比图 6a、b可以发现:不同的桩端约束形式对新桩沉桩5、10、15 m时既有桩桩身侧向位移基本没有影响;但当新桩贯入接近20 m时,桩端固定的既有桩桩身下部侧向位移明显小于桩端自由的既有桩桩身下部侧向位移。这主要是由于当新桩沉桩长度较小时,其对既有桩的影响仅为桩身上部,桩端的约束形式影响很小;而当新桩贯入深度接近或者达到既有桩入土深度时,桩端的约束形式限制了下部桩身的位移,因此对桩身下部的变形影响明显。
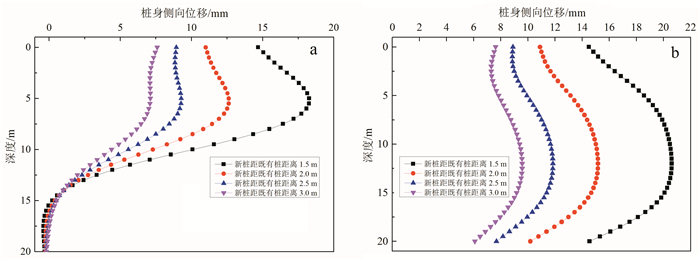
4 影响因素 4.1 新桩和既有桩距离为讨论新桩沉桩和邻近既有桩距离对既有桩桩身位移的影响,用本文理论方法分别计算了新桩和既有桩距离为1.5、2.0、2.5、3.0 m情况下新桩贯入10、20 m时的既有桩桩身侧向位移,如图 7所示。
|
| a. 新桩沉桩10 m;b. 新桩沉桩20 m。 图 7 新桩沉桩和既有桩距离对既有桩桩身侧向位移的影响 Fig. 7 Influence of the distance between new pile and existing pile on deformation of existing pile |
|
|
可以看出,随着新桩距既有桩距离的减小,既有桩桩身侧向位移显著增加,且在新桩距既有桩距离较小时,相同幅度距离的减小引起的既有桩桩身侧向位移值大幅增加。沉桩10 m时:当距离从2.0 m减小至1.5 m时,既有桩桩身侧向位移最大值从12.62 mm增加至18.27 mm,增加量为5.65 mm;而距离从3.0 m减小至2.5 m时,侧向位移最大值从7.11增加至9.27 mm,增加量仅为2.16 mm。沉桩20 m时:当距离从2.0 m减小至1.5 m时,既有桩桩身侧向位移最大值从15.17 mm增加至20.61 mm,增加量为5.44 mm;而距离从3.0 m减小至2.5 m时,侧向位移最大值从9.78 mm增加至11.84 mm,增加量仅为2.06 mm。这表明增大与既有桩之间的距离对减小挤土作用的效果明显。
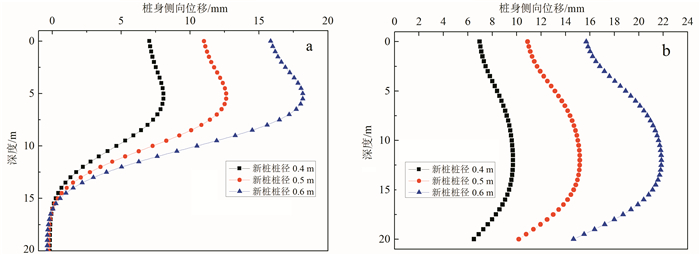
4.2 新桩桩径为研究新桩桩径对沉桩引起邻近既有桩内力和变形的影响,选取新桩直径为0.4、0.5、0.6 m 3种情况分别进行计算,图 8为新桩沉桩10和20 m时既有桩的桩身侧向位移。
|
| a. 新桩沉桩10 m;b. 新桩沉桩20 m。 图 8 新桩桩径对既有桩桩身侧向位移的影响 Fig. 8 Influence of new pile diameter on deformation of existing pile |
|
|
从图 8中可以看出,随着桩径的增大,挤土效应引起的既有桩桩身侧向位移更加明显。沉桩10 m时:当桩径从0.4 m增大至0.5 m时,既有桩桩身侧向位移最大值从8.08 mm增加至12.62 mm,增加量为4.54 mm;桩径从0.5 m增加至0.6 m时,桩身侧向位移最大值从12.62 mm增加至18.17 mm,增加量为5.55 mm。沉桩20 m时:当桩径从0.4 m增大至0.5 m时,既有桩侧移最大值从9.71 mm增加至15.17 mm,增加量为5.46 mm;桩径从0.5 m增加至0.6 m时,桩身侧向位移最大值从15.17 mm增加至21.85 mm,增加量为6.68 mm。这表明,减小桩径对降低新桩贯入对既有桩影响的效果比增大沉桩距离对减小挤土效应的效果更加明显。因此,在新桩布桩时尽量远离既有桩,且新桩尽量通过增加桩长而非增大桩径来满足承载力要求,也即尽量选择细长桩。
5 结论1) 本文理论分析方法与数值模拟取得结果基本一致,验证了本文理论解答的准确性。
2) 桩端约束形式仅影响桩端附近桩身变形,当新桩沉桩深度小于既有桩桩长时,桩端约束形式影响很小,可按桩端自由考虑;当新桩贯入接近或者超过既有桩桩端时,桩端约束形式影响较大,需要慎重考虑。
3) 新桩距既有桩距离和新桩桩径对既有桩变形影响较大,随着桩径的增加,既有桩变形均逐渐增大;随着新旧桩之间距离的增加,既有桩变形显著减小。新桩布桩时尽量远离既有桩,且尽量选择细长桩。
| [1] |
贾水钟, 贾晓峰. 浅析静安顺德苑工程的老桩利用问题[J]. 建筑结构, 2007, 37(增刊1): 477-480. Jia Shuizhong, Jia Xiaofeng. Settlement Design of Making Use of the Old Bored Pile in Jing'an Shunde Building[J]. Building Structure, 2007, 37(Sup.1): 477-480. |
| [2] |
姚建平. 既有桩再利用及新旧桩混合使用条件下的静压新桩施工控制工艺研究[J]. 建筑施工, 2016, 38(4): 402-405. Yao Jianping. Study on Construction Control Technology for New Static Pressure Piles Under Condition of Recycled Existing Piles and New-Old Mixed Piles[J]. Building Construction, 2016, 38(4): 402-405. |
| [3] |
王龙胜, 衣倩倩, 张斌. 既有桩基耐久性评估及再利用分析研究[J]. 工程建设, 2017, 49(5): 25-28. Wang Longsheng, Yi Qianqian, Zhang Bin. Analytical Study on Reuse of Existing Pile Foundation and Its Durability Evaluation[J]. Engineering Construction, 2017, 49(5): 25-28. |
| [4] |
Leung C F, Chow Y K, Shen R F. Behavior of Pile Subject to Excavation Induced Soil Movement[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2000, 126(11): 947-954. DOI:10.1061/(ASCE)1090-0241(2000)126:11(947) |
| [5] |
Leung C F, Lim J K, Shen R F, et al. Behavior of Pile Groups Subject to Excavation-Induced Soil Movement[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2003, 129(1): 58-65. DOI:10.1061/(ASCE)1090-0241(2003)129:1(58) |
| [6] |
Leung C F, Ong D E L, Chow Y K. Pile Behavior due to Excavation-Induced Soil Movement in Clay: II: Collapsed Wall[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2006, 132(1): 45-53. DOI:10.1061/(ASCE)1090-0241(2006)132:1(45) |
| [7] |
Poulos H G, Chen L T, Hull T S. Model Tests on Single Piles Subjected to Lateral Soil Movement[J]. Soil and Foundations, 1995, 35(4): 85-92. DOI:10.3208/sandf.35.4_85 |
| [8] |
Chen L T, Poulos H G, Hull T S. Model Tests on Pile Groups Subjected to Lateral Soil Movement[J]. Soil and Foundations, 1997, 37(1): 1-12. DOI:10.3208/sandf.37.1 |
| [9] |
Sagaseta C. Analysis of Undrained Soil Deformation due to Ground Loss[J]. Géotechnique, 1987, 37(3): 67-86. |
| [10] |
Sagaseta C, Whittle A J. Prediction of Ground Movements due to Pile Driving in Clay[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2001, 127(1): 55-66. DOI:10.1061/(ASCE)1090-0241(2001)127:1(55) |
| [11] |
周火垚, 施建勇. 饱和软黏土中足尺静压桩挤土效应试验研究[J]. 岩土力学, 2009, 30(11): 3291-3296. Zhou Huoyao, Shi Jianyong. Test Research on Soil Compacting Effect of Full Scale Jacked-in Pile in Saturated Soft Clay[J]. Rock and Soil Mechanics, 2009, 30(11): 3291-3296. DOI:10.3969/j.issn.1000-7598.2009.11.012 |
| [12] |
张明义, 刘雪颖, 王永洪, 等. 粉土及粉质黏土对静压沉桩桩端阻力影响机制现场试验[J]. 吉林大学学报(地球科学版), 2020, 50(6): 1804-1813. Zhang Mingyi, Liu Xueying, Wang Yonghong, et al. Feild Test on Influencing Mechanism of Silty Soil and Silty Clay on Tip Resistance of Static Pressure Pile[J]. Journal of Jilin University (Earth Science Edition), 2020, 50(6): 1804-1813. |
| [13] |
罗战友, 夏建中, 龚晓南, 等. 考虑孔压消散的静压单桩挤土位移场研究[J]. 岩石力学与工程学报, 2014, 33(增刊1): 2765-2772. Luo Zhanyou, Xia Jianzhong, Gong Xiaonan, et al. Study of Compacting Soil Displacements Around Jacked Single Pile Based on Excess Pore Pressure Dissipation[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(Sup. 1): 2765-2772. |
| [14] |
张亚国, 李镜培. 软黏土中静压沉桩引起的侧向挤土位移分析[J]. 同济大学学报(自然科学版), 2015, 43(12): 1801-1806. Zhang Yaguo, Li Jingpei. Lateral Displacements of Ground Caused by Piles Installation in Soft Clay[J]. Journal of Tongji University (Natural Science), 2015, 43(12): 1801-1806. DOI:10.11908/j.issn.0253-374x.2015.12.006 |
| [15] |
朱宁, 施建勇, 陈海丰. 一种半无限土体中圆孔扩张的分析方法[J]. 岩土力学, 2006, 27(2): 257-260. Zhu Ning, Shi Jianyong, Chen Haifeng. A Method for Cavity Expansion in Semi-Infinite Soil[J]. Rock and Soil Mechanics, 2006, 27(2): 257-260. DOI:10.3969/j.issn.1000-7598.2006.02.016 |
| [16] |
Vesic A S. Bending of Beams Resting on Isotropic Elastic Solids[J]. Journal of Soil Mechanics and Foundation Engineering, ASCE, 1961, 87(2): 35-53. |


