2. 东南大学岩土工程研究所, 南京 210009
2. Institute of Geotechnical Engineering, Southeast University, Nanjing 210009, China
0 引言
进行岩土工程风险评价时,往往假定设计参数为正态分布或对数正态分布,如采用随机场模拟岩土体参数空间变异性[1]、设计参数与原位测试参数之间的进行模型转换[2-3]、贝叶斯分析[4]、极大似然估计[5]和桩基可靠性设计[6]等。岩土参数的正态分布特性可采用统计检验法进行判定,目前最常用的为Shapiro-Wilk(SW)检验、Kolmogorov-Smirnov(KS)检验、Lilliefors(LF)检验和Anderson-Darling(AD)检验[7-8]等。
目前,岩土工程中广泛采用KS检验进行正态性检验:陈立宏等[9]采用KS检验,对水利工程中抗剪强度试验数据进行正态分布特性分析,验证了正态分布和对数正态分布的适用性;严春风等[10]提出了基于Bayes理论的正态检验方法,将经典的检验法与Bayes理论相结合;张继周等[11]探讨了岩土参数概率分布类型,并采用KS检验对南京淤泥质粉质粉土强度和变形参数的正态分布特性进行了验证;Phoon等[3]将KS检验应用于多变量的正态性检验中,构建了多变量正态分布的边缘概率密度。
然而,Razali等[7]研究指出,相较于其他检验方法,在小样本(n < 2 000)条件下KS检验功效最低。章刚勇等[12]的研究同样证实了该结论,他同时指出若样本容量n < 200,则各正态性检验方法之间可能并不存在显著的差异。在岩土工程中,用于测试数据的样本容量通常限制在较小的范围内,理论上KS检验并不一定能给出最佳正态分布检验的判定结果。不同正态性检验方法对岩土工程参数资料的检验结果和效果有无异同尚未得到证实,关于工程实践中应该选择何种检验方法的研究也未得到开展。
受到项目成本和时间限制,常规岩土工程勘察难以获得大量具有代表性的测试数据,使得岩土参数的正态分布检验受到样本容量的限制。孔压静力触探(CPTU)高精度原位测试技术[13],测试数据具有扰动小、容量大、重复性好等特点,非常适合岩土参数统计分析。
本文以宿迁废黄河泛滥沉积相粉土中的孔压静力触探锥尖阻力(qt)测试资料为研究对象,采用SW检验、KS检验、LF检验和AD检验等4种方法对该测试数据进行了正态性检验研究,分析上述不同正态性检验方法的异同点和检验效果,以降低设计参数的不确定性。
1 正态性检验方法由于以往研究普遍认为qt服从对数正态分布[4, 14],为保持一致性,本文对ln(qt) 进行正态性检验,即当qt服从对数正态分布时,ln(qt) 应当服从正态分布。正态性检验方法一般采用如下假设形式[7]:
H0表示数据服从正态分布;
H1表示数据不服从正态分布。
根据所应用统计学特性(如偏度系数、峰度系数、分布曲线和相关系数)的不同,衍生出不同的正态性检验方法,分别简要介绍如下。
1.1 SW检验SW检验是基于偏度和峰度引起数据非正态性的检验方法[7],并由于其具有良好的功效而得到广泛认可。对于给定的随机样本,排序后记为x1 < x2 < … < xn,则SW检验量W定义[7]为
 (1)
(1) 式中:n为样本容量;xi为第i阶统计量;x为样本均值;ai为权重系数,可查分位表得出。W统计量可以视为,基于顺序统计量某种线性组合的平方得出的方差最优估计量与数据样本方差之间的比值。
根据给定的显著水平α和样本容量n,查统计量W的p分位数表,确定α分位数临界值Wα。若W < Wα,则拒绝H0,认为数据不服从正态分布;反之,则不拒绝H0。W统计量分布具有较大的偏度,接近于1的W值也可能导致拒绝正态性原假设。由于不同方法涉及的临界值有所差异,统计学中倾向于表述为概率值(P)形式,以获得更为一般化的判定结果。若P = P(W≥ Wα) >α,则不拒绝H0。本文中显著水平α取值为0.05,与常用的统计分析相符合。
1.2 KS检验KS检验属于经验分布函数检验法,其检验量定义为理论分布曲线与经验分布曲线之间的最大竖向差值[7]。给定n个排序后的数据点x1 < x2 < … < xn,KS检验统计量T定义[7]为
 (3)
(3) 式中:F*(x)为理论累积分布曲线函数;Fn(x)为经验累积分布曲线函数,从样本中估计得出。若检验统计量T超过了对应显著水平α下的临界值T1-α,则拒绝H0。以概率表述为,若P值大于显著水平α,则不拒绝H0。
KS可以检验样本数据是否服从正态分布,也可以检验数据是否服从其他分布[7, 12]。对于正态分布检验,需要给定理论分布曲线的均值和标准差,然而这两个统计量是未知的。因此,采用KS检验时,对任意分布未知的随机样本,需先将样本数据标准化,然后用于KS检验中。
1.3 LF检验LF检验是对KS检验的修正,从样本数据中估计理论分布曲线的参数,以解决KS检验中参数未知的问题。类似地,LF检验统计量D定义[7]为
 (4)
(4) 式中,Sn(x)为样本累积分布曲线函数。若D超出对应显著水平下的临界值,则拒绝H0。以概率表述为,若P值大于显著水平α,则不拒绝H0。LF检验统计量的临界值可查分位表得出。
尽管LF检验统计量的定义与KS检验类似,然而两者的临界值完全不同,从而可能推导出完全不同的正态性判断结论[12]。
1.4 AD检验AD检验也属于经验分布函数检验法,其利用经验累积分布曲线函数和理论累积分布曲线函数之差的平方和来构建检验统计量。AD检验统计量A2的定义[7, 12]如下:
 (5)
(5) 式中,φ(F*(x))为非负权重函数,φ(F*(x))={[F*(x)[1-F*(x)]}-1。D’Agostino和Stephens提出修正的AD检验统计量An2,对A2进行样本容量的修正[7]:
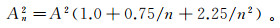 (6)
(6) 同样,对于给定显著水平α,若检验统计量An2大于临界值An,1-α2,则拒绝H0。同样以概率表述为,若P值大于显著水平α,则不拒绝H0。
1.5 正态检验方法的分析统计学中正态性检验方法通常采用功效进行评价,由于数值模拟的随机性,可能会产生如下两类错误[7, 12]:当原假设为真时,可能做出拒绝的决策,称为第Ⅰ类错误(拒真);当原假设为错误时,可能做出接纳的决策,称为第Ⅱ类错误(纳假)。当样本容量确定时,犯两类错误的概率不同时被控制,通常是在控制犯第Ⅰ类错误的概率(表述为显著水平α)条件下,使得犯第Ⅱ类错误的概率β较小[7, 12]。此时,功效定义为拒假的概率,即(1-β)。因此,功效越大,则表明该正态性检验方法越能够对非正态分布的数据产生拒绝H0的判定,相应准确性越高。
根据以往的研究[7, 12],在样本容量低于2 000时,SW检验结果最佳的正态性检验结果,其次为AD检验和LF检验,而KS检验的功效最低。从岩土工程实际来看,岩土参数的正态性通常是未知的,需要应用检验方法进行判定,本文采用工程案例进行了研究,对上述推断进行验证。
2 工程试验资料 2.1 试验概况多功能CPTU试验采用美国原装进口多功能数字式车载CPTU系统,配备了最新的多功能测试探头。探头规格符合国际标准:锥角60°,锥底直径35.7 mm,锥底截面积为10 cm2,侧壁摩擦筒表面积150 cm2,孔压测试元件厚度5 mm,位于锥肩位置,测得孔隙水压力为u2。贯入速率为2 cm/s,沿深度每5 cm测试一组读数。贯入设备采用重型卡车,利用螺旋地锚提供反力,具有自动调平装置能够满足大多数的地形条件。贯入过程中连续测读锥尖阻力qt、侧壁摩擦力fs及u2。
试验场地位于江苏省宿(迁)新(沂)高速公路宿迁段K460+500 m处施工段,地质构造主要为北东向构造,处于活动状态的郯庐断裂带,为地震活动带。试验场地地貌类型以废黄河堆积冲积平原、堆积波状平原为主,零星分布剥蚀残丘。该地段全为第四系松散沉积物。场区表层为近期人工杂填土及耕植土,其下均为粉土和粉砂,地下水位3.8 m。试验场地土层的主要物理力学指标如表 1所示。共计17个CPTU测试孔,典型测试剖面如图 1所示。
| 层号 | 土名 | 层厚/m | 比重 | w(黏粒)/% | 含水量/% | 液限/% | 塑性指数 | 标贯锤击数 |
| ① | 素填土 | 1.5 | 2.71 | 14.9 | 22.4 | 26.2 | 8.8 | 9 |
| ② | 粉土 | 3.8 | 2.70 | 3.7 | 24.1 | 28.1 | 5.8 | 4 |
| ③ | 粉质砂土 | 9.4 | 2.69 | 5.4 | 33.6 | 28.7 | 5.7 | 10 |
| ④ | 粉土夹粉砂 | 未揭穿 | 2.68 | 5.6 | 23.6 | 31.6 | 11.3 | 24 |

|
| 图 1 典型CPTU测试结果 Fig. 1 Typical results of CPTU tests |
|
|
Phoon等[15]研究指出,当不同的地质单元混杂时,分析结果将会高估土体的变异性,即土体的变异系数(定义为标准差与均值之比)高于真实值。Fenton[14]研究表明,若两种不同地质单元的数据混合在一起,则测试数据的直方图表现出双峰特征,数据的正态性也会降低。Amundaray[16]和Rethati[17]分别研究了样本容量对岩土参数变异系数统计的影响,指出样本容量不低于30,即可得到稳定可靠的变异系数。因此,为得到有意义的均值和标准差结果,应当将不同地质单元的土体分别进行统计分析,同时保证样本容量足够大。
本研究中选定第③层(粉质砂土)作为研究对象,获得了17个土层剖面。从抽样的角度上讲,整个土层空间内的锥尖阻力可视为总体,而单次CPTU测试数据则为总体的一次抽样结果。通常,抽样不可能获得总体的所有信息,只能从有限的测试资料中获得推断。因此统计分析中样本容量应当足够大,才能获得足够的代表性,为此需要将多个CPTU剖面综合在一起进行分析,以获得更一致的判定结果。
当样本来自于相同总体时,其均值为对总体的无偏估计,此时各样本之间的均值应当相等。因此,在进行正态性检验之前,应当首先进行均值检验。从土力学角度上讲,该检验的目的在于保证各CPTU测试信息均来源于同一土层,以确保获得具有统计意义的分析结果。在通过均值检验之后,则可对所有数据进行正态性检验。
3 试验结果分析 3.1 基于ANOVA的均值检验ANOVA检验是统计学中对各组数据进行均值检验的一种常用方法,其假设[18-19]为:
H0表示各组数据均值相等,即μ1=μ2=…=μn;
H1表示至少有两组数据的均值不相等。
数据均值之间的区别来自于以下两种不同的变异性[18-19]:1)各组数据内部的空间变异性,也称为组内变异性(SE);2)各组数据之间的空间变异性,也称为组间变异性(ST)。若组间变异性显著大于组内变异性,则表明样本之间存在显著的差异。总变异性(Ssum)为组间变异性和组内变异性之和。数学表达式[18-19]分别为:
 (7)
(7) 式中:a为样本的个数;yij为第i个样本的第j个观测值;y为所有样本构成集合的均值;yi为第i个样本的均值。ANOVA检验要求各样本容量相等。
根据式(7)得到的组间和组内的方差分别与各自的自由度有关,无法直接比较,因此,需要利用自由度对方差进行标准化处理,从而构建检验统计量F[18-19]为
 (8)
(8) 式中:SMT为组间标准差,SMT=ST/νT;SME为组内标准差,SME=SE/νE;νT和νE分别为组间和组内样本的自由度,νT=a-1,νE = a(n - 1)。若F趋近于1,则表明组间变异性接近于组内变异性,样本之间的变异性并不明显,无充分的理由拒绝H0。给定显著水平α = 0.05,查F检验统计表,可得相应的临界值F0,若F > F0,则拒绝H0。同样更一般地表述为概率形式,若P值小于α,则拒绝H0。
首先对17个土层剖面的qt数据进行ANOVA检验,逐步排除其中使得组间方差较大的剖面,若最终剩余的样本能够通过ANOVA检验,此时认为样本能够代表同一土层的测试信息。根据检验结果,所识别出的土层单元共计12个,单个测试孔样本容量为155,所有样本的总体容量为1 860。表 2给出了各样本的基本统计量信息。
| 孔号 | 样本容量 | 最大值/ MPa | 最小值/ MPa | 均值/ MPa | 标准差 | 变异系数/% |
| 1 | 155 | 13.32 | 2.71 | 7.43 | 2.21 | 29.69 |
| 2 | 155 | 12.03 | 2.13 | 7.19 | 2.14 | 29.81 |
| 3 | 155 | 12.20 | 2.35 | 7.04 | 2.11 | 30.00 |
| 4 | 155 | 11.97 | 2.25 | 7.41 | 1.98 | 26.67 |
| 5 | 155 | 12.30 | 2.05 | 6.94 | 2.09 | 30.15 |
| 6 | 155 | 12.60 | 2.48 | 7.40 | 2.39 | 32.30 |
| 7 | 155 | 12.45 | 2.99 | 7.70 | 2.12 | 27.55 |
| 8 | 155 | 13.32 | 2.09 | 6.87 | 2.36 | 34.37 |
| 9 | 155 | 12.49 | 2.35 | 7.39 | 2.14 | 28.95 |
| 10 | 155 | 12.05 | 2.79 | 7.33 | 1.92 | 26.17 |
| 11 | 155 | 11.95 | 2.13 | 7.41 | 2.14 | 28.89 |
| 12 | 155 | 11.82 | 2.02 | 7.37 | 2.26 | 30.64 |
表 3为ANOVA检验的统计分析表,对于所选择的12个剖面,其检验统计量F值趋近于1,表明组间变异性并不显著,而P=0.07>α=0.05,因此不拒绝H0。图 2为根据基本统计量信息得到的箱形图,其中本体是指剔除了奇异值和极值之后的剩余数据。从图 2可以看出,各样本本体的中位数均在7.30附近小幅度波动,最大值、最小值、上四分位数和下四分位数也在相应的均值附近小幅度变化,同样表明样本有很大可能来自于同一总体。因此,上述12组样本用于后续的正态性检验中。
| 变异性来源 | 方差 | 自由度 | 均方差 | F | P |
| 组间 | 66.5 | 11 | 6.05 | 1.30 | 0.07 |
| 组内 | 8 612.8 | 1 848 | 4.66 | ||
| 总变异性 | 8 679.3 | 1 850 |

|
| 图 2 均值检验箱形图 Fig. 2 Box plot for checking constant mean value |
|
|
对所有12个样本数据进行正态性检验,来判断第③层(粉质砂土)ln(qt/MPa)的概率密度分布规律,样本容量n=1860。为保持正态性检验的一致性,将样本数据进行标准化处理,如公式(9)所示:
 (9)
(9) 式中:xi为集合中第i个测量值(即ln(qt/MPa)i)标准化后的第i个元素;μ和σ分别为集合的平均值和标准差。当原集合{ln(qt/MPa)}服从正态分布时,{xi}应当服从标准正态分布,因此上述标准化过程并不影响结论的一致性。
图 3给出了不同检验方法的检验统计量P值、直方图、拟合的标准正态分布曲线以及偏度系数和峰度系数。从图 3可以看出,归一化处理后ln(qt/MPa)的直方图均值趋近于0,基本上具有对称性,因此偏度系数非常小;直方图的峰值略微高于拟合曲线,差值并不显著,因此峰度系数也较低。根据上述分析,可以认为数据倾向于服从正态分布。然而值得指出的是,这一集合并不一定能够充分代表土层的信息,仍然仅仅是对总体的估计。

|
| 图 3 样本的正态分布检验 Fig. 3 Normality test on the selected samples |
|
|
采用4种正态分布检验方法对集合的正态性进行判定,SW检验、LF检验和AD检验的P值均低于(或≤)0.005,均远远低于显著水平α=0.05,因此根据这3种检验方法,数据并不具有正态性。然而KS检验的P值为0.087,显著水平最高,因此根据KS检验结果,不能拒绝正态性假定。从直方图上看,样本数据大体上服从正态性分布。
为检验不同样本容量时4种检验方法的特征,对集合进行随机抽样,样本容量分别设为50, 100, 150, …, 1 800,对每个给定的样本容量分别独立抽样500次,统计相应的P值和不拒绝正态性(H0)假定的频率(定义为500次抽样检验中不拒绝H0的次数与抽样次数的比值)。这一频率反映了不同检验方法在不同样本容量条件下不拒绝正态性检验的概率大小。
考虑到岩土工程参数通常具有显著的自相关结构,且表现出随深度变化的趋势[20-23],在本研究中进行正态性检验时,对样本数据重新进行了排序,未涉及相关性分析和坐标的运算;因此,基于样本数据的随机抽样结果仍然是具有物理意义的。图 4给出了样本容量为200时某次抽样结果与实际测量剖面的对比,所有数据均从小至大进行了排列,可以看出从数值大小上抽样结果能够与实际测量剖面形成较好的对比。

|
| 图 4 排序后随机样本与实测数据对比 Fig. 4 Comparison of ordered random sample and measured data |
|
|
图 5给出了不同样本容量下不拒绝H0的频率,可以看出随着样本容量的增加,对4种检验方法而言,不拒绝H0的频率逐渐减小。这种现象可以解释为,随着样本容量的增加,检验的功效增大,检验更为严格、可靠,因此有越大的概率拒绝正态性假定。同时可以看出:在样本容量n < 2000的条件下,KS检验给出了最高不拒绝H0的频率,即便样本容量达到1 800时,500次抽样中也有40%的样本能够通过KS检验;SW检验则最为严格,当样本容量达到400时,500次抽样检验中拒绝H0的频率已经超过50%;而LF检验和AD检验介于两者之间,但同样当样本容量超过400时,不拒绝H0的频率快速降低。再次证明在小样本容量条件下,KS检验给出最不保守的正态性判定结果,而SW检验最为严格。

|
| 图 5 排序后随机样本与实测数据对比 Fig. 5 Comparison of ordered random sample and measured data |
|
|
此外,从图 5中也可以看出,当样本容量n < 200时:各检验方法给出的不拒绝H0的频率均高于70%,在SW、LF和AD检验之间几乎不存在显著的区别;而KS检验的不拒绝H0的频率稳定在95%附近,始终给出最不保守的检验结果。
3.3 检验结果讨论在实际岩土工程中,岩土参数的正态性是未知的,判定结果取决于参数的不确定性程度、检验方法、样本容量和变异性强弱等多重因素影响。根据前述分析结果,通常当样本容量充足(n>200)时,SW检验结果最为严格,KS检验结果最不保守,不拒绝H0的概率最高,LF检验和AD检验结果则介于两者之间;当样本容量较小时(n < 200),SW检验、LF检验和AD检验结果无显著区别,KS检验结果最不保守,与前述3种检验方法差异较大。
若样本无法满足正态性假定,则建议采用正态转换方法将非正态分布的样本转换为正态分布,然后用于后续设计中,常用的正态转换方法有Box-Cox转换和Johnson分布族转换[3]等。
然而在岩土工程可靠度分析中,并不需要采用严格的正态性假定,如Phoon等[3]利用非正态分布的随机变量构建了基于多变量正态分布的设计参数转换模型,并指出该模型能够提供具有实践意义的设计参数估计结果。从岩土工程风险分析角度讲,采用严格或宽松的正态性假定应当取决于工程风险等级。在岩土工程可靠性分析中,测试数据应保证拥有足够的样本容量,在常规岩土工程设计中,设计参数不确定性较低,采用KS检验结果即可满足稳定性分析要求;在复杂岩土工程设计中,设计参数不确定性较高,需采用SW检验对设计参数进行正态性检验,以降低设计方案风险。
4 结论1) 岩土参数的正态性检验需要大量代表性的数据资料,当多个样本综合进行检验时,建议首先采用ANOVA检验,从总体测试数据中筛选具有代表性的样本。
2) 当样本容量充足时,SW检验结果最为严格,KS检验结果最不保守,LF检验和AD检验结果介于两者之间;当样本容量较小时,SW检验、LF检验和AD检验结果相似,KS检验结果与前述3种检验方法差异较大。
3) 当测试数据的样本容量充足时,在常规岩土工程设计中,采用KS检验结果即可满足稳定性分析要求;在复杂岩土工程设计中,需采用SW检验对设计参数进行正态性检验,以降低设计方案风险。
| [1] |
Phoon K K. Modeling and Simulation of Stochastic Data[C]//Proceedings of GeoCongress. Reston: ASCE, 2006: 1-17.
|
| [2] |
Phoon K K, Ching J Y. Beyond Coefficient of Variation for Statistical Characterization of Geotechnical Parameters[C]//Proceedings of the 4th International Conference on Site Characterization 4. [S.l.]: Staff Publications, 2012: 113-130.
|
| [3] |
Phoon K K, Ching J Y. Multivariate Model for Soil Parameters Based on Johnson Distributions[C]//Foundation Engineering in the Face of Uncertainty. [S.l.]: Geotechnical Special Publication, 2013: 337-353.
|
| [4] |
Cao Z J, Wang Y. Bayesian Approach for Probabilistic Site Characterization Using Cone Penetration Tests[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2013, 139(2): 267-276. DOI:10.1061/(ASCE)GT.1943-5606.0000765 |
| [5] |
Degroot D J, Baecher G B. Estimating Autocovariance of In-Situ Soil Properties[J]. Journal of Geotechnical Engineering, 1993, 119(1): 147-166. DOI:10.1061/(ASCE)0733-9410(1993)119:1(147) |
| [6] |
Phoon K K, Kulhway F H, Grigoriu M D. Multiple Resistance Factor Design for Shallow Transmission Line Structure Foundation[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2003, 129(9): 807-818. DOI:10.1061/(ASCE)1090-0241(2003)129:9(807) |
| [7] |
Razali N M, Wah Y B. Power Comparisons of Shapiro-Wilk, Kolmogorov-Smirnov, Lilliefors and Anderson-Darling Tests[J]. Journal of Statistical Modeling and Analytics, 2011, 2(1): 21-33. |
| [8] |
Park H M. Univariate Analysis and Normality Test Using SAS, STATA, and SPSS[R]. Bloomington: Indiana University, 2008.
|
| [9] |
陈立宏, 陈祖煜, 刘金梅. 土体抗剪强度指标的概率分布类型研究[J]. 岩土力学, 2005, 26(1): 37-45. Chen Lihong, Chen Zuyu, Liu Jinmei. Probability Distribution of Soil Strength[J]. Rock and Soil Mechanics, 2005, 26(1): 37-45. DOI:10.3969/j.issn.1000-7598.2005.01.008 |
| [10] |
严春风, 陈洪凯, 张建辉. 岩石力学参数的概率分布的Bayes推断[J]. 重庆建筑大学学报, 1997, 19(2): 65-71. Yan Chunfeng, Chen Hongkai, Zhang Jianhui. The Use of Bayesian Method to Infer Distribution of Mechanical Parameters[J]. Journal of Chongqing Jianzhu University, 1997, 19(2): 65-71. |
| [11] |
张继周, 缪林昌. 岩土参数概率分布类型及其选择标准[J]. 岩石力学与工程学报, 2009, 28(增刊2): 3526-3532. Zhang Jizhou, Miao Linchang. Types and Selection Criteria of Probability Distribution of Rock and Soil Parameters[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(Sup.2): 3526-3532. |
| [12] |
章刚勇, 阮陆宁. 基于Monte Carlo随机模拟的几种正态性检验方法的比较[J]. 统计与决策, 2011(7): 17-20. Zhang Gangyong, Ruan Luning. A Comparison on Several Tests for Normality by Monte Carlo Simulation[J]. Statistics and Decision, 2011(7): 17-20. |
| [13] |
Cai G J, Liu S Y, Puppala A J. Comparison of Cpt Charts for Soil Classification Using PCPT Data: Example from Clay Deposits in Jiangsu Province, China[J]. Engineering Geology, 2011, 121: 89-96. DOI:10.1016/j.enggeo.2011.04.016 |
| [14] |
Fenton G. Random Field Modeling of CPT Data[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1999, 125(6): 486-498. DOI:10.1061/(ASCE)1090-0241(1999)125:6(486) |
| [15] |
Phoon K K, Kulhawy F H. Characterization of Geotechnical Variability[J]. Canadian Geotechnical Journal, 1999, 36(4): 612-624. DOI:10.1139/t99-038 |
| [16] |
Amundaray J I. Modeling Geotechnical Uncertainty by Bootstrap Resampling[D]. West Lafayette: Purdue University, 1994.
|
| [17] |
Rethati L. Probabilistic Solutions in Geotechnics[M]. Budapest: Elsevier, 1988.
|
| [18] |
Cornell J R, Benjamin C A. Probability, Statistics, and Decisions for Civil Engineers[M]. New York: McGraw-Hill, 1970.
|
| [19] |
Montgomery D C, Runger G C, Hubele N F. Engineering Statistics[M]. New York: John Wiley & Sons, 2010.
|
| [20] |
闫澍旺, 朱红霞, 刘润. 关于随机场理论在土工可靠度计算中应用的研究[J]. 岩土工程学报, 2006, 28(12): 2053-2059. Yan Shuwang, Zhu Hongxia, Liu Run. Study on Application of Random Field Theory to Reliability Analysis[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(12): 2053-2059. DOI:10.3321/j.issn:1000-4548.2006.12.002 |
| [21] |
刘春原, 闫澍旺. 岩土参数随机场特性及线性预测[J]. 岩土工程学报, 2002, 24(5): 588-591. Liu Chunyuan, Yan Shuwang. Characteristic of the Random Field of Geotechnical Parameters and Linear Prediction[J]. Chinese Journal of Geotechnical Engineering, 2002, 24(5): 588-591. DOI:10.3321/j.issn:1000-4548.2002.05.010 |
| [22] |
冯波, 陈明涛, 岳冬冬, 等. 基于两种插值算法的三维地质建模对比[J]. 吉林大学学报(地球科学版), 2019, 49(4): 1200-1208. Feng Bo, Chen Mingtao, Yue Dongdong, et al. Comparison of 3D Geological Modeling Based on Two Different Interpolation Medthods[J]. Journal of Jilin University (Earth Science Edition), 2019, 49(4): 1200-1208. |
| [23] |
郑天成, 侯卫生, 何思彤. 基于二维地质剖面的三维地质结构多点统计学模拟方法[J]. 吉林大学学报(地球科学版), 2019, 49(5): 1496-1506. Zheng Tiancheng, Hou Weisheng, He Sitong. An MPS-Based Simulation Algorithm for 3D Geological Structure with 2D Cross-Sections[J]. Journal of Jilin University (Earth Science Edition), 2019, 49(5): 1496-1506. |


