2. 吉林大学地球探测科学与技术学院, 长春 130026
2. College of GeoExploration Science and Technology, Jilin University, Changchun 130026, China
0 引言
利用数值模拟方法研究不同介质中的井孔声场传播特征对于我们利用声波测井获取地层信息至关重要。针对各种地层介质的声场传播,首先需要将地层介质等效成各种数学物理模型,然后利用一定的数学方法进行计算。很多情况下,将地层视作理想弹性体,在一定程度上能够描述地下介质中波的传播。然而,研究[1]发现弹性波的衰减仍远大于球面扩散、透射等造成的机械能的损失。这是由于地层具有黏滞性,机械波在实际地层中传播伴随着地层黏滞性造成能量的耗散,因此,黏弹性理论能够更准确地描述地层中声场的传播,黏弹性介质模型更为贴近实际。
早在1845年,Stocks就对黏弹性流体中的声波传播进行了描述并建立了斯托克斯方程,随后,黏弹性介质受到关注并出现了一系列理论和研究方法。目前用于研究黏弹性介质的基本理论模型主要有3种[2]:一种是麦克斯韦尔黏弹性模型,该模型用一个弹簧和一个阻尼器(黏性元件)串联来表示其单元体;另一种是Kelvin-Voigt模型,将一个弹簧和一个阻尼器并联来表示其单元体,常用来描述黏滞性固体中的应力应变关系;还有一种称作标准线性固体模型以及由此推广得到的广义标准线性固体模型,标准线性固体模型是将单元体看作一个弹簧和一个Kelvin-Voigt模型相互串联组合而成,而广义标准线性固体模型是由多个标准线性固体模型并联而成。刘瑞珣等[3]指出,用Kelvin-Voig模型描述地下介质既简便又较为符合地下实际情况。
许多学者对黏弹性理论进行了大量的研究,并将其应用到地球物理的波场模拟计算当中。Emmerich等[4]对广义线性固体模型二维有限差分算法进行了研究;Robertsson等[5-6]利用广义标准线性体模型采用交错网格有限差分方法对地震波场进行了模拟;Saenger等[7]利用旋转交错网格有限差分法对黏弹性以及各向异性介质中的地震波场进行了模拟;Bai等[8]利用时间域有限差分算法对衰减各向异性黏弹性介质中的波场进了模拟。
国内学者也对黏弹性介质中的地震波场做了许多研究:杜启振等[9-10]对各向异性黏弹性介质进行了模拟;苑春方等[11]利用Kelvin-Voigt模型对黏弹性介质中的地震波进行了有限差分数值模拟;孙成禹等[12-13]研究了三参数常Q黏弹性模型构造方法,并对有限差分稳定性进行了分析;郭智奇等[14-15]对黏弹各向异性介质与储层信息做了深入研究;刘财等[16]将含有分数阶时间导数的常Q黏弹固体骨架各向异性本构关系及孔隙流体的黏滞性本构关系引入双相介质理论,并对其进行了有限差分数值模拟;邵广周等[17]利用Kelvin-Voigt模型采用交错网格有限差分方法对黏弹性介质中的面波进行了数值模拟;张壹等[18]对黏弹性介质中地震波的吸收衰减进了归纳。
黏弹性介质理论已经广泛应用于地震波场的模拟,而对于井孔声场来说,由于井眼内充满流体,井内接收到的波是经井壁滑行形成的折射波以及各种导波,井外地层传播的波是经过井壁多次反射和透射形成的波。因此,井孔声场的传播与地震中弹性波的传播有着明显的区别,对于黏弹性介质而言,井内外接收到的声波场的衰减与井外地层的性质有着密切关系。因此,研究井内外声场的传播与井外黏弹性介质的关系对利用声波测井信号获取地层信息非常重要,而目前对于这方面的研究还比较少见。笔者采用交错网格有限差分算法对Kelvin-Voigt黏弹性介质中的井孔声场进行数值模拟,研究黏弹性介质中井孔声场和井外地层中波的衰减特征。
1 Kelvin-Voigt黏弹性介质井中传播方程根据Kelvin-Voigt黏弹性单元体模型本构关系,对于各向同性介质,柱坐标系下的应力方程为:
 (1)
(1) 式中:r和z分别代表径向和垂向坐标;τrr、τzz分别为径向和垂向正应力;τrz为剪切应力;c11、c13、c33、c44为弹性常数;u和w分别为径向和垂向位移分量;c′11、c′13、c′33、c′44为黏滞性系数;t为时间。根据速度与应力的关系有
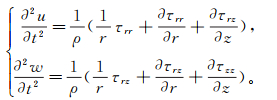 (2)
(2) 式中,ρ为介质密度。对式(1)中方程两边对时间求导可得:
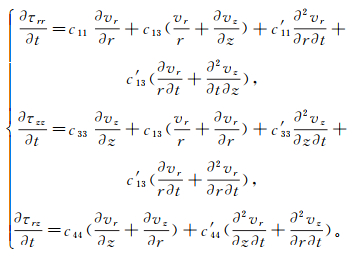 (3)
(3) 令
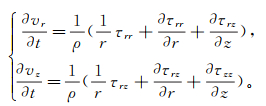 (4)
(4) 对于各向同性介质,c11、c13、c33、c44为4个独立的弹性常数:

式中:λ和μ为弹性介质Lamé参数;vP和vS分别为纵波和横波的速度。令λ′和μ′分别为λ和μ对应的黏滞性系数,则

式中:ω为角频率;QP和QS分别为纵、横波的品质因子。
2 柱坐标系下交错网格有限差分方程在二维柱坐标系下将方程(3)转化为差分方程。网格模型设置如下:径向步长设置为Δr,网格数为M;轴向步长设置为Δz,网格数为N;时间间隔设为Δt。高阶有限差分算子的优势在于其利用高阶差分算子近似空间导数。笔者在井孔超声波场离散的过程中空间上采用高阶差分算子,时间域导数仍采用二阶差分近似,同时采用交错网格技术以减少频散。将速度和应力分量离散化,令Ti, jk、Ri, jk、

 (5)
(5) 式中,Dr-、Dr+、Dz-、Dz+分别表示r、z方向一阶导数2L阶精度的向后、向前差分算子。假设变量用函数f表示,则f在r、z方向的差分算子可表示为:
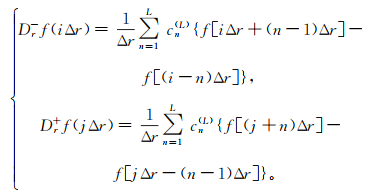 (6)
(6) 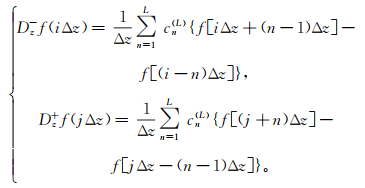 (7)
(7) 式中,cn(L)为差分系数,可通过下面的方程组求取:
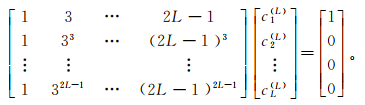 (8)
(8) 解方程组可得
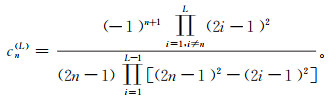 (9)
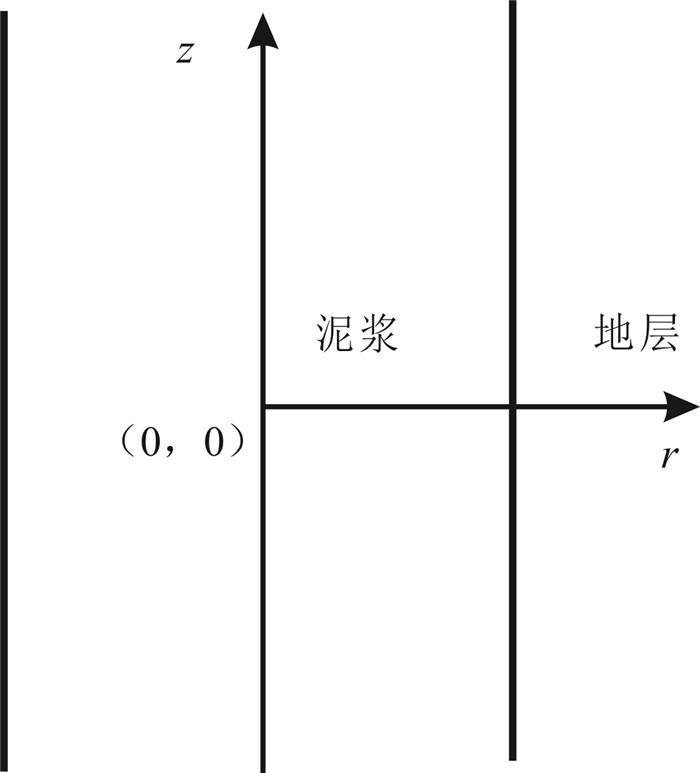
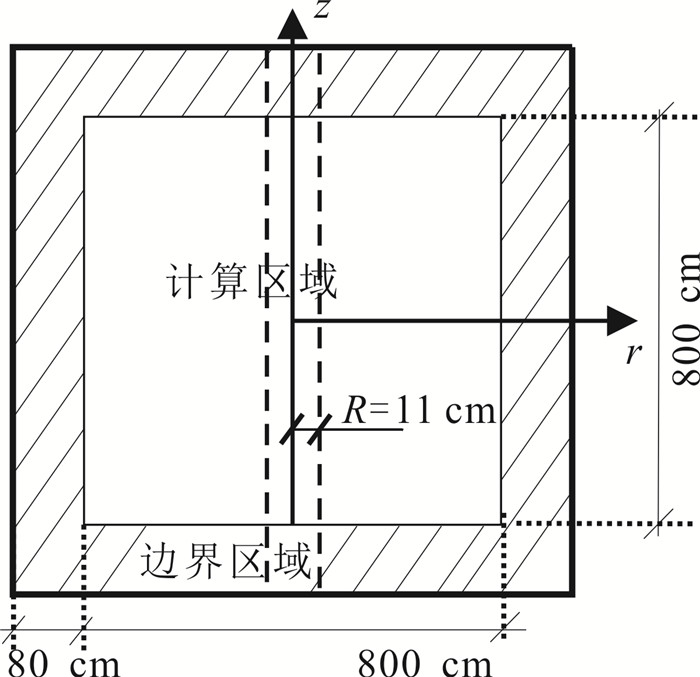
(9) 笔者分别对弹性介质、黏弹性介质1、黏弹性介质2、黏弹性介质3等4种不同地层介质(井内泥浆及井外介质参数如表 1所示)进行了数值模拟,Δr=Δz=0.01 m,Δt=1 μs。将井轴设为柱坐标z轴,竖直向上为正方向,水平方向为径向,声源位于坐标(0, 0)位置(图 1)。根据式(5)—(8),本文取L=5,即采用空间10阶、时间2阶,吸收边界采用完全匹配层[19](perfectly matched layer,PML)进行模拟计算。计算区域网格划分如图 2所示。吸收边界径向和轴向都为80 cm,计算区域为800 cm×800 cm,井半径R=11 cm。
| 介质 | ρ/(kg/cm3) | vP/(m/s) | vS/(m/s) | QP | QS |
| 井内泥浆 | 1 000 | 1 500 | — | — | — |
| 弹性介质 | 2 400 | 3 000 | 1 800 | — | — |
| 黏弹性介质1 | 2 400 | 3 000 | 1 800 | 60 | 40 |
| 黏弹性介质2 | 2 400 | 3 000 | 1 800 | 300 | 200 |
| 黏弹性介质3 | 2 400 | 3 000 | 1 800 | 1 500 | 1 000 |
|
| 图 1 井孔声场计算柱坐标系示意图 Fig. 1 Schematic cylindrical diagram of borehole acoustic field for calculation coordinate system |
|
|
|
| 虚线为井边界。 图 2 声场计算网格划分示意图 Fig. 2 Schematic diagram of borehole acoustic field for calculation meshgrids |
|
|
本文采用雷克子波函数作为声源时域函数,其函数形式如下:
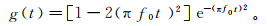 (10)
(10) 式中,f0为声源中心频率。
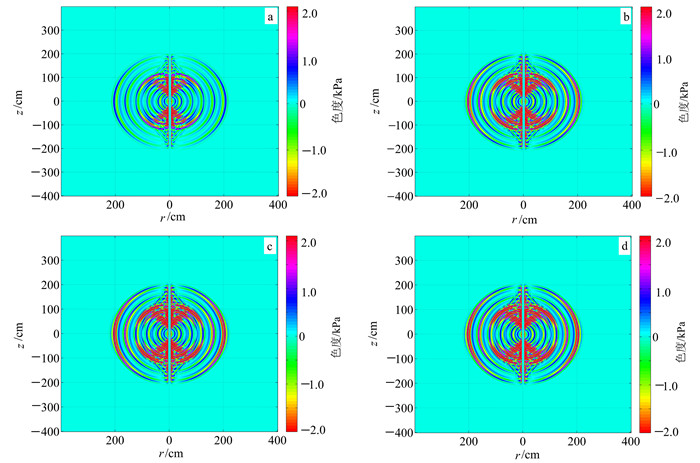
3.1 品质因子对井内外声场衰减的影响图 3为表 1中4种井外介质在t=800 μs时刻获得的井内外声场快照。从图 3中可以清晰地看出井孔声场传播波形。从波场传播区域来看,图 3a、b、c、d中首波传播的距离几乎相同;可见,品质因子对声波传播的速度几乎没有影响或影响很小。从波场传播区域的色度变化可以看出,声场振幅有明显区别,图 3a、b、c、d中的井外声场振幅依次增大;可见在其他条件不变的情况下,随着纵、横波品质因子的增大,井外声场衰减减小,振幅增大,而弹性波的振幅最大。
|
| a. 黏弹性介质1;b. 黏弹性介质2;c. 黏弹性介质3;d. 弹性介质。 图 3 不同介质在t=800 μs时刻获得的井内外声场快照 Fig. 3 Snapshots of the acoustic field inside and outside the well at t=800 μs in different media |
|
|
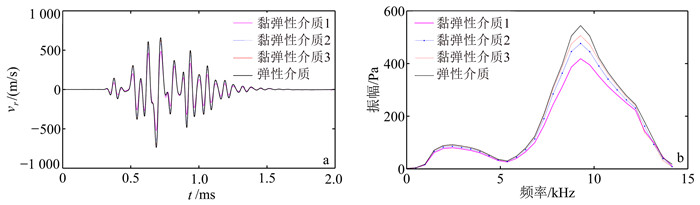
图 4a为4种不同井外介质源距为1.0 m井轴上一点接收到的随时间变化的波形,图 4b为4种波列信号对应的振幅谱。可以看出:首波到时基本相同(图 4a),可见品质因子对井内反射波的传播速度几乎没有影响;随着纵、横波的品质因子的增大,井内声波振幅增大,逐渐越趋近于弹性介质的井内声场(图 4b)。
|
| 图 4 不同介质中接收到的井孔声场波形(a)及其振幅谱(b) Fig. 4 Received acoustic waveforms (a) and their amplitude spectrums (b) in the borehole for different media |
|
|
综上所述,品质因子对黏弹性介质中的井内外声场均有影响,井外声场和井内声场的衰减均随品质因子的增大而减小,振幅随之增大。
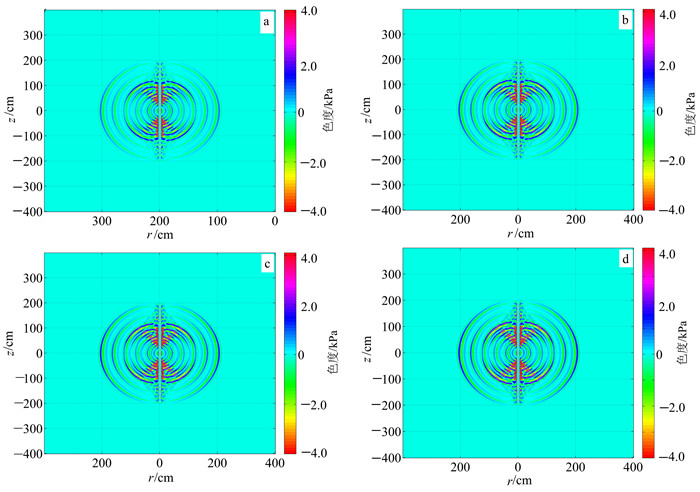
3.2 声源中心频率对井内外衰减的影响图 5为表 1中黏弹性介质1在声源中心频率分别为10、15、20、25 kHz、t=800 μs时刻获得的井内外声场快照。可以看出:首波传播的距离基本相同,可见声源中心频率对声波传播的速度影响很小;图 5a、b、c、d中井外声场振幅依次增大,可见随着声源中心频率的增大,井外声场的衰减减小。
|
| a. f=10 kHz; b. f=15 kHz; c. f=20 kHz; d. f=25 kHz。 图 5 黏弹性介质不同声源中心频率在t=800 μs时刻获得的井内外声场快照 Fig. 5 Snapshots of the acoustic field inside and outside the well at t=800 μs for different acoustic source center frequency |
|
|
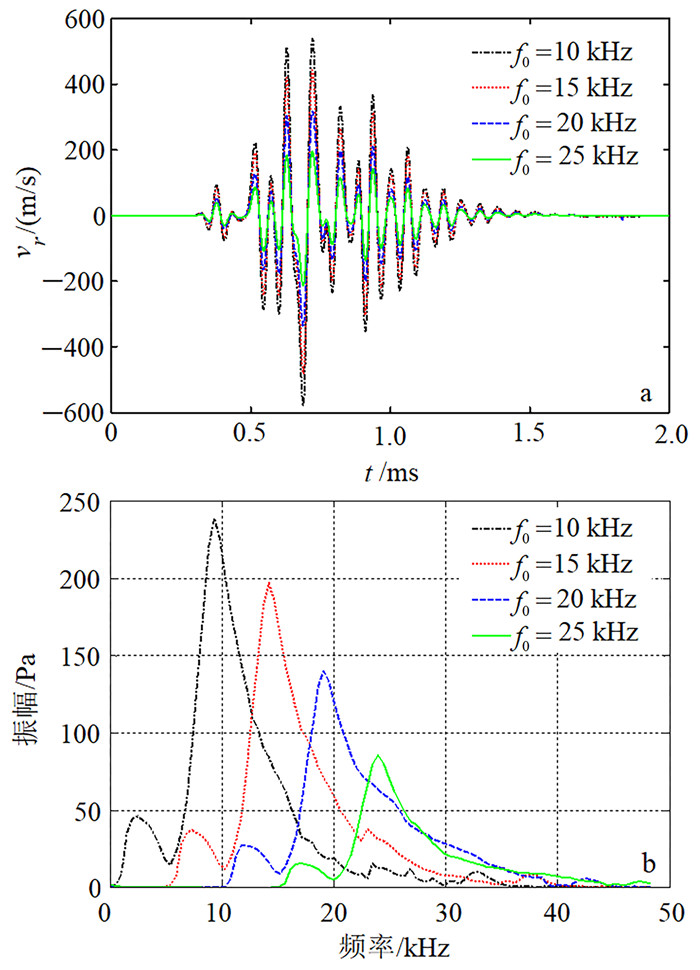
图 6a为不同声源中心频率源距为1.0 m井轴上一点接收到的随时间变化的波形,图 6b为其振幅谱。可以看出:首波到时相同(图 6a),可见声源中心频率对井内反射波的传播速度影响不大;随着声源中心频率增大,井内声场振幅减小,能量衰减增大。
|
| 图 6 黏弹性介质不同声源中心频率接收到的井孔声场波形(a)及其振幅谱(b) Fig. 6 Received acoustic waveforms (a) and their amplitude spectrums (b) in the borehole for for different acoustic source center frequency |
|
|
综上所述,声源中心频率对黏弹性介质中的井内外声场均有影响:井外声场的衰减随声源中心频率的增大而减小,振幅随之增大;井内声场的衰减随声源中心频率的增大而增大,振幅随之减小。
4 结论黏弹性介质模型能够准确地模拟井内外声场的传播特征。根据柱坐标系下Kelvin-Voigt模型的黏弹性波动方程,利用高阶交错网格有限差分法对井孔声场进行数值模拟,结果表明:
1) Kelvin-Voigt黏弹性介质模型相对于弹性介质模型增加了黏滞性系数,有利于研究声场在岩石介质中的衰减特征。
2) 品质因子对黏弹性介质中的井内外声场均有影响,井外声场和井内声场的衰减均随品质因子的增大而减小,振幅随之增大。
3) 声源中心频率对黏弹性介质中的井内外声场均有影响。井外声场的衰减随声源中心频率的增大而减小,振幅随之增大;井内声场的衰减随声源中心频率的增大而增大,振幅随之减小。
| [1] |
孙成禹. 地震波理论与方法[M]. 东营: 中国石油大学出版社, 2007. Sun Chengyu. Theory and Methods of Seismic Waves[M]. Dongying: China University of Petroleum Publishing House, 2007. |
| [2] |
Madja G, Chin R C Y, Followill F E. A Perturbation Theory for Love Waves in Anelastic Media[J]. Geophysical Journal of the Royal Astronomical Society, 1985, 80(1): 1-34. DOI:10.1111/j.1365-246X.1985.tb05076.x |
| [3] |
刘瑞珣, 张秉良, 张臣. 描述岩石黏弹性固体性质的开尔文模型[J]. 地学前缘, 2008, 15(3): 221-225. Liu Ruixun, Zhang Bingliang, Zhang Chen. The Kelvin Model Describing Rock Materials with Behaviour of a Viscoelastic Solid[J]. Earth Science Frontiers, 2008, 15(3): 221-225. DOI:10.3321/j.issn:1005-2321.2008.03.018 |
| [4] |
Emmerich H, Korn M. Incorporation of Attenuation into Time-Domain Computations of Seismic Wave Fields[J]. Geophysics, 1987, 52(9): 1252-1264. DOI:10.1190/1.1442386 |
| [5] |
Robertsson J O A, Blanch J O, Symes W W. Viscoelastic Finite-Difference Modeling[J]. Geophysics, 1994, 59(9): 1444-1456. DOI:10.1190/1.1443701 |
| [6] |
Robertsson J O A. A Numerical Free-Surface Condition for Elastic/Viscoelastic Finite-Difference Modeling in the Presence of Topography[J]. Geophysics, 1996, 61(6): 1921-1934. DOI:10.1190/1.1444107 |
| [7] |
Saenger E H, Bohlen T. Finite-Difference Modeling of Viscoelastic and Anisotropic Wave Propagation Using the Rotated Staggered Grid[J]. Geophysics, 2004, 69(2): 583-591. DOI:10.1190/1.1707078 |
| [8] |
Bai Tong, Tsvankin I. Time-Domain Finite-Difference Modeling for Attenuative Anisotropic Media[J]. Geophysics, 2016, 81(2): c69-c77. DOI:10.1190/geo2015-0424.1 |
| [9] |
杜启振, 杨慧珠. 线性黏弹性各向异性介质速度频散和衰减特征研究[J]. 物理学报, 2002, 51(9): 2101-2108. Du Qizhen, Yang Huizhu. Velocity Dispersion and Attenuation in Anisotropic Linear Viscoelastic Media[J]. Acta Physica Sinica, 2002, 51(9): 2101-2108. DOI:10.3321/j.issn:1000-3290.2002.09.035 |
| [10] |
杜启振. 各向异性黏弹性介质伪谱法波场模拟[J]. 物理学报, 2004, 53(12): 4428-4434. Du Qizhen. Wavefield Forward Modeling with the Pseudo-Spectral Method in Viscoelastic and Azimuthally Anisotropic Media[J]. Acta Physica Sinica, 2004, 53(12): 4428-4434. |
| [11] |
苑春方, 彭苏萍, 张中杰, 等. Kelvin-Voigt均匀黏弹性介质中传播的地震波[J]. 中国科学: D辑: 地球科学, 2005, 35(10): 957-962. Yuan Chunfang, Peng Suping, Zhang Zhongjie, et al. Seismic Wave of Propagation in Homogeneous Kelvin-Voigt Viscoelastic Medium[J]. Science in China: Series D: Earth Sciences, 2005, 35(10): 957-962. |
| [12] |
孙成禹, 印兴耀. 三参数常Q黏弹性模型构造方法研究[J]. 地震学报, 2007, 29(4): 348-357. Sun Chengyu, Yin Xingyao. Construction of Constant-Q Viscoelastic Model with Three Parameters[J]. Acta Seismologica Sinica, 2007, 29(4): 348-357. DOI:10.3321/j.issn:0253-3782.2007.04.002 |
| [13] |
孙成禹, 肖云飞, 印兴耀, 等. 黏弹介质波动方程有限差分解的稳定性研究[J]. 地震学报, 2010, 32(2): 147-156. Sun Chengyu, Xiao Yunfei, Yin Xingyao, et al. Study on the Stability of Finite Difference Solution of Visco-Elastic Wave Equations[J]. Acta Seismologica Sinica, 2010, 32(2): 147-156. |
| [14] |
郭智奇. 黏弹各向异性介质波场模拟与储层信息研究[D]. 长春: 吉林大学, 2008. Guo Zhiqi. Wave Field Modeling in Viscoelastic Anisotropic Media and Reservoir Information Study[D]. Changchun: Jilin University, 2008. |
| [15] |
Guo Zhiqi, Liu Xiwu, Fu Wei, et al. Modeling and Anlysis of Azimuthal AVO Responses from a Viscoelastic Anisotropic Reflector[J]. Applied Geophysics, 2015, 12(3): 441-452. DOI:10.1007/s11770-015-0498-9 |
| [16] |
刘财, 胡宁, 郭志奇, 等. 基于分数阶时间导数常Q黏弹本构关系的含黏滞流体双相VTI介质中波场数值模拟[J]. 地球物理学报, 2018, 61(6): 2446-2458. Liu Cai, Hu Ning, Guo Zhiqi, et al. Numerical Simulation of the Wavefield in a Viscous Fluid-Saturated Two-Phase VTI Medium Based on the Constant-Q Viscoelastic Constitutive Relation with a Fractional Temporal Derivative[J]. Chines Journal of Geophysics, 2018, 61(6): 2446-2458. |
| [17] |
邵广周, 赵凯鹏, 吴华. 基于MPI的面波有限差分正演模拟[J]. 吉林大学学报(地球科学版), 2020, 50(1): 294-303. Shao Guangzhou, Zhao Kaipeng, Wu Hua. Finite Difference Forward Modeling of Surface Waves Based on MPI[J]. Journal of Jilin University (Earth Science Edition), 2020, 50(1): 294-303. |
| [18] |
张壹, 王赟, 王祥春, 等. 黏弹性介质地震波吸收衰减研究进展[J]. 石油物探, 2021, 60(2): 238-250. Zhang Yi, Wang Yun, Wang Xiangchun, et al. Research Progress on the Absorption Attenuation of Seismic Waves in Viscoelastic Media[J]. Geophysical Prospecting for Petroleum, 2021, 60(2): 238-250. DOI:10.3969/j.issn.1000-1441.2021.02.005 |
| [19] |
Alford R M, Kelly K R, Boore D M. Accuracy of Finite-Difference Modeling of Acoustic Wave Equation[J]. Geophysics, 1974, 39(6): 834-842. DOI:10.1190/1.1440470 |


