0 引言
由于海面是强反射界面,地震波传播至海面时易发生二次反射。我们把检波器接收的二次反射称作多次波[1]。多次波的动力学、运动学特征与发育层位的一次波相近,在地震数据中表现为强相干性,与中深层一次波同相轴耦合,极大增加了地震成像和解释的难度。在海洋地震数据处理流程中,多次波压制问题一直是研究重点[2]。
根据基本假设不同,现存的多次波压制方法可分为基于差异的滤波方法和基于波动方程的预测减去法[3]。基于差异的滤波方法利用一次波与多次波的运动学特征,设计适当的滤波器实现多次波压制。主要包括:预测反褶积、f-k滤波、抛物Radon变换滤波等[4]。基于波动方程的方法根据多次波发育的周期性,利用波动方程模拟多次波传播过程,进而实现多次波的压制。主要包括:逆散射级数法、反馈迭代法等[1, 5]。基于勘探目标复杂化的大背景,波动方程类方法的预测精度更高,在复杂条件下优势明显。目前,业界广泛采用的多次波压制方法是SRME(surface-related multiple elimination)方法[2-3]。该方法是反馈迭代法的一种,将多次波压制过程分为多次波预测和自适应减去两步,通过自身数据褶积进行多次波预测。预测结果的旅行时虽然准确,但其振幅、相位特征与实际多次波存在较大误差,需要设计自适应滤波器匹配误差,其匹配精度决定了最终的多次波压制效果。
目前工业界普遍采用的自适应匹配减去方法是Guitton等[6]基于能量最小原则提出的匹配方法。该方法要求一次波与多次波具有正交性,即两者不存在同相轴交叉现象。但在地震波复杂的传播过程中,一次波与多次波的耦合无法避免。因此,该方法在一次波与多次波交叉位置的适用性降低,无法在多次波压制效果良好的同时兼顾一次波的保幅性。由于匹配过程在局部窗口中进行,考虑全局压制结果,统一的匹配参数易在局部窗口出现一次波损伤、多次波残留等问题[7]。为提升同相轴交叉位置的匹配精度,现有方法主要利用稀疏变换的稀疏性对地震数据进行稀疏表示,进而提升匹配减去效果。Herrmann等[8]提出了基于Curvelet变换的多次波匹配方法,该方法将原始数据映射到Curvelet域,并对Curvelet系数进行匹配,通过增加输入数据的稀疏性提升匹配过程的效果和鲁棒性。基于Curvelet域匹配减去方法,Herrmann等[9]引入软阈值函数进行多次波减去,最大程度地避免一次波损伤,提升多次波压制方法的保幅性。Wang等[10]采用贝叶斯理论替代软阈值减去方法,进一步解决弱振幅一次波损伤和高频残留问题。王德利等[11-12]将Curvelet域匹配减去方法应用到层间多次波和三维多次波压制中。刘成明等[13]采用稀疏性更佳的Shearlet变换进行多次波匹配减去,进一步提升减去效果。但稀疏变换法在提升稀疏度的同时,极大增加了待匹配数据的空间维度,使得多次波匹配过程变为了超大尺度矩阵运算,这无疑增加了巨大的计算成本。
受稀疏表示(sparse representation)和压缩感知(compressed sensing)理论的推动,低秩表示(low-rank representation)的相关理论不断完善。低秩表示理论将矩阵的秩定义为定量测量矩阵相干性的工具。其核心思想是利用数据矩阵间的潜在相关性,自适应地剔除冗余信息,实现数据降维的目的[14]。2011年起,低秩表示理论由于性能优越和实现简便,受到地球物理学家的关注,在数据重构[15]、随机噪声压制[16]、相干噪声压制[17]、混采噪声分离[18]、偏移成像[19]等领域均取得了一系列成果。在大多数情况下,低秩逼近方法可获得良好的效果,尤其是针对地下结构相对平坦的叠后资料。低秩表示的基本假设是地震数据仅包含若干个线性同相轴,则该数据对应的数据矩阵具有低秩特性,进而可用该矩阵的秩表征同相轴的倾角分量数。但当地下结构复杂时,数据矩阵的秩骤增,低秩参数将难以选择[20]。为提升低秩表示方法对复杂资料的适用性,通常在局部窗口中进行低秩表示。在局部窗口中,地震同相轴可近似看作线性的,但由于各窗口内倾角分量数目不一致,导致无法保证每个局部窗口的低秩参数最佳。
针对多次波匹配减去过程中交叉同相轴匹配难度大的问题,本文在前人研究的基础上,提出了基于经验低秩表示的自适应多次波减去方法:首先,将匹配减去方法转换到共偏移距道集中进行,以保证匹配道集的倾角相对平缓;其次,在低秩表示方法中引入经验模态分解(empirical mode decomposition,EMD)方法,优化低秩表示过程中局部窗口的参数选择问题,并将地震数据分解为倾角不同的低秩倾角分量;最后,在不同低秩倾角分量中分别采用基于能量最小原则的匹配减去方法,并重构各分量,得到最终减去结果。经验低秩表示方法将地震数据自适应地分解为信噪比高、倾角单一、同相轴相位圆滑的低秩倾角分量。根据以上特性,本文方法通过解决匹配过程中的同相轴交叉问题,以扩大常规减去方法的使用范围,使得本文方法可兼顾计算效率和多次波压制效果。本文利用提出的算法进行了有效性和抗噪性测试,证明了方法的优越性。
1 算法原理和实现 1.1 主成分分析和低秩表示主成分分析是统计学中多元分析的重要工具。其核心思想是在减少数据集维数的同时,尽可能保留数据变量的可变性[21]。假设数据矩阵D由信号分量S、随机噪声Nr和相干噪声Nc组成:
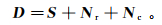 (1)
(1) Nr+Nc可以概括为噪声分量N。假设N由小振幅的随机扰动组成,则可以通过以下优化问题得到S的最优估计:
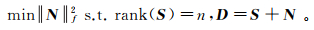 (2)
(2) 式中:Srank表示矩阵的秩;n为应用于目标数据的低秩参数;f为输入矩阵的Frobenius范数。该问题可以通过奇异值分解方法(singular value decomposition, SVD)[22]有效解决。SVD是特征分解在任意矩阵上的推广,其目的是提取数据矩阵中最重要的特征。观测数据矩阵D可以通过SVD分解为一组特征值序列。如果观测数据矩阵的奇异值主要集中在几个有限的元素上,并且有少数的奇异值远远大于其他的奇异值,则该矩阵可以近似看作低秩的[23]。当地震数据仅包含若干个线性同相轴时,噪声和有效信号的相关性差异大,观测矩阵D可近似看作是低秩矩阵[20]。其信号分量S的奇异值主要集中在几个有限的元素上,而噪声分量N的奇异值分布在所有特征值序列,即可通过保留有限个振幅较大的奇异值构建低秩特征值序列,并利用该序列来描述信号分量S。这种方法称为低秩表示法,其详细流程如下:
1) 计算D的SVD分解结果,SVD算法可将D分解为3个矩阵的乘积:
 (3)
(3) 式中:U和V为正交矩阵;Σ为对角矩阵。若D的矩阵维度为M×N,则U和V的维度分别为M×M和N×N。Σ可表示为
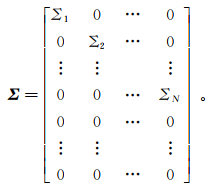 (4)
(4) 式中,对角线元素Σi(i≤N)表示D的奇异值,且满足∣Σ1∣≥∣Σ2∣≥…≥∣ΣN∣。
2) 选择Σ中m个最大对角元素并将其他元素充零,以计算低秩近似奇异值矩阵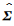
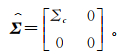 (5)
(5) 式中,Σc=Σ1∶m, 1∶m。一般情况下,m≪N,可用振幅大小前1%的对角线元素近似表示数据矩阵。
3)计算低秩表示的数据矩阵
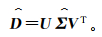 (6)
(6) 为了创建具有低秩特征的数据格式,首先需要将地震数据映射到Hankel矩阵[18],然后采用上文介绍的低秩近似方法进行处理。以在规则网格上采集的二维地震数据为例,任一频率切片D(x, ω) (x表示道号,x=1, 2, …, X, X表示道数; ω表示频率)的Hankel矩阵结构为
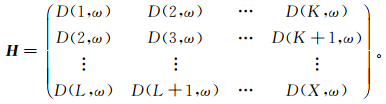 (7)
(7) 式中: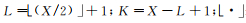
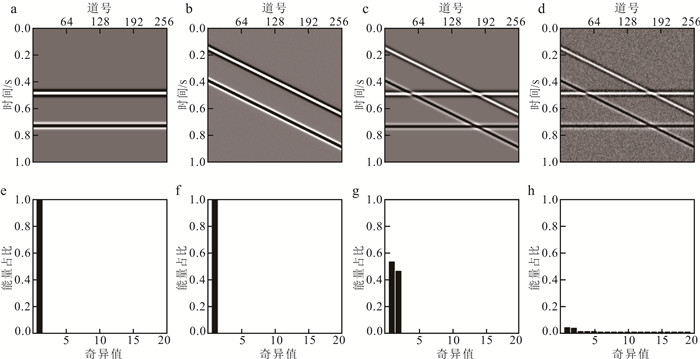
为了明确低秩矩阵的奇异值分布特征,本文建立了4个倾角不同、信噪比不同的线性同相轴模型(图 1a—d),详细参数见表 1。模型采样点数为256,分析窗口L=128(采用较大分析窗口可获得更多的奇异值),按振幅大小的顺序,保留前20个奇异值以研究不同模型的奇异值分布特征(图 1e—h)。本文将振幅明显大于0的奇异值定义为有效奇异值,对比图 1各图可看出:1)针对高信噪比数据(图 1a—c),有效信号的能量集中在若干有效奇异值上,可将其视为低秩矩阵(图 1e—g);2)针对高信噪比数据,有效奇异值数与同相轴数无关,与独立倾角数有关(图 1e、f);3)针对高信噪比数据,独立倾角数的增加会使有效奇异值数增加,且有效奇异值数等于独立倾角数(图 1f、g);4)针对低信噪比数据,由于噪声的存在,奇异值能量分布较分散,不具备低秩特性(图 1h)。因此,如果局部窗口包含独立倾角的j个平面波,H的秩为j。添加其他倾角平面波或随机噪声将增加Hankel矩阵的秩。因此,可以通过对H进行降秩以实现波场分解或噪声压制。
|
| 图 1 倾角不同、信噪比不同模型的奇异值分布特征 Fig. 1 Singular value distribution of models with different dip angles and SNR |
|
|
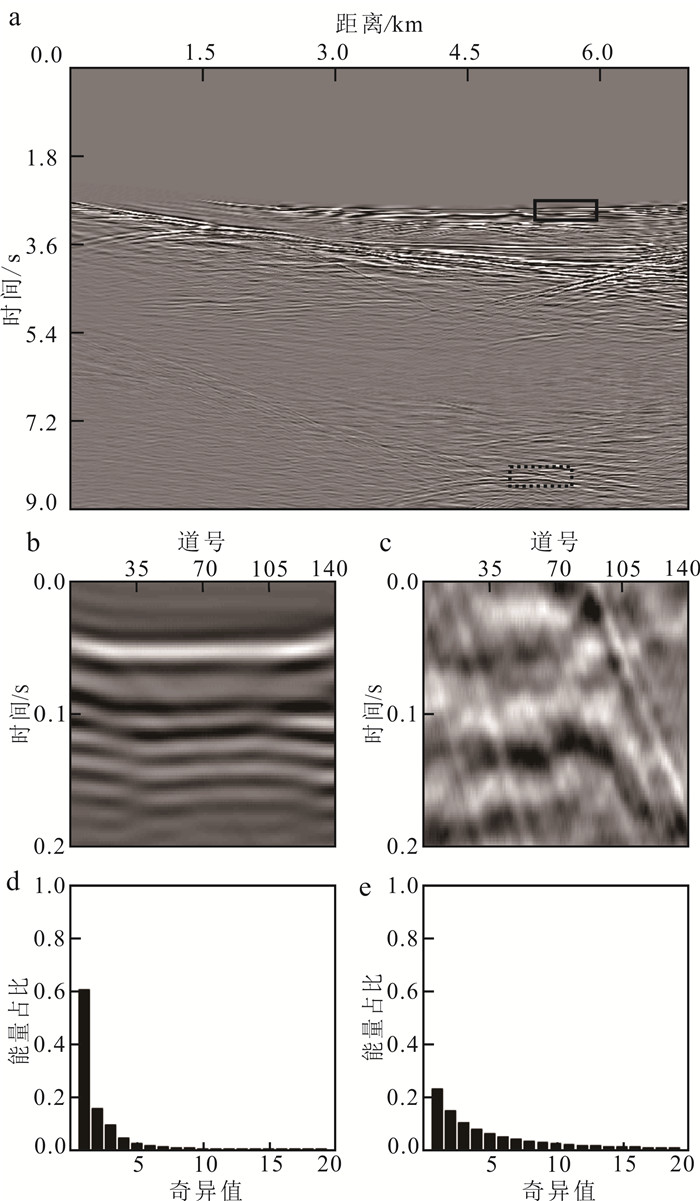
实际地震数据中不仅包含线性同相轴,同样包含弯曲同相轴,为了使低秩表示方法在实际地震数据处理中具有鲁棒性,通常采用局部窗口的方式处理。在局部窗口中,地震同相轴可近似视为线性同相轴,即窗口内有效信号具有低秩特性。基于局部窗口处理的低秩表示方法虽已广泛应用于地震数据处理领域,但是,该方法仍然存在一些问题。最大的问题之一是局部窗口的低秩参数选择不一致,即不同局部处理窗口中的秩不同。为明确实际资料中倾角差异与秩的关系,本文分析了某实际资料不同窗口的奇异值分布特征(图 2)。图 2a展示了该资料的叠后剖面,窗口尺寸为100×150,实线方框区域同相轴倾角相对一致,而虚线方框区域同相轴倾角差异较大。从图 2b、d可看出,实际资料局部窗口的同相轴仍有一定弯曲程度,导致窗口的秩增高,但主要奇异值能量仍集中在有限个奇异值中,仍具有低秩特性,满足低秩表示方法的适用条件。倾角差异和秩的关系与线性同相轴模型相似:当倾角一致时,该区域的秩较低(图 2b、d);当倾角差异较大时,该区域的秩较高(图 2c、e)。这意味着不同局部窗口无法采用全局的低秩参数进行处理:如果全局低秩参数设置太小,则复杂局部处理窗口的数据会严重损坏;而当全局低秩参数设置太大时,局部低秩表示方法无法完整剔除冗余信息。
|
| a. 实际地震数据中的秩;b. 浅层窗口(图 2a中实线);c. 深层窗口(图 2a中虚线);d. 浅层窗口奇异值分布;e. 深层窗口奇异值分布。 图 2 实际地震数据中的秩不一致 Fig. 2 Demonstration of the rank inconsistency in field seismic data |
|
|
由于地震数据具有空间各向异性,局部处理窗口的倾角分量存在扰动。由上文可知,数据矩阵内独立倾角分量数与该矩阵的秩相等,因此,倾角分量的扰动直接导致输入数据的秩无法统一,即局部窗口低秩参数选取困难。为解决这一问题,首先将存在扰动的输入数据分解为更平稳的倾角分量,以保证每个分解分量Hankel矩阵的低秩参数一致。实际地震资料的数据量十分庞大,为保证运算效率,该分解过程应该是自适应的。EMD可自适应地将非平稳数据分解为有限的本征模态函数(IMF),且本征模态函数是局部平稳的[24]。非平稳信号在频率-空间域的EMD分解可视为倾角分解,经验低秩表示方法首先采用频率-空间域EMD算法将地震数据分解为各自独立的倾角分量,通过减少局部窗口的倾角扰动,对所有局部处理窗口的IMF使用相同的低秩参数,简化常规低秩表示方法的参数选择过程[25]。
由图 1分析可知,当输入数据信噪比较高时,有效信息的能量集中在若干有效奇异值上,因此,有效信号对应奇异值的振幅远大于噪声对应奇异值的振幅。本文按照奇异值梯度最大原则自适应选择低秩参数:
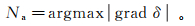 (8)
(8) 式中:Na为低秩参数;δ为Hankel矩阵对应的奇异值序列。
1.3 基于经验低秩表示的自适应多次波减去如上文所述,SRME方法的预测结果与实际多次波在振幅、相位特征上存在较大误差,需要自适应滤波器进行匹配以补偿误差。自适应滤波器可表示为
 (9)
(9) 式中:p(t)为多次波压制结果;d(t)为原始地震数据;m(t)为多次波预测模型;f(t)为自适应滤波器;*表示褶积。
假设多次波压制结果能量最小[26],构建基于L2范数的目标函数E(f),即
 (10)
(10) 最小。根据最小二乘反演思想,将能量最小问题转化为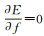
由上文可知,经验低秩表示方法将地震数据自适应地分解为若干个独立倾角分量,针对不同分量,分别进行自适应减去,并对减去结果进行重构可达到优化自适应减去方法的目的,其目标函数为
 (11)
(11) 式中,k为局部处理窗口的低秩分量数。
图 3展示了基于经验低秩表示自适应减去方法的基本思想:在局部窗口中,利用经验低秩表示方法对原始数据、预测多次波进行低秩倾角分解; 通过分解改善数据矩阵的同相轴交叉现象,选择减去性能更高的匹配减去参数。
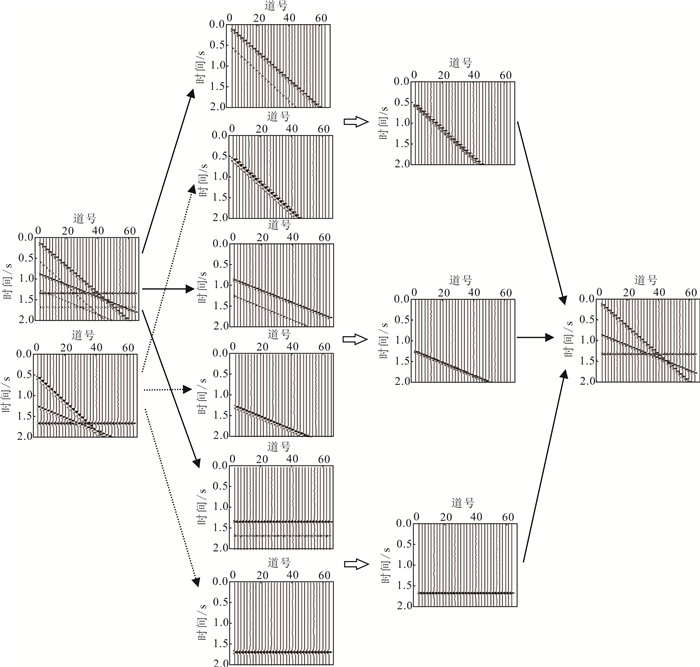
|
| 图 3 基于经验低秩表示的自适应多次波减去流程 Fig. 3 Workflow of the adaptive subtraction based on empirical low-rank representation |
|
|
该方法的完整流程如下。
1) 将原始数据和预测多次波作为输入数据。
2) 设置滑动窗口尺寸,并按局部窗口的方式处理:
a.将窗口数据从t-x转换为f-x域;
b.将EMD应用于窗口数据的每个频率切片以获得不同倾角的经验频率分量;
c.为每个频率切片的经验频率分量构造Hankel矩阵;
d.将SVD应用于Hankel矩阵以进行低秩表示;
e.通过沿对角线取平均值,将Hankel矩阵分解为不同经验分量;
f.将不同经验分量从f-x转换回t-x域,获得窗口数据的低秩倾角分量;
g.将基于能量最小原则的自适应匹配方法应用于各低秩倾角分量;
h.将不同分量的匹配结果进行求和,与原始数据做差,以输出局部处理窗口的减去结果。
3) 循环局部处理窗口,完成原始数据多次波减去过程。
2 应用实例采用理论和实际数据测试以验证本文提出方法在多次波减去中的有效性。在理论测试中,利用有限差分法对Pluto模型(图 4)进行正演模拟,获得理论数据。该数据包含400炮集,炮间距为15.24 m,每个炮集包含400道地震记录,最小偏移距0 m,道间距15.24 m,采样时间7.5 s,采样间隔0.004 s。实际数据包含300炮集,炮间距50 m,每个炮集包含480道地震记录,最小偏移距137.5 m,道间距12.5 m,采样时间9 s,采样间隔0.002 s。
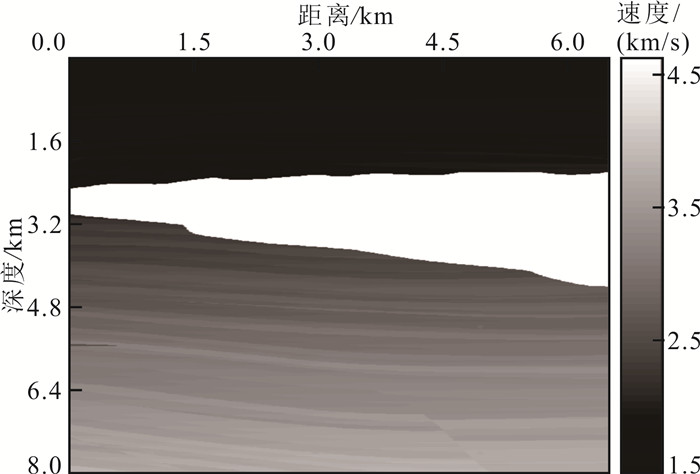
|
| 图 4 Pluto模型 Fig. 4 Pluto model |
|
|
在理论和实际试算过程中,对照组采用常规多次波减去方法,减去过程采用相同的多次波模型,从炮集、偏移距道集两方面对比减去结果,以证明本文提出方法的有效性。
2.1 理论数据试算图 5展示了原始数据的第300炮集和零偏移距道集。由于Pluto模型在深度2 500~4 500 m处存在高速层,高速层顶底界面的波阻抗差大,导致一次波振幅与多次波振幅差异较大。图 5b箭头指示了数据中发育的主要多次波,可看出3.1~3.9 s处多次波振幅弱,且与一次波耦合严重,在多次波匹配减去过程中需兼顾保幅性和分离性。

|
| a. 第300炮炮集;b.零偏移距道集。 图 5 理论数据的不同道集 Fig. 5 Different gathers of the synthetic data |
|
|
图 6展示了第300炮数据的多次波减去结果。图 6a为预测多次波,对比原始数据(图 5b)可看出两者在振幅和相位上存在差异,需进行自适应匹配减去。图 6b、c表示多次波减去结果,对比箭头位置可看出本文方法减去更彻底。图 6d、e表示原始数据与减去结果的差,即实际减去的多次波,对比两者可看出:本文方法减去的多次波波形稳定、保幅性好;常规方法减去的多次波中包含陡倾角信息,经对比预测多次波模型不包含该信息,因此判断该信息为原始数据中的一次波,即减去过程存在一次波损伤现象(图 6d虚线圆框、箭头处,虚线圆框位置振幅较弱,损伤更为严重)。
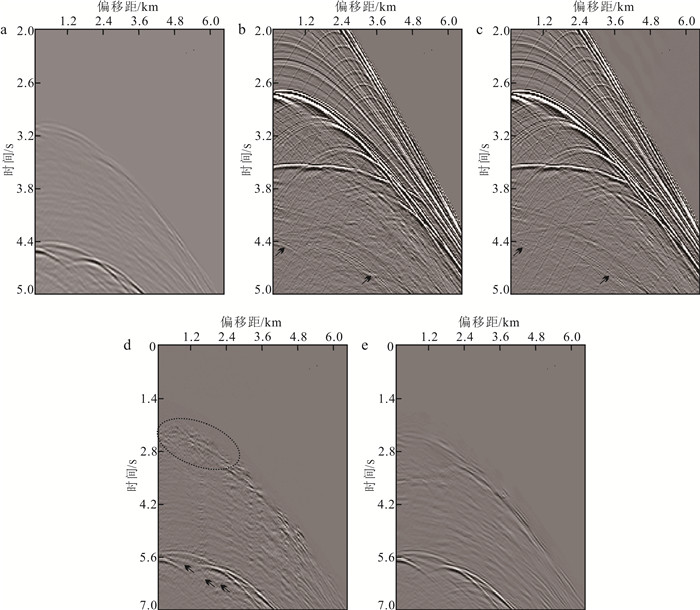
|
| a. 预测多次波模型;b. 常规方法减去结果;c. 本文方法减去结果;d. 常规方法减去多次波;e. 本文方法减去多次波。 图 6 理论数据第300炮炮集多次波减去结果 Fig. 6 Multiple subtraction of the 300th synthetic shot gathers |
|
|
图 7展示了零偏移距道集的多次波减去结果。图 7a展示了SRME方法预测的多次波模型,图 7b、c箭头位置指示了常规方法存在明显的多次波残留,图 7d、e虚线圆框、箭头位置指示了常规方法结果中存在一次波损伤现象。即零偏移距道集的多次波减去结果得到了与炮集结果相似的结论,本文方法的减去结果分离度高、保幅性好。
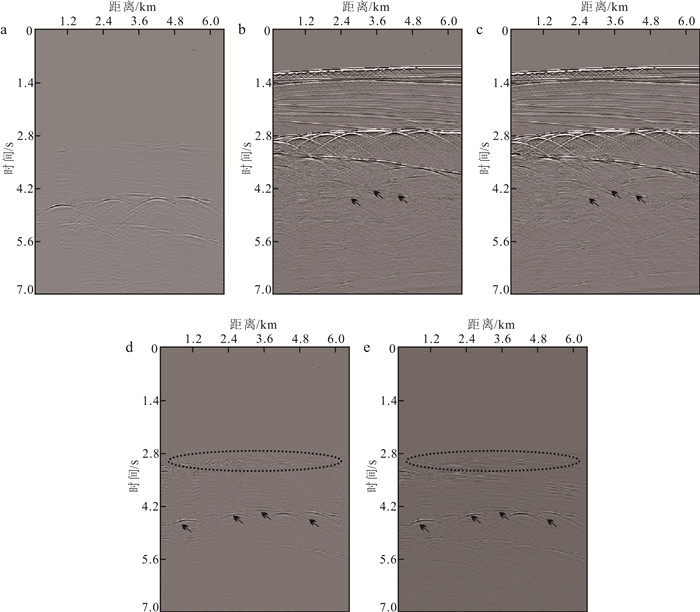
|
| a. 预测多次波模型;b. 常规方法减去结果;c. 本文方法减去结果;d. 常规方法减去多次波;e. 本文方法减去多次波。 图 7 理论数据零偏移距道集多次波减去结果 Fig. 7 Multiple subtraction of the synthetic zero-offset gathers |
|
|
炮集、零偏移距道集的减去结果证明了本文方法的有效性和优势。通过分析两道集的减去多次波,可以看出一次波损伤现象主要发生在一次波、多次波交叉区域。为避免减去过程损伤一次波,常规方法一般采用扩大匹配窗口、调节匹配减去参数等方式,这些方式无疑降低了减去方法的匹配性能。本文方法通过经验低秩表示有效避免了一次波、多次波交叉现象,可降低多次波匹配难度,且在窗口不变的条件下,选择性能更好的匹配减去参数。
2.2 实际数据试算为了进一步验证本文方法的有效性,选取某区域海洋实测地震数据进行试算。由图 8可知,由于地下结构复杂,地层倾角变化大,数据信噪比低,且多次波发育成因复杂,中深层一次波与干扰波场耦合严重,影响后续地震成像和解释对地层走势的判断。为实现中深层精确成像和解释,需获得分离度高的减去结果。
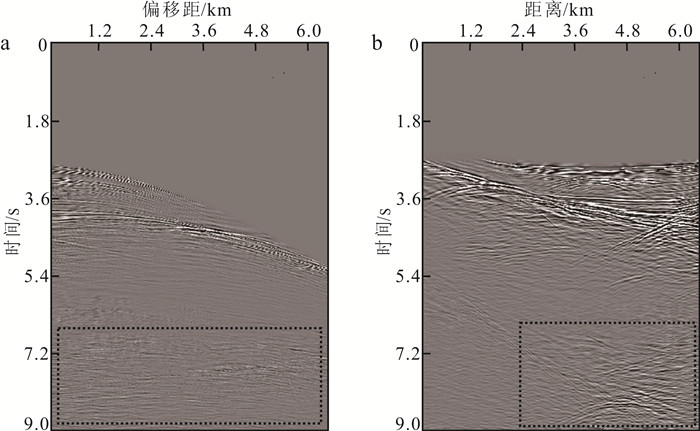
|
| a. 第140炮炮集;b.零偏移距道集。 图 8 实际数据的不同道集 Fig. 8 Different gathers of the field data |
|
|
图 9展示了炮集数据的多次波减去结果。从常规结果可明显看出,由于匹配减去参数调整,多次波减去更彻底,但同相轴连续性不佳,同时出现过匹配现象。本文结果在减去多次波的同时保持了同相轴连续性,远偏移距位置同相轴(虚线圆圈)在多次波减去后更清晰。

|
| a. 预测多次波模型;b. 常规方法减去结果;c. 本文方法减去结果。 图 9 实际数据炮集多次波减去结果 Fig. 9 Multiple subtraction of the field shot gathers |
|
|
图 10展示了多次波减去结果的叠加剖面。对比减去结果可明显看出,常规方法的叠加剖面仍可观察到多次波残留,本文方法的叠加剖面减去结果多次波减去彻底、同相轴连续、信噪比高。

|
| a. 预测多次波模型;b. 常规方法减去结果;c. 本文方法减去结果。 图 10 实际数据多次波减去结果对应叠加剖面 Fig. 10 Stack section of field data multiple subtraction |
|
|
通过对比图 9、图 10可知,本文方法处理结果中的中深层多次波减去更彻底,远偏移距位置一次波信息保幅性更好。本文方法更适合处理同相轴交叉的多次波减去问题,在实际数据中,多次波发育更复杂,同相轴交叉现象更易出现,因此本文方法处理实际数据更具优势。
3 讨论在验证本文方法的有效性后,我们对其抗噪性进行讨论。将强随机噪声加入线性同相轴模型(图 11a),使原始数据信噪比达到2.0(图 11b),采用常规方法和本文方法分别进行多次波减去试算,对比两方法在强噪声水平的性能。需注意,多次波预测过程为多道集褶积、叠加过程,对噪声有一定压制效果,因此在减去过程中,在预测多次波模型中未加噪。
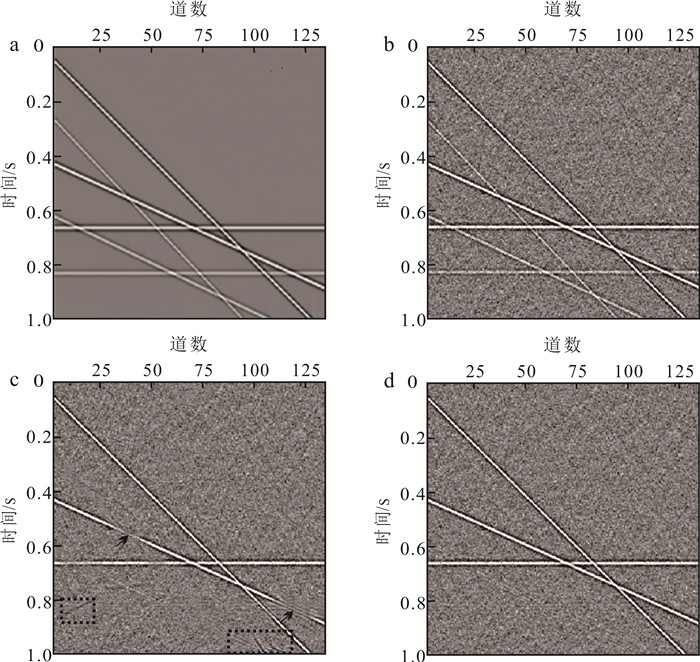
|
| a. 原始数据;b. 含噪数据;c. 常规方法减去结果;d. 本文方法减去结果。 图 11 抗噪性测试结果 Fig. 11 Noise sensitivity example |
|
|
图 11c为常规减去结果。可以看出,由于数据相对简单,减去结果在无同相轴交叉位置表现良好,但在同相轴交叉位置出现过匹配,甚至错匹配现象,即一次波损伤(箭头)和虚假同相轴(虚线框)。这表明当噪声水平高时,常规减去方法性能受限。
图 11d为本文方法减去结果。可以看出,本文方法在同相轴交叉位置优势明显,未出现一次波损伤现象,证明了本文方法的抗噪性更优异。其主要原因为经验低秩表示对含噪数据降秩的过程可剔除冗余信息,可理解为包含噪声压制功能的减去方法。
综上所述,本文方法的优势在于同相轴交叉情况的减去和抗噪性。随着地震勘探向复杂化发展,崎岖海底、坡折带等地层复杂区域越来越受到关注,本文方法更适合解决复杂区域的多次波压制问题。
4 结论1) 本文将匹配减去方法转换到共偏移距道集进行,并在低秩表示方法中引入经验模态分解方法,将地震数据分解为倾角不同的低秩倾角分量,在不同低秩倾角分量中分别采用常规基于能量最小原则的匹配减去方法,最终解决了多次波匹配减去过程中交叉同相轴匹配难度大的问题。
2) 综合理论、实际算例和抗噪性测试结果,本文方法在同相轴交叉、低信噪比情况下具有优势,对复杂条件下的实际数据同样适用,工业化价值高。
| [1] |
Verschuur D J, Berkhout A J, Wapenaar C P A. Adaptive Surface-Related Multiple Elimination[J]. Geophysics, 1992, 57(9): 1166-1177. DOI:10.1190/1.1443330 |
| [2] |
Berkhout A J, Verschuur D J. Estimation of Multiple Scattering by Iterative Inversion: Part I: Theoretical Considerations[J]. Geophysics, 1997, 62(5): 1586-1595. DOI:10.1190/1.1444261 |
| [3] |
Verschuur D J. Estimation of Multiple Scattering by Iterative Inversion: Part Ⅱ: Practical Aspects and Examples[J]. Geophysics, 1997, 62(5): 1596-1611. DOI:10.1190/1.1444262 |
| [4] |
Foster D J, Mosher C C. Suppression of Multiple Reflections Using the Radon Transform[J]. Geophysics, 1992, 57(3): 386-395. DOI:10.1190/1.1443253 |
| [5] |
石颖, 刘洪, 历玉英. 逆数据域表面多次波压制方法[J]. 吉林大学学报(地球科学版), 2011, 41(1): 271-276. Shi Ying, Liu Hong, Li Yuying. Inverse Data Domain Surface Multiple Suppression Method[J]. Journal of Jilin University (Earth Science Edition), 2011, 41(1): 271-276. |
| [6] |
Guitton A, Verschuur D J. Adaptive Subtraction of Multiples Using the L1-Norm[J]. Geophysical Prospecting, 2004, 52(1): 27-38. DOI:10.1046/j.1365-2478.2004.00401.x |
| [7] |
孙成禹, 谢俊法, 张立, 等. 利用多次波和二维匹配滤波的近偏移距数据重构方法[J]. 吉林大学学报(地球科学版), 2017, 47(1): 224-233. Sun Chengyu, Xie Junfa, Zhang Li, et al. Near-Offset Data Reconstruction Method Using Multiple Wave and Two-Dimensional Matching Filtering[J]. Journal of Jilin University (Earth Science Edition), 2017, 47(1): 224-233. |
| [8] |
Herrmann F J, Urs B, Verschuur D J. Non-Linear Primary-Multiple Separation with Directional Curvelet Frames[J]. Geophysical Journal of the Royal Astronomical Society, 2007, 170(2): 781-799. DOI:10.1111/j.1365-246X.2007.03360.x |
| [9] |
Herrmann F J, Wang D L, Hennenfent G. Multiple Prediction from Incomplete Data with the Focused Curvelet Transform[J]. Society of Exploration Geophysicists, 2007(1): 2505. |
| [10] |
Wang D, Saab R, Yilmaz O, et al. Bayesian Wavefield Separation by Transform-Domain Sparsity Promotion[J]. Geophysics, 2008, 73(5): A33-A38. DOI:10.1190/1.2952571 |
| [11] |
王德利, 党丹, 刘伟明, 等. CFP技术层间多次波预测及Curvelet域相减方法[J]. 吉林大学学报(地球科学版), 2011, 41(3): 907-914. Wang Deli, Dang Dan, Liu Weiming, et al. CFP Technology Internal Multiple Prediction and Curvelet Domain Subtraction Method[J]. Journal of Jilin University (Earth Science Edition), 2011, 41(3): 907-914. |
| [12] |
王通, 王德利, 冯飞, 等. 三维稀疏反演多次波预测及曲波域匹配相减技术[J]. 吉林大学学报(地球科学版), 2017, 47(6): 1865-1874. Wang Tong, Wang Deli, Feng Fei, et al. Three-Dimensional Sparse Inversion Multiple Prediction and Curvelet Domain Matching and Subtraction Technology[J]. Journal of Jilin University (Earth Science Edition), 2017, 47(6): 1865-1874. |
| [13] |
刘成明, 王德利. 基于贝叶斯理论的Shearlet域一次波与多次波分离[J]. 石油学报, 2016, 37(4): 483-489. Liu Chengming, Wang Deli. Separation of Primary and Multiples in Shearlet Domain Based on Bayesian Theory[J]. Acta Petrolei Sinica, 2016, 37(4): 483-489. |
| [14] |
Markovsky I. Low Rank Approximation: Algorithms, Implementation, Applications[M]. Berlin: Springer Publishing Company, Incorporated, 2011.
|
| [15] |
Chen Y K, Bai M, Guan Z, et al. Five-Dimensional Seismic Data Reconstruction Using the Optimally Damped Rank-Reduction Method[J]. Geophysical Journal International, 2019, 218(1): 1. DOI:10.1093/gji/ggz113 |
| [16] |
Gao J, Stanton A, Sacchi M. Parallel Matrix Factorization Algorithm and Its Application to 5D Seismic Reconstruction and Denoising[J]. Geophysics, 2015, 80(6): V173-V187. DOI:10.1190/geo2014-0594.1 |
| [17] |
Hu B, Wang D L, Zhang L, et al. Structural Analysis of Lunar Regolith from LPR CH-2 Data Based on Adaptive f-x E MD: LPR Data[J]. Advances in Astronomy, 2019(1): 1528-1542. |
| [18] |
Chen Y, Zhang D, Jin Z, et al. Simultaneous Denoising and Reconstruction of 5D Seismic Data via Damped Rank-Reduction Method[J]. Geophysical Journal International, 2016, 206(3): 1695-1717. DOI:10.1093/gji/ggw230 |
| [19] |
Bai M, Wu J, Zu S, et al. A Structural Rank Reduction Operator for Removing Artifacts in Least-Squares Reverse Time Migration[J]. Computers and Geosciences, 2018, 117(8): 9-20. |
| [20] |
Huang W, Wang R, Chen Y, et al. Damped Multichannel Singular Spectrum Analysis for 3D Random Noise Attenuation[J]. Geophysics, 2016, 81(4): V261-V270. DOI:10.1190/geo2015-0264.1 |
| [21] |
Zou X, Ma Y, Qin Z. Fengyun-3B Microwave Humidity Sounder (MWHS) Data Noise Characterization and Filtering Using Principle Component Analysis[J]. IEEE Transactions on Geoscience & Remote Sensing, 2012, 50(12): 4892-4902. |
| [22] |
Cai J F, Candès E J, Shen Z. A Singular Value Thresholding Algorithm for Matrix Completion[J]. Siam Journal on Optimization, 2010, 20(4): 1956-1982. DOI:10.1137/080738970 |
| [23] |
Horn R A, Johnson C R. Matrix Analysis: 矩阵分析[M]. 北京: 人民邮电出版社, 2015. Horn R A, Johnson C R. Matrix Analysis[M]. Beijing: Posts & Telecom Press, 2015. |
| [24] |
Huang N E, Shen Z, Long S R, et al. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis[J]. Proceedings A, 1998, 454: 903-995. |
| [25] |
Chen Y, Zhou Y, Chen W, et al. Empirical Low-Rank Approximation for Seismic Noise Attenuation[J]. IEEE Transactions on Geoscience & Remote Sensing, 2017, 55(8): 1-16. |
| [26] |
石颖, 刘洪, 邹振. 基于波动方程表面多次波预测与自适应相减方法研究[J]. 地球物理学报, 2010, 53(7): 1716-1724. Shi Ying, Liu Hong, Zou Zhen. Surface-Related Multiples Prediction Based on Wave Equation and Adaptive Subtraction Investigation[J]. Chinese Journal of Geophysics, 2010, 53(7): 1716-1724. DOI:10.3969/j.issn.0001-5733.2010.07.023 |


