0 引言
随着科学技术水平的提高,地震勘探领域蓬勃发展。为了满足国内外油气需求,地震勘探逐渐向地表条件和地质构造复杂的地区展开,勘探深度随之增大,勘探环境变得极其恶劣,与此同时也伴随着复杂的噪声[1]。为了提高地震勘探数据的解释精度,如何压制噪声、提高信噪比成为了众多学者的研究热点。
地震数据通常含有各种类型的噪声。噪声来自信号收集环境、设备(电流噪声)、微震等[2]。噪声降低了地震记录的信噪比和分辨率,影响了地震处理和地层解释的精确性。传统随机噪声压制根据有效信号和噪声在视速度和频率等上的区别对噪声进行压制,如:f-k反褶积[3]、Radon变换[4]、径向道变换[5-6]、时频峰值滤波(TFPF)[7-8]、经验模态分解(EMD)[9-10]、矢量中值滤波[11-12]等方法。在20世纪80年代,小波变换是地震数据处理的重要方法[13],能够近乎完美地处理一维信号的奇点问题,但是它在一维信号上的优点却不能简单地推导至多维。许多可以多尺度几何分析二维甚至更高维度数据的算法不断出现,突破了小波变换的这一限制,比如:Wedgelet变换[14]、Bandelet变换[15]等自适应多尺度几何分析方法;Ridgelet变换[16]、Curvelet变换[17-18]、Contourlet变换[19-20]等非自适应多尺度几何分析方法。目前,多尺度几何分析方法已经在地震数据处理领域得到了广泛运用。
G. Easley、K. Guo和D. Labate等[21-23]提出了一种更有效的二维图像表示方法——Shearlet变换。Shearlet变换集成了Contourlet变换和Curvelet变换的优点,具有很好的局部化特征、抛物线型的尺度化特性、高度的方向敏感性、接近最优的稀疏表示性能,因此Shearlet变换可以完美地表征二维信号的全部奇异点,并自适应地追踪奇异曲线的方向。由于Shearlet变换具有这些优良特点,并且选择合适的阈值进行去噪就能获得比小波变换和其他变换域去噪方法更好的效果,Shearlet变换已成功应用于较多领域。
Kong等[24]提出Shearlet变换和全变差正则化相结合的去噪方法;Hosseini等[25]利用Shearlet变换对地震数据进行多次波分离;董新桐等[26]提出基于高阶加权阈值函数的Shearlet变换处理丘陵地带地震数据噪声,提高信噪比并保留信号幅度;李民等[27]对地震信号进行非下采样Shearlet变换,对Shearlet系数进行主成分分析并采用非局部均值处理,在低噪声情况下能够获得优于非局部均值算法的去噪效果;李娟等[28]通过Shearlet变换获取了微地震记录各个尺度与方向上的Shearlet域系数,并叠加有效信号集中方向的系数,让信号和噪声间产生差异,最后通过峰度特征实现初至波拾取;刘成明等[29]结合压缩感知和Shearlet变换,建立了稀疏约束地震数据的重建方法;郑升等[30]通过卷积神经网络学习沙漠地震信号与随机噪声Shearlet域系数间的关系,利用此映射关系间接地获得有效信号系数,最后通过Shearlet逆变换恢复有效信号。
Shearlet变换是一类全新的多尺度几何分析工具,适用于具有丰富纹理、轮廓和边缘等方向性信息的地震数据。与其他去噪方法相比,Shearlet在地震数据随机噪声压制方面具有很大优势。但传统Shearle全局阈值主要利用地震数据在Shearlet域的稀疏性对噪声进行压制,而忽略了有效信号和随机噪声在Shearlet域不同尺度和方向上的分布特性。有效信号在低尺度下分布较多,随着尺度的增加,有效信号不断减少,随机噪声逐渐占据主导地位,而各尺度下的有效信号分布与方向有关,与基函数方向一致的有效信号Shearlet系数大,反之则小。所以固定的全局阈值显然无法适应Shearlet变换的尺度性和方向性,在去除噪声的同时会损失大量有效信号。
针对传统Shearlet全局阈值不能随尺度和方向变化的问题,本文对含噪理论数据进行Shearlet变换,根据有效信号在不同尺度下的分布规律,进而计算各尺度下不同方向Shearlet系数的L2范数,并对其进行数据重排,分析各尺度下有效信号的分布特点;总结规律,提出随尺度和方向变化的Shearlet域自适应阈值去噪方法,达到最大限度去除随机噪声、保留有效信号的目的;通过对理论地震记录和实际地震数据的处理,证明Shearlet变换自适应阈值算法对地震数据随机噪声压制的有效性与适用性。
1 Shearlet变换算法原理Shearlet变换由拉普拉斯金字塔变换和方向滤波器组构成。当维数n=2时,设尺度矩阵和剪切矩阵分别为:
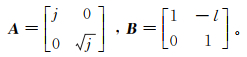 (1)
(1) 式中:A是尺度矩阵,可以划分尺度;j>0,是尺度参数;B是剪切矩阵,可以剖分方向;l是剪切参数。具有合成膨胀的仿射系统定义为
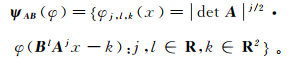 (2)
(2) 式中:φ∈L2(R2),为剪切波函数,L表示可积空间;x为待处理数据;det(·)为取行列式;k为平移参数。
如果ψAB(φ)满足Parseval框架(紧框架),即对于任意函数f∈L2(R2)满足
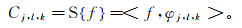 (3)
(3) 式中:Cj, l, k为Shearlet域系数;S为Shearlet正变换;<· >为求内积。那么ψAB(φ)被称为合成小波。参量j、l、k可以控制各方向与尺度的剖分,通过不同尺度方向位置的基函数φj, l, k与函数f求内积,可得到对应尺度方向位置的Shearlet域系数Cj, l, k(式(3)),这个过程实际上是用平移、伸缩与旋转过后的基函数来逼近信号。
另外,当任意Shearlet元素ζ=(ζ1,ζ2)∈Ȓ2,Ȓ2为频域空间,使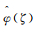
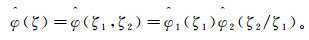 (4)
(4) 式中: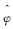
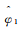
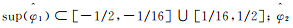
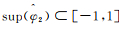
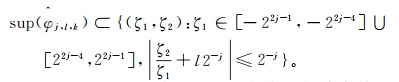 (5)
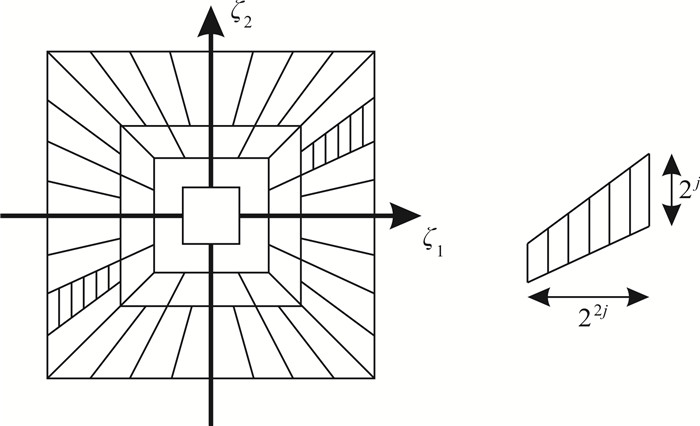
(5) 图 1展示了连续Shearlet变换的频域支撑区间,任意Shearlet元素的频域支撑都呈现梯形状,大小近似为22j·2j,沿着斜率为l2-j的直线分布。
|
| 图 1 频域剖分与其支撑区间 Fig. 1 Frequency domain subdivision and its support interval |
|
|
Shearlet变换能多尺度分析描述高维信号的几何奇异性,具有高度的方向敏感性,其频域支撑是各向异性的,而地震记录的细节信息代表各向异性的几何特征,于是Shearlet变换可以通过最少的稀疏系数逼近奇异曲线,完成对地震记录的稀疏表示。对于变换域的随机噪声压制方法,母函数对有效信号稀疏表示能力越高,去噪效果越好。
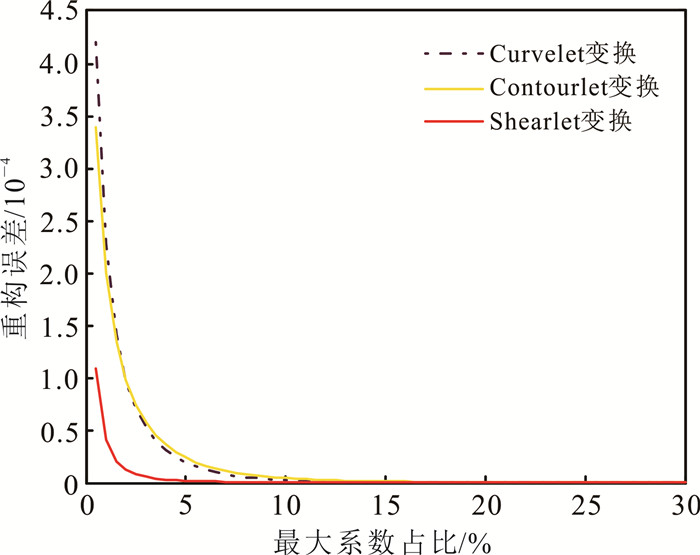
本文利用Curvelet变换、Contourlet变换和Shearlet变换分解不含噪声的地震数据,将分解后的变换域系数按大小顺序排列,通过保留不同比例的变换域系数进行稀疏重构,计算稀疏重构的结果与原始数据的误差,越小的重构误差代表越好的稀疏表示能力。
如图 2所示,当保留4%的最大系数时,Shearlet变换的重构误差已近乎为0,此时Curvelet变换和Contourlet变换仍与原始数据有一定的误差,直到保留的最大系数比例达到10%时,重构误差才近乎为0。对比可知,Shearlet变换对地震数据具有更好的稀疏表示能力。
|
| 图 2 变换域系数重构误差对比 Fig. 2 Transformation domain coefficient reconstruction error comparison |
|
|
地震数据经Shearlet分解过后可以获得随尺度与方向变化的Shearlet域系数。当有效信号与Shearlet基函数方向差不多时,其系数较大;而当有效信号与基函数方向不一致时,其系数较小。实际上,地震数据同相轴能量比随机噪声强许多。根据这个规律设置适当阈值,通过阈值化处理舍弃低于阈值的系数,再利用Shearlet逆变换就得到了压制随机噪声的地震数据。
2.1 自适应阈值函数变换域去噪算法阈值选取与阈值函数对随机噪声压制效果影响大。Shearlet全局阈值对所有Shearlet域系数使用一个固定不变的阈值,而各尺度与方向上的有效信号以及随机噪声普遍具有差异,因此全局阈值很难在去除随机噪声的同时很好地保护有效信号。
传统阈值函数对Shearlet系数的阈值化处理过程可以概括为
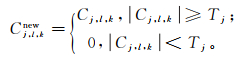 (6)
(6) 式中:Cj, l, knew为经阈值函数保留的系数;Tj为全局阈值。
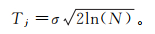 (7)
(7) 式中:σ为噪声的标准差;N为地震数据的总采样点数。
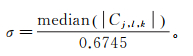 (8)
(8) 式中,median为取中值。
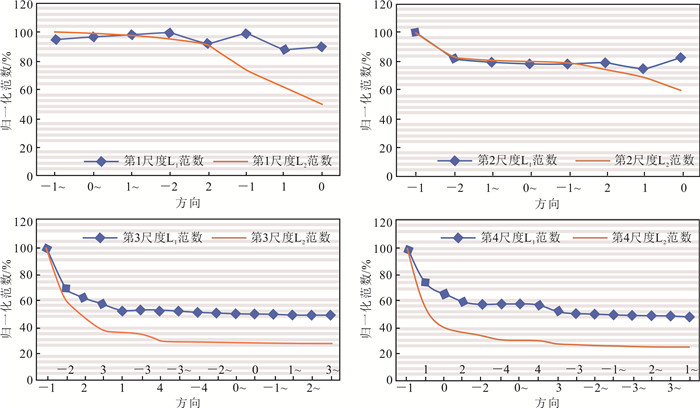
为了刻画地震数据在Shearlet分解之后各尺度及方向上有效信号和随机噪声的分布特性,自适应选取阈值,笔者对一组含噪理论数据经Shearlet变换后的Shaerlet系数进行了统计,分解尺度为4,方向矩阵为[1 1 2 2],包含水平锥尺度1、2各5个方向,尺度3、4各9个方向;垂直锥尺度1、2各3个方向,尺度3、4各7个方向,为区别表示,在图 3、4中方向后添加“~”表示垂直锥方向;水平锥与垂直锥共计48个方向。
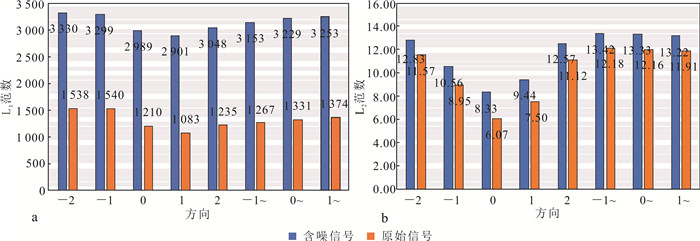
|
| 图 3 尺度1加噪前后各方向Shearlet系数重排序后的L1(a)、L2(b)范数变化趋势 Fig. 3 Norm variation trend of L1 (a) and L2 (b) after Shearlet coefficients in all directions reordered before and after noise was added at scale 1 |
|
|
|
| 图 4 不同尺度下各方向Shearlet系数归一化重排序后的L1、L2范数变化趋势 Fig. 4 Variation trend of L1 and L2 norm after Shearlet coefficients are normalized and reordered in different directions at different scales |
|
|
作者计算了原始信号及含噪信号在尺度1上的L1和L2范数。如图 3所示,发现加噪前后L1范数变化极大,噪声的加入平滑了L1范数的变化趋势;而L2范数在加噪前后变化不大,且L2范数在不同方向上的变化趋势明显。对每个尺度进行归一化重排序后发现,各尺度下Shearlet系数的L2范数按不同方向近似规律排列,L2范数随方向变化不断减小,并且L2范数变化趋势比L1更为明显,能更为敏感地刻画有效信号在不同方向上的分布变化规律(图 4)。实际上,有效信号的相对数值远大于随机噪声,因此Shearlet系数的L2范数越大代表该方向上的有效信号越多,反之代表此方向上随机噪声越多。这也意味着可以用Shearlet系数的L2范数来表征各尺度与方向上有效信号和随机噪声之间的相关性。因此,本文选择L2范数构建阈值。
Shearlet域系数的L2范数为
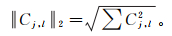 (9)
(9) 式中,‖ Cj, l‖2为j尺度l方向Shearlet系数的L2范数。
本文在Shearlet全局阈值基础上提出随尺度方向变化而变化的自适应阈值,其表达式如下:
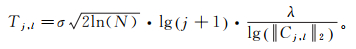 (10)
(10) 式中,λ为常数。随着尺度增加,有效信号减少,lg(j+1)逐渐增大,采取较大的阈值压制噪声信号。对于任一固定尺度,某一方向上Shearlet系数的L2范数越大,则在此方向有效信号越多,λ/lg(‖Cj, l ‖2)越小,故在此方向上可以采用较小的阈值保护有效信号;反之采用较大的阈值来去除随机噪声。本文阈值方法在尽可能压制随机噪声的同时也很好地保护了有效信号。
2.2 噪声压制评价指标本文使用峰值信噪比、信噪比、均方差来评价去噪效果。峰值信噪比和信噪比越大,噪声压制效果越好;均方差越小,去噪结果更加贴近原始数据。
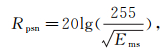 (11)
(11) 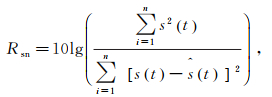 (12)
(12) 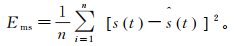 (13)
(13) 式中:Rpsn为峰值信噪比;Rsn为信噪比;Ems为均方差;s(t)为去噪后的结果;ŝ(t)为原始有效信号。
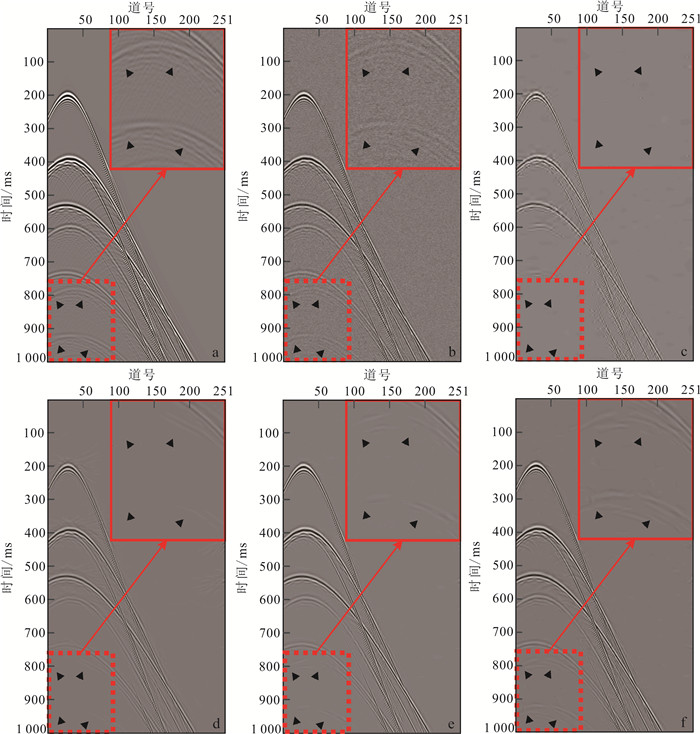
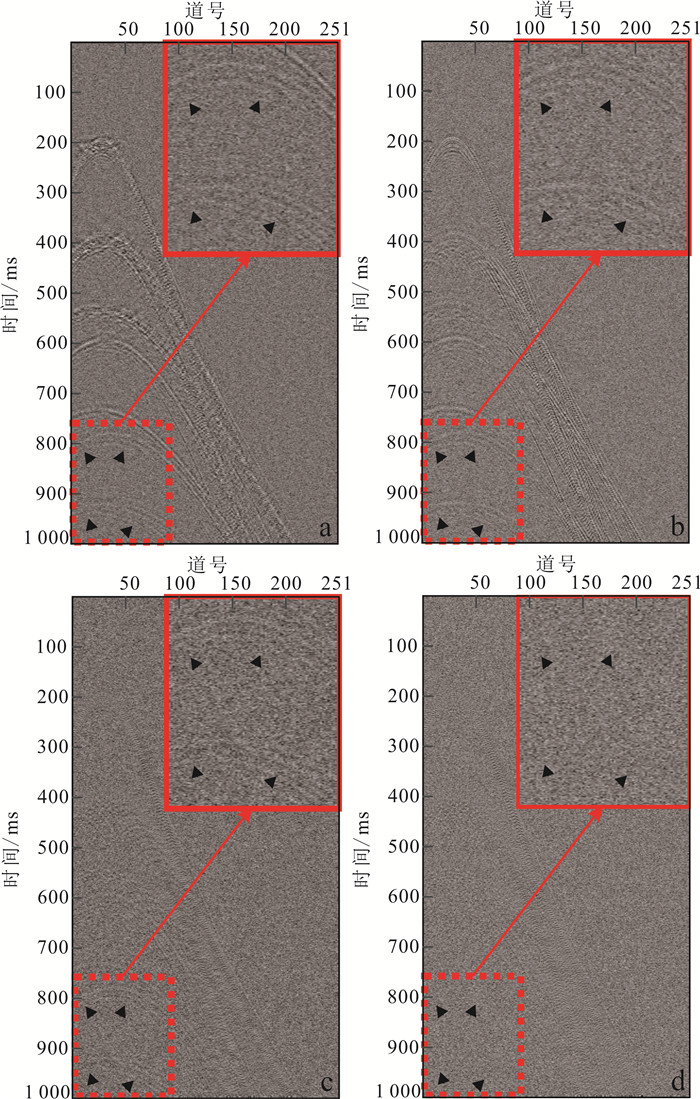
3 理论数据与实际数据应用 3.1 理论数据仿真为了验证自适应阈值的有效性,本文对理论地震记录进行测试。Shearlet变换选择正交小波作为母函数,分解尺度为4,方向矩阵为[1 1 2 2]。理论地震记录如图 5a所示,待测试地震数据含251道,每道含有1 000个采样点,间隔1 ms采样。对合成地震记录添加若干随机噪声,如图 5b所示,其中的深层同相轴含能量较弱的有效信号被噪声覆盖,给地震数据的后续处理带来了干扰。图 5c、d、e、f分别展示了小波变换、曲波变换、Shearlet全局阈值去噪、Shearlet自适应阈值去噪效果,右上角放大显示了深层同向轴区域,结果显示小波变换、曲波变换、Shearlet全局阈值虽然压制了大部分的随机噪声,但仍有部分残留的噪声,深部同向轴也未能很好地从噪声中恢复,压制噪声的同时丢失了许多较弱的有效信号。从差剖面(图 6)可以看出,这3种方法在去噪的同时也损失了大量的有效信号,深部同向轴无法识别,降低了信噪比,影响后续地震数据的处理,为地震数据的可读性和后期处理带来干扰。与小波变换、曲波变换、Shearlet全局阈值相比,本文方法不仅很好地压制了随机噪声,也很大程度上恢复了深层同向轴,增强连续性,提高了地震记录的信噪比(图 5f),且Shearlet自适应阈值的差剖面含较少的有效信号(图 6d)。
|
| a. 理论地震记录;b. 含噪地震记录;c. 小波变换;d. 曲波变换;e. Shearlet全局阈值去噪;f. Shearlet自适应阈值去噪。 图 5 理论地震记录去噪效果对比 Fig. 5 Comparison of theoretical seismic record denoising effect |
|
|
|
| a. 小波变换;b. 曲波变换;c. Shearlet全局阈值去噪;d. Shearlet自适应阈值去噪。 图 6 不同去噪方法对应的理论地震记录差剖面 Fig. 6 Theoretical seismic record difference profiles corresponding to different denoising methods |
|
|
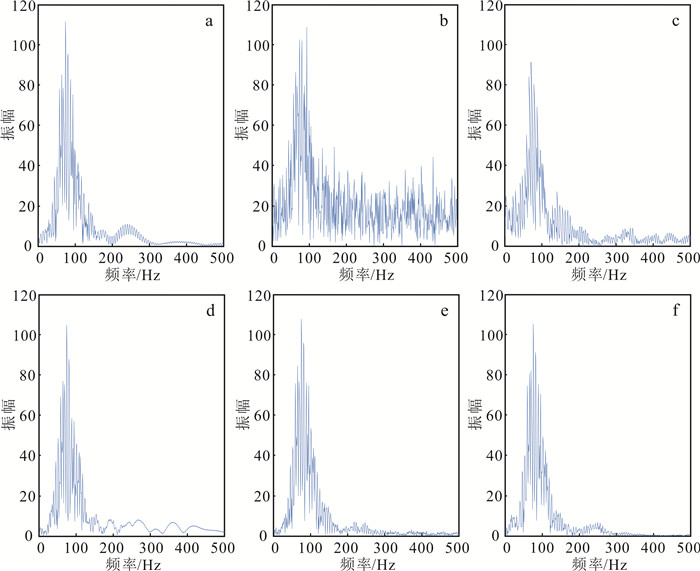
分别抽取原始信号、含噪信号、小波变换、曲波变换、Shearlet全局阈值和自适应阈值去噪信号的第75道,通过频谱分析来说明自适应阈值比全局阈值的优越之处。对比图 7中的原始信号(图 7a)和含噪信号(图 7b)的频谱可知,随机噪声在地震数据中主要以高频形式呈现。从图 7c、d、e、f可以看出,4种方法都能不同程度地压制随机噪声,但小波变换和曲波变换残留噪声较多,Shearlet自适应阈值高频残留噪声比全局阈值更低,且波形较之更与原始信号相符,说明Shearlet自适应阈值能很好地压制随机噪声,保留有效信号。
|
| a. 原始信号;b. 含噪信号;c. 小波变换;d. 曲波变换;e. Shearlet全局阈值去噪;f. Shearlet自适应阈值去噪。 图 7 各方法频谱对比 Fig. 7 Spectrum comparison of various methods |
|
|
表 1展示了含噪地震数据、小波变换、曲波变换、Shearlet全局阈值与自适应阈值去噪结果的峰值信噪比、信噪比与均方差。加入随机噪声的模拟地震记录信噪比为0.929 9 dB,对比其他3种方法,Shearlet自适应阈值的信噪比提升更为明显,去噪后的信噪比达到了11.565 1 dB,与Shearlet全局阈值对比,提升了0.550 7 dB。Shearlet自适应阈值在压制噪声的同时具有更低的均方差,代表去噪后的结果与原始不含噪地震数据最为接近。进一步说明了本文提出方法对地震噪声具有更强的压制能力,去噪结果与原始信号偏差较小,能很好地保护弱信号。
| 峰值信噪比/dB | 信噪比/dB | 均方差 | |
| 含噪地震数据 | 53.015 0 | 0.929 9 | 0.129 60 |
| 小波变换 | 58.772 4 | 6.689 3 | 0.086 27 |
| 曲波变换 | 58.353 2 | 6.270 1 | 0.095 00 |
| Shearlet全局阈值去噪 | 63.097 5 | 11.014 4 | 0.031 87 |
| Shearlet自适应阈值去噪 | 63.596 7 | 11.565 1 | 0.028 07 |
将Shearlet自适应阈值去噪方法应用于实际地震记录,以此进一步验证其有效性。图 8a为某地区实际地震记录的叠后剖面,其中包含了一个褶皱构造。由于复杂的采集环境,图中含有非常多的随机噪声,同相轴不连续,边界清晰度低,部分能量不强的有效信息淹没在随机噪声里,给地震记录的信噪比和分辨率带来了影响,无法精准判断和识别其中包含的地质信息。

|
| a. 含噪信号;b. 小波变换;c. 曲波变换;d. Shearlet全局阈值去噪;e. Shearlet自适应阈值去噪。 图 8 实际地震记录去噪效果对比 Fig. 8 Comparison of actual seismic record denoising effect |
|
|
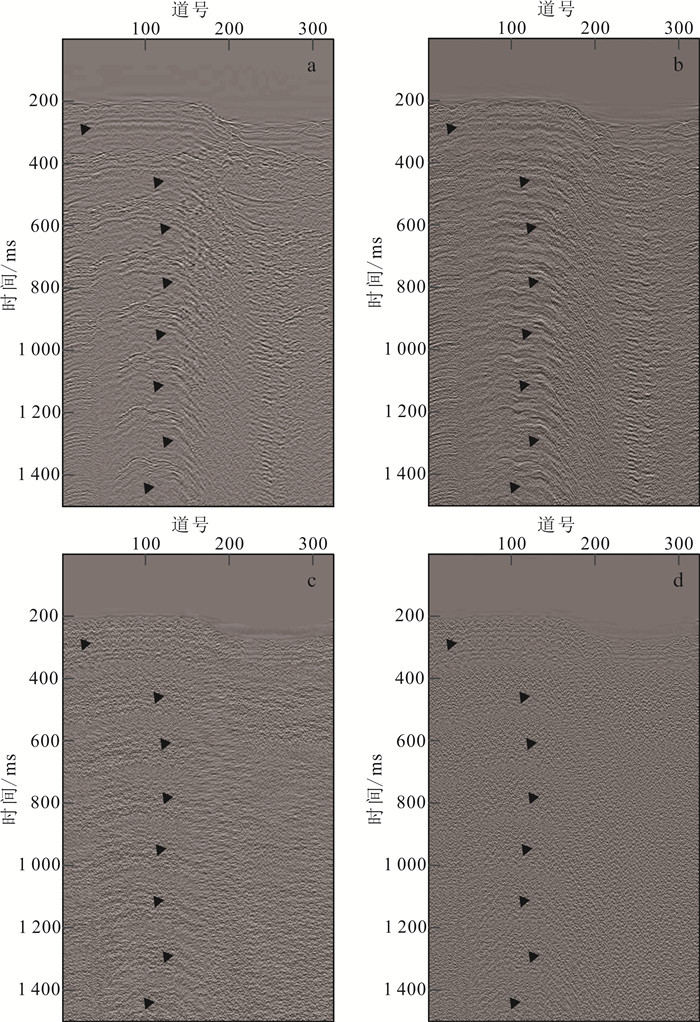
分别使用小波变换、曲波变换、Shearlet全局阈值和自适应阈值对此实际地震记录进行去噪处理。由图 8b、c、d可以看出,与原始地震记录相比,小波变换、曲波变换、Shearlet全局阈值的去噪结果随机噪声得到了一定程度的去除,但同向轴的连续性一般,部分能量较弱的有效信号未能有所改善。如图 8e所示,Shearlet自适应阈值的去噪结果明显优于前3种方法,随机噪声得到了有效的去除,同向轴变得更加连续,边界也更为清晰,部分能量较弱的有效信号也顺利从随机噪声里恢复,增强了实际地震数据的信噪比,提高了分辨率。
图 9为不同方法去噪后对应的差剖面,可以看到:小波变换、曲波变换、Shearlet全局阈值的差剖面均含较多的有效信号,在去噪的同时也损失了大量的有效信号,导致深部同向轴难以识别,边界十分模糊;而Shearlet自适应阈值不仅很好地压制了随机噪声,也很大程度上恢复了深层同向轴,说明本文提出方法能很好地适用于实际地震数据处理。
|
| a. 小波变换;b. 曲波变换;c. Shearlet全局阈值去噪;d. Shearlet自适应阈值去噪。 图 9 不同方法去噪对应的实际地震记录差剖面 Fig. 9 Actual seismic record difference profiles corresponding to different denoising methods |
|
|
1) 本文分析含噪数据各尺度方向上Shearlet系数L2范数值的分布规律,利用L2范数值计算自适应阈值,解决了全局阈值不能随尺度、方向变化的问题。
2) 与L1范数值自适应阈值相比,L2范数值在不同方向上的变化趋势较L1范数更明显,且受噪声影响较小,能更为敏感地刻画有效信号在不同方向上的分布变化规律。
3) 根据模拟数据与实际地震记录去噪结果可知,自适应阈值在去除随机噪声的同时,能够很好地保护有效信号,增强同相轴连续性,有效地提高地震数据的信噪比和分辨率,对精准判断和识别地震数据中包含的地质信息具有重大意义。
| [1] |
刘阳, 赵虎, 尹成, 等. 起伏地表条件下的弹性波叠前逆时偏移[J]. 煤田地质与勘探, 2019, 47(1): 181-186. Liu Yang, Zhao Hu, Yin Cheng, et al. Elastic Wave Prestack Reverse Time Migration on Undulating Surface[J]. Coal Geology & Exploration, 2019, 47(1): 181-186. DOI:10.3969/j.issn.1001-1986.2019.01.028 |
| [2] |
张军华. 地震资料去噪方法: 原理、算法、编程及应用[M]. 青岛: 石油大学出版社, 2011. Zhang Junhua. Seismic Data Denoising Method: Principle Algorithm Programming and Application[M]. Qingdao: China University of Petroleum Press, 2011. |
| [3] |
万光南. f-k滤波在压制面波噪声中的应用[J]. 中州煤炭, 2014(2): 99-101. Wan Guangnan. Application off-k Filtering in Noise Suppression of Surface Wave[J]. Zhongzhou Coal, 2014(2): 99-101. DOI:10.3969/j.issn.1003-0506.2014.02.036 |
| [4] |
贾春梅, 姜国庆, 刘志成, 等. 频域稀疏双曲Radon变换去噪方法[J]. 物探与化探, 2016, 40(3): 527-533. Jia Chunmei, Jiang Guoqing, Liu Zhicheng, et al. Denoising Method Based on Sparse Hyperbolic Radon Transform in the Frequency Domain[J]. Geophysical and Geochemical Exploration, 2016, 40(3): 527-533. |
| [5] |
曹善舒, 李月, 吴宁. 自适应径向道TFPF压制地震记录随机噪声[J]. 吉林大学学报(信息科学版), 2016, 34(2): 10-17. Cao Shanshu, Li Yue, Wu Ning. Self-Adaptive Radial-Trace TFPF for Seismic Random Noise Attenuation[J]. Journal of Jilin University (Information Science Edition), 2016, 34(2): 10-17. |
| [6] |
张洁, 李月. 平行径向道时频峰值滤波消减地震资料的随机噪声[J]. 吉林大学学报(工学版), 2014, 44(3): 882-887. Zhang Jie, Li Yue. Reduction of Random Noise in Seismic Data by Parallel Radial-Trace Time-Frequency Peek Filtering[J]. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(3): 882-887. |
| [7] |
Li J, Meng K, Yuan L, et al. Adaptive Linear TFPF for Seismic Random Noise Attenuation[J]. Journal of Petroleum Exploration & Production Technology, 2018, 8(4): 1-11. DOI:10.1007/s13202-018-0429-4 |
| [8] |
Zhuang G, Yue L, Liu Y, et al. Varying-Window-Length TFPF in High-Resolution Radon Domain for Seismic Random Noise Attenuation[J]. IEEE Geoscience & Remote Sensing Letters, 2014, 12(2): 404-408. |
| [9] |
刘霞, 黄阳, 黄敬, 等. 基于经验模态分解(EMD)的小波熵阈值地震信号去噪[J]. 吉林大学学报(地球科学版), 2016, 46(1): 262-269. Liu Xia, Huang Yang, Huang Jing, et al. Wavelet Entropy Threshold Seismic Signal Denoising Based on Empirical Mode Decomposition (EMD)[J]. Journal of Jilin University (Earth Science Edition), 2016, 46(1): 262-269. |
| [10] |
杨凯, 刘伟. 基于改进EMD的地震信号去噪[J]. 西南石油大学学报, 2012, 34(4): 75-82. Yang Kai, Liu Wei. Random Noise Attenuation of Seismic Signal Based on Improved EMD[J]. Journal of Southwest Petroleum University, 2012, 34(4): 75-82. DOI:10.3863/j.issn.1674-5086.2012.04.010 |
| [11] |
孙哲, 王建锋, 王静, 等. 基于时空变中值滤波的随机噪声压制方法[J]. 石油地球物理勘探, 2016, 51(6): 1094-1102. Sun Zhe, Wang Jianfeng, Wang Jing, et al. Random Noise Elimination Based on the Time-Spacevariant Median Filtering[J]. Oil Geophysical Prospecting, 2016, 51(6): 1094-1102. |
| [12] |
王伟, 高静怀, 陈文超, 等. 基于结构自适应中值滤波器的随机噪声衰减方法[J]. 地球物理学报, 2012, 55(5): 1732-1741. Wang Wei, Gao Jinghuai, Chen Wenchao, et al. Random Seismic Noise Suppression via Structure-Adaptive Median Filter[J]. Chinese Journal of Geophysics, 2012, 55(5): 1732-1741. |
| [13] |
Kourouniotis F P, Kubichek R F, Boyd N G, et al. Application of the Wavelet Transform in Seismic Data Processing for the Development of New Noise Reduction Techniques[J]. Proc.SPIE-Wavelet Applications in Signal and Image Processing IV, 1996, 2825: 620-631. |
| [14] |
Donoho D L. Wedgelets: Nearly Minimax Estimation of Edges[J]. Annals of Statistics, 1999, 27(3): 859-897. |
| [15] |
Pennec E L, Mallat S. Sparse Geometric Image Representations with Bandelets[J]. IEEE Transactions on Image Processing, 2005, 14(4): 423-438. DOI:10.1109/TIP.2005.843753 |
| [16] |
Do M N, Vetterli M. The Finite Ridgelet Transform for Image Representation[J]. IEEE Transactions on Image Processing, 2003, 12(1): 16-28. DOI:10.1109/TIP.2002.806252 |
| [17] |
Starck J L, Candes E J, Donoho D L. The Curvelet Transform for Image Denoising[J]. IEEE Transactions on Image Processing, 2002, 11(6): 670-684. DOI:10.1109/TIP.2002.1014998 |
| [18] |
张华, 陈小宏, 李红星, 等. 曲波变换三维地震数据去噪技术[J]. 石油地球物理勘探, 2017, 52(2): 226-232. Zhang Hua, Chen Xiaohong, Li Hongxing, et al. 3D Seismic Data De-Noising Approach Based on Curve-Let Transform[J]. Oil Geophysical Prospecting, 2017, 52(2): 226-232. |
| [19] |
Do M N, Vetterli M. The Contourlet Transform: An Efficient Directional Multiresolution Image Representation[J]. IEEE Transactions on Image Processing: A Publication of the IEEE Signal Processing Society, 2005, 14(12): 2091-2106. DOI:10.1109/TIP.2005.859376 |
| [20] |
王建花, 王守东, 刘燕峰. 基于Contourlet系数相关性的地震噪声压制方法[J]. 中国海上油气, 2016, 28(1): 39-44. Wang Jianhua, Wang Shoudong, Liu Yanfeng. Seismic Noise Suppression Method Based on Correlation of Contourlet Coefficients[J]. China Offshore Oil and Gas, 2016, 28(1): 39-44. |
| [21] |
Easley G, Labate D, Lim W Q. Sparse Directional Image Representations Using the Discrete Shearlet Transform[J]. Applied & Computational Harmonic Analysis, 2008, 25(1): 25-46. |
| [22] |
Guo K, Labate D, Lim W Q, et al. Wavelets with Composite Dilations and Their MRA Properties[J]. Applied & Computational Harmonic Analysis, 2006, 20(2): 202-236. |
| [23] |
Labate D, Guo K. Optimally Sparse Multidimensional Representation Using Shearlets[J]. SIAM Journal on Mathematical Analysis, 2007, 39(1): 298-318. |
| [24] |
Kong D, Peng Z. Seismic Random Noise Attenuation Using Shearlet and Total Generalized Variation[J]. Journal of Geophysics & Engineering, 2015, 12(6): 1024-1035. |
| [25] |
Hosseini S A, Javaherian A, Hassani H, et al. Adaptive Attenuation of Aliased Ground Roll Using the Shearlet Transform[J]. Journal of Applied Geophysics, 2015, 112: 190-205. DOI:10.1016/j.jappgeo.2014.11.018 |
| [26] |
董新桐, 马海涛, 李月. 丘陵地带地震资料随机噪声压制新技术: 高阶加权阈值函数的Shearlet变换[J]. 地球物理学报, 2019, 62(10): 4039-4046. Dong Xintong, Ma Haitao, Li Yue. The New Technology for Suppression of Hilly Land Seismic Random Noise: Shearlet Transform and the High Order Weighted Threshold Function[J]. Chinese Journal of Geophysics, 2019, 62(10): 4039-4046. DOI:10.6038/cjg2019M0582 |
| [27] |
李民, 周亚同, 李梦瑶, 等. Shearlet域基于非局部均值的地震信号去噪[J/OL]. 重庆大学学报. [2016-12-30]. http://kns.cnki.net/kcms/detail/50.1044.n.20191227.1804.011.html. Li Min, Zhou Yatong, Li Mengyao, et al. Denoising of Seismic Signals Based on Non-Local Mean in Shearlet Domain[J/OL]. Journal of Chongqing University. [2016-12-30]. http://kns.cnki.net/kcms/detail/50.1044.n.20191227.1804.011.html. |
| [28] |
李娟, 计硕, 李月, 等. 基于Shearlet变换和峰度特性的井中微地震初至波拾取[J]. 吉林大学学报(工学版), 2019, 49(1): 290-295. Li Juan, Ji Shuo, Li Yue, et al. First Arrival Pickup of Downhole Microseismic Signal Based on Shearlet Transform and Kurtosis Characteristic[J]. Journal of Jilin University (Engineering and Technology Edition), 2019, 49(1): 290-295. |
| [29] |
刘成明, 王德利, 胡斌, 等. Shearlet域稀疏约束地震数据重建[J]. 吉林大学学报(地球科学版), 2016, 46(6): 1855-1864. Liu Chengming, Wang Deli, Hu Bin, et al. Seismic Data Interpolation Based on Sparse Constraint in Shearlet Domain[J]. Journal of Jilin University (Earth Science Edition), 2016, 46(6): 1855-1864. |
| [30] |
郑升, 李月, 董新桐. Shearlet域深度残差CNN用于沙漠地震信号去噪[J]. 吉林大学学报(信息科学版), 2019, 37(1): 1-7. Zheng Sheng, Li Yue, Dong Xintong. Shearlet Domain Deep Residual CNN for Removing Noise from Desert Seismic Signals[J]. Journal of Jilin University (Information Science Edition), 2019, 37(1): 1-7. DOI:10.3969/j.issn.1671-5896.2019.01.001 |


